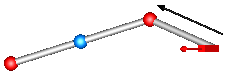
The joints in this package are mainly designed to be used in kinematic loop structures. Every component consists of 3 elementary joints. These joints are combined in such a way that the kinematics of the 3 joints between frame_a and frame_b are computed from the movement of frame_a and frame_b, i.e., there are no constraints between frame_a and frame_b. This requires to solve a non-linear system of equations which is performed analytically (i.e., when a mathematical solution exists, it is computed efficiently and reliably). A detailed description how to use these joints is provided in MultiBody.UsersGuide.Tutorial.LoopStructures.AnalyticLoopHandling.
The assembly joints in this package are named JointXYZ where XYZ are the first letters of the elementary joints used in the component, in particular:
| P | Prismatic joint |
| R | Revolute joint |
| S | Spherical joint |
| U | Universal joint |
For example, JointUSR is an assembly joint consisting of a universal, a spherical and a revolute joint.
This package contains the following models:
| Model | Description |
|---|---|
| JointUPS | Universal - prismatic - spherical joint aggregation
|
| JointUSR | Universal - spherical - revolute joint aggregation
|
| JointUSP | Universal - spherical - prismatic joint aggregation
|
| JointSSR | Spherical - spherical - revolute joint aggregation
with an optional mass point at the rod connecting
the two spherical joints
|
| JointSSP | Spherical - spherical - prismatic joint aggregation
with an optional mass point at the rod connecting
the two spherical joints
|
| JointRRR | Revolute - revolute - revolute joint aggregation for planar loops
|
| JointRRP | Revolute - revolute - prismatic joint aggregation for planar loops
|
Note, no component of this package has potential states, since the components are designed in such a way that the generalized coordinates of the used elementary joints are computed from the frame_a and frame_b coordinates. Still, it is possible to use the components in a tree structure. In this case states are selected from bodies that are connected to the frame_a or frame_b side of the component. In most cases this gives a less efficient solution, as if elementary joints of package Modelica.Mechanics.MultiBody.Joints would be used directly.
The analytic handling of kinematic loops by using joint aggregations with 6 degrees of freedom as provided in this package, is a new methodology. It is based on a more general method for solving non-linear equations of kinematic loops developed by Woernle and Hiller. An automatic application of this more general method is difficult, and a manual application is only suited for specialists in this field. The method introduced here is a compromize: It can be quite easily applied by an end user, but for a smaller class of kinematic loops. The method of the "characteristic pair of joints" from Woernle and Hiller is described in:
Extends from Modelica.Icons.Package (Icon for standard packages).
| Name | Description |
|---|---|
| Universal - prismatic - spherical joint aggregation (no constraints, no potential states) | |
| Universal - spherical - revolute joint aggregation (no constraints, no potential states) | |
| Universal - spherical - prismatic joint aggregation (no constraints, no potential states) | |
| Spherical - spherical - revolute joint aggregation with mass (no constraints, no potential states) | |
| Spherical - spherical - prismatic joint aggregation with mass (no constraints, no potential states) | |
| Planar revolute - revolute - revolute joint aggregation (no constraints, no potential states) | |
| Planar revolute - revolute - prismatic joint aggregation (no constraints, no potential states) |
 Modelica.Mechanics.MultiBody.Joints.Assemblies.JointUPS
Modelica.Mechanics.MultiBody.Joints.Assemblies.JointUPS
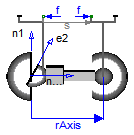
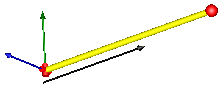
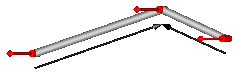
This component consists of a universal joint at frame_a, a spherical joint at frame_b and a prismatic joint along the line connecting the origin of frame_a and the origin of frame_b, see the default animation in the following figure (the axes vectors are not part of the default animation):

This joint aggregation has no mass and no inertia and introduces neither constraints nor potential state variables. It is especially useful to build up more complicated force elements where the mass and/or inertia of the force element shall be taken into account.
The universal joint is defined in the following way:
The definition of axis 2 of the universal joint is performed according to the most often occuring case. In a future release, axis 2 might be explicitly definable via a parameter. However, the treatment is much more complicated and the number of operations is considerably higher, if axis 2 is not orthogonal to axis 1 and to the connecting rod.
Note, there is a singularity when axis 1 and the connecting line are parallel to each other. Therefore, if possible n1_a should be selected in such a way that it is perpendicular to nAxis_ia in the initial configuration (i.e., the distance to the singularity is as large as possible).
An additional frame_ia is present. It is fixed on the line connecting the universal and the spherical joint at the origin of frame_a. The placement of frame_ia on this line is implicitly defined by the universal joint (frame_a and frame_ia coincide when the angles of the two revolute joints of the universal joint are zero) and by parameter vector nAxis_ia, an axis vector directed along the line from the origin of frame_a to the spherical joint, resolved in frame_ia.
An additional frame_ib is present. It is fixed in the line connecting the prismatic and the spherical joint at the origin of frame_b. It is always parallel to frame_ia.
Note, this joint aggregation can be used in cases where in reality a rod with spherical joints at each end are present. Such a system has an additional degree of freedom to rotate the rod along its axis. In practice this rotation is usually of no interested and is mathematically removed by replacing one of the spherical joints by a universal joint.
The easiest way to define the parameters of this joint is by moving the MultiBody system in a reference configuration where all frames of all components are parallel to each other (alternatively, at least frame_a, frame_ia and frame_ib of the JointUSP joint should be parallel to each other when defining an instance of this component).
Extends from Interfaces.PartialTwoFramesDoubleSize (Base model for components providing two frame connectors + outer world + assert to guarantee that the component is connected (default icon size is factor 2 larger as usual)).
| Type | Name | Default | Description |
|---|---|---|---|
| Boolean | animation | true | = true, if animation shall be enabled |
| Boolean | showUniversalAxes | true | = true, if universal joint shall be visualized with two cylinders, otherwise with a sphere (provided animation=true) |
| Axis | n1_a | {0,0,1} | Axis 1 of universal joint resolved in frame_a (axis 2 is orthogonal to axis 1 and to line from universal to spherical joint) [1] |
| Position | nAxis_ia[3] | {1,0,0} | Axis vector along line from origin of frame_a to origin of frame_b, resolved in frame_ia [m] |
| Position | s_offset | 0 | Relative distance offset (distance between frame_a and frame_b = s(t) + s_offset) [m] |
| Animation | |||
| if animation = true | |||
| Diameter | sphereDiameter | world.defaultJointLength | Diameter of spheres representing the spherical joints [m] |
| Color | sphereColor | Modelica.Mechanics.MultiBody... | Color of spheres representing the spherical joints |
| Diameter | axisDiameter | sphereDiameter/Types.Default... | Diameter of cylinder on the connecting line from frame_a to frame_b [m] |
| Color | axisColor | Modelica.Mechanics.MultiBody... | Color of cylinder on the connecting line from frame_a to frame_b |
| SpecularCoefficient | specularCoefficient | world.defaultSpecularCoeffic... | Reflection of ambient light (= 0: light is completely absorbed) |
| if animation = true and showUniversalAxes | |||
| Distance | cylinderLength | world.defaultJointLength | Length of cylinders representing the two universal joint axes [m] |
| Distance | cylinderDiameter | world.defaultJointWidth | Diameter of cylinders representing the two universal joint axes [m] |
| Color | cylinderColor | Modelica.Mechanics.MultiBody... | Color of cylinders representing the two universal joint axes |
| Advanced | |||
| Boolean | checkTotalPower | false | = true, if total power flowing into this component shall be determined (must be zero) |
| Type | Name | Description |
|---|---|---|
| Frame_a | frame_a | Coordinate system fixed to the component with one cut-force and cut-torque |
| Frame_b | frame_b | Coordinate system fixed to the component with one cut-force and cut-torque |
| Frame_a | frame_ia | Coordinate system at origin of frame_a fixed at prismatic joint |
| Frame_b | frame_ib | Coordinate system at origin of frame_b fixed at prismatic joint |
| Flange_a | axis | 1-dim. translational flange that drives the prismatic joint |
| Flange_b | bearing | 1-dim. translational flange of the drive bearing of the prismatic joint |
model JointUPS "Universal - prismatic - spherical joint aggregation (no constraints, no potential states)" import SI = Modelica.SIunits; import Modelica.Mechanics.MultiBody.Types; extends Interfaces.PartialTwoFramesDoubleSize;Modelica.Mechanics.MultiBody.Interfaces.Frame_a frame_ia "Coordinate system at origin of frame_a fixed at prismatic joint"; Modelica.Mechanics.MultiBody.Interfaces.Frame_b frame_ib "Coordinate system at origin of frame_b fixed at prismatic joint"; Modelica.Mechanics.Translational.Interfaces.Flange_a axis "1-dim. translational flange that drives the prismatic joint"; Modelica.Mechanics.Translational.Interfaces.Flange_b bearing "1-dim. translational flange of the drive bearing of the prismatic joint"; parameter Boolean animation=true "= true, if animation shall be enabled"; parameter Boolean showUniversalAxes=true " = true, if universal joint shall be visualized with two cylinders, otherwise with a sphere (provided animation=true)"; parameter Modelica.Mechanics.MultiBody.Types.Axis n1_a={0,0,1} "Axis 1 of universal joint resolved in frame_a (axis 2 is orthogonal to axis 1 and to line from universal to spherical joint)"; parameter SI.Position nAxis_ia[3]={1,0,0} "Axis vector along line from origin of frame_a to origin of frame_b, resolved in frame_ia"; parameter SI.Position s_offset=0 "Relative distance offset (distance between frame_a and frame_b = s(t) + s_offset)"; parameter SI.Diameter sphereDiameter=world.defaultJointLength "Diameter of spheres representing the spherical joints"; input Types.Color sphereColor=Modelica.Mechanics.MultiBody.Types.Defaults.JointColor "Color of spheres representing the spherical joints"; parameter SI.Diameter axisDiameter=sphereDiameter/Types.Defaults. JointRodDiameterFraction "Diameter of cylinder on the connecting line from frame_a to frame_b"; input Types.Color axisColor=Modelica.Mechanics.MultiBody.Types.Defaults.SensorColor "Color of cylinder on the connecting line from frame_a to frame_b"; input Types.SpecularCoefficient specularCoefficient = world.defaultSpecularCoefficient "Reflection of ambient light (= 0: light is completely absorbed)"; parameter SI.Distance cylinderLength=world.defaultJointLength "Length of cylinders representing the two universal joint axes"; parameter SI.Distance cylinderDiameter=world.defaultJointWidth "Diameter of cylinders representing the two universal joint axes"; input Types.Color cylinderColor=Modelica.Mechanics.MultiBody.Types.Defaults.JointColor "Color of cylinders representing the two universal joint axes"; parameter Boolean checkTotalPower=false "= true, if total power flowing into this component shall be determined (must be zero)"; final parameter Real eAxis_ia[3](each final unit="1")=Modelica.Math.Vectors.normalize( nAxis_ia,0.0) "Unit vector from origin of frame_a to origin of frame_b, resolved in frame_ia"; final parameter Real e2_ia[3](each final unit="1")=Modelica.Math.Vectors.normalize( cross(n1_a, eAxis_ia),0.0) "Unit vector in direction of second rotation axis of universal joint, resolved in frame_ia"; final parameter Real e3_ia[3](each final unit="1")=cross(eAxis_ia, e2_ia) "Unit vector perpendicular to eAxis_ia and e2_ia, resolved in frame_ia"; SI.Position s "Relative distance between frame_a and frame_b along axis nAxis = s + s_offset"; SI.Force f "= axis.f (driving force in the axis; = -bearing.f)"; SI.Length axisLength "Distance between frame_a and frame_b"; SI.Power totalPower "Total power flowing into this element, if checkTotalPower=true (otherwise dummy)"; protected SI.Force f_c_a[3] "frame_ia.f resolved in frame_a"; SI.Torque t_cd_a[3] "frame_ia.t + frame_ib.t resolved in frame_a"; SI.Force f_bd_a[3] "frame_b.f + frame_ib.f resolved in frame_a"; SI.Position rAxis_0[3] "Position vector from origin of frame_a to origin of frame_b resolved in world frame"; SI.Position rAxis_a[3] "Position vector from origin of frame_a to origin of frame_b resolved in frame_a"; Real eAxis_a[3](each final unit="1") "Unit vector in direction of rAxis_a, resolved in frame_a"; Real e2_a[3](each final unit="1") "Unit vector in direction of second rotation axis of universal joint, resolved in frame_a"; Real e3_a[3](each final unit="1") "Unit vector perpendicular to eAxis_a and e2_a, resolved in frame_a"; Real n2_a[3](each final unit="1") "Vector in direction of second rotation axis of universal joint, resolved in frame_a"; Real length2_n2_a(unit="m2") "Square of length of vector n2_a"; SI.Length length_n2_a "Length of vector n2_a"; Real der_rAxis_a_L[3](each unit="1/s") "= der(rAxis_a)/axisLength"; SI.AngularVelocity w_rel_ia1[3]; Frames.Orientation R_ia1_a; Frames.Orientation R_ia2_a; Frames.Orientation R_ia_a "Rotation from frame_a to frame_ia"; // Real T_ia_a[3, 3] "Transformation matrix from frame_a to frame_ia"; Visualizers.Advanced.Shape axisCylinder( shapeType="cylinder", color=axisColor, specularCoefficient=specularCoefficient, length=axisLength, width=axisDiameter, height=axisDiameter, lengthDirection=eAxis_ia, widthDirection=e2_ia, r=frame_ia.r_0, R=frame_ia.R) if world.enableAnimation and animation; Visualizers.Advanced.Shape sphericalShape_b( shapeType="sphere", color=sphereColor, specularCoefficient=specularCoefficient, length=sphereDiameter, width=sphereDiameter, height=sphereDiameter, lengthDirection={1,0,0}, widthDirection={0,1,0}, r_shape={-0.5,0,0}*sphereDiameter, r=frame_b.r_0, R=frame_b.R) if world.enableAnimation and animation; Visualizers.Advanced.Shape sphericalShape_a( shapeType="sphere", color=sphereColor, specularCoefficient=specularCoefficient, length=sphereDiameter, width=sphereDiameter, height=sphereDiameter, lengthDirection={1,0,0}, widthDirection={0,1,0}, r_shape={-0.5,0,0}*sphereDiameter, r=frame_a.r_0, R=frame_a.R) if world.enableAnimation and animation; Visualizers.Advanced.Shape universalShape1( shapeType="cylinder", color=cylinderColor, specularCoefficient=specularCoefficient, length=cylinderLength, width=cylinderDiameter, height=cylinderDiameter, lengthDirection=n1_a, widthDirection={0,1,0}, r_shape=-n1_a*(cylinderLength/2), r=frame_a.r_0, R=frame_a.R) if world.enableAnimation and animation and showUniversalAxes; Visualizers.Advanced.Shape universalShape2( shapeType="cylinder", color=cylinderColor, specularCoefficient=specularCoefficient, length=cylinderLength, width=cylinderDiameter, height=cylinderDiameter, lengthDirection=e2_ia, widthDirection={0,1,0}, r_shape=-e2_ia*(cylinderLength/2), r=frame_ia.r_0, R=frame_ia.R) if world.enableAnimation and animation and showUniversalAxes; equation Connections.branch(frame_a.R, frame_ia.R); Connections.branch(frame_ia.R, frame_ib.R); // Translational flanges axisLength = s + s_offset; bearing.s = 0; axis.s = s; axis.f = f; // Position vector rAxis from frame_a to frame_b rAxis_0 = frame_b.r_0 - frame_a.r_0; rAxis_a = Frames.resolve2(frame_a.R, rAxis_0); /* Determine relative Rotation R_rel_c from frame_a to frame_ia and absolute rotation of frame_a.R. */ axisLength = sqrt(rAxis_0*rAxis_0); assert(axisLength > 1.0e-15, " Distance between frame_a and frame_b of a JointUPS joint became zero. This is not allowed. If this occurs during initialization, the initial conditions are probably wrong."); eAxis_a = rAxis_a/axisLength; n2_a = cross(n1_a, eAxis_a); length2_n2_a = n2_a*n2_a; assert(noEvent(length2_n2_a > 1.e-10), " A Modelica.Mechanics.MultiBody.Joints.Assemblies.JointUPS joint (consisting of a universal, prismatic and spherical joint) is in the singular configuration of the universal joint. This means that axis 1 of the universal joint defined via parameter \"n1_a\" is parallel to vector \"eAxis_ia\" that is directed from the origin of frame_a to the origin of frame_b. You may try to use another \"n1_a\" vector. "); length_n2_a = sqrt(length2_n2_a); e2_a = n2_a/length_n2_a; e3_a = cross(eAxis_a, e2_a); /* The statements below are an efficient implementation of the original equations: T_ia_a = [eAxis_ia, e2_ia, e3_ia]*transpose([eAxis_a, e2_a, e3_a]); R_ia_a = Frames.from_T(T_ia_a, Frames.TransformationMatrices.angularVelocity2(T_ia_a, der(T_ia_a))); To perform this, the rotation is split into two parts: R_ia_a : Rotation object from frame_a to frame_ia R_ia1_a: Rotation object from frame_a to frame_ia1 (frame that is fixed in frame_ia such that x-axis is along the rod axis) T = transpose([eAxis_a, e2_a, e3_a]; w = w_rel_ia1 R_ia2_a: Fixed rotation object from frame_ia1 to frame_ia T = [eAxis_a, e2_ia, e3_ia]; w = zeros(3) The difficult part is to compute w_rel_ia1: w_rel_ia1 = [ e3_a*der(e2_a); -e3_a*der(eAxis_a); e2_a*der(eAxis_a)] der(eAxis_a) is directly given, since eAxis_a is a function of translational quantities only. der(eAxis_a) = (der(rAxis_a) - eAxis_a*(eAxis_a*der(rAxis_a)))/axisLength der(n2_a) = cross(n1_a, der(eAxis_a)) der(e2_a) = (der(n2_a) - e2_a*(e2_a*der(n2_a)))/length_n2_a Inserting these equations in w_rel_ia1 results in: e3_a*der(eAxis_a) = e3_a*der(rAxis_a)/axisLength // e3_a*eAxis_a = 0 e2_a*der(eAxis_a) = e2_a*der(rAxis_a)/axisLength // e2_a*eAxis_a = 0 e3_a*der(e2_a) = e3_a*der(n2_a)/lenght_n2_a // e3_a*e2_a = 0 = e3_a*cross(n1_a, der(eAxis_a))/length_n2_a = e3_a*cross(n1_a, der(rAxis_a) - eAxis_a*(eAxis_a*der(rAxis_a)))/(length_n2_a*axisLength) = e3_a*cross(n1_a, der(rAxis_a))/(length_n2_a*axisLength) Furthermore, we have: rAxis_a = resolve2(frame_a.R, rAxis_0); der(rAxis_a) = resolve2(frame_a.R, der(rAxis_0)) - cross(frame_a.R.w, rAxis_a)); */ der_rAxis_a_L = (Frames.resolve2(frame_a.R, der(rAxis_0)) - cross(frame_a. R.w, rAxis_a))/axisLength; w_rel_ia1 = {e3_a*cross(n1_a, der_rAxis_a_L)/length_n2_a,-e3_a* der_rAxis_a_L,e2_a*der_rAxis_a_L}; R_ia1_a = Frames.from_T(transpose([eAxis_a, e2_a, e3_a]), w_rel_ia1); R_ia2_a = Frames.from_T([eAxis_ia, e2_ia, e3_ia], zeros(3)); R_ia_a = Frames.absoluteRotation(R_ia1_a, R_ia2_a); /* T_ia_a = [eAxis_ia, e2_ia, e3_ia]*transpose([eAxis_a, e2_a, e3_a]); R_ia_a = Frames.from_T(T_ia_a, Frames.TransformationMatrices.angularVelocity2 (T_ia_a, der(T_ia_a))); */ // Compute kinematic quantities of frame_ia and frame_ib frame_ia.r_0 = frame_a.r_0; frame_ib.r_0 = frame_b.r_0; frame_ia.R = Frames.absoluteRotation(frame_a.R, R_ia_a); frame_ib.R = frame_ia.R; /* In the following formulas f_a, f_b, f_ia, f_ib, t_a, t_b, t_ia, t_ib are the forces and torques at frame_a, frame_b, frame_ia, frame_ib respectively, resolved in frame_a. eAxis, e2, e3 are the unit vectors resolved in frame_a. Torque balance at the rod around the origin of frame_a: 0 = t_a + t_ia + t_ib + cross(rAxis, (f_b+f_ib)) with rAxis = axisLength*eAxis f_bd = f_b + f_ib f_bd = f*eAxis + f_bd[2]*e2 + f_bd[3]*e3 follows: 0 = t_a + t_ia + axisLength*(f_bd[2]*e_z - f_bd[3]*e_y) The projection of t_a with respect to universal joint axes vanishes: e1*t_a = 0 e2*t_a = 0 Therefore: 0 = e1*(t_ia + t_ib) + axisLength*f_bd[2]*(e1*e3) 0 = e2*(t_ia + t_ib) - axisLength*f_bd[3] or f_bd = f*eAxis - e2*(e1*(t_ia+t_ib))/(axisLength*(e1*e3)) + e3*(e2*(t_ia+t_ib))/axisLength Force balance: 0 = f_a + f_bd + f_ia */ f_c_a = Frames.resolve1(R_ia_a, frame_ia.f); t_cd_a = Frames.resolve1(R_ia_a, frame_ia.t + frame_ib.t); f_bd_a = -eAxis_a*f - e2_a*((n1_a*t_cd_a)/(axisLength*(n1_a*e3_a))) + e3_a*((e2_a*t_cd_a)/axisLength); zeros(3) = frame_b.f + Frames.resolveRelative(frame_ib.f, frame_ib.R, frame_b.R) - Frames.resolveRelative(f_bd_a, frame_a.R, frame_b.R); zeros(3) = frame_b.t; zeros(3) = frame_a.f + f_c_a + f_bd_a; zeros(3) = frame_a.t + t_cd_a + cross(rAxis_a, f_bd_a); // Measure power for test purposes if checkTotalPower then totalPower = frame_a.f*Frames.resolve2(frame_a.R, der(frame_a.r_0)) + frame_b.f*Frames.resolve2(frame_b.R, der(frame_b.r_0)) + frame_ia.f* Frames.resolve2(frame_ia.R, der(frame_ia.r_0)) + frame_ib.f* Frames.resolve2(frame_ib.R, der(frame_ib.r_0)) + frame_a.t* Frames.angularVelocity2(frame_a.R) + frame_b.t* Frames.angularVelocity2(frame_b.R) + frame_ia.t* Frames.angularVelocity2(frame_ia.R) + frame_ib.t* Frames.angularVelocity2(frame_ib.R) + axis.f*der(axis.s) + bearing.f* der(bearing.s); else totalPower = 0; end if;end JointUPS;
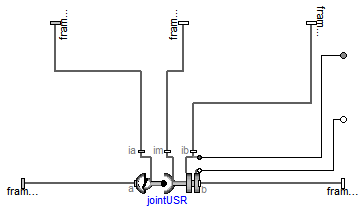
 Modelica.Mechanics.MultiBody.Joints.Assemblies.JointUSR
Modelica.Mechanics.MultiBody.Joints.Assemblies.JointUSR
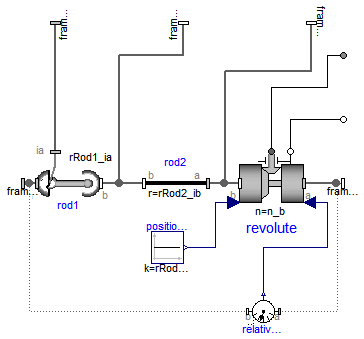
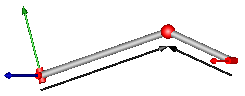
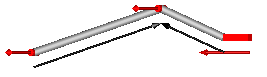
This component consists of a universal joint at frame_a, a revolute joint at frame_b and a spherical joint which is connected via rod1 to the universal and via rod2 to the revolute joint, see the default animation in the following figure (the axes vectors are not part of the default animation):

This joint aggregation has no mass and no inertia and introduces neither constraints nor potential state variables. It should be used in kinematic loops whenever possible since the non-linear system of equations introduced by this joint aggregation is solved analytically (i.e., a solution is always computed, if a unique solution exists).
The universal joint is defined in the following way:
The definition of axis 2 of the universal joint is performed according to the most often occuring case. In a future release, axis 2 might be explicitly definable via a parameter. However, the treatment is much more complicated and the number of operations is considerably higher, if axis 2 is not orthogonal to axis 1 and to the connecting rod.
Note, there is a singularity when axis 1 and the connecting rod are parallel to each other. Therefore, if possible n1_a should be selected in such a way that it is perpendicular to rRod1_ia in the initial configuration (i.e., the distance to the singularity is as large as possible).
The rest of this joint aggregation is defined by the following parameters:
An additional frame_ia is present. It is fixed in the rod connecting the universal and the spherical joint at the origin of frame_a. The placement of frame_ia on the rod is implicitly defined by the universal joint (frame_a and frame_ia coincide when the angles of the two revolute joints of the universal joint are zero) and by parameter vector rRod1_ia, the position vector from the origin of frame_a to the spherical joint, resolved in frame_ia.
An additional frame_ib is present. It is fixed in the rod connecting the revolute and the spherical joint at the side of the revolute joint that is connected to this rod (= rod2.frame_a = revolute.frame_a).
An additional frame_im is present. It is fixed in the rod connecting the revolute and the spherical joint at the side of the spherical joint that is connected to this rod (= rod2.frame_b). It is always parallel to frame_ib.
The easiest way to define the parameters of this joint is by moving the MultiBody system in a reference configuration where all frames of all components are parallel to each other (alternatively, at least frame_a and frame_ia of the JointUSR joint should be parallel to each other when defining an instance of this component).
In the public interface of the JointUSR joint, the following (final) parameters are provided:
parameter Real rod1Length(unit="m") "Length of rod 1"; parameter Real eRod1_ia[3] "Unit vector along rod 1, resolved in frame_ia"; parameter Real e2_ia [3] "Unit vector along axis 2, resolved in frame_ia";
This allows a more convenient definition of data which is related to rod 1. For example, if a box shall be connected at frame_ia directing from the origin of frame_a to the middle of rod 1, this might be defined as:
Modelica.Mechanics.MultiBody.Joints.Assemblies.JointUSP jointUSR(rRod1_ia={1.2, 1, 0.2});
Modelica.Mechanics.MultiBody.Visualizers.FixedShape shape(shapeType = "box",
lengthDirection = jointUSR.eRod1_ia,
widthDirection = jointUSR.e2_ia,
length = jointUSR.rod1Length/2,
width = jointUSR.rod1Length/10);
equation
connect(jointUSP.frame_ia, shape.frame_a);
Extends from Interfaces.PartialTwoFramesDoubleSize (Base model for components providing two frame connectors + outer world + assert to guarantee that the component is connected (default icon size is factor 2 larger as usual)).
| Type | Name | Default | Description |
|---|---|---|---|
| Boolean | animation | true | = true, if animation shall be enabled |
| Boolean | showUniversalAxes | true | = true, if universal joint shall be visualized with two cylinders, otherwise with a sphere (provided animation=true) |
| Axis | n1_a | {0,0,1} | Axis 1 of universal joint fixed and resolved in frame_a (axis 2 is orthogonal to axis 1 and to rod 1) [1] |
| Axis | n_b | {0,0,1} | Axis of revolute joint fixed and resolved in frame_b [1] |
| Position | rRod1_ia[3] | {1,0,0} | Vector from origin of frame_a to spherical joint, resolved in frame_ia [m] |
| Position | rRod2_ib[3] | {-1,0,0} | Vector from origin of frame_ib to spherical joint, resolved in frame_ib [m] |
| Angle_deg | phi_offset | 0 | Relative angle offset of revolute joint (angle = phi(t) + from_deg(phi_offset)) [deg] |
| Angle_deg | phi_guess | 0 | Select the configuration such that at initial time |phi(t0) - from_deg(phi_guess)|is minimal [deg] |
| Animation | |||
| if animation = true | |||
| Diameter | sphereDiameter | world.defaultJointLength | Diameter of the spheres representing the universal and the spherical joint [m] |
| Color | sphereColor | Modelica.Mechanics.MultiBody... | Color of the spheres representing the universal and the spherical joint |
| Diameter | rod1Diameter | sphereDiameter/Types.Default... | Diameter of rod 1 connecting the universal and the spherical joint [m] |
| Color | rod1Color | Modelica.Mechanics.MultiBody... | Color of rod 1 connecting the universal and the spherical joint |
| Diameter | rod2Diameter | rod1Diameter | Diameter of rod 2 connecting the revolute and the spherical joint [m] |
| Color | rod2Color | rod1Color | Color of rod 2 connecting the revolute and the spherical joint |
| Diameter | revoluteDiameter | world.defaultJointWidth | Diameter of cylinder representing the revolute joint [m] |
| Distance | revoluteLength | world.defaultJointLength | Length of cylinder representing the revolute joint [m] |
| Color | revoluteColor | Modelica.Mechanics.MultiBody... | Color of cylinder representing the revolute joint |
| SpecularCoefficient | specularCoefficient | world.defaultSpecularCoeffic... | Reflection of ambient light (= 0: light is completely absorbed) |
| if animation = true and showUniversalAxes | |||
| Distance | cylinderLength | world.defaultJointLength | Length of cylinders representing the two universal joint axes [m] |
| Distance | cylinderDiameter | world.defaultJointWidth | Diameter of cylinders representing the two universal joint axes [m] |
| Color | cylinderColor | Modelica.Mechanics.MultiBody... | Color of cylinders representing the two universal joint axes |
| Advanced | |||
| Boolean | checkTotalPower | false | = true, if total power flowing into this component shall be determined (must be zero) |
| Type | Name | Description |
|---|---|---|
| Frame_a | frame_a | Coordinate system fixed to the component with one cut-force and cut-torque |
| Frame_b | frame_b | Coordinate system fixed to the component with one cut-force and cut-torque |
| Frame_a | frame_ia | Coordinate system at origin of frame_a fixed at connecting rod of universal and spherical joint |
| Frame_b | frame_ib | Coordinate system at origin of frame_b fixed at connecting rod of spherical and revolute joint |
| Frame_b | frame_im | Coordinate system at origin of spherical joint fixed at connecting rod of spherical and revolute joint |
| Flange_a | axis | 1-dim. rotational flange that drives the revolute joint |
| Flange_b | bearing | 1-dim. rotational flange of the drive bearing of the revolute joint |
model JointUSR "Universal - spherical - revolute joint aggregation (no constraints, no potential states)" import SI = Modelica.SIunits; import Cv = Modelica.SIunits.Conversions; import Modelica.Mechanics.MultiBody.Types; extends Interfaces.PartialTwoFramesDoubleSize;Modelica.Mechanics.MultiBody.Interfaces.Frame_a frame_ia "Coordinate system at origin of frame_a fixed at connecting rod of universal and spherical joint"; Modelica.Mechanics.MultiBody.Interfaces.Frame_b frame_ib "Coordinate system at origin of frame_b fixed at connecting rod of spherical and revolute joint"; Modelica.Mechanics.MultiBody.Interfaces.Frame_b frame_im "Coordinate system at origin of spherical joint fixed at connecting rod of spherical and revolute joint"; Modelica.Mechanics.Rotational.Interfaces.Flange_a axis "1-dim. rotational flange that drives the revolute joint"; Modelica.Mechanics.Rotational.Interfaces.Flange_b bearing "1-dim. rotational flange of the drive bearing of the revolute joint"; parameter Boolean animation=true "= true, if animation shall be enabled"; parameter Boolean showUniversalAxes=true " = true, if universal joint shall be visualized with two cylinders, otherwise with a sphere (provided animation=true)"; parameter Modelica.Mechanics.MultiBody.Types.Axis n1_a={0,0,1} "Axis 1 of universal joint fixed and resolved in frame_a (axis 2 is orthogonal to axis 1 and to rod 1)"; parameter Modelica.Mechanics.MultiBody.Types.Axis n_b={0,0,1} "Axis of revolute joint fixed and resolved in frame_b"; parameter SI.Position rRod1_ia[3]={1,0,0} "Vector from origin of frame_a to spherical joint, resolved in frame_ia"; parameter SI.Position rRod2_ib[3]={-1,0,0} "Vector from origin of frame_ib to spherical joint, resolved in frame_ib"; parameter Cv.NonSIunits.Angle_deg phi_offset=0 "Relative angle offset of revolute joint (angle = phi(t) + from_deg(phi_offset))"; parameter Cv.NonSIunits.Angle_deg phi_guess=0 "Select the configuration such that at initial time |phi(t0) - from_deg(phi_guess)|is minimal"; parameter SI.Diameter sphereDiameter=world.defaultJointLength "Diameter of the spheres representing the universal and the spherical joint"; input Types.Color sphereColor=Modelica.Mechanics.MultiBody.Types.Defaults. JointColor "Color of the spheres representing the universal and the spherical joint"; parameter SI.Diameter rod1Diameter=sphereDiameter/Types.Defaults. JointRodDiameterFraction "Diameter of rod 1 connecting the universal and the spherical joint"; input Types.Color rod1Color=Modelica.Mechanics.MultiBody.Types.Defaults. RodColor "Color of rod 1 connecting the universal and the spherical joint"; parameter SI.Diameter rod2Diameter=rod1Diameter "Diameter of rod 2 connecting the revolute and the spherical joint"; input Types.Color rod2Color=rod1Color "Color of rod 2 connecting the revolute and the spherical joint"; parameter SI.Diameter revoluteDiameter=world.defaultJointWidth "Diameter of cylinder representing the revolute joint"; parameter SI.Distance revoluteLength=world.defaultJointLength "Length of cylinder representing the revolute joint"; input Types.Color revoluteColor=Modelica.Mechanics.MultiBody.Types. Defaults.JointColor "Color of cylinder representing the revolute joint"; input Types.SpecularCoefficient specularCoefficient = world.defaultSpecularCoefficient "Reflection of ambient light (= 0: light is completely absorbed)"; parameter SI.Distance cylinderLength=world.defaultJointLength "Length of cylinders representing the two universal joint axes"; parameter SI.Distance cylinderDiameter=world.defaultJointWidth "Diameter of cylinders representing the two universal joint axes"; input Types.Color cylinderColor=Modelica.Mechanics.MultiBody.Types.Defaults.JointColor "Color of cylinders representing the two universal joint axes"; parameter Boolean checkTotalPower=false "= true, if total power flowing into this component shall be determined (must be zero)"; final parameter Real eRod1_ia[3](each final unit="1")=rod1.eRod_ia "Unit vector from origin of frame_a to origin of spherical joint, resolved in frame_ia"; final parameter Real e2_ia[3](each final unit="1")=rod1.e2_ia "Unit vector in direction of axis 2 of universal joint, resolved in frame_ia"; final parameter SI.Distance rod1Length=rod1.rodLength "Length of rod 1 (= distance between universal and spherical joint"; SI.Power totalPower "Total power flowing into this element, if checkTotalPower=true (otherwise dummy)"; SI.Position aux "Denominator used to compute force in rod connecting universal and spherical joint"; SI.Force f_rod "Constraint force in direction of the rod (positive, if rod is pressed)";Modelica.Mechanics.MultiBody.Joints.Internal.RevoluteWithLengthConstraint revolute( animation=animation, lengthConstraint=rod1Length, n=n_b, phi_offset=phi_offset, phi_guess=phi_guess, cylinderDiameter=revoluteDiameter, cylinderLength=revoluteLength, cylinderColor=revoluteColor, specularCoefficient=specularCoefficient); Modelica.Mechanics.MultiBody.Joints.UniversalSpherical rod1( animation=animation, showUniversalAxes=showUniversalAxes, rRod_ia=rRod1_ia, n1_a=n1_a, sphereDiameter=sphereDiameter, sphereColor=sphereColor, rodWidth=rod1Diameter, rodHeight=rod1Diameter, rodColor=rod1Color, cylinderLength=cylinderLength, cylinderDiameter=cylinderDiameter, cylinderColor=cylinderColor, specularCoefficient=specularCoefficient, kinematicConstraint=false, constraintResidue=rod1.f_rod - f_rod); Modelica.Mechanics.MultiBody.Parts.FixedTranslation rod2( animation=animation, width=rod2Diameter, height=rod2Diameter, color=rod2Color, specularCoefficient=specularCoefficient, r=rRod2_ib); Sensors.RelativePosition relativePosition(resolveInFrame=Modelica.Mechanics.MultiBody.Types.ResolveInFrameAB.frame_a); Modelica.Blocks.Sources.Constant position_b[3](k=rRod2_ib); equation // Connections.root(frame_ib.R); /* Compute the unknown force in the rod of the rod1 joint by a torque balance at the revolute joint: 0 = revolute.frame_b.t + frame_ib.t + frame_im.t + cross(rRod2_ib, frame_im.f) + cross(r_ib, -rod1.f_b_a1) + cross(r_ib, Frames.resolve2(rod1.R_rel, rod1.f_rod*rod1.eRod1_ia)) The condition is that the projection of the torque in the revolute joint along the axis of the revolute joint is equal to the driving axis torque in the flange: -revolute.tau = revolute.e*frame_b.t Therefore, we have tau = e*(frame_ib.t + frame_im.t + cross(rRod2_ib, frame_im.f) + cross(rRod2_ib, -rod1.f_b_a1)) + e*cross(rRod2_ib, Frames.resolve2(rod1.R_rel, rod1.f_rod*rod1.eRod_a)) = e*(frame_ib.t + frame_im.t + cross(rRod2_ib, frame_im.f) + cross(rRod2_ib, -rod.f_b_a1)) + rod1.f_rod*e*cross(rRod2_ib, Frames.resolve2(rod1.R_rel, rod1.eRod_a)) Solving this equation for f_rod results in f_rod = (-tau - e*(frame_ib.t + frame_im.t + cross(rRod2_ib, frame_im.f) + cross(rRod2_ib, -rod1.f_b_a1))) / (cross(e,rRod2_ib)*Frames.resolve2(rod1.R_rel, rod1.eRod_a))) Additionally, a guard against division by zero is introduced f_rod is passed to component JointsUSR.rod1 via variable "constraintResidue" in the Advanced menu */ aux = cross(revolute.e, rRod2_ib)*Frames.resolveRelative(rod1.eRod_a, rod1.frame_a.R, rod1.frame_b.R); f_rod = (-revolute.tau - revolute.e*(frame_ib.t + frame_im.t + cross( rRod2_ib, frame_im.f) - cross(rRod2_ib, Frames.resolveRelative(rod1. f_b_a1, rod1.frame_a.R, rod1.frame_b.R))))/noEvent(if abs(aux) < 1.e-10 then 1.e-10 else aux); // Measure power for test purposes if checkTotalPower then totalPower = frame_a.f*Frames.resolve2(frame_a.R, der(frame_a.r_0)) + frame_b.f*Frames.resolve2(frame_b.R, der(frame_b.r_0)) + frame_ia.f* Frames.resolve2(frame_ia.R, der(frame_ia.r_0)) + frame_ib.f* Frames.resolve2(frame_ib.R, der(frame_ib.r_0)) + frame_im.f* Frames.resolve2(frame_im.R, der(frame_im.r_0)) + frame_a.t* Frames.angularVelocity2(frame_a.R) + frame_b.t* Frames.angularVelocity2(frame_b.R) + frame_ia.t* Frames.angularVelocity2(frame_ia.R) + frame_ib.t* Frames.angularVelocity2(frame_ib.R) + frame_im.t* Frames.angularVelocity2(frame_im.R) + axis.tau*der(axis.phi) + bearing.tau*der(bearing.phi); else totalPower = 0; end if;connect(revolute.frame_b, rod2.frame_a); connect(rod2.frame_b, rod1.frame_b); connect(revolute.frame_a, frame_b); connect(rod2.frame_a, frame_ib); connect(rod1.frame_a, frame_a); connect(relativePosition.frame_b, frame_a); connect(relativePosition.frame_a, frame_b); connect(position_b.y, revolute.position_b); connect(rod2.frame_b, frame_im); connect(rod1.frame_ia, frame_ia); connect(revolute.axis, axis); connect(relativePosition.r_rel, revolute.position_a); connect(revolute.bearing, bearing); end JointUSR;
 Modelica.Mechanics.MultiBody.Joints.Assemblies.JointUSP
Modelica.Mechanics.MultiBody.Joints.Assemblies.JointUSP
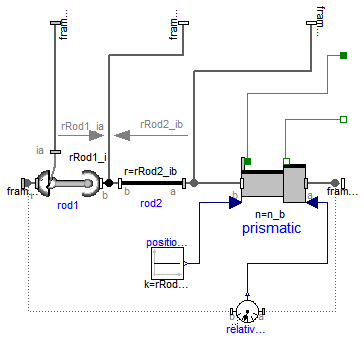
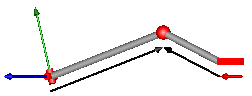
This component consists of a universal joint at frame_a, a prismatic joint at frame_b and a spherical joint which is connected via rod1 to the universal and via rod2 to the prismatic joint, see the default animation in the following figure (the axes vectors are not part of the default animation):

This joint aggregation has no mass and no inertia and introduces neither constraints nor potential state variables. It should be used in kinematic loops whenever possible since the non-linear system of equations introduced by this joint aggregation is solved analytically (i.e., a solution is always computed, if a unique solution exists).
The universal joint is defined in the following way:
The definition of axis 2 of the universal joint is performed according to the most often occuring case. In a future release, axis 2 might be explicitly definable via a parameter. However, the treatment is much more complicated and the number of operations is considerably higher, if axis 2 is not orthogonal to axis 1 and to the connecting rod.
Note, there is a singularity when axis 1 and the connecting rod are parallel to each other. Therefore, if possible n1_a should be selected in such a way that it is perpendicular to rRod1_ia in the initial configuration (i.e., the distance to the singularity is as large as possible).
The rest of this joint aggregation is defined by the following parameters:
An additional frame_ia is present. It is fixed in the rod connecting the universal and the spherical joint at the origin of frame_a. The placement of frame_ia on the rod is implicitly defined by the universal joint (frame_a and frame_ia coincide when the angles of the two revolute joints of the universal joint are zero) and by parameter vector rRod1_ia, the position vector from the origin of frame_a to the spherical joint, resolved in frame_ia.
An additional frame_ib is present. It is fixed in the rod connecting the prismatic and the spherical joint at the side of the prismatic joint that is connected to this rod (= rod2.frame_a = prismatic.frame_a). It is always parallel to frame_b.
An additional frame_im is present. It is fixed in the rod connecting the prismatic and the spherical joint at the side of the spherical joint that is connected to this rod (= rod2.frame_b). It is always parallel to frame_b.
The easiest way to define the parameters of this joint is by moving the MultiBody system in a reference configuration where all frames of all components are parallel to each other (alternatively, at least frame_a and frame_ia of the JointUSP joint should be parallel to each other when defining an instance of this component).
In the public interface of the JointUSP joint, the following (final) parameters are provided:
parameter Real rod1Length(unit="m") "Length of rod 1"; parameter Real eRod1_ia[3] "Unit vector along rod 1, resolved in frame_ia"; parameter Real e2_ia [3] "Unit vector along axis 2, resolved in frame_ia";
This allows a more convenient definition of data which is related to rod 1. For example, if a box shall be connected at frame_ia directing from the origin of frame_a to the middle of rod 1, this might be defined as:
Modelica.Mechanics.MultiBody.Joints.Assemblies.JointUSP jointUSP(rRod1_ia={1.2, 1, 0.2});
Modelica.Mechanics.MultiBody.Visualizers.FixedShape shape(shapeType = "box",
lengthDirection = jointUSP.eRod1_ia,
widthDirection = jointUSP.e2_ia,
length = jointUSP.rod1Length/2,
width = jointUSP.rod1Length/10);
equation
connect(jointUSP.frame_ia, shape.frame_a);
Extends from Interfaces.PartialTwoFramesDoubleSize (Base model for components providing two frame connectors + outer world + assert to guarantee that the component is connected (default icon size is factor 2 larger as usual)).
| Type | Name | Default | Description |
|---|---|---|---|
| Boolean | animation | true | = true, if animation shall be enabled |
| Boolean | showUniversalAxes | true | = true, if universal joint shall be visualized with two cylinders, otherwise with a sphere (provided animation=true) |
| Axis | n1_a | {0,0,1} | Axis 1 of universal joint fixed and resolved in frame_a (axis 2 is orthogonal to axis 1 and to rod 1) [1] |
| Axis | n_b | {-1,0,0} | Axis of prismatic joint fixed and resolved in frame_b [1] |
| Position | rRod1_ia[3] | {1,0,0} | Vector from origin of frame_a to spherical joint, resolved in frame_ia [m] |
| Position | rRod2_ib[3] | {-1,0,0} | Vector from origin of frame_ib to spherical joint, resolved in frame_ib (frame_ib is parallel to frame_b) [m] |
| Position | s_offset | 0 | Relative distance offset of prismatic joint (distance between the prismatic joint frames = s(t) + s_offset) [m] |
| Position | s_guess | 0 | Select the configuration such that at initial time |s(t0)-s_guess|is minimal [m] |
| Animation | |||
| if animation = true | |||
| Diameter | sphereDiameter | world.defaultJointLength | Diameter of the spheres representing the universal and the spherical joint [m] |
| Color | sphereColor | Modelica.Mechanics.MultiBody... | Color of the spheres representing the universal and the spherical joint |
| Diameter | rod1Diameter | sphereDiameter/Types.Default... | Diameter of rod 1 connecting the universal and the spherical joint [m] |
| Color | rod1Color | Modelica.Mechanics.MultiBody... | Color of rod 1 connecting the universal and the spherical joint |
| Diameter | rod2Diameter | rod1Diameter | Diameter of rod 2 connecting the prismatic and the spherical joint [m] |
| Color | rod2Color | rod1Color | Color of rod 2 connecting the prismatic and the spherical joint |
| Axis | boxWidthDirection | {0,1,0} | Vector in width direction of prismatic joint, resolved in frame_b [1] |
| Distance | boxWidth | world.defaultJointWidth | Width of prismatic joint box [m] |
| Distance | boxHeight | boxWidth | Height of prismatic joint box [m] |
| Color | boxColor | sphereColor | Color of prismatic joint box |
| SpecularCoefficient | specularCoefficient | world.defaultSpecularCoeffic... | Reflection of ambient light (= 0: light is completely absorbed) |
| if animation = true and showUniversalAxes | |||
| Distance | cylinderLength | world.defaultJointLength | Length of cylinders representing the two universal joint axes [m] |
| Distance | cylinderDiameter | world.defaultJointWidth | Diameter of cylinders representing the two universal joint axes [m] |
| Color | cylinderColor | Modelica.Mechanics.MultiBody... | Color of cylinders representing the two universal joint axes |
| Advanced | |||
| Boolean | checkTotalPower | false | = true, if total power flowing into this component shall be determined (must be zero) |
| Type | Name | Description |
|---|---|---|
| Frame_a | frame_a | Coordinate system fixed to the component with one cut-force and cut-torque |
| Frame_b | frame_b | Coordinate system fixed to the component with one cut-force and cut-torque |
| Frame_a | frame_ia | Coordinate system at origin of frame_a fixed at connecting rod of universal and spherical joint |
| Frame_b | frame_ib | Coordinate system at origin of frame_b fixed at connecting rod of spherical and prismatic joint |
| Frame_b | frame_im | Coordinate system at origin of spherical joint fixed at connecting rod of spherical and prismatic joint |
| Flange_a | axis | 1-dim. translational flange that drives the prismatic joint |
| Flange_b | bearing | 1-dim. translational flange of the drive bearing of the prismatic joint |
model JointUSP "Universal - spherical - prismatic joint aggregation (no constraints, no potential states)" import SI = Modelica.SIunits; import Modelica.Mechanics.MultiBody.Types; extends Interfaces.PartialTwoFramesDoubleSize;Modelica.Mechanics.MultiBody.Interfaces.Frame_a frame_ia "Coordinate system at origin of frame_a fixed at connecting rod of universal and spherical joint"; Modelica.Mechanics.MultiBody.Interfaces.Frame_b frame_ib "Coordinate system at origin of frame_b fixed at connecting rod of spherical and prismatic joint"; Modelica.Mechanics.MultiBody.Interfaces.Frame_b frame_im "Coordinate system at origin of spherical joint fixed at connecting rod of spherical and prismatic joint"; Modelica.Mechanics.Translational.Interfaces.Flange_a axis "1-dim. translational flange that drives the prismatic joint"; Modelica.Mechanics.Translational.Interfaces.Flange_b bearing "1-dim. translational flange of the drive bearing of the prismatic joint"; parameter Boolean animation=true "= true, if animation shall be enabled"; parameter Boolean showUniversalAxes=true " = true, if universal joint shall be visualized with two cylinders, otherwise with a sphere (provided animation=true)"; parameter Modelica.Mechanics.MultiBody.Types.Axis n1_a={0,0,1} "Axis 1 of universal joint fixed and resolved in frame_a (axis 2 is orthogonal to axis 1 and to rod 1)"; parameter Modelica.Mechanics.MultiBody.Types.Axis n_b={-1,0,0} "Axis of prismatic joint fixed and resolved in frame_b"; parameter SI.Position rRod1_ia[3]={1,0,0} "Vector from origin of frame_a to spherical joint, resolved in frame_ia"; parameter SI.Position rRod2_ib[3]={-1,0,0} "Vector from origin of frame_ib to spherical joint, resolved in frame_ib (frame_ib is parallel to frame_b)"; parameter SI.Position s_offset=0 "Relative distance offset of prismatic joint (distance between the prismatic joint frames = s(t) + s_offset)"; parameter SI.Position s_guess=0 "Select the configuration such that at initial time |s(t0)-s_guess|is minimal"; parameter SI.Diameter sphereDiameter=world.defaultJointLength "Diameter of the spheres representing the universal and the spherical joint"; input Types.Color sphereColor=Modelica.Mechanics.MultiBody.Types.Defaults.JointColor "Color of the spheres representing the universal and the spherical joint"; parameter SI.Diameter rod1Diameter=sphereDiameter/Types.Defaults. JointRodDiameterFraction "Diameter of rod 1 connecting the universal and the spherical joint"; input Types.Color rod1Color=Modelica.Mechanics.MultiBody.Types.Defaults.RodColor "Color of rod 1 connecting the universal and the spherical joint"; parameter SI.Diameter rod2Diameter=rod1Diameter "Diameter of rod 2 connecting the prismatic and the spherical joint"; input Types.Color rod2Color=rod1Color "Color of rod 2 connecting the prismatic and the spherical joint"; parameter Types.Axis boxWidthDirection={0,1,0} "Vector in width direction of prismatic joint, resolved in frame_b"; parameter SI.Distance boxWidth=world.defaultJointWidth "Width of prismatic joint box"; parameter SI.Distance boxHeight=boxWidth "Height of prismatic joint box"; input Types.Color boxColor=sphereColor "Color of prismatic joint box"; input Types.SpecularCoefficient specularCoefficient = world.defaultSpecularCoefficient "Reflection of ambient light (= 0: light is completely absorbed)"; parameter SI.Distance cylinderLength=world.defaultJointLength "Length of cylinders representing the two universal joint axes"; parameter SI.Distance cylinderDiameter=world.defaultJointWidth "Diameter of cylinders representing the two universal joint axes"; input Types.Color cylinderColor=Modelica.Mechanics.MultiBody.Types.Defaults.JointColor "Color of cylinders representing the two universal joint axes"; parameter Boolean checkTotalPower=false "= true, if total power flowing into this component shall be determined (must be zero)"; final parameter Real eRod1_ia[3](each final unit="1")=rod1.eRod_ia "Unit vector from origin of frame_a to origin of spherical joint, resolved in frame_ia"; final parameter Real e2_ia[3](each final unit="1")=rod1.e2_ia "Unit vector in direction of axis 2 of universal joint, resolved in frame_ia"; final parameter SI.Distance rod1Length=rod1.rodLength "Length of rod 1 (= distance between universal and spherical joint"; SI.Force f_rod "Constraint force in direction of the rod (positive, if rod is pressed)"; SI.Power totalPower "Total power flowing into this element, if checkTotalPower=true (otherwise dummy)";Modelica.Mechanics.MultiBody.Joints.Internal.PrismaticWithLengthConstraint prismatic( animation=animation, length=rod1.rodLength, n=n_b, s_offset=s_offset, s_guess=s_guess, boxWidthDirection=boxWidthDirection, boxWidth=boxWidth, boxHeight=boxHeight, boxColor=boxColor, specularCoefficient=specularCoefficient); Modelica.Mechanics.MultiBody.Joints.UniversalSpherical rod1( animation=animation, showUniversalAxes=showUniversalAxes, rRod_ia=rRod1_ia, n1_a=n1_a, sphereDiameter=sphereDiameter, sphereColor=sphereColor, rodWidth=rod1Diameter, rodHeight=rod1Diameter, rodColor=rod1Color, specularCoefficient=specularCoefficient, cylinderLength=cylinderLength, cylinderDiameter=cylinderDiameter, cylinderColor=cylinderColor, kinematicConstraint=false, constraintResidue=rod1.f_rod - f_rod); Modelica.Mechanics.MultiBody.Parts.FixedTranslation rod2( animation=animation, r=rRod2_ib, width=rod2Diameter, height=rod2Diameter, specularCoefficient=specularCoefficient, color=rod2Color); Sensors.RelativePosition relativePosition(resolveInFrame=Modelica.Mechanics.MultiBody.Types.ResolveInFrameAB.frame_a); Modelica.Blocks.Sources.Constant position_b[3](k=rRod2_ib); protected Real aux "Denominator used to compute force in rod connecting universal and spherical joint"; equation /* Compute the unknown force in rod1 connecting the universal and the spherical joint by a force balance at the prismatic joint 0 = -prismatic.frame_b.f + frame_ib.f + frame_im.f - rod1.frame_b.f The force at rod1.frame_b is split into two parts: rod1.frame_b.f = Frames.resolve2(rod1.R_rel, rod1.f_b_a1 - rod1.f_rod*rod1.eRod_a) where rod1.f_rod is the unknown force in rod1. The condition is that the projection of the force in the prismatic joint along the axis of its translation axis is equal to the driving axis force in the flange: -prismatic.f = prismatic.e*prismatic.frame_b.f Therefore, we have with e=prismatic.e and f=prismatic.f -f = e*(frame_ib.f + frame_im.f - Frames.resolve2(rod1.R_rel, rod1.f_b_a1 - rod1.f_rod*rod1.eRod_a)) = e*(frame_ib.f + frame_im.f - Frames.resolve2(rod1.R_rel, rod1.f_b_a1) + rod1.f_rod*Frames.resolve2(rod1.R_rel, rod1.eRod_a)) Solving this equation for f_rod results in rod1.f_rod = -(f+e*(frame_ib.f + frame_im.f - Frames.resolve2(rod1.R_rel, rod1.f_b_a1)) /(e*Frames.resolve2(rod1.R_rel, rod1.eRod_a)) Additionally, a guard against division by zero is introduced */ aux = prismatic.e*Frames.resolveRelative(rod1.eRod_a, rod1.frame_a.R, rod1.frame_b.R); f_rod = (-prismatic.f - prismatic.e*(frame_ib.f + frame_im.f - Frames.resolveRelative(rod1.f_b_a1, rod1.frame_a.R, rod1.frame_b.R)))/ noEvent(if abs(aux) < 1.e-10 then 1.e-10 else aux); // Measure power for test purposes if checkTotalPower then totalPower = frame_a.f*Frames.resolve2(frame_a.R, der(frame_a.r_0)) + frame_b.f*Frames.resolve2(frame_b.R, der(frame_b.r_0)) + frame_ia.f* Frames.resolve2(frame_ia.R, der(frame_ia.r_0)) + frame_ib.f* Frames.resolve2(frame_ib.R, der(frame_ib.r_0)) + frame_im.f* Frames.resolve2(frame_im.R, der(frame_im.r_0)) + frame_a.t* Frames.angularVelocity2(frame_a.R) + frame_b.t* Frames.angularVelocity2(frame_b.R) + frame_ia.t* Frames.angularVelocity2(frame_ia.R) + frame_ib.t* Frames.angularVelocity2(frame_ib.R) + frame_im.t* Frames.angularVelocity2(frame_im.R) + axis.f*der(axis.s) + bearing.f* der(bearing.s); else totalPower = 0; end if;connect(prismatic.frame_b, rod2.frame_a); connect(rod2.frame_b, rod1.frame_b); connect(prismatic.frame_a, frame_b); connect(rod2.frame_a, frame_ib); connect(rod1.frame_a, frame_a); connect(relativePosition.frame_b, frame_a); connect(relativePosition.frame_a, frame_b); connect(rod2.frame_b, frame_im); connect(rod1.frame_ia, frame_ia); connect(position_b.y, prismatic.position_b); connect(prismatic.axis, axis); connect(prismatic.bearing, bearing); connect(relativePosition.r_rel, prismatic.position_a); end JointUSP;
 Modelica.Mechanics.MultiBody.Joints.Assemblies.JointSSR
Modelica.Mechanics.MultiBody.Joints.Assemblies.JointSSR
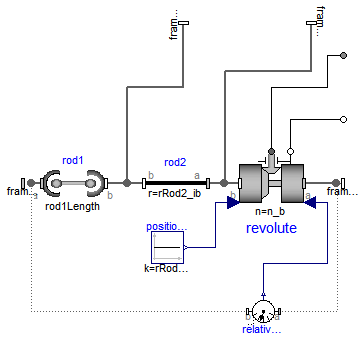
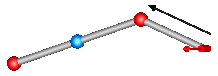
This component consists of a spherical joint 1 at frame_a, a revolute joint at frame_b and a spherical joint 2 which is connected via rod 1 to the spherical joint 1 and via rod 2 to the revolute joint, see the default animation in the following figure (the axes vectors are not part of the default animation):

Besides an optional point mass in the middle of rod 1, this joint aggregation has no mass and no inertia, and introduces neither constraints nor potential state variables. It should be used in kinematic loops whenever possible since the non-linear system of equations introduced by this joint aggregation is solved analytically (i.e., a solution is always computed, if a unique solution exists).
An additional frame_ib is present. It is fixed in rod 2 connecting the revolute and the spherical joint at the side of the revolute joint that is connected to this rod (= rod2.frame_a = revolute.frame_a).
An additional frame_im is present. It is fixed in rod 2 connecting the revolute and the spherical joint at the side of spherical joint 2 that is connected to this rod (= rod2.frame_b). It is always parallel to frame_ib.
The easiest way to define the parameters of this joint is by moving the MultiBody system in a reference configuration where all frames of all components are parallel to each other (alternatively, at least frame_b and frame_ib of the JointSSR joint should be parallel to each other when defining an instance of this component).
Extends from Interfaces.PartialTwoFramesDoubleSize (Base model for components providing two frame connectors + outer world + assert to guarantee that the component is connected (default icon size is factor 2 larger as usual)).
| Type | Name | Default | Description |
|---|---|---|---|
| Boolean | animation | true | = true, if animation shall be enabled |
| Boolean | showMass | true | = true, if point mass on rod 1 shall be shown (provided animation = true and rod1Mass > 0) |
| Length | rod1Length | Distance between the origins of the two spherical joints [m] | |
| Mass | rod1Mass | 0 | Mass of rod 1 (= point mass located in middle of rod connecting the two spherical joints) [kg] |
| Axis | n_b | {0,0,1} | Axis of revolute joint fixed and resolved in frame_b [1] |
| Position | rRod2_ib[3] | {1,0,0} | Vector from origin of frame_ib to spherical joint in the middle, resolved in frame_ib [m] |
| Angle_deg | phi_offset | 0 | Relative angle offset of revolute joint (angle = phi(t) + from_deg(phi_offset)) [deg] |
| Angle_deg | phi_guess | 0 | Select the configuration such that at initial time |phi(t0) - from_deg(phi_guess)|is minimal [deg] |
| Animation | |||
| if animation = true | |||
| Diameter | sphereDiameter | world.defaultJointLength | Diameter of the spheres representing the two spherical joints [m] |
| Color | sphereColor | Modelica.Mechanics.MultiBody... | Color of the spheres representing the two spherical joints |
| Diameter | rod1Diameter | sphereDiameter/Types.Default... | Diameter of rod 1 connecting the two spherical joints [m] |
| Color | rod1Color | Modelica.Mechanics.MultiBody... | Color of rod 1 connecting the two spherical joint |
| Diameter | rod2Diameter | rod1Diameter | Diameter of rod 2 connecting the revolute joint and spherical joint 2 [m] |
| Color | rod2Color | rod1Color | Color of rod 2 connecting the revolute joint and spherical joint 2 |
| Diameter | revoluteDiameter | world.defaultJointWidth | Diameter of cylinder representing the revolute joint [m] |
| Distance | revoluteLength | world.defaultJointLength | Length of cylinder representing the revolute joint [m] |
| Color | revoluteColor | Modelica.Mechanics.MultiBody... | Color of cylinder representing the revolute joint |
| SpecularCoefficient | specularCoefficient | world.defaultSpecularCoeffic... | Reflection of ambient light (= 0: light is completely absorbed) |
| Advanced | |||
| Boolean | checkTotalPower | false | = true, if total power flowing into this component shall be determined (must be zero) |
| Type | Name | Description |
|---|---|---|
| Frame_a | frame_a | Coordinate system fixed to the component with one cut-force and cut-torque |
| Frame_b | frame_b | Coordinate system fixed to the component with one cut-force and cut-torque |
| Frame_b | frame_ib | Coordinate system at origin of frame_b fixed at connecting rod of spherical and revolute joint |
| Frame_b | frame_im | Coordinate system at origin of spherical joint in the middle fixed at connecting rod of spherical and revolute joint |
| Flange_a | axis | 1-dim. rotational flange that drives the revolute joint |
| Flange_b | bearing | 1-dim. rotational flange of the drive bearing of the revolute joint |
model JointSSR "Spherical - spherical - revolute joint aggregation with mass (no constraints, no potential states)" import SI = Modelica.SIunits; import Cv = Modelica.SIunits.Conversions; import Modelica.Mechanics.MultiBody.Types; extends Interfaces.PartialTwoFramesDoubleSize;Modelica.Mechanics.MultiBody.Interfaces.Frame_b frame_ib "Coordinate system at origin of frame_b fixed at connecting rod of spherical and revolute joint"; Modelica.Mechanics.MultiBody.Interfaces.Frame_b frame_im "Coordinate system at origin of spherical joint in the middle fixed at connecting rod of spherical and revolute joint"; Modelica.Mechanics.Rotational.Interfaces.Flange_a axis "1-dim. rotational flange that drives the revolute joint"; Modelica.Mechanics.Rotational.Interfaces.Flange_b bearing "1-dim. rotational flange of the drive bearing of the revolute joint"; parameter Boolean animation=true "= true, if animation shall be enabled"; parameter Boolean showMass=true "= true, if point mass on rod 1 shall be shown (provided animation = true and rod1Mass > 0)"; parameter SI.Length rod1Length(min=Modelica.Constants.eps, start = 1) "Distance between the origins of the two spherical joints "; parameter SI.Mass rod1Mass(min=0)=0 "Mass of rod 1 (= point mass located in middle of rod connecting the two spherical joints)"; parameter Modelica.Mechanics.MultiBody.Types.Axis n_b={0,0,1} "Axis of revolute joint fixed and resolved in frame_b"; parameter SI.Position rRod2_ib[3]={1,0,0} "Vector from origin of frame_ib to spherical joint in the middle, resolved in frame_ib"; parameter Cv.NonSIunits.Angle_deg phi_offset=0 "Relative angle offset of revolute joint (angle = phi(t) + from_deg(phi_offset))"; parameter Cv.NonSIunits.Angle_deg phi_guess=0 "Select the configuration such that at initial time |phi(t0) - from_deg(phi_guess)|is minimal"; parameter SI.Diameter sphereDiameter=world.defaultJointLength "Diameter of the spheres representing the two spherical joints"; input Types.Color sphereColor=Modelica.Mechanics.MultiBody.Types.Defaults. JointColor "Color of the spheres representing the two spherical joints"; parameter SI.Diameter rod1Diameter=sphereDiameter/Types.Defaults. JointRodDiameterFraction "Diameter of rod 1 connecting the two spherical joints"; input Types.Color rod1Color=Modelica.Mechanics.MultiBody.Types.Defaults. RodColor "Color of rod 1 connecting the two spherical joint"; parameter SI.Diameter rod2Diameter=rod1Diameter "Diameter of rod 2 connecting the revolute joint and spherical joint 2"; input Types.Color rod2Color=rod1Color "Color of rod 2 connecting the revolute joint and spherical joint 2"; parameter SI.Diameter revoluteDiameter=world.defaultJointWidth "Diameter of cylinder representing the revolute joint"; parameter SI.Distance revoluteLength=world.defaultJointLength "Length of cylinder representing the revolute joint"; input Types.Color revoluteColor=Modelica.Mechanics.MultiBody.Types. Defaults.JointColor "Color of cylinder representing the revolute joint"; input Types.SpecularCoefficient specularCoefficient = world.defaultSpecularCoefficient "Reflection of ambient light (= 0: light is completely absorbed)"; parameter Boolean checkTotalPower=false "= true, if total power flowing into this component shall be determined (must be zero)"; SI.Position aux "Denominator used to compute force in rod connecting universal and spherical joint"; SI.Force f_rod "Constraint force in direction of the rod (positive, if rod is pressed)"; SI.Power totalPower "Total power flowing into this element, if checkTotalPower=true (otherwise dummy)";Modelica.Mechanics.MultiBody.Joints.Internal.RevoluteWithLengthConstraint revolute( animation=animation, lengthConstraint=rod1Length, n=n_b, phi_offset=phi_offset, phi_guess=phi_guess, cylinderDiameter=revoluteDiameter, cylinderLength=revoluteLength, cylinderColor=revoluteColor, specularCoefficient=specularCoefficient); Modelica.Mechanics.MultiBody.Joints.SphericalSpherical rod1( animation=animation, showMass=showMass, m=rod1Mass, rodLength=rod1Length, rodDiameter=rod1Diameter, sphereDiameter=sphereDiameter, rodColor=rod1Color, specularCoefficient=specularCoefficient, kinematicConstraint=false, sphereColor=sphereColor, constraintResidue=rod1.f_rod - f_rod); Modelica.Mechanics.MultiBody.Parts.FixedTranslation rod2( animation=animation, width=rod2Diameter, height=rod2Diameter, color=rod2Color, specularCoefficient=specularCoefficient, r=rRod2_ib); Sensors.RelativePosition relativePosition(resolveInFrame=Modelica.Mechanics.MultiBody.Types.ResolveInFrameAB.frame_a); Modelica.Blocks.Sources.Constant position_b[3](k=rRod2_ib); equation /* Compute the unknown force in the rod of the rod1 joint by a torque balance at the revolute joint: 0 = frame_b.t + frame_ib.t + frame_im.t + cross(rRod2_ib, frame_im.f) + cross(rRod2_ib, -rod1.f_b_a1) + cross(rRod2_ib, Frames.resolve2(rod1.R_rel, rod1.f_rod*rod1.eRod_a)) The condition is that the projection of the torque in the revolute joint along the axis of the revolute joint is equal to the driving axis torque in the flange: -revolute.tau = revolute.e*frame_b.t Therefore, we have with e=revolute.e and tau=revolute.tau tau = e*(frame_ib.t + frame_im.t + cross(rRod2_ib, frame_im.f) + cross(rRod2_ib, -rod1.f_b_a1)) + e*cross(rRod2_ib, Frames.resolve2(rod1.R_rel, rod1.f_rod*rod1.eRod_a)) = e*(frame_ib.t + frame_im.t + cross(rRod2_ib, frame_im.f) + cross(rRod2_ib, -rod.f_b_a1)) + rod1.f_rod*e*cross(rRod2_ib, Frames.resolve2(rod1.R_rel, rod1.eRod_a)) Solving this equation for f_rod results in rod1.f_rod = (tau - e*(frame_ib.t + frame_im.t + cross(rRod2_ib, frame_im.f) + cross(rRod2_ib, -rod1.f_b_a1))) / (cross(e,rRod2_ib)*Frames.resolve2(rod1.R_rel, rod1.eRod_a))) Additionally, a guard against division by zero is introduced */ aux = cross(revolute.e, rRod2_ib)*Frames.resolveRelative(rod1.eRod_a, rod1.frame_a.R, rod1.frame_b.R); f_rod = (-revolute.tau - revolute.e*(frame_ib.t + frame_im.t + cross( rRod2_ib, frame_im.f) - cross(rRod2_ib, Frames.resolveRelative(rod1. f_b_a1, rod1.frame_a.R, rod1.frame_b.R))))/noEvent(if abs(aux) < 1.e-10 then 1.e-10 else aux); // Measure power for test purposes if checkTotalPower then totalPower = frame_a.f*Frames.resolve2(frame_a.R, der(frame_a.r_0)) + frame_b.f*Frames.resolve2(frame_b.R, der(frame_b.r_0)) + frame_ib.f* Frames.resolve2(frame_ib.R, der(frame_ib.r_0)) + frame_im.f* Frames.resolve2(frame_im.R, der(frame_im.r_0)) + frame_a.t* Frames.angularVelocity2(frame_a.R) + frame_b.t* Frames.angularVelocity2(frame_b.R) + frame_ib.t* Frames.angularVelocity2(frame_ib.R) + frame_im.t* Frames.angularVelocity2(frame_im.R) + axis.tau*der(axis.phi) + bearing.tau*der(bearing.phi) + (-rod1Mass)*(der(rod1.v_CM_0) - world.gravityAcceleration(rod1.r_CM_0))*rod1.v_CM_0; else totalPower = 0; end if;connect(revolute.frame_b, rod2.frame_a); connect(rod2.frame_b, rod1.frame_b); connect(revolute.frame_a, frame_b); connect(rod2.frame_a, frame_ib); connect(rod1.frame_a, frame_a); connect(relativePosition.frame_b, frame_a); connect(relativePosition.frame_a, frame_b); connect(position_b.y, revolute.position_b); connect(revolute.axis, axis); connect(rod2.frame_b, frame_im); connect(relativePosition.r_rel, revolute.position_a); connect(revolute.bearing, bearing); end JointSSR;
 Modelica.Mechanics.MultiBody.Joints.Assemblies.JointSSP
Modelica.Mechanics.MultiBody.Joints.Assemblies.JointSSP
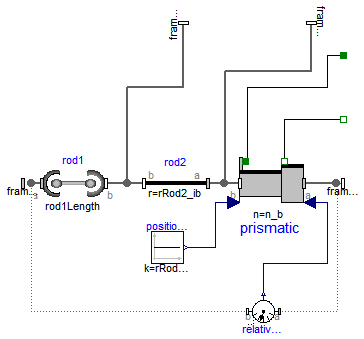
This component consists of a spherical joint 1 at frame_a, a prismatic joint at frame_b and a spherical joint 2 which is connected via rod 1 to the spherical joint 1 and via rod 2 to the prismatic joint, see the default animation in the following figure (the axes vectors are not part of the default animation):

Besides an optional point mass in the middle of rod 1, this joint aggregation has no mass and no inertia, and introduces neither constraints nor potential state variables. It should be used in kinematic loops whenever possible since the non-linear system of equations introduced by this joint aggregation is solved analytically (i.e., a solution is always computed, if a unique solution exists).
An additional frame_ib is present. It is fixed in rod 2 connecting the prismatic and the spherical joint at the side of the prismatic joint that is connected to this rod (= rod2.frame_a = prismatic.frame_a).
An additional frame_im is present. It is fixed in rod 2 connecting the prismatic and the spherical joint at the side of spherical joint 2 that is connected to this rod (= rod2.frame_b). It is always parallel to frame_ib.
The easiest way to define the parameters of this joint is by moving the MultiBody system in a reference configuration where all frames of all components are parallel to each other (alternatively, at least frame_b and frame_ib of the JointSSP joint should be parallel to each other when defining an instance of this component).
Extends from Interfaces.PartialTwoFramesDoubleSize (Base model for components providing two frame connectors + outer world + assert to guarantee that the component is connected (default icon size is factor 2 larger as usual)).
| Type | Name | Default | Description |
|---|---|---|---|
| Boolean | animation | true | = true, if animation shall be enabled |
| Boolean | showMass | true | = true, if point mass on rod 1 shall be shown (provided animation = true and rod1Mass > 0) |
| Length | rod1Length | Distance between the origins of the two spherical joints [m] | |
| Mass | rod1Mass | 0 | Mass of rod 1 (= point mass located in middle of rod connecting the two spherical joints) [kg] |
| Axis | n_b | {0,0,1} | Axis of prismatic joint fixed and resolved in frame_b [1] |
| Position | rRod2_ib[3] | {1,0,0} | Vector from origin of frame_ib to spherical joint in the middle, resolved in frame_ib [m] |
| Position | s_offset | 0 | Relative distance offset of prismatic joint (distance between frame_b and frame_ib = s(t) + s_offset) [m] |
| Position | s_guess | 0 | Select the configuration such that at initial time |s(t0)-s_guess|is minimal [m] |
| Animation | |||
| if animation = true | |||
| Diameter | sphereDiameter | world.defaultJointLength | Diameter of the spheres representing the two spherical joints [m] |
| Color | sphereColor | Modelica.Mechanics.MultiBody... | Color of the spheres representing the two spherical joints |
| Diameter | rod1Diameter | sphereDiameter/Types.Default... | Diameter of rod 1 connecting the two spherical joints [m] |
| Color | rod1Color | Modelica.Mechanics.MultiBody... | Color of rod 1 connecting the two spherical joint |
| Diameter | rod2Diameter | rod1Diameter | Diameter of rod 2 connecting the revolute joint and spherical joint 2 [m] |
| Color | rod2Color | rod1Color | Color of rod 2 connecting the revolute joint and spherical joint 2 |
| Axis | boxWidthDirection | {0,1,0} | Vector in width direction of prismatic joint box, resolved in frame_b [1] |
| Distance | boxWidth | world.defaultJointWidth | Width of prismatic joint box [m] |
| Distance | boxHeight | boxWidth | Height of prismatic joint box [m] |
| Color | boxColor | Modelica.Mechanics.MultiBody... | Color of prismatic joint box |
| SpecularCoefficient | specularCoefficient | world.defaultSpecularCoeffic... | Reflection of ambient light (= 0: light is completely absorbed) |
| Advanced | |||
| Boolean | checkTotalPower | false | = true, if total power flowing into this component shall be determined (must be zero) |
| Type | Name | Description |
|---|---|---|
| Frame_a | frame_a | Coordinate system fixed to the component with one cut-force and cut-torque |
| Frame_b | frame_b | Coordinate system fixed to the component with one cut-force and cut-torque |
| Frame_b | frame_ib | Coordinate system at origin of frame_b fixed at connecting rod of spherical and prismatic joint |
| Frame_b | frame_im | Coordinate system at origin of spherical joint in the middle fixed at connecting rod of spherical and prismatic joint |
| Flange_a | axis | 1-dim. translational flange that drives the prismatic joint |
| Flange_b | bearing | 1-dim. translational flange of the drive bearing of the prismatic joint |
model JointSSP "Spherical - spherical - prismatic joint aggregation with mass (no constraints, no potential states)" import SI = Modelica.SIunits; import Cv = Modelica.SIunits.Conversions; import Modelica.Mechanics.MultiBody.Types; extends Interfaces.PartialTwoFramesDoubleSize;Modelica.Mechanics.MultiBody.Interfaces.Frame_b frame_ib "Coordinate system at origin of frame_b fixed at connecting rod of spherical and prismatic joint"; Modelica.Mechanics.MultiBody.Interfaces.Frame_b frame_im "Coordinate system at origin of spherical joint in the middle fixed at connecting rod of spherical and prismatic joint"; Modelica.Mechanics.Translational.Interfaces.Flange_a axis "1-dim. translational flange that drives the prismatic joint"; Modelica.Mechanics.Translational.Interfaces.Flange_b bearing "1-dim. translational flange of the drive bearing of the prismatic joint"; parameter Boolean animation=true "= true, if animation shall be enabled"; parameter Boolean showMass=true "= true, if point mass on rod 1 shall be shown (provided animation = true and rod1Mass > 0)"; parameter SI.Length rod1Length(min=Modelica.Constants.eps, start = 1) "Distance between the origins of the two spherical joints "; parameter SI.Mass rod1Mass(min=0)=0 "Mass of rod 1 (= point mass located in middle of rod connecting the two spherical joints)"; parameter Modelica.Mechanics.MultiBody.Types.Axis n_b={0,0,1} "Axis of prismatic joint fixed and resolved in frame_b"; parameter SI.Position rRod2_ib[3]={1,0,0} "Vector from origin of frame_ib to spherical joint in the middle, resolved in frame_ib"; parameter SI.Position s_offset=0 "Relative distance offset of prismatic joint (distance between frame_b and frame_ib = s(t) + s_offset)"; parameter SI.Position s_guess=0 "Select the configuration such that at initial time |s(t0)-s_guess|is minimal"; parameter SI.Diameter sphereDiameter=world.defaultJointLength "Diameter of the spheres representing the two spherical joints"; input Types.Color sphereColor=Modelica.Mechanics.MultiBody.Types.Defaults. JointColor "Color of the spheres representing the two spherical joints"; parameter SI.Diameter rod1Diameter=sphereDiameter/Types.Defaults. JointRodDiameterFraction "Diameter of rod 1 connecting the two spherical joints"; input Types.Color rod1Color=Modelica.Mechanics.MultiBody.Types.Defaults. RodColor "Color of rod 1 connecting the two spherical joint"; parameter SI.Diameter rod2Diameter=rod1Diameter "Diameter of rod 2 connecting the revolute joint and spherical joint 2"; input Types.Color rod2Color=rod1Color "Color of rod 2 connecting the revolute joint and spherical joint 2"; parameter Types.Axis boxWidthDirection={0,1,0} "Vector in width direction of prismatic joint box, resolved in frame_b"; parameter SI.Distance boxWidth=world.defaultJointWidth "Width of prismatic joint box"; parameter SI.Distance boxHeight=boxWidth "Height of prismatic joint box"; input Types.Color boxColor=Modelica.Mechanics.MultiBody.Types.Defaults.JointColor "Color of prismatic joint box"; input Types.SpecularCoefficient specularCoefficient = world.defaultSpecularCoefficient "Reflection of ambient light (= 0: light is completely absorbed)"; parameter Boolean checkTotalPower=false "= true, if total power flowing into this component shall be determined (must be zero)"; Real aux "Denominator used to compute force in rod connecting universal and spherical joint"; SI.Force f_rod "Constraint force in direction of the rod (positive, if rod is pressed)"; SI.Power totalPower "Total power flowing into this element, if checkTotalPower=true (otherwise dummy)";Modelica.Mechanics.MultiBody.Joints.Internal.PrismaticWithLengthConstraint prismatic( animation=animation, length=rod1Length, n=n_b, s_offset=s_offset, s_guess=s_guess, boxWidthDirection=boxWidthDirection, boxWidth=boxWidth, boxHeight=boxHeight, specularCoefficient=specularCoefficient, boxColor=boxColor); Modelica.Mechanics.MultiBody.Joints.SphericalSpherical rod1( animation=animation, showMass=showMass, m=rod1Mass, rodLength=rod1Length, rodDiameter=rod1Diameter, sphereDiameter=sphereDiameter, rodColor=rod1Color, kinematicConstraint=false, specularCoefficient=specularCoefficient, sphereColor=sphereColor, constraintResidue=rod1.f_rod - f_rod); Modelica.Mechanics.MultiBody.Parts.FixedTranslation rod2( animation=animation, width=rod2Diameter, height=rod2Diameter, specularCoefficient=specularCoefficient, color=rod2Color, r=rRod2_ib); Sensors.RelativePosition relativePosition(resolveInFrame=Modelica.Mechanics.MultiBody.Types.ResolveInFrameAB.frame_a); Modelica.Blocks.Sources.Constant position_b[3](k=rRod2_ib); equation /* Compute the unknown force in the rod of the rod1 joint by a force balance: 0 = frame_b.f + frame_ib.f + frame_im.f + Frames.resolve2(rod1.R_rel, rod1.f_rod*rod1.eRod_a) The condition is that the projection of the force in the prismatic joint along the axis of the prismatic joint is equal to the driving axis force in the flange: -prismatic.f = prismatic.e*frame_b.f Therefore, we have with e=prismatic.e and f=prismatic.f f = e*(frame_ib.f + frame_im.f + Frames.resolve2(rod1.R_rel, rod1.f_rod*rod1.eRod_a)) = e*(frame_ib.f + frame_im.f + rod1.f_rod*Frames.resolve2(rod1.R_rel, rod1.eRod_a)) Solving this equation for f_rod results in rod1.f_rod = (f - e*(frame_ib.f + frame_im.f)) / (e*Frames.resolve2(rod1.R_rel, rod1.eRod_a)) Additionally, a guard against division by zero is introduced */ aux = prismatic.e*Frames.resolveRelative(rod1.eRod_a, rod1.frame_a.R, rod1.frame_b.R); f_rod = (-prismatic.f - prismatic.e*(frame_ib.f + frame_im.f))/ noEvent(if abs(aux) < 1.e-10 then 1.e-10 else aux); // Measure power for test purposes if checkTotalPower then totalPower = frame_a.f*Frames.resolve2(frame_a.R, der(frame_a.r_0)) + frame_b.f*Frames.resolve2(frame_b.R, der(frame_b.r_0)) + frame_ib.f* Frames.resolve2(frame_ib.R, der(frame_ib.r_0)) + frame_im.f* Frames.resolve2(frame_im.R, der(frame_im.r_0)) + frame_a.t* Frames.angularVelocity2(frame_a.R) + frame_b.t* Frames.angularVelocity2(frame_b.R) + frame_ib.t* Frames.angularVelocity2(frame_ib.R) + frame_im.t* Frames.angularVelocity2(frame_im.R) + axis.f*der(axis.s) + bearing.f* der(bearing.s) + (-rod1Mass)*(der(rod1.v_CM_0) - world.gravityAcceleration(rod1.r_CM_0))*rod1.v_CM_0; else totalPower = 0; end if;connect(prismatic.frame_b, rod2.frame_a); connect(rod2.frame_b, rod1.frame_b); connect(prismatic.frame_a, frame_b); connect(rod2.frame_a, frame_ib); connect(rod1.frame_a, frame_a); connect(relativePosition.frame_b, frame_a); connect(relativePosition.frame_a, frame_b); connect(position_b.y, prismatic.position_b); connect(prismatic.axis, axis); connect(prismatic.bearing, bearing); connect(rod2.frame_b, frame_im); connect(relativePosition.r_rel, prismatic.position_a); end JointSSP;
 Modelica.Mechanics.MultiBody.Joints.Assemblies.JointRRR
Modelica.Mechanics.MultiBody.Joints.Assemblies.JointRRR
This component consists of 3 revolute joints with parallel axes of rotation that are connected together by two rods, see the default animation in the following figure (the axes vectors are not part of the default animation):

This joint aggregation introduces neither constraints nor state variables and should therefore be used in kinematic loops whenever possible to avoid non-linear systems of equations. It is only meaningful to use this component in planar loops. Basically, the position and orientation of the 3 revolute joints as well as of frame_ia, frame_ib, and frame_im are calculated by solving analytically a non-linear equation, given the position and orientation at frame_a and at frame_b.
Connector frame_a is the "left" side of the first revolute joint whereas frame_ia is the "right side of this revolute joint, fixed in rod 1. Connector frame_b is the "right" side of the third revolute joint whereas frame_ib is the "left" side of this revolute joint, fixed in rod 2. Finally, connector frame_im is the connector at the "right" side of the revolute joint in the middle, fixed in rod 2.
The easiest way to define the parameters of this joint is by moving the MultiBody system in a reference configuration where all frames of all components are parallel to each other (alternatively, at least frame_a, frame_ia, frame_im, frame_ib, frame_b of the JointRRR joint should be parallel to each other when defining an instance of this component).
Basically, the JointRRR model consists internally of a universal - spherical - revolute joint aggregation (= JointUSR). In a planar loop this will behave as if 3 revolute joints with parallel axes are connected by rigid rods.
Extends from Interfaces.PartialTwoFramesDoubleSize (Base model for components providing two frame connectors + outer world + assert to guarantee that the component is connected (default icon size is factor 2 larger as usual)).
| Type | Name | Default | Description |
|---|---|---|---|
| Boolean | animation | true | = true, if animation shall be enabled |
| Axis | n_a | {0,0,1} | Axes of revolute joints resolved in frame_a (all axes are parallel to each other) [1] |
| Position | rRod1_ia[3] | {1,0,0} | Vector from origin of frame_a to revolute joint in the middle, resolved in frame_ia [m] |
| Position | rRod2_ib[3] | {-1,0,0} | Vector from origin of frame_ib to revolute joint in the middle, resolved in frame_ib [m] |
| Angle_deg | phi_offset | 0 | Relative angle offset of revolute joint at frame_b (angle = phi(t) + from_deg(phi_offset)) [deg] |
| Angle_deg | phi_guess | 0 | Select the configuration such that at initial time |phi(t0) - from_deg(phi_guess)|is minimal [deg] |
| Animation | |||
| if animation = true | |||
| Distance | cylinderLength | world.defaultJointLength | Length of cylinders representing the revolute joints [m] |
| Distance | cylinderDiameter | world.defaultJointWidth | Diameter of cylinders representing the revolute joints [m] |
| Color | cylinderColor | Modelica.Mechanics.MultiBody... | Color of cylinders representing the revolute joints |
| Diameter | rodDiameter | 1.1*cylinderDiameter | Diameter of the two rods connecting the revolute joints [m] |
| Color | rodColor | Modelica.Mechanics.MultiBody... | Color of the two rods connecting the revolute joint |
| SpecularCoefficient | specularCoefficient | world.defaultSpecularCoeffic... | Reflection of ambient light (= 0: light is completely absorbed) |
| Advanced | |||
| Boolean | checkTotalPower | false | = true, if total power flowing into this component shall be determined (must be zero) |
| Type | Name | Description |
|---|---|---|
| Frame_a | frame_a | Coordinate system fixed to the component with one cut-force and cut-torque |
| Frame_b | frame_b | Coordinate system fixed to the component with one cut-force and cut-torque |
| Frame_a | frame_ia | Coordinate system at origin of frame_a fixed at connecting rod of left and middle revolute joint |
| Frame_b | frame_ib | Coordinate system at origin of frame_b fixed at connecting rod of middle and right revolute joint |
| Frame_b | frame_im | Coordinate system at origin of revolute joint in the middle fixed at connecting rod of middle and right revolute joint |
| Flange_a | axis | 1-dim. rotational flange that drives the right revolute joint at frame_b |
| Flange_b | bearing | 1-dim. rotational flange of the drive bearing of the right revolute joint at frame_b |
model JointRRR "Planar revolute - revolute - revolute joint aggregation (no constraints, no potential states)" import SI = Modelica.SIunits; import Cv = Modelica.SIunits.Conversions; import Modelica.Mechanics.MultiBody.Types; extends Interfaces.PartialTwoFramesDoubleSize;Modelica.Mechanics.MultiBody.Interfaces.Frame_a frame_ia "Coordinate system at origin of frame_a fixed at connecting rod of left and middle revolute joint"; Modelica.Mechanics.MultiBody.Interfaces.Frame_b frame_ib "Coordinate system at origin of frame_b fixed at connecting rod of middle and right revolute joint"; Modelica.Mechanics.MultiBody.Interfaces.Frame_b frame_im "Coordinate system at origin of revolute joint in the middle fixed at connecting rod of middle and right revolute joint"; Modelica.Mechanics.Rotational.Interfaces.Flange_a axis "1-dim. rotational flange that drives the right revolute joint at frame_b"; Modelica.Mechanics.Rotational.Interfaces.Flange_b bearing "1-dim. rotational flange of the drive bearing of the right revolute joint at frame_b"; parameter Boolean animation=true "= true, if animation shall be enabled"; parameter Modelica.Mechanics.MultiBody.Types.Axis n_a={0,0,1} "Axes of revolute joints resolved in frame_a (all axes are parallel to each other)"; final parameter Real n_b[3](each final unit="1",fixed=false) = {0,0,1} "Axis of revolute joint fixed and resolved in frame_b"; parameter SI.Position rRod1_ia[3]={1,0,0} "Vector from origin of frame_a to revolute joint in the middle, resolved in frame_ia"; parameter SI.Position rRod2_ib[3]={-1,0,0} "Vector from origin of frame_ib to revolute joint in the middle, resolved in frame_ib"; parameter Cv.NonSIunits.Angle_deg phi_offset=0 "Relative angle offset of revolute joint at frame_b (angle = phi(t) + from_deg(phi_offset))"; parameter Cv.NonSIunits.Angle_deg phi_guess=0 "Select the configuration such that at initial time |phi(t0) - from_deg(phi_guess)|is minimal"; parameter SI.Distance cylinderLength=world.defaultJointLength "Length of cylinders representing the revolute joints"; parameter SI.Distance cylinderDiameter=world.defaultJointWidth "Diameter of cylinders representing the revolute joints"; input Types.Color cylinderColor=Modelica.Mechanics.MultiBody.Types.Defaults.JointColor "Color of cylinders representing the revolute joints"; parameter SI.Diameter rodDiameter=1.1*cylinderDiameter "Diameter of the two rods connecting the revolute joints"; input Types.Color rodColor=Modelica.Mechanics.MultiBody.Types.Defaults.RodColor "Color of the two rods connecting the revolute joint"; input Types.SpecularCoefficient specularCoefficient = world.defaultSpecularCoefficient "Reflection of ambient light (= 0: light is completely absorbed)"; parameter Boolean checkTotalPower=false "= true, if total power flowing into this component shall be determined (must be zero)"; final parameter Real e_a[3](each final unit="1")=Modelica.Math.Vectors.normalize( n_a,0.0) "Unit vector along axes of rotations, resolved in frame_a"; final parameter Real e_ia[3](each final unit="1")=jointUSR.e2_ia "Unit vector along axes of rotations, resolved in frame_ia"; final parameter Real e_b[3](each final unit="1")=jointUSR.revolute.e "Unit vector along axes of rotations, resolved in frame_b, frame_ib and frame_im"; SI.Power totalPower=jointUSR.totalPower "Total power flowing into this element, if checkTotalPower=true (otherwise dummy)";JointUSR jointUSR( animation=false, n1_a=n_a, n_b=n_b, phi_offset=phi_offset, rRod2_ib=rRod2_ib, showUniversalAxes=false, rRod1_ia=rRod1_ia, checkTotalPower=checkTotalPower, phi_guess=phi_guess); protected Visualizers.Advanced.Shape shape_rev1( shapeType="cylinder", color=cylinderColor, specularCoefficient=specularCoefficient, length=cylinderLength, width=cylinderDiameter, height=cylinderDiameter, lengthDirection=e_a, widthDirection={0,1,0}, r_shape=-e_a*(cylinderLength/2), r=frame_a.r_0, R=frame_a.R) if world.enableAnimation and animation; Visualizers.Advanced.Shape shape_rev2( shapeType="cylinder", color=cylinderColor, specularCoefficient=specularCoefficient, length=cylinderLength, width=cylinderDiameter, height=cylinderDiameter, lengthDirection=e_b, widthDirection={0,1,0}, r_shape=-e_b*(cylinderLength/2), r=frame_im.r_0, R=frame_im.R) if world.enableAnimation and animation; Visualizers.Advanced.Shape shape_rev3( shapeType="cylinder", color=cylinderColor, specularCoefficient=specularCoefficient, length=cylinderLength, width=cylinderDiameter, height=cylinderDiameter, lengthDirection=e_b, widthDirection={0,1,0}, r_shape=-e_b*(cylinderLength/2), r=frame_b.r_0, R=frame_b.R) if world.enableAnimation and animation; Visualizers.Advanced.Shape shape_rod1( shapeType="cylinder", color=rodColor, specularCoefficient=specularCoefficient, length=Modelica.Math.Vectors.length( rRod1_ia), width=rodDiameter, height=rodDiameter, lengthDirection=rRod1_ia, widthDirection=e_ia, r=frame_ia.r_0, R=frame_ia.R) if world.enableAnimation and animation; Visualizers.Advanced.Shape shape_rod2( shapeType="cylinder", color=rodColor, specularCoefficient=specularCoefficient, length=Modelica.Math.Vectors.length( rRod2_ib), width=rodDiameter, height=rodDiameter, lengthDirection=rRod2_ib, widthDirection=e_b, r=frame_ib.r_0, R=frame_ib.R) if world.enableAnimation and animation; initial equation n_b = Frames.resolve2(frame_b.R, Frames.resolve1(frame_a.R, n_a)); equationconnect(jointUSR.frame_a, frame_a); connect(jointUSR.frame_b, frame_b); connect(jointUSR.frame_ia, frame_ia); connect(jointUSR.frame_im, frame_im); connect(jointUSR.frame_ib, frame_ib); connect(jointUSR.axis, axis); connect(jointUSR.bearing, bearing); end JointRRR;
 Modelica.Mechanics.MultiBody.Joints.Assemblies.JointRRP
Modelica.Mechanics.MultiBody.Joints.Assemblies.JointRRP
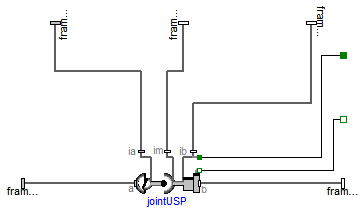
This component consists of 2 revolute joints with parallel axes of rotation that and a prismatic joint with a translational axis that is orthogonal to the revolute joint axes, see the default animation in the following figure (the axes vectors are not part of the default animation):

This joint aggregation introduces neither constraints nor state variables and should therefore be used in kinematic loops whenever possible to avoid non-linear systems of equations. It is only meaningful to use this component in planar loops. Basically, the position and orientation of the 3 joints as well as of frame_ia, frame_ib, and frame_im are calculated by solving analytically a non-linear equation, given the position and orientation at frame_a and at frame_b.
Connector frame_a is the "left" side of the first revolute joint whereas frame_ia is the "right side of this revolute joint, fixed in rod 1. Connector frame_b is the "right" side of the prismatic joint whereas frame_ib is the "left" side of this prismatic joint, fixed in rod 2. Finally, connector frame_im is the connector at the "right" side of the revolute joint in the middle, fixed in rod 2. The frames frame_b, frame_ib, frame_im are always parallel to each other.
The easiest way to define the parameters of this joint is by moving the MultiBody system in a reference configuration where all frames of all components are parallel to each other (alternatively, at least frame_a, frame_ia, frame_im, frame_ib, frame_b of the JointRRP joint should be parallel to each other when defining an instance of this component).
Basically, the JointRRP model consists internally of a universal - spherical - prismatic joint aggregation (= JointUSP). In a planar loop this will behave as if 2 revolute joints with parallel axes and 1 prismatic joint are connected by rigid rods.
Extends from Interfaces.PartialTwoFramesDoubleSize (Base model for components providing two frame connectors + outer world + assert to guarantee that the component is connected (default icon size is factor 2 larger as usual)).
| Type | Name | Default | Description |
|---|---|---|---|
| Boolean | animation | true | = true, if animation shall be enabled |
| Axis | n_a | {0,0,1} | Axes of the two revolute joints resolved in frame_a (both axes are parallel to each other) [1] |
| Axis | n_b | {-1,0,0} | Axis of prismatic joint fixed and resolved in frame_b (must be orthogonal to revolute joint axes) [1] |
| Position | rRod1_ia[3] | {1,0,0} | Vector from origin of frame_a to revolute joint in the middle, resolved in frame_ia [m] |
| Position | rRod2_ib[3] | {-1,0,0} | Vector from origin of frame_ib to revolute joint in the middle, resolved in frame_ib (frame_ib is parallel to frame_b) [m] |
| Position | s_offset | 0 | Relative distance offset of prismatic joint (distance between the prismatic joint frames = s(t) + s_offset) [m] |
| Position | s_guess | 0 | Select the configuration such that at initial time |s(t0)-s_guess|is minimal [m] |
| Animation | |||
| if animation = true | |||
| Distance | cylinderLength | world.defaultJointLength | Length of cylinders representing the revolute joints [m] |
| Distance | cylinderDiameter | world.defaultJointWidth | Diameter of cylinders representing the revolute joints [m] |
| Color | cylinderColor | Modelica.Mechanics.MultiBody... | Color of cylinders representing the revolute joints |
| Axis | boxWidthDirection | {0,1,0} | Vector in width direction of prismatic joint, resolved in frame_b [1] |
| Distance | boxWidth | world.defaultJointWidth | Width of prismatic joint box [m] |
| Distance | boxHeight | boxWidth | Height of prismatic joint box [m] |
| Color | boxColor | cylinderColor | Color of prismatic joint box |
| Diameter | rodDiameter | 1.1*cylinderDiameter | Diameter of the two rods connecting the joints [m] |
| Color | rodColor | Modelica.Mechanics.MultiBody... | Color of the two rods connecting the joints |
| SpecularCoefficient | specularCoefficient | world.defaultSpecularCoeffic... | Reflection of ambient light (= 0: light is completely absorbed) |
| Advanced | |||
| Boolean | checkTotalPower | false | = true, if total power flowing into this component shall be determined (must be zero) |
| Type | Name | Description |
|---|---|---|
| Frame_a | frame_a | Coordinate system fixed to the component with one cut-force and cut-torque |
| Frame_b | frame_b | Coordinate system fixed to the component with one cut-force and cut-torque |
| Frame_a | frame_ia | Coordinate system at origin of frame_a fixed at connecting rod of revolute joints |
| Frame_b | frame_ib | Coordinate system at origin of frame_b fixed at connecting rod of revolute and prismatic joint |
| Frame_b | frame_im | Coordinate system at origin of revolute joint in the middle fixed at connecting rod of revolute and prismatic joint |
| Flange_a | axis | 1-dim. translational flange that drives the prismatic joint |
| Flange_b | bearing | 1-dim. translational flange of the drive bearing of the prismatic joint |
model JointRRP "Planar revolute - revolute - prismatic joint aggregation (no constraints, no potential states)" import SI = Modelica.SIunits; import Cv = Modelica.SIunits.Conversions; import Modelica.Mechanics.MultiBody.Types; extends Interfaces.PartialTwoFramesDoubleSize;Modelica.Mechanics.MultiBody.Interfaces.Frame_a frame_ia "Coordinate system at origin of frame_a fixed at connecting rod of revolute joints"; Modelica.Mechanics.MultiBody.Interfaces.Frame_b frame_ib "Coordinate system at origin of frame_b fixed at connecting rod of revolute and prismatic joint"; Modelica.Mechanics.MultiBody.Interfaces.Frame_b frame_im "Coordinate system at origin of revolute joint in the middle fixed at connecting rod of revolute and prismatic joint"; Modelica.Mechanics.Translational.Interfaces.Flange_a axis "1-dim. translational flange that drives the prismatic joint"; Modelica.Mechanics.Translational.Interfaces.Flange_b bearing "1-dim. translational flange of the drive bearing of the prismatic joint"; parameter Boolean animation=true "= true, if animation shall be enabled"; parameter Modelica.Mechanics.MultiBody.Types.Axis n_a={0,0,1} "Axes of the two revolute joints resolved in frame_a (both axes are parallel to each other)"; parameter Modelica.Mechanics.MultiBody.Types.Axis n_b={-1,0,0} "Axis of prismatic joint fixed and resolved in frame_b (must be orthogonal to revolute joint axes)"; parameter SI.Position rRod1_ia[3]={1,0,0} "Vector from origin of frame_a to revolute joint in the middle, resolved in frame_ia"; parameter SI.Position rRod2_ib[3]={-1,0,0} "Vector from origin of frame_ib to revolute joint in the middle, resolved in frame_ib (frame_ib is parallel to frame_b)"; parameter SI.Position s_offset=0 "Relative distance offset of prismatic joint (distance between the prismatic joint frames = s(t) + s_offset)"; parameter SI.Position s_guess=0 "Select the configuration such that at initial time |s(t0)-s_guess|is minimal"; parameter SI.Distance cylinderLength=world.defaultJointLength "Length of cylinders representing the revolute joints"; parameter SI.Distance cylinderDiameter=world.defaultJointWidth "Diameter of cylinders representing the revolute joints"; input Types.Color cylinderColor=Modelica.Mechanics.MultiBody.Types.Defaults.JointColor "Color of cylinders representing the revolute joints"; parameter Types.Axis boxWidthDirection={0,1,0} "Vector in width direction of prismatic joint, resolved in frame_b"; parameter SI.Distance boxWidth=world.defaultJointWidth "Width of prismatic joint box"; parameter SI.Distance boxHeight=boxWidth "Height of prismatic joint box"; input Types.Color boxColor=cylinderColor "Color of prismatic joint box"; parameter SI.Diameter rodDiameter=1.1*cylinderDiameter "Diameter of the two rods connecting the joints"; input Types.Color rodColor=Modelica.Mechanics.MultiBody.Types.Defaults.RodColor "Color of the two rods connecting the joints"; input Types.SpecularCoefficient specularCoefficient = world.defaultSpecularCoefficient "Reflection of ambient light (= 0: light is completely absorbed)"; parameter Boolean checkTotalPower=false "= true, if total power flowing into this component shall be determined (must be zero)"; final parameter Real e_a[3](each final unit="1")=Modelica.Math.Vectors.normalize( n_a,0.0) "Unit vector along axes of rotations, resolved in frame_a"; final parameter Real e_ia[3](each final unit="1")=jointUSP.e2_ia "Unit vector along axes of rotations, resolved in frame_ia"; final parameter Real e_im[3](each final unit="1", each fixed=false) "Unit vector along axes of rotations, resolved in frame_im"; final parameter Real e_b[3](each final unit="1")=jointUSP.prismatic.e "Unit vector along axes of translation of the prismatic joint, resolved in frame_b and frame_ib"; SI.Power totalPower=jointUSP.totalPower "Total power flowing into this element, if checkTotalPower=true (otherwise dummy)";JointUSP jointUSP( animation=false, showUniversalAxes=false, n1_a=n_a, n_b=n_b, s_offset=s_offset, s_guess=s_guess, rRod1_ia=rRod1_ia, rRod2_ib=rRod2_ib, checkTotalPower=checkTotalPower); protected Visualizers.Advanced.Shape shape_rev1( shapeType="cylinder", color=cylinderColor, specularCoefficient=specularCoefficient, length=cylinderLength, width=cylinderDiameter, height=cylinderDiameter, lengthDirection=e_a, widthDirection={0,1,0}, r_shape=-e_a*(cylinderLength/2), r=frame_a.r_0, R=frame_a.R) if world.enableAnimation and animation; Visualizers.Advanced.Shape shape_rev2( shapeType="cylinder", color=cylinderColor, specularCoefficient=specularCoefficient, length=cylinderLength, width=cylinderDiameter, height=cylinderDiameter, lengthDirection=e_im, widthDirection={0,1,0}, r_shape=-e_im*(cylinderLength/2), r=frame_im.r_0, R=frame_im.R) if world.enableAnimation and animation; Visualizers.Advanced.Shape shape_prism( shapeType="box", color=boxColor, specularCoefficient=specularCoefficient, length=jointUSP.prismatic.distance, width=boxWidth, height=boxHeight, lengthDirection=e_b, widthDirection=e_im, r=frame_b.r_0, R=frame_b.R) if world.enableAnimation and animation; Visualizers.Advanced.Shape shape_rod1( shapeType="cylinder", color=rodColor, specularCoefficient=specularCoefficient, length=Modelica.Math.Vectors.length( rRod1_ia), width=rodDiameter, height=rodDiameter, lengthDirection=rRod1_ia, widthDirection=e_ia, r=frame_ia.r_0, R=frame_ia.R) if world.enableAnimation and animation; Visualizers.Advanced.Shape shape_rod2( shapeType="cylinder", color=rodColor, specularCoefficient=specularCoefficient, length=Modelica.Math.Vectors.length( rRod2_ib), width=rodDiameter, height=rodDiameter, lengthDirection=rRod2_ib, widthDirection=e_b, r=frame_ib.r_0, R=frame_ib.R) if world.enableAnimation and animation; initial equation e_im = Frames.resolve2(frame_im.R, Frames.resolve1(frame_a.R, e_a)); equationconnect(jointUSP.frame_a, frame_a); connect(jointUSP.frame_b, frame_b); connect(jointUSP.frame_ia, frame_ia); connect(jointUSP.frame_im, frame_im); connect(jointUSP.frame_ib, frame_ib); connect(jointUSP.axis, axis); connect(jointUSP.bearing, bearing); end JointRRP;