This package contains basic mathematical functions (such as sin(..)), as well as functions operating on vectors and matrices.
Copyright © 1998-2009, Modelica Association and DLR.
This Modelica package is free software; it can be redistributed and/or modified under the terms of the Modelica license, see the license conditions and the accompanying disclaimer here.
Extends from Modelica.Icons.Library2 (Icon for library where additional icon elements shall be added).
| Name | Description |
|---|---|
| Library of functions operating on vectors | |
| Library of functions operating on matrices | |
| Sine | |
| Cosine | |
| Tangent (u shall not be -pi/2, pi/2, 3*pi/2, ...) | |
| Inverse sine (-1 <= u <= 1) | |
| Inverse cosine (-1 <= u <= 1) | |
| Inverse tangent | |
| Four quadrant inverse tangent | |
| Four quadrant inverse tangens (select solution that is closest to given angle y0) | |
| Hyperbolic sine | |
| Hyperbolic cosine | |
| Hyperbolic tangent | |
| Inverse of sinh (area hyperbolic sine) | |
| Inverse of cosh (area hyperbolic cosine) | |
| Exponential, base e | |
| Natural (base e) logarithm (u shall be > 0) | |
| Base 10 logarithm (u shall be > 0) | |
| Basic icon for mathematical function with y-axis on left side | |
| Basic icon for mathematical function with y-axis in middle | |
| Temporary function for linear interpolation (will be removed) | |
| Temporary function for vectorized linear interpolation (will be removed) |
 Modelica.Math.sin
Modelica.Math.sin
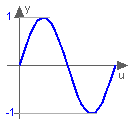
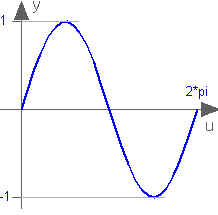
This function returns y = sin(u), with -∞ < u < ∞:
Extends from baseIcon1 (Basic icon for mathematical function with y-axis on left side).
| Type | Name | Default | Description |
|---|---|---|---|
| Angle | u | [rad] |
| Type | Name | Description |
|---|---|---|
| Real | y |
function sin "Sine" extends baseIcon1; input SI.Angle u; output Real y; external "C" y = sin(u);end sin;
 Modelica.Math.cos
Modelica.Math.cos
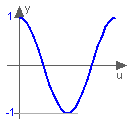
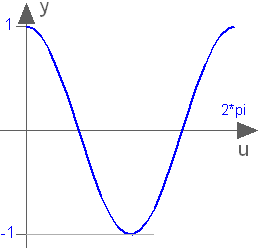
This function returns y = cos(u), with -∞ < u < ∞:
Extends from baseIcon1 (Basic icon for mathematical function with y-axis on left side).
| Type | Name | Default | Description |
|---|---|---|---|
| Angle | u | [rad] |
| Type | Name | Description |
|---|---|---|
| Real | y |
function cos "Cosine" extends baseIcon1; input SI.Angle u; output Real y; external "C" y = cos(u);end cos;
 Modelica.Math.tan
Modelica.Math.tan
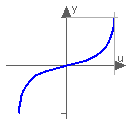
This function returns y = tan(u), with -∞ < u < ∞ (if u is a multiple of (2n-1)*pi/2, y = tan(u) is +/- infinity).
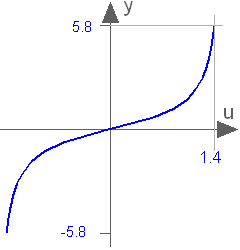
Extends from baseIcon2 (Basic icon for mathematical function with y-axis in middle).
| Type | Name | Default | Description |
|---|---|---|---|
| Angle | u | [rad] |
| Type | Name | Description |
|---|---|---|
| Real | y |
function tan "Tangent (u shall not be -pi/2, pi/2, 3*pi/2, ...)" extends baseIcon2; input SI.Angle u; output Real y; external "C" y = tan(u);end tan;
 Modelica.Math.asin
Modelica.Math.asin
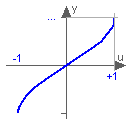
This function returns y = asin(u), with -1 ≤ u ≤ +1:
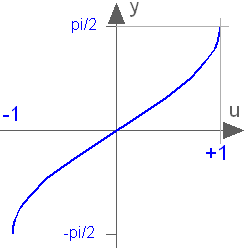
Extends from baseIcon2 (Basic icon for mathematical function with y-axis in middle).
| Type | Name | Default | Description |
|---|---|---|---|
| Real | u |
| Type | Name | Description |
|---|---|---|
| Angle | y | [rad] |
function asin "Inverse sine (-1 <= u <= 1)" extends baseIcon2; input Real u; output SI.Angle y; external "C" y = asin(u);end asin;
 Modelica.Math.acos
Modelica.Math.acos
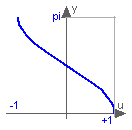
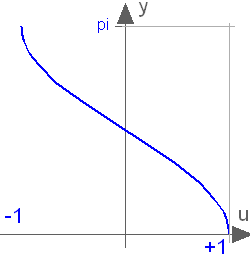
This function returns y = acos(u), with -1 ≤ u ≤ +1:
Extends from baseIcon2 (Basic icon for mathematical function with y-axis in middle).
| Type | Name | Default | Description |
|---|---|---|---|
| Real | u |
| Type | Name | Description |
|---|---|---|
| Angle | y | [rad] |
function acos "Inverse cosine (-1 <= u <= 1)" extends baseIcon2; input Real u; output SI.Angle y; external "C" y = acos(u);end acos;
 Modelica.Math.atan
Modelica.Math.atan
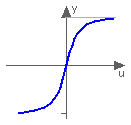
This function returns y = atan(u), with -∞ < u < ∞:
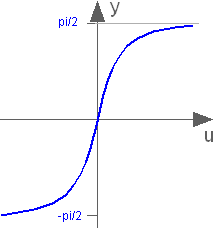
Extends from baseIcon2 (Basic icon for mathematical function with y-axis in middle).
| Type | Name | Default | Description |
|---|---|---|---|
| Real | u |
| Type | Name | Description |
|---|---|---|
| Angle | y | [rad] |
function atan "Inverse tangent" extends baseIcon2; input Real u; output SI.Angle y; external "C" y = atan(u);end atan;
 Modelica.Math.atan2
Modelica.Math.atan2
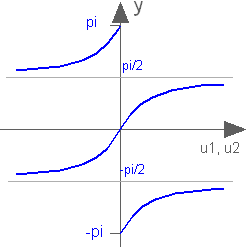
Extends from baseIcon2 (Basic icon for mathematical function with y-axis in middle).
| Type | Name | Default | Description |
|---|---|---|---|
| Real | u1 | ||
| Real | u2 |
| Type | Name | Description |
|---|---|---|
| Angle | y | [rad] |
function atan2 "Four quadrant inverse tangent" extends baseIcon2; input Real u1; input Real u2; output SI.Angle y; external "C" y = atan2(u1, u2);end atan2;
 Modelica.Math.atan3
Modelica.Math.atan3
This function returns y = atan3(u1,u2,y0) such that
tan(y) = u1/u2 and
y is in the range: -pi < y-y0 < pi.
u2 may be zero, provided u1 is not zero. The difference to
Modelica.Math.atan2(..) is the optional third argument y0 that
allows to specify which of the infinite many solutions
shall be returned:
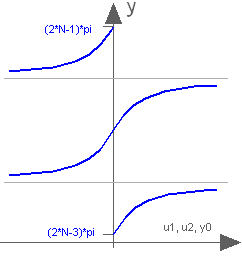
Extends from Modelica.Math.baseIcon2 (Basic icon for mathematical function with y-axis in middle).
| Type | Name | Default | Description |
|---|---|---|---|
| Real | u1 | ||
| Real | u2 | ||
| Angle | y0 | 0 | y shall be in the range: -pi < y-y0 < pi [rad] |
| Type | Name | Description |
|---|---|---|
| Angle | y | [rad] |
function atan3 "Four quadrant inverse tangens (select solution that is closest to given angle y0)" import Modelica.Math; extends Modelica.Math.baseIcon2; input Real u1; input Real u2; input Modelica.SIunits.Angle y0=0 "y shall be in the range: -pi < y-y0 < pi"; output Modelica.SIunits.Angle y; protected Real pi = Modelica.Constants.pi; Real w; algorithm w :=Math.atan2(u1, u2); y := w + 2*pi*div(abs(w-y0)+pi,2*pi)*(if y0 > w then +1 else -1);end atan3;
 Modelica.Math.sinh
Modelica.Math.sinh
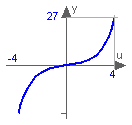
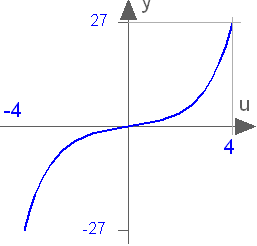
This function returns y = sinh(u), with -∞ < u < ∞:
Extends from baseIcon2 (Basic icon for mathematical function with y-axis in middle).
| Type | Name | Default | Description |
|---|---|---|---|
| Real | u |
| Type | Name | Description |
|---|---|---|
| Real | y |
function sinh "Hyperbolic sine" extends baseIcon2; input Real u; output Real y; external "C" y = sinh(u);end sinh;
 Modelica.Math.cosh
Modelica.Math.cosh
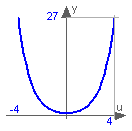
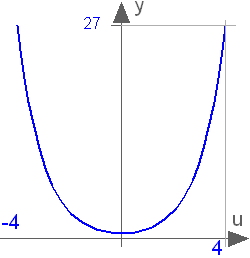
This function returns y = cosh(u), with -∞ < u < ∞:
Extends from baseIcon2 (Basic icon for mathematical function with y-axis in middle).
| Type | Name | Default | Description |
|---|---|---|---|
| Real | u |
| Type | Name | Description |
|---|---|---|
| Real | y |
function cosh "Hyperbolic cosine" extends baseIcon2; input Real u; output Real y; external "C" y = cosh(u);end cosh;
 Modelica.Math.tanh
Modelica.Math.tanh
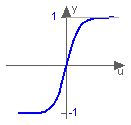
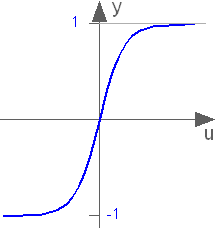
This function returns y = tanh(u), with -∞ < u < ∞:
Extends from baseIcon2 (Basic icon for mathematical function with y-axis in middle).
| Type | Name | Default | Description |
|---|---|---|---|
| Real | u |
| Type | Name | Description |
|---|---|---|
| Real | y |
function tanh "Hyperbolic tangent" extends baseIcon2; input Real u; output Real y; external "C" y = tanh(u);end tanh;
 Modelica.Math.asinh
Modelica.Math.asinh
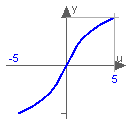
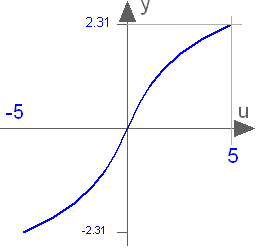
The function returns the area hyperbolic sine of its input argument u. This inverse of sinh(..) is unique and there is no restriction on the input argument u of asinh(u) (-∞ < u < ∞):
Extends from Modelica.Math.baseIcon2 (Basic icon for mathematical function with y-axis in middle).
| Type | Name | Default | Description |
|---|---|---|---|
| Real | u |
| Type | Name | Description |
|---|---|---|
| Real | y |
function asinh "Inverse of sinh (area hyperbolic sine)" extends Modelica.Math.baseIcon2; input Real u; output Real y; algorithm y :=Modelica.Math.log(u + sqrt(u*u + 1));end asinh;
 Modelica.Math.acosh
Modelica.Math.acosh
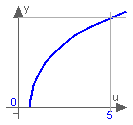
This function returns the area hyperbolic cosine of its input argument u. The valid range of u is
+1 ≤ u < +∞
If the function is called with u < 1, an error occurs. The function cosh(u) has two inverse functions (the curve looks similar to a sqrt(..) function). acosh(..) returns the inverse that is positive. At u=1, the derivative dy/du is infinite. Therefore, this function should not be used in a model, if u can become close to 1:
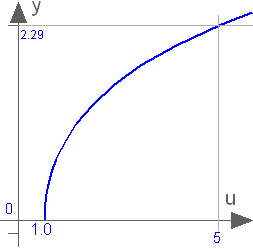
Extends from Modelica.Math.baseIcon1 (Basic icon for mathematical function with y-axis on left side).
| Type | Name | Default | Description |
|---|---|---|---|
| Real | u |
| Type | Name | Description |
|---|---|---|
| Real | y |
function acosh "Inverse of cosh (area hyperbolic cosine)" import Modelica.Utilities.Streams.*; extends Modelica.Math.baseIcon1; input Real u; output Real y; algorithm assert(u>=1.0, "Input argument u (= " + String(u) + ") of acosh(u) must be >= 1.0"); y :=Modelica.Math.log(u + sqrt(u*u - 1));end acosh;
 Modelica.Math.exp
Modelica.Math.exp
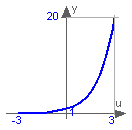
This function returns y = exp(u), with -∞ < u < ∞:
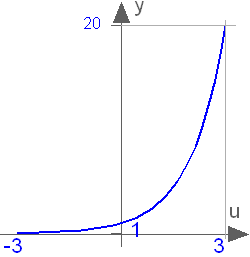
Extends from baseIcon2 (Basic icon for mathematical function with y-axis in middle).
| Type | Name | Default | Description |
|---|---|---|---|
| Real | u |
| Type | Name | Description |
|---|---|---|
| Real | y |
function exp "Exponential, base e" extends baseIcon2; input Real u; output Real y; external "C" y = exp(u);end exp;
 Modelica.Math.log
Modelica.Math.log
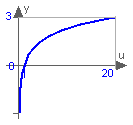
This function returns y = log(10) (the natural logarithm of u), with u > 0:
Extends from baseIcon1 (Basic icon for mathematical function with y-axis on left side).
| Type | Name | Default | Description |
|---|---|---|---|
| Real | u |
| Type | Name | Description |
|---|---|---|
| Real | y |
function log "Natural (base e) logarithm (u shall be > 0)" extends baseIcon1; input Real u; output Real y; external "C" y = log(u);end log;
 Modelica.Math.log10
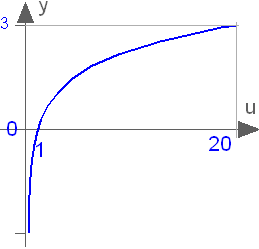
Modelica.Math.log10
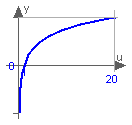
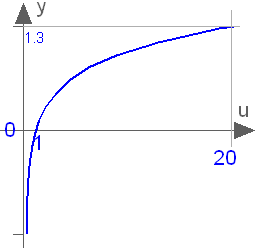
This function returns y = log10(u), with u > 0:
Extends from baseIcon1 (Basic icon for mathematical function with y-axis on left side).
| Type | Name | Default | Description |
|---|---|---|---|
| Real | u |
| Type | Name | Description |
|---|---|---|
| Real | y |
function log10 "Base 10 logarithm (u shall be > 0)" extends baseIcon1; input Real u; output Real y; external "C" y = log10(u);end log10;
![]()
Icon for a mathematical function, consisting of an y-axis on the left side. It is expected, that an x-axis is added and a plot of the function.
partial function baseIcon1 "Basic icon for mathematical function with y-axis on left side"end baseIcon1;
![]()
partial function baseIcon2 "Basic icon for mathematical function with y-axis in middle"end baseIcon2;
| Type | Name | Default | Description |
|---|---|---|---|
| Real | u | input value (first column of table) | |
| Real | table[:, :] | table to be interpolated | |
| Integer | icol | column of table to be interpolated |
| Type | Name | Description |
|---|---|---|
| Real | y | interpolated input value (icol column of table) |
function tempInterpol1
"Temporary function for linear interpolation (will be removed)"
input Real u "input value (first column of table)";
input Real table[:, :] "table to be interpolated";
input Integer icol "column of table to be interpolated";
output Real y "interpolated input value (icol column of table)";
protected
Integer i;
Integer n "number of rows of table";
Real u1;
Real u2;
Real y1;
Real y2;
algorithm
n := size(table, 1);
if n <= 1 then
y := table[1, icol];
else
// Search interval
if u <= table[1, 1] then
i := 1;
else
i := 2;
// Supports duplicate table[i, 1] values
// in the interior to allow discontinuities.
// Interior means that
// if table[i, 1] = table[i+1, 1] we require i>1 and i+1<n
while i < n and u >= table[i, 1] loop
i := i + 1;
end while;
i := i - 1;
end if;
// Get interpolation data
u1 := table[i, 1];
u2 := table[i + 1, 1];
y1 := table[i, icol];
y2 := table[i + 1, icol];
assert(u2 > u1, "Table index must be increasing");
// Interpolate
y := y1 + (y2 - y1)*(u - u1)/(u2 - u1);
end if;
end tempInterpol1;
| Type | Name | Default | Description |
|---|---|---|---|
| Real | u | input value (first column of table) | |
| Real | table[:, :] | table to be interpolated | |
| Integer | icol[:] | column(s) of table to be interpolated |
| Type | Name | Description |
|---|---|---|
| Real | y[1, size(icol, 1)] | interpolated input value(s) (column(s) icol of table) |
function tempInterpol2
"Temporary function for vectorized linear interpolation (will be removed)"
input Real u "input value (first column of table)";
input Real table[:, :] "table to be interpolated";
input Integer icol[:] "column(s) of table to be interpolated";
output Real y[1, size(icol, 1)]
"interpolated input value(s) (column(s) icol of table)";
protected
Integer i;
Integer n "number of rows of table";
Real u1;
Real u2;
Real y1[1, size(icol, 1)];
Real y2[1, size(icol, 1)];
algorithm
n := size(table, 1);
if n <= 1 then
y := transpose([table[1, icol]]);
else
// Search interval
if u <= table[1, 1] then
i := 1;
else
i := 2;
// Supports duplicate table[i, 1] values
// in the interior to allow discontinuities.
// Interior means that
// if table[i, 1] = table[i+1, 1] we require i>1 and i+1<n
while i < n and u >= table[i, 1] loop
i := i + 1;
end while;
i := i - 1;
end if;
// Get interpolation data
u1 := table[i, 1];
u2 := table[i + 1, 1];
y1 := transpose([table[i, icol]]);
y2 := transpose([table[i + 1, icol]]);
assert(u2 > u1, "Table index must be increasing");
// Interpolate
y := y1 + (y2 - y1)*(u - u1)/(u2 - u1);
end if;
end tempInterpol2;