This library provides functions operating on vectors:
| Function | Description |
|---|---|
| isEqual(v1, v2) | Determines whether two vectors have the same size and elements |
| norm(v,p) | p-norm of vector v |
| length(v) | Length of vector v (= norm(v,2), but inlined and therefore usable in symbolic manipulations) |
| normalize(v) | Return normalized vector such that length = 1 and prevent zero-division for zero vector |
| reverse(v) | Reverse vector elements |
| sort(v) | Sort elements of vector in ascending or descending order |
Extends from Modelica.Icons.Library (Icon for library).
| Name | Description |
|---|---|
| Determine if two Real vectors are numerically identical | |
| Return the p-norm of a vector | |
| Return length of a vectorReturn length of a vector (better as norm(), if further symbolic processing is performed) | |
| Return normalized vector such that length = 1Return normalized vector such that length = 1 and prevent zero-division for zero vector | |
| Reverse vector elements (e.g. v[1] becomes last element) | |
| Sort elements of vector in ascending or descending order |
 Modelica.Math.Vectors.isEqual
Modelica.Math.Vectors.isEqual
Vectors.isEqual(v1, v2); Vectors.isEqual(v1, v2, eps=0);
The function call "Vectors.isEqual(v1, v2)" returns true,
if the two Real vectors v1 and v2 have the same dimensions and
the same elements. Otherwise the function
returns false. Two elements e1 and e2 of the two vectors
are checked on equality by the test "abs(e1-e2) ≤ eps", where "eps"
can be provided as third argument of the function. Default is "eps = 0".
Real v1[3] = {1, 2, 3};
Real v2[3] = {1, 2, 3, 4};
Real v3[3] = {1, 2, 3.0001};
Boolean result;
algorithm
result := Vectors.isEqual(v1,v2); // = false
result := Vectors.isEqual(v1,v3); // = false
result := Vectors.isEqual(v1,v1); // = true
result := Vectors.isEqual(v1,v3,0.1); // = true
Extends from Modelica.Icons.Function (Icon for a function).
| Type | Name | Default | Description |
|---|---|---|---|
| Real | v1[:] | First vector | |
| Real | v2[:] | Second vector (may have different length as v1 | |
| Real | eps | 0 | Two elements e1 and e2 of the two vectors are identical if abs(e1-e2) <= eps |
| Type | Name | Description |
|---|---|---|
| Boolean | result | = true, if vectors have the same length and the same elements |
function isEqual
"Determine if two Real vectors are numerically identical"
extends Modelica.Icons.Function;
input Real v1[:] "First vector";
input Real v2[:] "Second vector (may have different length as v1";
input Real eps(min=0) = 0
"Two elements e1 and e2 of the two vectors are identical if abs(e1-e2) <= eps";
output Boolean result
"= true, if vectors have the same length and the same elements";
protected
Integer n=size(v1, 1) "Dimension of vector v1";
Integer i=1;
algorithm
result := false;
if size(v2, 1) == n then
result := true;
while i <= n loop
if abs(v1[i] - v2[i]) > eps then
result := false;
i := n;
end if;
i := i + 1;
end while;
end if;
end isEqual;
 Modelica.Math.Vectors.norm
Modelica.Math.Vectors.norm
Vectors.norm(v); Vectors.norm(v,p=2); // 1 ≤ p ≤ ∞
The function call "Vectors.norm(v)" returns the
Euclidean norm "sqrt(v*v)" of vector v.
With the optional
second argument "p", any other p-norm can be computed:
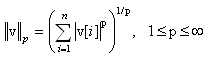
Besides the Euclidean norm (p=2), also the 1-norm and the infinity-norm are sometimes used:
| 1-norm | = sum(abs(v)) | norm(v,1) |
| 2-norm | = sqrt(v*v) | norm(v) or norm(v,2) |
| infinity-norm | = max(abs(v)) | norm(v,Modelica.Constants.inf) |
Note, for any vector norm the following inequality holds:
norm(v1+v2,p) ≤ norm(v1,p) + norm(v2,p)
v = {2, -4, -2, -1};
norm(v,1); // = 9
norm(v,2); // = 5
norm(v); // = 5
norm(v,10.5); // = 4.00052597412635
norm(v,Modelica.Constants.inf); // = 4
Extends from Modelica.Icons.Function (Icon for a function).
| Type | Name | Default | Description |
|---|---|---|---|
| Real | v[:] | Vector | |
| Real | p | 2 | Type of p-norm (often used: 1, 2, or Modelica.Constants.inf) |
| Type | Name | Description |
|---|---|---|
| Real | result | p-norm of vector v |
function norm "Return the p-norm of a vector"
extends Modelica.Icons.Function;
input Real v[:] "Vector";
input Real p(min=1) = 2
"Type of p-norm (often used: 1, 2, or Modelica.Constants.inf)";
output Real result "p-norm of vector v";
algorithm
if p == 2 then
result:=sqrt(v*v);
elseif p == Modelica.Constants.inf then
result:=max(abs(v));
elseif p == 1 then
result:=sum(abs(v));
else
result:=(sum(abs(v[i])^p for i in 1:size(v, 1)))^(1/p);
end if;
end norm;
 Modelica.Math.Vectors.length
Modelica.Math.Vectors.length
Vectors.length(v);
The function call "Vectors.length(v)" returns the
Euclidean length "sqrt(v*v)" of vector v.
The function call is equivalent to Vectors.norm(v). The advantage of
length(v) over norm(v)"is that function length(..) is implemented
in one statement and therefore the function is usually automatically
inlined. Further symbolic processing is therefore possible, which is
not the case with function norm(..).
v = {2, -4, -2, -1};
length(v); // = 5
Extends from Modelica.Icons.Function (Icon for a function).
| Type | Name | Default | Description |
|---|---|---|---|
| Real | v[:] | Vector |
| Type | Name | Description |
|---|---|---|
| Real | result | Length of vector v |
function length "Return length of a vectorReturn length of a vector (better as norm(), if further symbolic processing is performed)" extends Modelica.Icons.Function; input Real v[:] "Vector"; output Real result "Length of vector v"; algorithm result := sqrt(v*v);end length;
 Modelica.Math.Vectors.normalize
Modelica.Math.Vectors.normalize
Vectors.normalize(v); Vectors.normalize(v,eps=100*Modelica.Constants.eps);
The function call "Vectors.normalize(v)" returns the
unit vector "v/length(v)" of vector v.
If length(v) is close to zero (more precisely, if length(v) < eps),
v/eps is returned in order to avoid
a division by zero. For many applications this is useful, because
often the unit vector e = v/length(v) is used to compute
a vector x*e, where the scalar x is in the order of length(v),
i.e., x*e is small, when length(v) is small and then
it is fine to replace e by v to avoid a division by zero.
Since the function is implemented in one statement, it is usually inlined and therefore symbolic processing is possible.
normalize({1,2,3}); // = {0.267, 0.534, 0.802}
normalize({0,0,0}); // = {0,0,0}
Extends from Modelica.Icons.Function (Icon for a function).
| Type | Name | Default | Description |
|---|---|---|---|
| Real | v[:] | Vector | |
| Real | eps | 100*Modelica.Constants.eps | if |v| < eps then result = v/eps |
| Type | Name | Description |
|---|---|---|
| Real | result[size(v, 1)] | Input vector v normalized to length=1 |
function normalize
"Return normalized vector such that length = 1Return normalized vector such that length = 1 and prevent zero-division for zero vector"
extends Modelica.Icons.Function;
input Real v[:] "Vector";
input Real eps = 100*Modelica.Constants.eps
"if |v| < eps then result = v/eps";
output Real result[size(v, 1)] "Input vector v normalized to length=1";
algorithm
result := smooth(0,if length(v) >= eps then v/length(v) else v/eps);
end normalize;
 Modelica.Math.Vectors.reverse
Modelica.Math.Vectors.reverse
Vectors.reverse(v);
The function call "Vectors.reverse(v)" returns the
vector elements in reverse order.
reverse({1,2,3,4}); // = {4,3,2,1}
Extends from Modelica.Icons.Function (Icon for a function).
| Type | Name | Default | Description |
|---|---|---|---|
| Real | v[:] | Vector |
| Type | Name | Description |
|---|---|---|
| Real | result[size(v, 1)] | Elements of vector v in reversed order |
function reverse
"Reverse vector elements (e.g. v[1] becomes last element)"
extends Modelica.Icons.Function;
input Real v[:] "Vector";
output Real result[size(v, 1)] "Elements of vector v in reversed order";
algorithm
result := {v[end-i+1] for i in 1:size(v,1)};
end reverse;
 Modelica.Math.Vectors.sort
Modelica.Math.Vectors.sort
sorted_v = Vectors.sort(v);
(sorted_v, indices) = Vectors.sort(v, ascending=true);
Function sort(..) sorts a Real vector v in ascending order and returns the result in sorted_v. If the optional argument "ascending" is false, the vector is sorted in descending order. In the optional second output argument the indices of the sorted vector with respect to the original vector are given, such that sorted_v = v[indices].
(v2, i2) := Vectors.sort({-1, 8, 3, 6, 2});
-> v2 = {-1, 2, 3, 6, 8}
i2 = {1, 5, 3, 4, 2}
Extends from Modelica.Icons.Function (Icon for a function).
| Type | Name | Default | Description |
|---|---|---|---|
| Real | v[:] | Vector to be sorted | |
| Boolean | ascending | true | = true if ascending order, otherwise descending order |
| Type | Name | Description |
|---|---|---|
| Real | sorted_v[size(v, 1)] | Sorted vector |
| Integer | indices[size(v, 1)] | sorted_v = v[indices] |
function sort
"Sort elements of vector in ascending or descending order"
extends Modelica.Icons.Function;
input Real v[:] "Vector to be sorted";
input Boolean ascending = true
"= true if ascending order, otherwise descending order";
output Real sorted_v[size(v,1)] = v "Sorted vector";
output Integer indices[size(v,1)] = 1:size(v,1) "sorted_v = v[indices]";
/* shellsort algorithm; should be improved later */
protected
Integer gap;
Integer i;
Integer j;
Real wv;
Integer wi;
Integer nv = size(v,1);
Boolean swap;
algorithm
gap := div(nv,2);
while gap > 0 loop
i := gap;
while i < nv loop
j := i-gap;
if j>=0 then
if ascending then
swap := sorted_v[j+1] > sorted_v[j + gap + 1];
else
swap := sorted_v[j+1] < sorted_v[j + gap + 1];
end if;
else
swap := false;
end if;
while swap loop
wv := sorted_v[j+1];
wi := indices[j+1];
sorted_v[j+1] := sorted_v[j+gap+1];
sorted_v[j+gap+1] := wv;
indices[j+1] := indices[j+gap+1];
indices[j+gap+1] := wi;
j := j - gap;
if j >= 0 then
if ascending then
swap := sorted_v[j+1] > sorted_v[j + gap + 1];
else
swap := sorted_v[j+1] < sorted_v[j + gap + 1];
end if;
else
swap := false;
end if;
end while;
i := i + 1;
end while;
gap := div(gap,2);
end while;
end sort;