Modelica.Thermal.HeatTransfer.Examples

Information

Extends from Modelica.Icons.ExamplesPackage (Icon for packages containing runnable examples).

Package Content

Name	Description
TwoMasses	Simple conduction demo
ControlledTemperature	Control temperature of a resistor
Motor	Second order thermal model of a motor

Modelica.Thermal.HeatTransfer.Examples.TwoMasses

Information

This example demonstrates the thermal response of two masses connected by a conducting element. The two masses have the same heat capacity but different initial temperatures (T1=100 [degC], T2= 0 [degC]). The mass with the higher temperature will cool off while the mass with the lower temperature heats up. They will each asymptotically approach the calculated temperature T_final_K (T_final_degC) that results from dividing the total initial energy in the system by the sum of the heat capacities of each element.

Simulate for 5 s and plot the variables
mass1.T, mass2.T, T_final_K or
Tsensor1.T, Tsensor2.T, T_final_degC

Extends from Modelica.Icons.Example (Icon for runnable examples).

Parameters

Type	Name	Default	Description
Temperature	T_final_K		Projected final temperature [K]

Modelica definition

model TwoMasses "Simple conduction demo"
  extends Modelica.Icons.Example;
  parameter Modelica.SIunits.Temperature T_final_K(fixed=false) 
    "Projected final temperature";
  HeatTransfer.Components.HeatCapacitor mass1(
                                   C=15, T(start=373.15, fixed=true));
  HeatTransfer.Components.HeatCapacitor mass2(
                                   C=15, T(start=273.15, fixed=true));
  HeatTransfer.Components.ThermalConductor conduction(
                                           G=10);
  HeatTransfer.Celsius.TemperatureSensor Tsensor1;
  HeatTransfer.Celsius.TemperatureSensor Tsensor2;
equation 
  connect(mass1.port, conduction.port_a);
  connect(conduction.port_b, mass2.port);
  connect(mass1.port, Tsensor1.port);
  connect(mass2.port, Tsensor2.port);
initial equation 
  T_final_K = (mass1.T*mass1.C + mass2.T*mass2.C)/(mass1.C + mass2.C);
end TwoMasses;

Modelica.Thermal.HeatTransfer.Examples.ControlledTemperature

Information

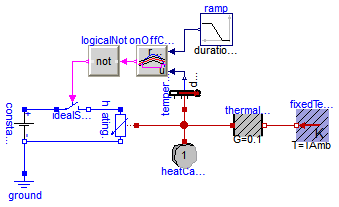
A constant voltage of 10 V is applied to a temperature dependent resistor of 10*(1+(T-20C)/(235+20C)) Ohms, whose losses v**2/r are dissipated via a thermal conductance of 0.1 W/K to ambient temperature 20 degree C. The resistor is assumed to have a thermal capacity of 1 J/K, having ambient temparature at the beginning of the experiment. The temperature of this heating resistor is held by an OnOff-controller at reference temperature within a given bandwith +/- 1 K by switching on and off the voltage source. The reference temperature starts at 25 degree C and rises between t = 2 and 8 seconds linear to 50 degree C. An approppriate simulating time would be 10 seconds.

Extends from Modelica.Icons.Example (Icon for runnable examples).

Parameters

Type	Name	Default	Description
Temperature	TAmb	293.15	Ambient Temperature [K]
TemperatureDifference	TDif	2	Error in Temperature [K]

Modelica definition

model ControlledTemperature "Control temperature of a resistor"
  extends Modelica.Icons.Example;
  parameter Modelica.SIunits.Temperature TAmb(displayUnit="degC") = 293.15 
    "Ambient Temperature";
  parameter Modelica.SIunits.TemperatureDifference TDif = 2 
    "Error in Temperature";
  output Modelica.SIunits.Temperature TRes(displayUnit="degC") = heatingResistor.heatPort.T 
    "Resulting Temperature";
  Modelica.Electrical.Analog.Basic.Ground ground;
  Modelica.Electrical.Analog.Sources.ConstantVoltage constantVoltage(V=10);
  HeatTransfer.Components.HeatCapacitor heatCapacitor(
                                           C=1, T(start=TAmb, fixed=true));
  Modelica.Electrical.Analog.Basic.HeatingResistor heatingResistor(
    R_ref=10,
    T_ref=from_degC(20),
    alpha=1/(235 + 20));
  HeatTransfer.Sources.FixedTemperature fixedTemperature(
                                                 T=TAmb);
  HeatTransfer.Celsius.TemperatureSensor temperatureSensor;
  HeatTransfer.Components.ThermalConductor thermalConductor(
                                                 G=0.1);
  Modelica.Electrical.Analog.Ideal.IdealOpeningSwitch idealSwitch;
  Modelica.Blocks.Sources.Ramp ramp(
    height=25,
    duration=6,
    offset=25,
    startTime=2);
  Modelica.Blocks.Logical.OnOffController onOffController(bandwidth=TDif);
  Modelica.Blocks.Logical.Not logicalNot;
equation 
  connect(constantVoltage.n, heatingResistor.n);
  connect(constantVoltage.n, ground.p);
  connect(heatingResistor.heatPort, thermalConductor.port_a);
  connect(thermalConductor.port_b, fixedTemperature.port);
  connect(heatingResistor.heatPort, temperatureSensor.port);
  connect(heatingResistor.heatPort, heatCapacitor.port);
  connect(constantVoltage.p, idealSwitch.p);
  connect(idealSwitch.n, heatingResistor.p);
  connect(ramp.y, onOffController.reference);
  connect(temperatureSensor.T, onOffController.u);
  connect(onOffController.y, logicalNot.u);
  connect(logicalNot.y, idealSwitch.control);
end ControlledTemperature;

Modelica.Thermal.HeatTransfer.Examples.Motor

Information

This example contains a simple second order thermal model of a motor. The periodic power losses are described by table "lossTable":

time	winding losses	core losses
0	100	500
360	100	500
360	1000	500
600	1000	500

Since constant speed is assumed, the core losses keep constant whereas the winding losses are low for 6 minutes (no-load) and high for 4 minutes (over load).
The winding losses are corrected by (1 + alpha*(T - T_ref)) because the winding's resistance is temperature dependent whereas the core losses are kept constant (alpha = 0).

The power dissipation to the environment is approximated by heat flow through a thermal conductance between winding and core, partially storage of the heat in the winding's heat capacity as well as the core's heat capacity and finally by forced convection to the environment.
Since constant speed is assumed, the cinvective conductance keeps constant.
Using Modelica.Thermal.FluidHeatFlow it would be possible to model the coolant air flow, too (instead of simple dissipation to a constant ambient's temperature).

Simulate for 7200 s; plot Twinding.T and Tcore.T.

Extends from Modelica.Icons.Example (Icon for runnable examples).

Parameters

Type	Name	Default	Description
Temperature	TAmb	293.15	Ambient temperature [K]

Modelica definition

model Motor "Second order thermal model of a motor"
  extends Modelica.Icons.Example;
  parameter Modelica.SIunits.Temperature TAmb(displayUnit="degC") = 293.15 
    "Ambient temperature";

  Modelica.Blocks.Sources.CombiTimeTable lossTable(extrapolation=Modelica.
        Blocks.Types.Extrapolation.Periodic, table=[0,100,500; 360,100,500;
        360,1000,500; 600,1000,500]);
  HeatTransfer.Sources.PrescribedHeatFlow windingLosses(
                                                T_ref=from_degC(95), alpha=
        3.03E-3);
  HeatTransfer.Components.HeatCapacitor winding(               C=2500, T(start=
          TAmb, fixed=true));
  HeatTransfer.Celsius.TemperatureSensor Twinding;
  HeatTransfer.Components.ThermalConductor winding2core(
                                             G=10);
  HeatTransfer.Sources.PrescribedHeatFlow coreLosses;
  HeatTransfer.Components.HeatCapacitor core(               C=25000, T(start=
          TAmb, fixed=true));
  HeatTransfer.Celsius.TemperatureSensor Tcore;
  Modelica.Blocks.Sources.Constant convectionConstant(k=25);
  HeatTransfer.Components.Convection convection;
  HeatTransfer.Sources.FixedTemperature environment(
                                            T=TAmb);
equation 
  connect(windingLosses.port, winding.port);
  connect(coreLosses.port, core.port);
  connect(winding.port, winding2core.port_a);
  connect(winding2core.port_b, core.port);
  connect(winding.port, Twinding.port);
  connect(core.port, Tcore.port);
  connect(winding2core.port_b, convection.solid);
  connect(convection.fluid, environment.port);
  connect(convectionConstant.y, convection.Gc);
  connect(lossTable.y[1], windingLosses.Q_flow);
  connect(lossTable.y[2], coreLosses.Q_flow);
end Motor;