Modelica.Mechanics.Rotational.Examples

Information

This package contains example models to demonstrate the usage of the Modelica.Mechanics.Rotational package. Open the models and simulate them according to the provided description in the models.

Extends from Modelica.Icons.Library (Icon for library).

Package Content

Name	Description
First	First example: simple drive train
FirstGrounded	First example: simple drive train with grounded elments
Friction	Drive train with clutch and brake
CoupledClutches	Drive train with 3 dynamically coupled clutches
LossyGearDemo1	Example to show that gear efficiency may lead to stuck motion
LossyGearDemo2	Example to show combination of LossyGear and BearingFriction
ElasticBearing	Example to show possible usage of support flange
Backlash	Example to demonstrate backlash
RollingWheel	Demonstrate coupling Rotational - Translational

Modelica.Mechanics.Rotational.Examples.First

Information

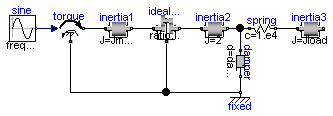
The drive train consists of a motor inertia which is driven by a sine-wave motor torque. Via a gearbox the rotational energy is transmitted to a load inertia. Elasticity in the gearbox is modeled by a spring element. A linear damper is used to model the damping in the gearbox bearing.

Note, that a force component (like the damper of this example) which is acting between a shaft and the housing has to be fixed in the housing on one side via component Fixed.

Simulate for 1 second and plot the following variables:
angular velocities of inertias inertia2 and 3: inertia2.w, inertia3.w

Extends from Modelica.Icons.Example (Icon for an example model).

Parameters

Type	Name	Default	Description
Torque	amplitude	10	Amplitude of driving torque [N.m]
Frequency	freqHz	5	Frequency of driving torque [Hz]
Inertia	Jmotor	0.1	Motor inertia [kg.m2]
Inertia	Jload	2	Load inertia [kg.m2]
Real	ratio	10	Gear ratio
Real	damping	10	Damping in bearing of gear

Modelica definition

model First "First example: simple drive train"
  import SI = Modelica.SIunits;

  extends Modelica.Icons.Example;

  parameter Modelica.SIunits.Torque amplitude=10 "Amplitude of driving torque";
  parameter SI.Frequency freqHz=5 "Frequency of driving torque";
  parameter SI.Inertia Jmotor(min=0)=0.1 "Motor inertia";
  parameter SI.Inertia Jload(min=0)=2 "Load inertia";
  parameter Real ratio=10 "Gear ratio";
  parameter Real damping=10 "Damping in bearing of gear";

  Rotational.Components.Fixed fixed;
  Rotational.Sources.Torque torque(useSupport=true);
  Rotational.Components.Inertia inertia1(        J=Jmotor);
  Rotational.Components.IdealGear idealGear(        ratio=ratio, useSupport=
       true);
  Rotational.Components.Inertia inertia2(        J=2,
    phi(fixed=true, start=0),
    w(fixed=true));
  Rotational.Components.Spring spring(        c=1.e4,
    phi_rel(fixed=true));
  Rotational.Components.Inertia inertia3(        J=Jload, w(fixed=true));
  Rotational.Components.Damper damper(        d=damping);
  Modelica.Blocks.Sources.Sine sine(amplitude=amplitude, freqHz=freqHz);
equation 
  connect(inertia1.flange_b, idealGear.flange_a);
  connect(idealGear.flange_b, inertia2.flange_a);
  connect(inertia2.flange_b, spring.flange_a);
  connect(spring.flange_b, inertia3.flange_a);
  connect(damper.flange_a, inertia2.flange_b);
  connect(damper.flange_b, fixed.flange);
  connect(sine.y, torque.tau);
  connect(torque.support, fixed.flange);
  connect(idealGear.support, fixed.flange);
  connect(torque.flange, inertia1.flange_a);
end First;

Modelica.Mechanics.Rotational.Examples.FirstGrounded

Information

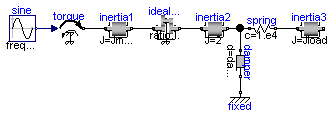
The drive train consists of a motor inertia which is driven by a sine-wave motor torque. Via a gearbox the rotational energy is transmitted to a load inertia. Elasticity in the gearbox is modeled by a spring element. A linear damper is used to model the damping in the gearbox bearing.

Note, that a force component (like the damper of this example) which is acting between a shaft and the housing has to be fixed in the housing on one side via component Fixed.

Simulate for 1 second and plot the following variables:
angular velocities of inertias inertia2 and 3: inertia2.w, inertia3.w

Extends from Modelica.Icons.Example (Icon for an example model).

Parameters

Type	Name	Default	Description
Torque	amplitude	10	Amplitude of driving torque [N.m]
Frequency	freqHz	5	Frequency of driving torque [Hz]
Inertia	Jmotor	0.1	Motor inertia [kg.m2]
Inertia	Jload	2	Load inertia [kg.m2]
Real	ratio	10	Gear ratio
Real	damping	10	Damping in bearing of gear

Modelica definition

model FirstGrounded 
  "First example: simple drive train with grounded elments"
  import SI = Modelica.SIunits;

  extends Modelica.Icons.Example;

  parameter Modelica.SIunits.Torque amplitude=10 "Amplitude of driving torque";
  parameter SI.Frequency freqHz=5 "Frequency of driving torque";
  parameter SI.Inertia Jmotor(min=0)=0.1 "Motor inertia";
  parameter SI.Inertia Jload(min=0)=2 "Load inertia";
  parameter Real ratio=10 "Gear ratio";
  parameter Real damping=10 "Damping in bearing of gear";

  Rotational.Components.Fixed fixed;
  Rotational.Sources.Torque torque(useSupport=false);
  Rotational.Components.Inertia inertia1(        J=Jmotor);
  Rotational.Components.IdealGear idealGear(ratio=ratio, useSupport=false);
  Rotational.Components.Inertia inertia2(        J=2,
    phi(fixed=true, start=0),
    w(fixed=true));
  Rotational.Components.Spring spring(        c=1.e4,
    phi_rel(fixed=true));
  Rotational.Components.Inertia inertia3(        J=Jload, w(fixed=true));
  Rotational.Components.Damper damper(        d=damping);
  Modelica.Blocks.Sources.Sine sine(amplitude=amplitude, freqHz=freqHz);
equation 
  connect(inertia1.flange_b, idealGear.flange_a);
  connect(idealGear.flange_b, inertia2.flange_a);
  connect(inertia2.flange_b, spring.flange_a);
  connect(spring.flange_b, inertia3.flange_a);
  connect(damper.flange_a, inertia2.flange_b);
  connect(damper.flange_b, fixed.flange);
  connect(sine.y, torque.tau);
  connect(torque.flange, inertia1.flange_a);
end FirstGrounded;

Modelica.Mechanics.Rotational.Examples.Friction

Information

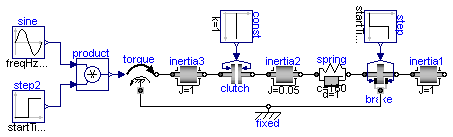
This drive train contains a frictional clutch and a brake. Simulate the system for 1 second using the following initial values (defined already in the model):

   inertia1.w =  90 (or brake.w)
   inertia2.w =  90
   inertia3.w = 100

Plot the output signals

   tMotor      Torque of motor
   tClutch     Torque in clutch
   tBrake      Torque in brake
   tSpring     Torque in spring

as well as the absolute angular velocities of the three inertia components (inertia1.w, inertia2.w, inertia3.w).

Extends from Modelica.Icons.Example (Icon for an example model).

Parameters

Type	Name	Default	Description
Time	startTime	0.5	Start time of step [s]

Modelica definition

model Friction "Drive train with clutch and brake"
  import Modelica.Constants.pi;
  import SI = Modelica.SIunits;

  extends Modelica.Icons.Example;

  parameter SI.Time startTime=0.5 "Start time of step";

  output SI.Torque tMotor "driving torque of inertia3";
  output SI.Torque tClutch "friction torque of clutch";
  output SI.Torque tBrake "friction torque of brake";
  output SI.Torque tSpring "spring torque";

  Rotational.Sources.Torque torque(useSupport=true);
  Rotational.Components.Inertia inertia3(
    J=1,
    phi(
      start=0,
      fixed=true,
      displayUnit="deg"),
    w(start=100,
      fixed=true,
      displayUnit="rad/s"));
  Rotational.Components.Clutch clutch(        fn_max=160);
  Rotational.Components.Inertia inertia2(
    J=0.05,
    phi(start=0, fixed=true),
    w(start=90, fixed=true));
  Rotational.Components.SpringDamper spring(        c=160, d=1);
  Rotational.Components.Inertia inertia1(
    J=1,
    phi(start=0, fixed=true),
    w(start=90, fixed=true));
  Rotational.Components.Brake brake(        fn_max=1600, useSupport=true);
  Modelica.Blocks.Sources.Constant const(k=1);
  Modelica.Blocks.Sources.Step step(startTime=startTime);
  Modelica.Blocks.Sources.Step step2(
    height=-1,
    offset=1,
    startTime=startTime);
  Modelica.Blocks.Sources.Sine sine(amplitude=200, freqHz=50/pi);
  Modelica.Blocks.Math.Product product;
  Rotational.Components.Fixed fixed;
equation 
  tMotor = torque.tau;
  tClutch = clutch.tau;
  tBrake = brake.tau;
  tSpring = spring.tau;

  connect(torque.flange, inertia3.flange_a);
  connect(inertia3.flange_b, clutch.flange_a);
  connect(clutch.flange_b, inertia2.flange_a);
  connect(inertia2.flange_b, spring.flange_a);
  connect(spring.flange_b, brake.flange_a);
  connect(brake.flange_b, inertia1.flange_a);
  connect(sine.y, product.u1);
  connect(step2.y, product.u2);
  connect(product.y, torque.tau);
  connect(const.y, clutch.f_normalized);
  connect(step.y, brake.f_normalized);
  connect(torque.support, fixed.flange);
  connect(brake.support, fixed.flange);
end Friction;

Modelica.Mechanics.Rotational.Examples.CoupledClutches

Information

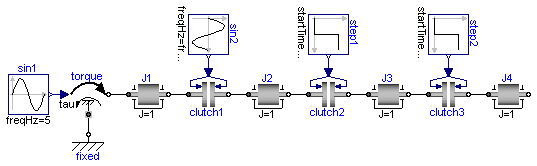
This example demonstrates how variable structure drive trains are handeled. The drive train consists of 4 inertias and 3 clutches, where the clutches are controlled by input signals. The system has 2^3=8 different configurations and 3^3 = 27 different states (every clutch may be in forward sliding, backward sliding or locked mode when the relative angular velocity is zero). By invoking the clutches at different time instances, the switching of the configurations can be studied.

Simulate the system for 1.2 seconds with the following initial values:
J1.w = 10.

Plot the following variables:
angular velocities of inertias (J1.w, J2.w, J3.w, J4.w), frictional torques of clutches (clutchX.tau), frictional mode of clutches (clutchX.mode) where mode = -1/0/+1 means backward sliding, locked, forward sliding.

Extends from Modelica.Icons.Example (Icon for an example model).

Parameters

Type	Name	Default	Description
Frequency	freqHz	0.2	frequency of sine function to invoke clutch1 [Hz]
Time	T2	0.4	time when clutch2 is invoked [s]
Time	T3	0.9	time when clutch3 is invoked [s]

Modelica definition

model CoupledClutches 
  "Drive train with 3 dynamically coupled clutches"

  import SI = Modelica.SIunits;

  extends Modelica.Icons.Example;

  parameter SI.Frequency freqHz=0.2 
    "frequency of sine function to invoke clutch1";
  parameter SI.Time T2=0.4 "time when clutch2 is invoked";
  parameter SI.Time T3=0.9 "time when clutch3 is invoked";

  Rotational.Components.Inertia J1(
    J=1,
    phi(fixed=true, start=0),
    w(start=10, fixed=true));
  Rotational.Sources.Torque torque(useSupport=true);
  Rotational.Components.Clutch clutch1(        peak=1.1, fn_max=20);
  Modelica.Blocks.Sources.Sine sin1(amplitude=10, freqHz=5);
  Modelica.Blocks.Sources.Step step1(startTime=T2);
  Rotational.Components.Inertia J2(        J=1,
    phi(fixed=true, start=0),
    w(fixed=true));
  Rotational.Components.Clutch clutch2(        peak=1.1, fn_max=20);
  Rotational.Components.Inertia J3(        J=1,
    phi(fixed=true, start=0),
    w(fixed=true));
  Rotational.Components.Clutch clutch3(        peak=1.1, fn_max=20);
  Rotational.Components.Inertia J4(        J=1,
    phi(fixed=true, start=0),
    w(fixed=true));
  Modelica.Blocks.Sources.Sine sin2(
    amplitude=1,
    freqHz=freqHz,
    phase=1.57);
  Modelica.Blocks.Sources.Step step2(startTime=T3);
  Rotational.Components.Fixed fixed;
equation 
  connect(torque.flange, J1.flange_a);
  connect(J1.flange_b, clutch1.flange_a);
  connect(clutch1.flange_b, J2.flange_a);
  connect(J2.flange_b, clutch2.flange_a);
  connect(clutch2.flange_b, J3.flange_a);
  connect(J3.flange_b, clutch3.flange_a);
  connect(clutch3.flange_b, J4.flange_a);
  connect(sin1.y, torque.tau);
  connect(sin2.y, clutch1.f_normalized);
  connect(step1.y, clutch2.f_normalized);
  connect(step2.y, clutch3.f_normalized);
  connect(fixed.flange, torque.support);
end CoupledClutches;

Modelica.Mechanics.Rotational.Examples.LossyGearDemo1

Information

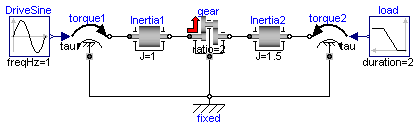
This model contains two inertias which are connected by an ideal gear where the friction between the teeth of the gear is modeled in a physical meaningful way (friction may lead to stuck mode which locks the motion of the gear). The friction is defined by an efficiency factor (= 0.5) for forward and backward driving condition leading to a torque dependent friction loss. Simulate for about 0.5 seconds. The friction in the gear will take all modes (forward and backward rolling, as well as stuck).

You may plot:

Inertia1.w,
Inertia2.w : angular velocities of inertias
powerLoss  : power lost in the gear
gear.mode  :  1 = forward rolling
              0 = stuck (w=0)
             -1 = backward rolling

Extends from Modelica.Icons.Example (Icon for an example model).

Modelica definition

model LossyGearDemo1 
  "Example to show that gear efficiency may lead to stuck motion"

  import SI = Modelica.SIunits;

  extends Modelica.Icons.Example;
  SI.Power PowerLoss "power lost in the gear";
  Rotational.Components.LossyGear gear(ratio=2, lossTable=[0, 0.5, 0.5, 0, 0],
    useSupport=true);
  Rotational.Components.Inertia Inertia1(J=1);
  Rotational.Components.Inertia Inertia2(        J=1.5,
    phi(fixed=true, start=0),
    w(fixed=true));
  Rotational.Sources.Torque torque1(useSupport=true);
  Rotational.Sources.Torque torque2(useSupport=true);
  Modelica.Blocks.Sources.Sine DriveSine(amplitude=10, freqHz=1);
  Modelica.Blocks.Sources.Ramp load(
    height=5,
    duration=2,
    offset=-10);
  Rotational.Components.Fixed fixed;
equation 
  connect(Inertia1.flange_b, gear.flange_a);
  connect(gear.flange_b, Inertia2.flange_a);
  connect(torque1.flange, Inertia1.flange_a);
  connect(torque2.flange, Inertia2.flange_b);
  PowerLoss = gear.flange_a.tau*der(gear.flange_a.phi) + gear.flange_b.tau*
    der(gear.flange_b.phi);

  connect(DriveSine.y, torque1.tau);
  connect(load.y, torque2.tau);
  connect(fixed.flange, gear.support);
  connect(fixed.flange, torque1.support);
  connect(fixed.flange, torque2.support);
end LossyGearDemo1;

Modelica.Mechanics.Rotational.Examples.LossyGearDemo2

Information

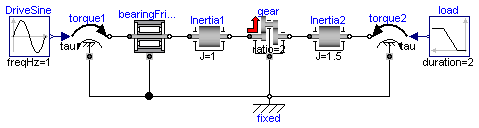
This model contains bearing friction and gear friction (= efficiency). If both friction models are stuck, there is no unique solution. Still a reliable Modelica simulator, such as Dymola, should be able to handle this situation.

Simulate for about 0.5 seconds. The friction elements are in all modes (forward and backward rolling, as well as stuck).

You may plot:

Inertia1.w,
Inertia2.w          : angular velocities of inertias
powerLoss           : power lost in the gear
bearingFriction.mode:  1 = forward rolling
                       0 = stuck (w=0)
                      -1 = backward rolling
gear.mode           :  1 = forward rolling
                       0 = stuck (w=0)
                      -1 = backward rolling

Note: This combination of LossyGear and BearingFriction is not recommended to use, as component LossyGear includes the functionality of component BearingFriction (only peak not supported).

Extends from Modelica.Icons.Example (Icon for an example model).

Modelica definition

model LossyGearDemo2 
  "Example to show combination of LossyGear and BearingFriction"

  import SI = Modelica.SIunits;

  extends Modelica.Icons.Example;
  SI.Power PowerLoss "power lost in the gear";

  Rotational.Components.LossyGear gear(ratio=2, lossTable=[0, 0.5, 0.5, 0, 0],
    useSupport=true);
  Rotational.Components.Inertia Inertia1(J=1);
  Rotational.Components.Inertia Inertia2(        J=1.5,
    phi(fixed=true, start=0),
    w(fixed=true));
  Rotational.Sources.Torque torque1(useSupport=true);
  Rotational.Sources.Torque torque2(useSupport=true);
  Modelica.Blocks.Sources.Sine DriveSine(amplitude=10, freqHz=1);
  Modelica.Blocks.Sources.Ramp load(
    height=5,
    duration=2,
    offset=-10);
  Rotational.Components.BearingFriction bearingFriction(        tau_pos=[0, 0.5; 1, 1],
      useSupport=true);
  Rotational.Components.Fixed fixed;
equation 
  PowerLoss = gear.flange_a.tau*der(gear.flange_a.phi) + gear.flange_b.tau*
    der(gear.flange_b.phi);
  connect(torque2.flange, Inertia2.flange_b);
  connect(Inertia2.flange_a, gear.flange_b);
  connect(gear.flange_a, Inertia1.flange_b);
  connect(Inertia1.flange_a, bearingFriction.flange_b);
  connect(bearingFriction.flange_a, torque1.flange);
  connect(DriveSine.y, torque1.tau);
  connect(load.y, torque2.tau);
  connect(gear.support, fixed.flange);
  connect(fixed.flange, torque2.support);
  connect(fixed.flange, bearingFriction.support);
  connect(torque1.support, fixed.flange);
end LossyGearDemo2;

Modelica.Mechanics.Rotational.Examples.ElasticBearing

Information

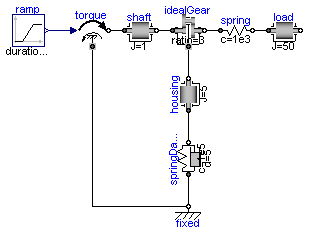
This model demonstrates the usage of the bearing flange. The gearbox is not connected rigidly to the ground, but by a spring-damper-system. This allows examination of the gearbox housing dynamics.

Simulate for about 10 seconds and plot the angular velocities of the inertias housing.w, shaft.w and load.w.

Extends from Modelica.Icons.Example (Icon for an example model).

Modelica definition

model ElasticBearing 
  "Example to show possible usage of support flange"
  extends Modelica.Icons.Example;
  Rotational.Components.Inertia shaft(        phi(fixed=true, start=0), w(
        fixed=true),
    J=1);
  Rotational.Components.Inertia load(        J=50,
    w(fixed=true));
  Rotational.Components.Spring spring(        c=1e3, phi_rel(fixed=true));
  Rotational.Components.Fixed fixed;
  Rotational.Components.SpringDamper springDamper(        c=1e5, d=5,
    phi_rel(fixed=true),
    w_rel(fixed=true));
  Rotational.Sources.Torque torque(useSupport=true);
  Modelica.Blocks.Sources.Ramp ramp(              duration=5, height=100);
  Rotational.Components.IdealGear idealGear(        ratio=3, useSupport=
        true);
  Rotational.Components.Inertia housing(
                  J=5);
equation 
  connect(torque.flange, shaft.flange_a);
  connect(spring.flange_b, load.flange_a);
  connect(springDamper.flange_a, fixed.flange);
  connect(shaft.flange_b, idealGear.flange_a);
  connect(idealGear.flange_b, spring.flange_a);
  connect(idealGear.support, housing.flange_b);
  connect(housing.flange_a, springDamper.flange_b);
  connect(ramp.y, torque.tau);
  connect(fixed.flange, torque.support);
end ElasticBearing;

Modelica.Mechanics.Rotational.Examples.Backlash

Information

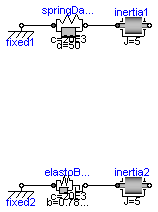
This model demonstrates the effect of a backlash on eigenfrequency, and also that the damping torque does not lead to unphysical pulling torques (since the ElastoBacklash model takes care of it).

Extends from Modelica.Icons.Example (Icon for an example model).

Modelica definition

model Backlash "Example to demonstrate backlash"
  extends Modelica.Icons.Example;
  Rotational.Components.Fixed fixed1;
  Rotational.Components.SpringDamper springDamper(c=20E3, d=50,
    phi_nominal=1);
  Rotational.Components.Inertia inertia1(J=5,
    w(fixed=true, start=0),
    phi(
      fixed=true,
      displayUnit="deg",
      start=1.570796326794897));
  Rotational.Components.Fixed fixed2;
  Rotational.Components.ElastoBacklash elastoBacklash(
    c=20E3,
    d=50,
    b(displayUnit="deg") = 0.7853981633974483,
    phi_nominal=1);
  Rotational.Components.Inertia inertia2(J=5,
    w(fixed=true, start=0),
    phi(
      fixed=true,
      start=1.570796326794897,
      displayUnit="deg"));
equation 
  connect(springDamper.flange_b, inertia1.flange_a);
  connect(elastoBacklash.flange_b, inertia2.flange_a);
  connect(fixed1.flange, springDamper.flange_a);
  connect(fixed2.flange, elastoBacklash.flange_a);
end Backlash;

Modelica.Mechanics.Rotational.Examples.RollingWheel

Information

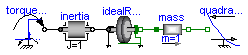
This model demonstrates the coupling between rotational and translational components:
A torque (step) accelerates both the inertia (of the wheel) and the mass (of the vehicle).
Du to a speed dependent force (like driving resistance), we find an eqilibrium at 5 m/s after approx. 5 s.

Extends from Modelica.Icons.Example (Icon for an example model).

Modelica definition

model RollingWheel "Demonstrate coupling Rotational - Translational"
  extends Modelica.Icons.Example;
  Rotational.Components.IdealRollingWheel idealRollingWheel(radius=1);
  Rotational.Components.Inertia inertia(J=1);
  Rotational.Sources.TorqueStep torqueStep(
    stepTorque=10,
    offsetTorque=0,
    startTime=0.1,
    useSupport=false);
  Translational.Components.Mass mass(L=0, m=1);
  Translational.Sources.QuadraticSpeedDependentForce
    quadraticSpeedDependentForce(
    f_nominal=-10,
    ForceDirection=false,
    v_nominal=5);
equation 

  connect(torqueStep.flange, inertia.flange_a);
  connect(inertia.flange_b, idealRollingWheel.flangeR);
  connect(idealRollingWheel.flangeT, mass.flange_a);
  connect(quadraticSpeedDependentForce.flange, mass.flange_b);
end RollingWheel;