Modelica.Mechanics.Translational.Components

Information

This package contains basic components 1D mechanical translational drive trains.

Extends from Modelica.Icons.Library2 (Icon for library where additional icon elements shall be added).

Package Content

Name	Description
Fixed	Fixed flange
Mass	Sliding mass with inertia
Rod	Rod without inertia
Spring	Linear 1D translational spring
Damper	Linear 1D translational damper
SpringDamper	Linear 1D translational spring and damper in parallel
ElastoGap	1D translational spring damper combination with gap
SupportFriction	Coulomb friction in support
Brake	Brake basend on Coulomb friction
IdealGearR2T	Gearbox transforming rotational into translational motion"
IdealRollingWheel	Simple 1-dim. model of an ideal rolling wheel without inertia
InitializeFlange	Initializes a flange with pre-defined position, speed and acceleration (usually, this is reference data from a control bus)
MassWithStopAndFriction	Sliding mass with hard stop and Stribeck friction
RelativeStates	Definition of relative state variables

Modelica.Mechanics.Translational.Components.Fixed

Information

The flange of a 1D translational mechanical system fixed at an position s0 in the housing. May be used:

• to connect a compliant element, such as a spring or a damper, between a sliding mass and the housing.
• to fix a rigid element, such as a sliding mass, at a specific position.

Parameters

Type	Name	Default	Description
Position	s0	0	fixed offset position of housing [m]

Connectors

Type	Name	Description
Flange_b	flange

Modelica definition

model Fixed "Fixed flange"
  parameter SI.Position s0=0 "fixed offset position of housing";

  Interfaces.Flange_b flange;
equation 
  flange.s = s0;
end Fixed;

Modelica.Mechanics.Translational.Components.Mass

Information

Sliding mass with inertia, without friction and two rigidly connected flanges.

The sliding mass has the length L, the position coordinate s is in the middle. Sign convention: A positive force at flange flange_a moves the sliding mass in the positive direction. A negative force at flange flange_a moves the sliding mass to the negative direction.

Extends from Translational.Interfaces.PartialRigid (Rigid connection of two translational 1D flanges ).

Parameters

Type	Name	Default	Description
Mass	m		mass of the sliding mass [kg]
Length	L	0	Length of component, from left flange to right flange (= flange_b.s - flange_a.s) [m]
Advanced
StateSelect	stateSelect	StateSelect.default	Priority to use s and v as states

Connectors

Type	Name	Description
Flange_a	flange_a	Left flange of translational component
Flange_b	flange_b	Right flange of translational component

Modelica definition

model Mass "Sliding mass with inertia"
  parameter SI.Mass m(min=0, start=1) "mass of the sliding mass";
  parameter StateSelect stateSelect=StateSelect.default 
    "Priority to use s and v as states";
  extends Translational.Interfaces.PartialRigid(L=0,s(start=0, stateSelect=stateSelect));
  SI.Velocity v(start=0, stateSelect=stateSelect) 
    "absolute velocity of component";
  SI.Acceleration a(start=0) "absolute acceleration of component";

equation 
  v = der(s);
  a = der(v);
  m*a = flange_a.f + flange_b.f;
end Mass;

Modelica.Mechanics.Translational.Components.Rod

Information

Rod without inertia and two rigidly connected flanges.

Extends from Translational.Interfaces.PartialRigid (Rigid connection of two translational 1D flanges ).

Parameters

Type	Name	Default	Description
Length	L		Length of component, from left flange to right flange (= flange_b.s - flange_a.s) [m]

Connectors

Type	Name	Description
Flange_a	flange_a	Left flange of translational component
Flange_b	flange_b	Right flange of translational component

Modelica definition

model Rod "Rod without inertia"
  extends Translational.Interfaces.PartialRigid;

equation 
  0 = flange_a.f + flange_b.f;
end Rod;

Modelica.Mechanics.Translational.Components.Spring

Information

A linear 1D translational spring. The component can be connected either between two sliding masses, or between a sliding mass and the housing (model Fixed), to describe a coupling of the sliding mass with the housing via a spring.

Extends from Translational.Interfaces.PartialCompliant (Compliant connection of two translational 1D flanges).

Parameters

Type	Name	Default	Description
TranslationalSpringConstant	c		spring constant [N/m]
Distance	s_rel0	0	unstretched spring length [m]
Initialization
Distance	s_rel.start	0	relative distance (= flange_b.s - flange_a.s) [m]

Connectors

Type	Name	Description
Flange_a	flange_a	Left flange of compliant 1-dim. translational component
Flange_b	flange_b	Right flange of compliant 1-dim. translational component

Modelica definition

model Spring "Linear 1D translational spring"
  extends Translational.Interfaces.PartialCompliant;
  parameter SI.TranslationalSpringConstant c(final min=0, start = 1) 
    "spring constant ";
  parameter SI.Distance s_rel0=0 "unstretched spring length";

equation 
  f = c*(s_rel - s_rel0);
end Spring;

Modelica.Mechanics.Translational.Components.Damper

Information

Linear, velocity dependent damper element. It can be either connected between a sliding mass and the housing (model Fixed), or between two sliding masses.

Extends from Translational.Interfaces.PartialCompliantWithRelativeStates (Base model for the compliant connection of two translational 1-dim. shaft flanges where the relative position and relative velocities are used as states).

Parameters

Type	Name	Default	Description
TranslationalDampingConstant	d		damping constant [N.s/m]
Initialization
Distance	s_rel.start	0	Relative distance (= flange_b.s - flange_a.s) [m]
Velocity	v_rel.start	0	Relative velocity (= der(s_rel)) [m/s]
Advanced
StateSelect	stateSelect	StateSelect.prefer	Priority to use phi_rel and w_rel as states
Distance	s_nominal	1e-4	Nominal value of s_rel (used for scaling) [m]

Connectors

Type	Name	Description
Flange_a	flange_a	Left flange of compliant 1-dim. translational component
Flange_b	flange_b	Right flange of compliant 1-dim. transational component

Modelica definition

model Damper "Linear 1D translational damper"
  extends Translational.Interfaces.PartialCompliantWithRelativeStates;
  parameter SI.TranslationalDampingConstant d(final min=0, start = 0) 
    "damping constant";

equation 
  f = d*v_rel;
end Damper;

Modelica.Mechanics.Translational.Components.SpringDamper

Information

A spring and damper element connected in parallel. The component can be connected either between two sliding masses to describe the elasticity and damping, or between a sliding mass and the housing (model Fixed), to describe a coupling of the sliding mass with the housing via a spring/damper.

Extends from Translational.Interfaces.PartialCompliantWithRelativeStates (Base model for the compliant connection of two translational 1-dim. shaft flanges where the relative position and relative velocities are used as states).

Parameters

Type	Name	Default	Description
TranslationalSpringConstant	c		spring constant [N/m]
TranslationalDampingConstant	d		damping constant [N.s/m]
Position	s_rel0	0	unstretched spring length [m]
Initialization
Distance	s_rel.start	0	Relative distance (= flange_b.s - flange_a.s) [m]
Velocity	v_rel.start	0	Relative velocity (= der(s_rel)) [m/s]
Advanced
StateSelect	stateSelect	StateSelect.prefer	Priority to use phi_rel and w_rel as states
Distance	s_nominal	1e-4	Nominal value of s_rel (used for scaling) [m]

Connectors

Type	Name	Description
Flange_a	flange_a	Left flange of compliant 1-dim. translational component
Flange_b	flange_b	Right flange of compliant 1-dim. transational component

Modelica definition

model SpringDamper 
  "Linear 1D translational spring and damper in parallel"
  extends Translational.Interfaces.PartialCompliantWithRelativeStates;
  parameter SI.TranslationalSpringConstant c(final min=0, start = 1) 
    "spring constant";
  parameter SI.TranslationalDampingConstant d(final min=0, start = 1) 
    "damping constant";
  parameter SI.Position s_rel0=0 "unstretched spring length";

equation 
  f = c*(s_rel - s_rel0) + d*v_rel;
end SpringDamper;

Modelica.Mechanics.Translational.Components.ElastoGap

Information

A linear spring damper combination that can lift off. The component can be connected between a sliding mass and the housing (model Fixed), to describe the contact of a sliding mass with the housing.

As long as s_rel > s_rel0, no force is exerted (s_rel = flange_b.s - flange_a.s). If s_rel ≤ s_rel0, the contact force is basically computed with a linear spring/damper characteristic. With parameter n≥1 (exponent of spring force), a nonlinear spring force can be modeled:

   desiredContactForce = c*|s_rel - s_rel0|^n + d*der(s_rel)

Note, Hertzian contact is described by:

• Contact between two metallic spheres: n=1.5
• Contact between two metallic plates: n=1

The above force law leads to the following difficulties:

1. If the damper force becomes larger as the spring force and with opposite sign, the contact force would be "pulling/sticking" which is unphysical, since during contact only pushing forces can occur.
2. When contact occurs with a non-zero relative speed (which is the usual situation), the damping force has a non-zero value and therefore the contact force changes discontinuously at s_rel = s_rel0. Again, this is not physical because the force can only change continuously. (Note, this component is not an idealized model where a steep characteristic is approximated by a discontinuity, but it shall model the steep characteristic.)

In the literature there are several proposals to fix problem (2). Especially, often the following model is used (see, e.g., Lankarani, Nikravesh: Continuous Contact Force Models for Impact Analysis in Multibody Systems, Nonlinear Dynamics 5, pp. 193-207, 1994, pdf-download):

   f = c*s_rel^n + (d*s_rel^n)*der(s_rel)

However, this and other models proposed in literature violate issue (1), i.e., unphysical pulling forces can occur (if d*der(s_rel) becomes large enough). Note, if the force law is of the form "f = f_c + f_d", then a necessary condition is that |f_d| ≤ |f_c|, otherwise (1) and (2) are violated. For this reason, the most simplest approach is used in the ElastoGap model to fix both problems by using this necessary condition in the force law directly. If s_rel0 = 0, the equations are:

    if s_rel ≥ 0 then
       f = 0;    // contact force
    else
       f_c  = -c*|s_rel|^n;          // contact spring force (Hertzian contact force)
       f_d2 = d*der(s_rel);         // linear contact damper force
       f_d  = if f_d2 <  f_c then  f_c else
              if f_d2 > -f_c then -f_c else f_d2;  // bounded damper force
       f    = f_c + f_d;            // contact force
    end if;

Note, since |f_d| ≤ |f_c|, pulling forces cannot occur and the contact force is always continuous, especially around the start of the penetration at s_rel = s_rel0.

In the next figure, a typical simulation with the ElastoGap model is shown (Examples.ElastoGap) where the different effects are visualized:

1. Curve 1 (elastoGap1.f) is the unmodified contact force, i.e., the linear spring/damper characteristic. A pulling/sticking force is present at the end of the contact.
2. Curve 2 (elastoGap2.f) is the contact force, where the force is explicitly set to zero when pulling/sticking occurs. The contact force is discontinuous at being of the contact.
3. Curve 3 (elastoGap3.f) is the ElastoGap model of this library. No discontinuity and no pulling/sticking occurs.

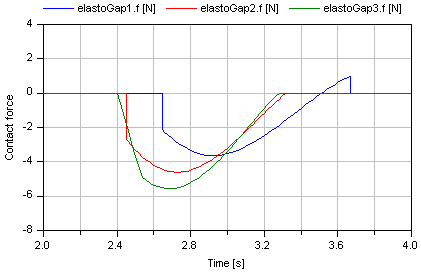
Extends from Modelica.Mechanics.Translational.Interfaces.PartialCompliantWithRelativeStates (Base model for the compliant connection of two translational 1-dim. shaft flanges where the relative position and relative velocities are used as states).

Parameters

Type	Name	Default	Description
Real	c		Spring constant [N/m]
Real	d		Damping constant [N/ (m/s)]
Position	s_rel0	0	Unstretched spring length [m]
Real	n	1	Exponent of spring force ( f_c = -c*|s_rel-s_rel0|^n )
Initialization
Distance	s_rel.start	0	Relative distance (= flange_b.s - flange_a.s) [m]
Velocity	v_rel.start	0	Relative velocity (= der(s_rel)) [m/s]
Advanced
StateSelect	stateSelect	StateSelect.prefer	Priority to use phi_rel and w_rel as states
Distance	s_nominal	1e-4	Nominal value of s_rel (used for scaling) [m]

Connectors

Type	Name	Description
Flange_a	flange_a	Left flange of compliant 1-dim. translational component
Flange_b	flange_b	Right flange of compliant 1-dim. transational component

Modelica definition

model ElastoGap "1D translational spring damper combination with gap"
  extends Modelica.Mechanics.Translational.Interfaces.PartialCompliantWithRelativeStates;
  parameter Real c(final unit="N/m", final min=0, start=1) "Spring constant";
  parameter Real d(final unit="N/ (m/s)", final min=0, start=1) 
    "Damping constant";
  parameter Modelica.SIunits.Position s_rel0=0 "Unstretched spring length";
  parameter Real n(final min=1) = 1 
    "Exponent of spring force ( f_c = -c*|s_rel-s_rel0|^n )";

/*
Please note that initialization might fail due to the nonlinear spring characteristic
(spring force is zero for s_rel > s_rel0)
if a positive force is acting on the element and no other force balances this force
(e.g. when setting both initial velocity and acceleration to 0)
*/
  Boolean contact "=true, if contact, otherwise no contact";
protected 
  Modelica.SIunits.Force f_c "Spring force";
  Modelica.SIunits.Force f_d2 "Linear damping force";
  Modelica.SIunits.Force f_d 
    "Linear damping force which is limited by spring force (|f_d| <= |f_c|)";
equation 
  // Modify contact force, so that it is only "pushing" and not
  // "pulling/sticking" and that it is continous
  contact = s_rel < s_rel0;
  f_c  = smooth(1, noEvent( if contact then -c*abs(s_rel - s_rel0)^n else 0));
  f_d2 = if contact then d*v_rel else 0;
  f_d  = smooth(0, noEvent( if contact then (if f_d2 <  f_c then  f_c else 
                                             if f_d2 > -f_c then -f_c else f_d2) else 0));
  f = f_c + f_d;
end ElastoGap;

Modelica.Mechanics.Translational.Components.SupportFriction

Information

This element describes Coulomb friction in support, i.e., a frictional force acting between a flange and the housing. The positive sliding friction force "f" has to be defined by table "f_pos" as function of the absolute velocity "v". E.g.

       v |   f
      ---+-----
       0 |   0
       1 |   2
       2 |   5
       3 |   8

gives the following table:

   f_pos = [0, 0; 1, 2; 2, 5; 3, 8];

Currently, only linear interpolation in the table is supported. Outside of the table, extrapolation through the last two table entries is used. It is assumed that the negative sliding friction force has the same characteristic with negative values. Friction is modelled in the following way:

When the absolute velocity "v" is not zero, the friction force is a function of v and of a constant normal force. This dependency is defined via table f_pos and can be determined by measurements, e.g. by driving the gear with constant velocity and measuring the needed driving force (= friction force).

When the absolute velocity becomes zero, the elements connected by the friction element become stuck, i.e., the absolute position remains constant. In this phase the friction force is calculated from a force balance due to the requirement, that the absolute acceleration shall be zero. The elements begin to slide when the friction force exceeds a threshold value, called the maximum static friction force, computed via:

   maximum_static_friction = peak * sliding_friction(v=0)  (peak >= 1)

This procedure is implemented in a "clean" way by state events and leads to continuous/discrete systems of equations if friction elements are dynamically coupled which have to be solved by appropriate numerical methods. The method is described in:

Otter M., Elmqvist H., and Mattsson S.E. (1999):

Hybrid Modeling in Modelica based on the Synchronous Data Flow Principle. CACSD'99, Aug. 22.-26, Hawaii.

More precise friction models take into account the elasticity of the material when the two elements are "stuck", as well as other effects, like hysteresis. This has the advantage that the friction element can be completely described by a differential equation without events. The drawback is that the system becomes stiff (about 10-20 times slower simulation) and that more material constants have to be supplied which requires more sophisticated identification. For more details, see the following references, especially (Armstrong and Canudas de Witt 1996):

Armstrong B. (1991):

Control of Machines with Friction. Kluwer Academic Press, Boston MA.

Armstrong B., and Canudas de Wit C. (1996):

Friction Modeling and Compensation. The Control Handbook, edited by W.S.Levine, CRC Press, pp. 1369-1382.

Canudas de Wit C., Olsson H., Astroem K.J., and Lischinsky P. (1995):

A new model for control of systems with friction. IEEE Transactions on Automatic Control, Vol. 40, No. 3, pp. 419-425.

Extends from Modelica.Mechanics.Translational.Interfaces.PartialElementaryTwoFlangesAndSupport2 (Partial model for a component with one translational 1-dim. shaft flange and a support used for textual modeling, i.e., for elementary models), Translational.Interfaces.PartialFriction (Base model of Coulomb friction elements).

Parameters

Type	Name	Default	Description
Boolean	useSupport	false	= true, if support flange enabled, otherwise implicitly grounded
Real	f_pos[:, 2]	[0, 1]	[v, f] Positive sliding friction characteristic (v>=0)
Real	peak	1	peak*f_pos[1,2] = Maximum friction force for v==0
Initialization
Boolean	startForward.start	false	true, if v_rel=0 and start of forward sliding
Boolean	startBackward.start	false	true, if v_rel=0 and start of backward sliding
Boolean	locked.start	false	true, if v_rel=0 and not sliding
Advanced
Velocity	v_small	1e-3	Relative velocity near to zero (see model info text) [m/s]

Connectors

Type	Name	Description
Flange_a	flange_a	Flange of left shaft
Flange_b	flange_b	Flange of right shaft
Support	support	Support/housing of component

Modelica definition

model SupportFriction "Coulomb friction in support"

  extends Modelica.Mechanics.Translational.Interfaces.PartialElementaryTwoFlangesAndSupport2;
  parameter Real f_pos[:, 2]=[0, 1] 
    "[v, f] Positive sliding friction characteristic (v>=0)";
  parameter Real peak(final min=1) = 1 
    "peak*f_pos[1,2] = Maximum friction force for v==0";
  extends Translational.Interfaces.PartialFriction;

  SI.Position s;
  SI.Force f "Friction force";
  SI.Velocity v "Absolute velocity of flange_a and flange_b";
  SI.Acceleration a "Absolute acceleration of flange_a and flange_b";
equation 
  // Constant auxiliary variables
  f0 = Modelica.Math.tempInterpol1(0, f_pos, 2);
  f0_max = peak*f0;
  free = false;

  s = s_a - s_support;
  s_a = s_b;

// velocity and acceleration of flanges
  v = der(s);
  a = der(v);
  v_relfric = v;
  a_relfric = a;

// Friction force
  flange_a.f + flange_b.f - f = 0;

// Friction force
  f = if locked then sa*unitForce else 
     (if startForward then          Modelica.Math.tempInterpol1( v, f_pos, 2) else 
      if startBackward then        -Modelica.Math.tempInterpol1(-v, f_pos, 2) else 
      if pre(mode) == Forward then  Modelica.Math.tempInterpol1( v, f_pos, 2) else 
                                   -Modelica.Math.tempInterpol1(-v, f_pos, 2));
end SupportFriction;

Modelica.Mechanics.Translational.Components.Brake

Information

This component models a brake, i.e., a component where a frictional force is acting between the housing and a flange and a controlled normal force presses the flange to the housing in order to increase friction. The normal force fn has to be provided as input signal f_normalized in a normalized form (0 ≤ f_normalized ≤ 1), fn = fn_max*f_normalized, where fn_max has to be provided as parameter. Friction in the brake is modelled in the following way:

When the absolute velocity "v" is not zero, the friction force is a function of the velocity dependent friction coefficient mue(v) , of the normal force "fn", and of a geometry constant "cgeo" which takes into account the geometry of the device and the assumptions on the friction distributions:

        frictional_force = cgeo * mue(v) * fn

Typical values of coefficients of friction:

      dry operation   :  mue = 0.2 .. 0.4
      operating in oil:  mue = 0.05 .. 0.1

The positive part of the friction characteristic mue(v), v >= 0, is defined via table mue_pos (first column = v, second column = mue). Currently, only linear interpolation in the table is supported.

When the absolute velocity becomes zero, the elements connected by the friction element become stuck, i.e., the absolute position remains constant. In this phase the friction force is calculated from a force balance due to the requirement, that the absolute acceleration shall be zero. The elements begin to slide when the friction force exceeds a threshold value, called the maximum static friction force, computed via:

       frictional_force = peak * cgeo * mue(w=0) * fn   (peak >= 1)

This procedure is implemented in a "clean" way by state events and leads to continuous/discrete systems of equations if friction elements are dynamically coupled. The method is described in:

Otter M., Elmqvist H., and Mattsson S.E. (1999):

Hybrid Modeling in Modelica based on the Synchronous Data Flow Principle. CACSD'99, Aug. 22.-26, Hawaii.

More precise friction models take into account the elasticity of the material when the two elements are "stuck", as well as other effects, like hysteresis. This has the advantage that the friction element can be completely described by a differential equation without events. The drawback is that the system becomes stiff (about 10-20 times slower simulation) and that more material constants have to be supplied which requires more sophisticated identification. For more details, see the following references, especially (Armstrong and Canudas de Witt 1996):

Armstrong B. (1991):

Control of Machines with Friction. Kluwer Academic Press, Boston MA.

Armstrong B., and Canudas de Wit C. (1996):

Friction Modeling and Compensation. The Control Handbook, edited by W.S.Levine, CRC Press, pp. 1369-1382.

Canudas de Wit C., Olsson H., Astroem K.J., and Lischinsky P. (1995):

A new model for control of systems with friction. IEEE Transactions on Automatic Control, Vol. 40, No. 3, pp. 419-425.

Extends from Modelica.Mechanics.Translational.Interfaces.PartialElementaryTwoFlangesAndSupport2 (Partial model for a component with one translational 1-dim. shaft flange and a support used for textual modeling, i.e., for elementary models), Translational.Interfaces.PartialFriction (Base model of Coulomb friction elements).

Parameters

Type	Name	Default	Description
Boolean	useSupport	false	= true, if support flange enabled, otherwise implicitly grounded
Real	mue_pos[:, 2]	[0, 0.5]	[v, f] Positive sliding friction characteristic (v>=0)
Real	peak	1	peak*mue_pos[1,2] = Maximum friction force for v==0
Real	cgeo	1	Geometry constant containing friction distribution assumption
Force	fn_max		Maximum normal force [N]
Initialization
Boolean	startForward.start	false	true, if v_rel=0 and start of forward sliding
Boolean	startBackward.start	false	true, if v_rel=0 and start of backward sliding
Boolean	locked.start	false	true, if v_rel=0 and not sliding
Advanced
Velocity	v_small	1e-3	Relative velocity near to zero (see model info text) [m/s]

Connectors

Type	Name	Description
Flange_a	flange_a	Flange of left shaft
Flange_b	flange_b	Flange of right shaft
Support	support	Support/housing of component
input RealInput	f_normalized	Normalized force signal 0..1 (normal force = fn_max*f_normalized; brake is active if > 0)

Modelica definition

model Brake "Brake basend on Coulomb friction"

  extends Modelica.Mechanics.Translational.Interfaces.PartialElementaryTwoFlangesAndSupport2;
  parameter Real mue_pos[:, 2]=[0, 0.5] 
    "[v, f] Positive sliding friction characteristic (v>=0)";
  parameter Real peak(final min=1) = 1 
    "peak*mue_pos[1,2] = Maximum friction force for v==0";
  parameter Real cgeo(final min=0) = 1 
    "Geometry constant containing friction distribution assumption";
  parameter SI.Force fn_max(final min=0, start=1) "Maximum normal force";
  extends Translational.Interfaces.PartialFriction;

  SI.Position s;
  SI.Force f "Brake friction force";
  SI.Velocity v "Absolute velocity of flange_a and flange_b";
  SI.Acceleration a "Absolute acceleration of flange_a and flange_b";

  Real mue0 "Friction coefficient for v=0 and forward sliding";
  SI.Force fn "Normal force (=fn_max*f_normalized)";

  // Constant auxiliary variable
  Modelica.Blocks.Interfaces.RealInput f_normalized 
    "Normalized force signal 0..1 (normal force = fn_max*f_normalized; brake is active if > 0)";
    
equation 
  mue0 = Modelica.Math.tempInterpol1(0, mue_pos, 2);

  s = s_a;
  s = s_b;

// velocity and acceleration of flanges flange_a and flange_b
  v = der(s);
  a = der(v);
  v_relfric = v;
  a_relfric = a;

// Friction force, normal force and friction force for v_rel=0
  flange_a.f + flange_b.f - f = 0;
  fn = fn_max*f_normalized;
  f0 = mue0*cgeo*fn;
  f0_max = peak*f0;
  free = fn <= 0;

  // friction force
  f = if locked then sa*unitForce else 
      if free then   0 else 
      cgeo*fn*(if startForward then          Modelica.Math.tempInterpol1( v, mue_pos, 2) else 
               if startBackward then        -Modelica.Math.tempInterpol1(-v, mue_pos, 2) else 
               if pre(mode) == Forward then  Modelica.Math.tempInterpol1( v, mue_pos, 2) else 
                                            -Modelica.Math.tempInterpol1(-v, mue_pos, 2));
end Brake;

Modelica.Mechanics.Translational.Components.IdealGearR2T

Information

Parameters

Type	Name	Default	Description
Boolean	useSupportR	false	= true, if rotational support flange enabled, otherwise implicitly grounded
Boolean	useSupportT	false	= true, if translational support flange enabled, otherwise implicitly grounded
Real	ratio		Transmission ratio (flange_a.phi/flange_b.s) [rad/m]

Connectors

Type	Name	Description
Flange_a	flangeR	Flange of rotational shaft
Flange_b	flangeT	Flange of translational rod
Support	supportR	Rotational support/housing of component
Support	supportT	Translational support/housing of component

Modelica definition

model IdealGearR2T 
  "Gearbox transforming rotational into translational motion\""
  extends Modelica.Mechanics.Rotational.Components.IdealGearR2T;
equation 

end IdealGearR2T;

Modelica.Mechanics.Translational.Components.IdealRollingWheel

Information

Parameters

Type	Name	Default	Description
Boolean	useSupportR	false	= true, if rotational support flange enabled, otherwise implicitly grounded
Boolean	useSupportT	false	= true, if translational support flange enabled, otherwise implicitly grounded
Distance	radius		Wheel radius [m]

Connectors

Type	Name	Description
Flange_a	flangeR	Flange of rotational shaft
Flange_b	flangeT	Flange of translational rod
Support	supportR	Rotational support/housing of component
Support	supportT	Translational support/housing of component

Modelica definition

model IdealRollingWheel 
  "Simple 1-dim. model of an ideal rolling wheel without inertia"
  extends Modelica.Mechanics.Rotational.Components.IdealRollingWheel;
equation 

end IdealRollingWheel;

Modelica.Mechanics.Translational.Components.InitializeFlange

Information

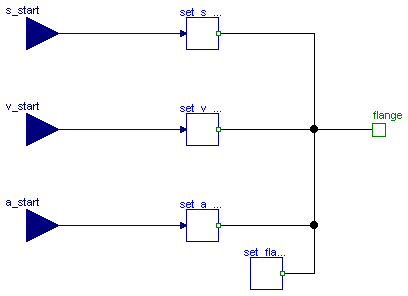
This component is used to optionally initialize the position, speed, and/or acceleration of the flange to which this component is connected. Via parameters use_s_start, use_v_start, use_a_start the corresponding input signals s_start, v_start, a_start are conditionally activated. If an input is activated, the corresponding flange property is initialized with the input value at start time.

For example, if "use_s_start = true", then flange.s is initialized with the value of the input signal "s_start" at the start time.

Additionally, it is optionally possible to define the "StateSelect" attribute of the flange position and the flange speed via paramater "stateSelection".

This component is especially useful when the initial values of a flange shall be set according to reference signals of a controller that are provided via a signal bus.

Extends from Modelica.Blocks.Interfaces.BlockIcon (Basic graphical layout of input/output block).

Parameters

Type	Name	Default	Description
Boolean	use_s_start	true	= true, if initial position is defined by input s_start, otherwise not initialized
Boolean	use_v_start	true	= true, if initial speed is defined by input v_start, otherwise not initialized
Boolean	use_a_start	true	= true, if initial acceleration is defined by input a_start, otherwise not initialized
StateSelect	stateSelect	StateSelect.default	Priority to use flange angle and speed as states

Connectors

Type	Name	Description
input RealInput	s_start	Initial position of flange
input RealInput	v_start	Initial speed of flange
input RealInput	a_start	Initial angular acceleration of flange
Flange_b	flange	Flange that is initialized

Modelica definition

model InitializeFlange 
  "Initializes a flange with pre-defined position, speed and acceleration (usually, this is reference data from a control bus)"
  extends Modelica.Blocks.Interfaces.BlockIcon;
  parameter Boolean use_s_start = true 
    "= true, if initial position is defined by input s_start, otherwise not initialized";
  parameter Boolean use_v_start = true 
    "= true, if initial speed is defined by input v_start, otherwise not initialized";
  parameter Boolean use_a_start = true 
    "= true, if initial acceleration is defined by input a_start, otherwise not initialized";

  parameter StateSelect stateSelect=StateSelect.default 
    "Priority to use flange angle and speed as states";

  Modelica.Blocks.Interfaces.RealInput s_start if use_s_start 
    "Initial position of flange";
  Modelica.Blocks.Interfaces.RealInput v_start if use_v_start 
    "Initial speed of flange";
  Modelica.Blocks.Interfaces.RealInput a_start if use_a_start 
    "Initial angular acceleration of flange";
  Interfaces.Flange_b flange "Flange that is initialized";

  Modelica.SIunits.Position s_flange(stateSelect=stateSelect)=flange.s 
    "Flange position";
  Modelica.SIunits.Velocity v_flange(stateSelect=stateSelect)= der(s_flange) 
    "= der(s_flange)";

protected 
  encapsulated model Set_s_start "Set s_start"
    import Modelica;
    extends Modelica.Blocks.Interfaces.BlockIcon;
    Modelica.Blocks.Interfaces.RealInput s_start "Start position";

    Modelica.Mechanics.Translational.Interfaces.Flange_b flange;
  initial equation 
    flange.s = s_start;
  equation 
    flange.f = 0;
  end Set_s_start;

  encapsulated model Set_v_start "Set v_start"
    import Modelica;
    extends Modelica.Blocks.Interfaces.BlockIcon;
    Modelica.Blocks.Interfaces.RealInput v_start "Start velocity";

    Modelica.Mechanics.Translational.Interfaces.Flange_b flange;
  initial equation 
    der(flange.s) = v_start;
  equation 
    flange.f = 0;
  end Set_v_start;

  encapsulated model Set_a_start "Set a_start"
    import Modelica;
    extends Modelica.Blocks.Interfaces.BlockIcon;
    Modelica.Blocks.Interfaces.RealInput a_start "Start acceleration";

    Modelica.Mechanics.Translational.Interfaces.Flange_b flange(s(stateSelect=StateSelect.avoid));
    Modelica.SIunits.Velocity v = der(flange.s);
  initial equation 
    der(v) = a_start;
  equation 
    flange.f = 0;
  end Set_a_start;

  encapsulated model Set_flange_f "Set flange_f to zero"
    import Modelica;
    extends Modelica.Blocks.Interfaces.BlockIcon;
    Modelica.Mechanics.Translational.Interfaces.Flange_b flange;
  equation 
    flange.f = 0;
  end Set_flange_f;
protected 
  Set_s_start set_s_start if use_s_start;
  Set_v_start set_v_start if use_v_start;
  Set_a_start set_a_start if use_a_start;
  Set_flange_f set_flange_f;
equation 
  connect(set_s_start.flange, flange);
  connect(set_v_start.flange, flange);
  connect(set_a_start.flange, flange);
  connect(set_flange_f.flange, flange);
  connect(s_start, set_s_start.s_start);
  connect(v_start, set_v_start.v_start);
  connect(a_start, set_a_start.a_start);
end InitializeFlange;

Modelica.Mechanics.Translational.Components.MassWithStopAndFriction

Information

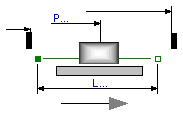
This element describes the Stribeck friction characteristics of a sliding mass, i. e. the frictional force acting between the sliding mass and the support. Included is a hard stop for the position.
The surface is fixed and there is friction between sliding mass and surface. The frictional force f is given for positive velocity v by:

f = F_Coulomb + F_prop * v + F_Stribeck * exp (-fexp * v)

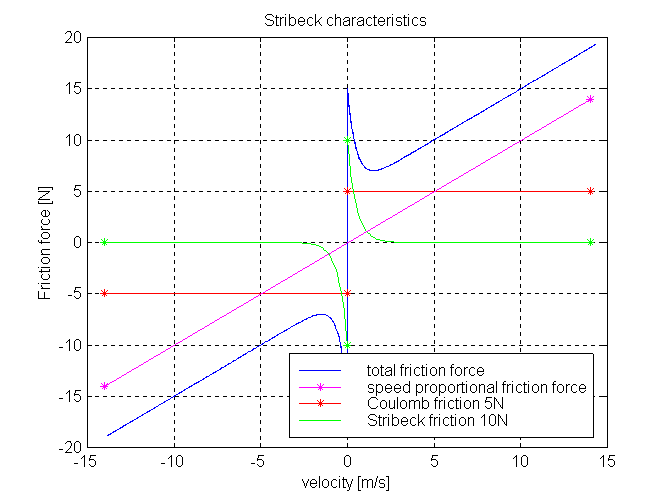
There are hard stops at smax and smin, i. e. if

flange_a.s >= smin
and
flange_b.s <= xmax

When the absolute velocity becomes zero, the sliding mass becomes stuck, i.e., the absolute position remains constant. In this phase the friction force is calculated from a force balance due to the requirement that the absolute acceleration shall be zero. The elements begin to slide when the friction force exceeds a threshold value, called the maximum static friction force, computed via:

maximum_static_friction = F_Coulomb + F_Stribeck

For more details of the used friction model see the following reference:

Beater P. (1999):

Entwurf hydraulischer Maschinen. Springer Verlag Berlin Heidelberg New York.

The friction model is implemented in a "clean" way by state events and leads to continuous/discrete systems of equations which have to be solved by appropriate numerical methods. The method is described in:

Otter M., Elmqvist H., and Mattsson S.E. (1999):

Hybrid Modeling in Modelica based on the Synchronous Data Flow Principle. CACSD'99, Aug. 22.-26, Hawaii.

More precise friction models take into account the elasticity of the material when the two elements are "stuck", as well as other effects, like hysteresis. This has the advantage that the friction element can be completely described by a differential equation without events. The drawback is that the system becomes stiff (about 10-20 times slower simulation) and that more material constants have to be supplied which requires more sophisticated identification. For more details, see the following references, especially (Armstrong and Canudas de Witt 1996):

Armstrong B. (1991):

Control of Machines with Friction. Kluwer Academic Press, Boston MA.

Armstrong B., and Canudas de Wit C. (1996):

Friction Modeling and Compensation. The Control Handbook, edited by W.S.Levine, CRC Press, pp. 1369-1382.

Canudas de Wit C., Olsson H., Astroem K.J., and Lischinsky P. (1995):

A new model for control of systems with friction. IEEE Transactions on Automatic Control, Vol. 40, No. 3, pp. 419-425.

Extends from PartialFrictionWithStop (Base model of Coulomb friction elements with stop).

Parameters

Type	Name	Default	Description
Position	smax		Right stop for (right end of) sliding mass [m]
Position	smin		Left stop for (left end of) sliding mass [m]
Length	L		Length of component, from left flange to right flange (= flange_b.s - flange_a.s) [m]
Mass	m		mass [kg]
Real	F_prop		Velocity dependent friction [N.s/m]
Force	F_Coulomb		Constant friction: Coulomb force [N]
Force	F_Stribeck		Stribeck effect [N]
Real	fexp		Exponential decay [s/m]
Initialization
Boolean	startForward.start	false	= true, if v_rel=0 and start of forward sliding or v_rel > v_small
Boolean	startBackward.start	false	= true, if v_rel=0 and start of backward sliding or v_rel < -v_small
Boolean	locked.start	false	true, if v_rel=0 and not sliding
Position	s.start	0	Absolute position of center of component (s = flange_a.s + L/2 = flange_b.s - L/2) [m]
Advanced
Velocity	v_small	1e-3	Relative velocity near to zero (see model info text) [m/s]

Connectors

Type	Name	Description
Flange_a	flange_a	Left flange of translational component
Flange_b	flange_b	Right flange of translational component

Modelica definition

model MassWithStopAndFriction 
  "Sliding mass with hard stop and Stribeck friction"
  extends PartialFrictionWithStop;
  SI.Velocity v(start=0, stateSelect = StateSelect.always) 
    "Absolute velocity of flange_a and flange_b";
  SI.Acceleration a(start=0) "Absolute acceleration of flange_a and flange_b";
  parameter Modelica.SIunits.Mass m(start=1) "mass";
  parameter Real F_prop(final unit="N.s/m", final min=0, start = 1) 
    "Velocity dependent friction";
  parameter Modelica.SIunits.Force F_Coulomb(start=5) 
    "Constant friction: Coulomb force";
  parameter Modelica.SIunits.Force F_Stribeck(start=10) "Stribeck effect";
  parameter Real fexp(final unit="s/m", final min=0, start = 2) 
    "Exponential decay";
  Integer stopped = if s <= smin + L/2 then -1 else if s >= smax - L/2 then +1 else 0;
encapsulated partial model PartialFrictionWithStop 
    "Base model of Coulomb friction elements with stop"

    import SI = Modelica.SIunits;
    import Modelica.Mechanics.Translational.Interfaces.PartialRigid;
  parameter SI.Position smax(start= 25) 
      "Right stop for (right end of) sliding mass";
  parameter SI.Position smin(start=-25) 
      "Left stop for (left end of) sliding mass";
  parameter SI.Velocity v_small=1e-3 
      "Relative velocity near to zero (see model info text)";
// Equations to define the following variables have to be defined in subclasses
  SI.Velocity v_relfric "Relative velocity between frictional surfaces";
  SI.Acceleration a_relfric "Relative acceleration between frictional surfaces";
  SI.Force f 
      "Friction force (positive, if directed in opposite direction of v_rel)";
  SI.Force f0 "Friction force for v=0 and forward sliding";
  SI.Force f0_max "Maximum friction force for v=0 and locked";
  Boolean free "true, if frictional element is not active";
// Equations to define the following variables are given in this class
  Real sa(unit="1") 
      "Path parameter of friction characteristic f = f(a_relfric)";
  Boolean startForward(start=false, fixed=true) 
      "= true, if v_rel=0 and start of forward sliding or v_rel > v_small";
  Boolean startBackward(start=false, fixed=true) 
      "= true, if v_rel=0 and start of backward sliding or v_rel < -v_small";
  Boolean locked(start=false) "true, if v_rel=0 and not sliding";
  extends PartialRigid(s(start=0, stateSelect = StateSelect.always));
  constant Integer Unknown=3 "Value of mode is not known";
  constant Integer Free=2 "Element is not active";
  constant Integer Forward=1 "v_rel > 0 (forward sliding)";
  constant Integer Stuck=0 
      "v_rel = 0 (forward sliding, locked or backward sliding)";
  constant Integer Backward=-1 "v_rel < 0 (backward sliding)";
  Integer mode(
    final min=Backward,
    final max=Unknown,
    start=Unknown, fixed=true);
  protected 
  constant SI.Acceleration unitAcceleration = 1;
  constant SI.Force unitForce = 1;
equation 
/* Friction characteristic
   (locked is introduced to help the Modelica translator determining
   the different structural configurations,
   if for each configuration special code shall be generated)
*/
  startForward = pre(mode) == Stuck and (sa > f0_max/unitForce and s < (smax - L/2) or 
        pre(startForward) and sa > f0/unitForce and s < (smax - L/2)) or pre(mode)
     == Backward and v_relfric > v_small or initial() and (v_relfric > 0);
  startBackward = pre(mode) == Stuck and (sa < -f0_max/unitForce and s > (smin + L/2) or 
        pre(startBackward) and sa < -f0/unitForce and s > (smin + L/2)) or pre(mode)
     == Forward and v_relfric < -v_small or initial() and (v_relfric < 0);
  locked = not free and 
    not (pre(mode) == Forward or startForward or pre(mode) == Backward or startBackward);

  a_relfric/unitAcceleration = if locked then               0 else 
                               if free then                 sa else 
                               if startForward then         sa - f0_max/unitForce else 
                               if startBackward then        sa + f0_max/unitForce else 
                               if pre(mode) == Forward then sa - f0_max/unitForce else 
                                                            sa + f0_max/unitForce;

/* Friction torque has to be defined in a subclass. Example for a clutch:
   f = if locked then sa else
       if free then   0 else
       cgeo*fn*(if startForward then          Math.tempInterpol1( v_relfric, mue_pos, 2) else
                if startBackward then        -Math.tempInterpol1(-v_relfric, mue_pos, 2) else
                if pre(mode) == Forward then  Math.tempInterpol1( v_relfric, mue_pos, 2) else
                                             -Math.tempInterpol1(-v_relfric, mue_pos, 2));
*/
// finite state machine to determine configuration
  mode = if free then Free else 
    (if (pre(mode) == Forward  or pre(mode) == Free or startForward)  and v_relfric > 0 and s < (smax - L/2) then 
       Forward else 
     if (pre(mode) == Backward or pre(mode) == Free or startBackward) and v_relfric < 0 and s > (smin + L/2) then 
       Backward else 
       Stuck);
end PartialFrictionWithStop;
equation 
  // Constant auxiliary variables
  f0 = (F_Coulomb + F_Stribeck);
  f0_max = f0*1.001;
  free = f0 <= 0 and F_prop <= 0 and s > smin + L/2 and s < smax - L/2;
  // Velocity and acceleration of flanges
  v = der(s);
  a = der(v);
  v_relfric = v;
  a_relfric = a;
// Equilibrium of forces
  0 = flange_a.f + flange_b.f - f - m*der(v);
// Friction force
  f = if locked then sa*unitForce else 
      if free then   0 else 
                    (if startForward then         F_prop*v + F_Coulomb + F_Stribeck else 
                     if startBackward then        F_prop*v - F_Coulomb - F_Stribeck else 
                     if pre(mode) == Forward then F_prop*v + F_Coulomb + F_Stribeck*exp(-fexp*abs(v)) else 
                                                  F_prop*v - F_Coulomb - F_Stribeck*exp(-fexp*abs(v)));
// Define events for hard stops and reinitiliaze the state variables velocity v and position s
algorithm 
  when (initial()) then
    assert(s > smin + L/2 or s >= smin + L/2 and v >= 0,
      "Error in initialization of hard stop. (s - L/2) must be >= smin ");
    assert(s < smax - L/2 or s <= smax - L/2 and v <= 0,
      "Error in initialization of hard stop. (s + L/2) must be <= smax ");
  end when;
  when stopped <> 0 then
    reinit(s, if stopped < 0 then smin + L/2 else smax - L/2);
    if (not initial() or stopped*v>0) then
      reinit(v, 0);
    end if;
  end when;
/*
  when not (s < smax - L/2) then
    reinit(s, smax - L/2);
    if (not initial() or v>0) then
      reinit(v, 0);
    end if;
  end when;

  when not (s > smin + L/2) then
    reinit(s, smin + L/2);
    if (not initial() or v<0) then
      reinit(v, 0);
    end if;
  end when;
*/
end MassWithStopAndFriction;

---

Modelica.Mechanics.Translational.Components.RelativeStates

Definition of relative state variables

Information

Usually, the absolute position and the absolute velocity of Modelica.Mechanics.Translational.Inertia models are used as state variables. In some circumstances, relative quantities are better suited, e.g., because it may be easier to supply initial values. In such cases, model RelativeStates allows the definition of state variables in the following way:

• Connect an instance of this model between two flange connectors.
• The relative position and the relative velocity between the two connectors are used as state variables.

An example is given in the next figure

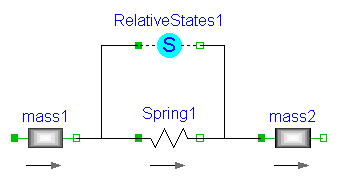
Here, the relative position and the relative velocity between the two masses are used as state variables. Additionally, the simulator selects either the absolute position and absolute velocity of model mass1 or of model mass2 as state variables.

Extends from Translational.Interfaces.PartialTwoFlanges (Component with two translational 1D flanges ).

Parameters

Type	Name	Default	Description
StateSelect	stateSelect	StateSelect.prefer	Priority to use the relative angle and relative speed as states

Connectors

Type	Name	Description
Flange_a	flange_a	(left) driving flange (flange axis directed in to cut plane, e. g. from left to right)
Flange_b	flange_b	(right) driven flange (flange axis directed out of cut plane)

Modelica definition

model RelativeStates "Definition of relative state variables"
  extends Translational.Interfaces.PartialTwoFlanges;
  parameter StateSelect stateSelect=StateSelect.prefer 
    "Priority to use the relative angle and relative speed as states";
  SI.Position s_rel(start=0, stateSelect=StateSelect.prefer) 
    "relative position used as state variable";
  SI.Velocity v_rel(start=0, stateSelect=StateSelect.prefer) 
    "relative velocity used as state variable";
  SI.Acceleration a_rel(start=0) "relative angular acceleration";

equation 
  s_rel = flange_b.s - flange_a.s;
  v_rel = der(s_rel);
  a_rel = der(v_rel);
  flange_a.f = 0;
  flange_b.f = 0;
end RelativeStates;

---

Modelica.Mechanics.Translational.Components.InitializeFlange.Set_s_start

Set s_start

Information

Extends from Modelica.Blocks.Interfaces.BlockIcon (Basic graphical layout of input/output block).

Connectors

Type	Name	Description
input RealInput	s_start	Start position
Flange_b	flange

Modelica definition

encapsulated model Set_s_start "Set s_start"
  import Modelica;
  extends Modelica.Blocks.Interfaces.BlockIcon;
  Modelica.Blocks.Interfaces.RealInput s_start "Start position";

  Modelica.Mechanics.Translational.Interfaces.Flange_b flange;
initial equation 
  flange.s = s_start;
equation 
  flange.f = 0;
end Set_s_start;

---

Modelica.Mechanics.Translational.Components.InitializeFlange.Set_v_start

Set v_start

Information

Extends from Modelica.Blocks.Interfaces.BlockIcon (Basic graphical layout of input/output block).

Connectors

Type	Name	Description
input RealInput	v_start	Start velocity
Flange_b	flange

Modelica definition

encapsulated model Set_v_start "Set v_start"
  import Modelica;
  extends Modelica.Blocks.Interfaces.BlockIcon;
  Modelica.Blocks.Interfaces.RealInput v_start "Start velocity";

  Modelica.Mechanics.Translational.Interfaces.Flange_b flange;
initial equation 
  der(flange.s) = v_start;
equation 
  flange.f = 0;
end Set_v_start;

---

Modelica.Mechanics.Translational.Components.InitializeFlange.Set_a_start

Set a_start

Information

Extends from Modelica.Blocks.Interfaces.BlockIcon (Basic graphical layout of input/output block).

Connectors

Type	Name	Description
input RealInput	a_start	Start acceleration
Flange_b	flange

Modelica definition

encapsulated model Set_a_start "Set a_start"
  import Modelica;
  extends Modelica.Blocks.Interfaces.BlockIcon;
  Modelica.Blocks.Interfaces.RealInput a_start "Start acceleration";

  Modelica.Mechanics.Translational.Interfaces.Flange_b flange(s(stateSelect=StateSelect.avoid));
  Modelica.SIunits.Velocity v = der(flange.s);
initial equation 
  der(v) = a_start;
equation 
  flange.f = 0;
end Set_a_start;

---

Modelica.Mechanics.Translational.Components.InitializeFlange.Set_flange_f

Set flange_f to zero

Information

Extends from Modelica.Blocks.Interfaces.BlockIcon (Basic graphical layout of input/output block).

Connectors

Type	Name	Description
Flange_b	flange

Modelica definition

encapsulated model Set_flange_f "Set flange_f to zero"
  import Modelica;
  extends Modelica.Blocks.Interfaces.BlockIcon;
  Modelica.Mechanics.Translational.Interfaces.Flange_b flange;
equation 
  flange.f = 0;
end Set_flange_f;

---

Modelica.Mechanics.Translational.Components.MassWithStopAndFriction.PartialFrictionWithStop

Base model of Coulomb friction elements with stop

Information

Basic model for Coulomb friction that models the stuck phase in a reliable way.
Additionally, a left and right stop are handled.

Extends from PartialRigid (Rigid connection of two translational 1D flanges ).

Parameters

Type	Name	Default	Description
Position	smax		Right stop for (right end of) sliding mass [m]
Position	smin		Left stop for (left end of) sliding mass [m]
Length	L		Length of component, from left flange to right flange (= flange_b.s - flange_a.s) [m]
Advanced
Velocity	v_small	1e-3	Relative velocity near to zero (see model info text) [m/s]

Connectors

Type	Name	Description
Flange_a	flange_a	Left flange of translational component
Flange_b	flange_b	Right flange of translational component

Modelica definition

encapsulated partial model PartialFrictionWithStop 
  "Base model of Coulomb friction elements with stop"

    import SI = Modelica.SIunits;
    import Modelica.Mechanics.Translational.Interfaces.PartialRigid;
  parameter SI.Position smax(start= 25) 
    "Right stop for (right end of) sliding mass";
  parameter SI.Position smin(start=-25) 
    "Left stop for (left end of) sliding mass";
  parameter SI.Velocity v_small=1e-3 
    "Relative velocity near to zero (see model info text)";
// Equations to define the following variables have to be defined in subclasses
  SI.Velocity v_relfric "Relative velocity between frictional surfaces";
  SI.Acceleration a_relfric "Relative acceleration between frictional surfaces";
  SI.Force f 
    "Friction force (positive, if directed in opposite direction of v_rel)";
  SI.Force f0 "Friction force for v=0 and forward sliding";
  SI.Force f0_max "Maximum friction force for v=0 and locked";
  Boolean free "true, if frictional element is not active";
// Equations to define the following variables are given in this class
  Real sa(unit="1") 
    "Path parameter of friction characteristic f = f(a_relfric)";
  Boolean startForward(start=false, fixed=true) 
    "= true, if v_rel=0 and start of forward sliding or v_rel > v_small";
  Boolean startBackward(start=false, fixed=true) 
    "= true, if v_rel=0 and start of backward sliding or v_rel < -v_small";
  Boolean locked(start=false) "true, if v_rel=0 and not sliding";
  extends PartialRigid(s(start=0, stateSelect = StateSelect.always));
  constant Integer Unknown=3 "Value of mode is not known";
  constant Integer Free=2 "Element is not active";
  constant Integer Forward=1 "v_rel > 0 (forward sliding)";
  constant Integer Stuck=0 
    "v_rel = 0 (forward sliding, locked or backward sliding)";
  constant Integer Backward=-1 "v_rel < 0 (backward sliding)";
  Integer mode(
    final min=Backward,
    final max=Unknown,
    start=Unknown, fixed=true);
protected 
  constant SI.Acceleration unitAcceleration = 1;
  constant SI.Force unitForce = 1;
equation 
/* Friction characteristic
   (locked is introduced to help the Modelica translator determining
   the different structural configurations,
   if for each configuration special code shall be generated)
*/
  startForward = pre(mode) == Stuck and (sa > f0_max/unitForce and s < (smax - L/2) or 
        pre(startForward) and sa > f0/unitForce and s < (smax - L/2)) or pre(mode)
     == Backward and v_relfric > v_small or initial() and (v_relfric > 0);
  startBackward = pre(mode) == Stuck and (sa < -f0_max/unitForce and s > (smin + L/2) or 
        pre(startBackward) and sa < -f0/unitForce and s > (smin + L/2)) or pre(mode)
     == Forward and v_relfric < -v_small or initial() and (v_relfric < 0);
  locked = not free and 
    not (pre(mode) == Forward or startForward or pre(mode) == Backward or startBackward);

  a_relfric/unitAcceleration = if locked then               0 else 
                               if free then                 sa else 
                               if startForward then         sa - f0_max/unitForce else 
                               if startBackward then        sa + f0_max/unitForce else 
                               if pre(mode) == Forward then sa - f0_max/unitForce else 
                                                            sa + f0_max/unitForce;

/* Friction torque has to be defined in a subclass. Example for a clutch:
   f = if locked then sa else
       if free then   0 else
       cgeo*fn*(if startForward then          Math.tempInterpol1( v_relfric, mue_pos, 2) else
                if startBackward then        -Math.tempInterpol1(-v_relfric, mue_pos, 2) else
                if pre(mode) == Forward then  Math.tempInterpol1( v_relfric, mue_pos, 2) else
                                             -Math.tempInterpol1(-v_relfric, mue_pos, 2));
*/
// finite state machine to determine configuration
  mode = if free then Free else 
    (if (pre(mode) == Forward  or pre(mode) == Free or startForward)  and v_relfric > 0 and s < (smax - L/2) then 
       Forward else 
     if (pre(mode) == Backward or pre(mode) == Free or startBackward) and v_relfric < 0 and s > (smin + L/2) then 
       Backward else 
       Stuck);
end PartialFrictionWithStop;

---

HTML-documentation generated by Dymola Sun Jan 17 21:11:49 2010.