Modelica.Mechanics.Translational.Examples

Information

This package contains example models to demonstrate the usage of the Translational package. Open the models and simulate them according to the provided description in the models.

Extends from Modelica.Icons.Library (Icon for library).

Package Content

Name	Description
SignConvention	Examples for the used sign conventions.
InitialConditions	Setting of initial conditions
WhyArrows	Use of arrows in Mechanics.Translational
Accelerate	Use of model accelerate.
Damper	Use of damper models.
Oscillator	Oscillator demonstrates the use of initial conditions.
Sensors	Sensors for translational systems.
Friction	Use of model Stop
PreLoad	Preload of a spool using ElastoGap models.
ElastoGap	Demonstrate usage of ElastoGap
Brake	Demonstrate braking of a translational moving mass
Utilities	Utility classes used by the Example models

Modelica.Mechanics.Translational.Examples.SignConvention

Information

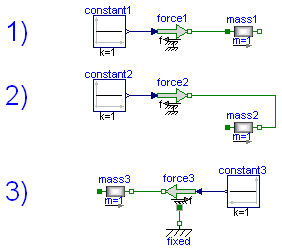
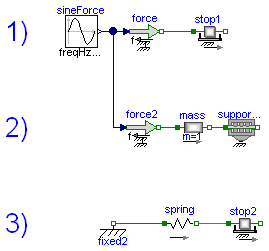
If all arrows point in the same direction a positive force results in a positive acceleration a, velocity v and position s.

        a = 1 m/s2
        v = 1 m/s after 1 s (SlidingMass1.v)
        s = 0.5 m after 1 s (SlidingMass1.s)

It is of course possible to ignore the arrows and connect the models in an arbitrary way. But then it is hard see in what direction the force acts.

In the third system the two arrows are opposed which means that the force acts in the opposite direction (in the same direction as in the two other examples).

Extends from Modelica.Icons.Example (Icon for an example model).

Modelica definition

model SignConvention "Examples for the used sign conventions."
  extends Modelica.Icons.Example;
  Translational.Components.Mass mass1(L=1,
    s(fixed=true),
    v(fixed=true),
    m=1);
  Translational.Sources.Force force1;
  Modelica.Blocks.Sources.Constant constant1(k=1);
  Translational.Components.Mass mass2(L=1,
    s(fixed=true),
    v(fixed=true),
    m=1);
  Translational.Sources.Force force2;
  Modelica.Blocks.Sources.Constant constant2(k=1);
  Translational.Components.Mass mass3(L=1,
    s(fixed=true),
    v(fixed=true),
    m=1);
  Translational.Sources.Force force3(useSupport=true);
  Modelica.Blocks.Sources.Constant constant3(k=1);
  Translational.Components.Fixed fixed;
equation 
  connect(constant1.y,force1. f);
  connect(constant2.y,force2. f);
  connect(constant3.y,force3. f);
  connect(force1.flange, mass1.flange_a);
  connect(force2.flange, mass2.flange_b);
  connect(mass3.flange_b, force3.flange);
  connect(fixed.flange, force3.support);
end SignConvention;

Modelica.Mechanics.Translational.Examples.InitialConditions

Information

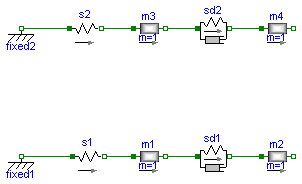
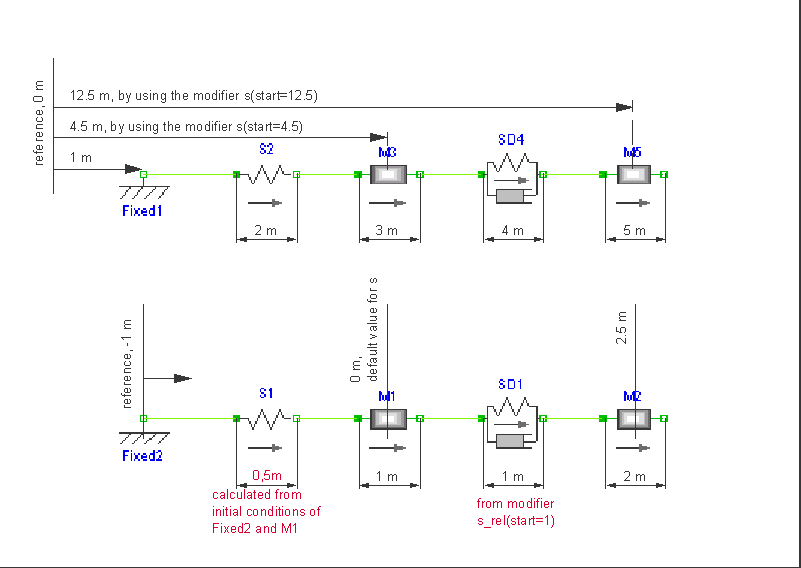
There are several ways to set initial conditions. In the first system the position of the mass m3 was defined by using the modifier s(start=4.5), the position of m4 by s(start=12.5). These positions were chosen such that the system is a rest. To calculate these values start at the left (Fixed1) with a value of 1 m. The spring has an unstreched length of 2 m and m3 an length of 3 m, which leads to

        1   m (fixed1)
      + 2   m (spring s2)
      + 3/2 m (half of the length of mass m3)
      -------
        4,5 m = s(start = 4.5) for m3
      + 3/2 m (half of the length of mass m3)
      + 4   m (springDamper 2)
      + 5/2 m (half of length of mass m4)
      -------
       12,5 m = s(start = 12.5) for m4

This selection of initial conditions has the effect that Dymola selects those variables (m3.s and m4.s) as state variables. In the second example the length of the springs are given as start values but they cannot be used as state for pure springs (only for the spring/damper combination). In this case the system is not at rest.

Extends from Modelica.Icons.Example (Icon for an example model).

Modelica definition

model InitialConditions "Setting of initial conditions"

  extends Modelica.Icons.Example;

  Translational.Components.Fixed fixed2(        s0=1);
  Translational.Components.Spring s2(        s_rel0=2, c=1e3);
  Translational.Components.Mass m3(           L=3, s(start=4.5, fixed=true),
    v(fixed=true),
    m=1);
  Translational.Components.SpringDamper sd2(        s_rel0=4, c=111,
    d=1);
  Translational.Components.Mass m4(           L=5, s(start=12.5, fixed=true),
    v(fixed=true),
    m=1);

  Translational.Components.Fixed fixed1(        s0=-1);
  Translational.Components.Spring s1(
    s_rel0=1,
    c=1e3,
    s_rel(start=1, fixed=true));
  Translational.Components.Mass m1(           L=1, v(fixed=true),
    m=1);
  Translational.Components.SpringDamper sd1(
    s_rel0=1,
    c=111,
    s_rel(start=1, fixed=true),
    v_rel(fixed=true),
    d=1);
  Translational.Components.Mass m2(           L=2, m=1);
equation 
  connect(s2.flange_a, fixed2.flange);
  connect(s1.flange_a, fixed1.flange);
  connect(m1.flange_a, s1.flange_b);
  connect(sd1.flange_a, m1.flange_b);
  connect(m2.flange_a, sd1.flange_b);
  connect(m4.flange_a, sd2.flange_b);
  connect(sd2.flange_a, m3.flange_b);
  connect(m3.flange_a, s2.flange_b);
end InitialConditions;

Modelica.Mechanics.Translational.Examples.WhyArrows

Information

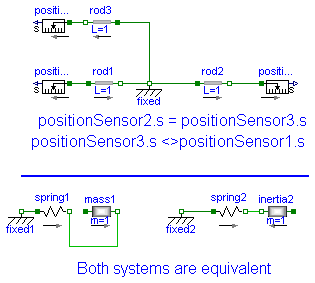
When using the models of the translational sublibrary it is recommended to make sure that all arrows point in the same direction because then all component have the same reference system. In the example the distance from flange_a of Rod1 to flange_b of Rod2 is 2 m. The distance from flange_a of Rod1 to flange_b of Rod3 is also 2 m though it is difficult to see that. Without the arrows it would be almost impossible to notice. That all arrows point in the same direction is a sufficient condition for an easy use of the library. There are cases where horizontally flipped models can be used without problems.

Extends from Modelica.Icons.Example (Icon for an example model).

Modelica definition

model WhyArrows "Use of arrows in Mechanics.Translational"

  extends Modelica.Icons.Example;

  Translational.Components.Fixed fixed;
  Translational.Components.Rod rod1(        L=1);
  Translational.Components.Rod rod2(        L=1);
  Translational.Components.Rod rod3(        L=1);
  Translational.Sensors.PositionSensor positionSensor2;
  Translational.Sensors.PositionSensor positionSensor1;
  Translational.Sensors.PositionSensor positionSensor3;
  Translational.Components.Fixed fixed1(        s0=-1.9);
  Translational.Components.Spring spring1(        s_rel0=2, c=11);
  Translational.Components.Mass mass1(
    L=2,
    s(fixed=true),
    v(fixed=true),
    m=1);
  Translational.Components.Fixed fixed2(        s0=-1.9);
  Translational.Components.Spring spring2(        s_rel0=2, c=11);
  Translational.Components.Mass inertia2(           L=2,
    m=1,
    s(fixed=true),
    v(fixed=true));
equation 
  connect(spring1.flange_b, mass1.flange_b);
  connect(spring2.flange_b, inertia2.flange_b);
  connect(rod3.flange_b,positionSensor3. flange);
  connect(rod1.flange_a,positionSensor1. flange);
  connect(rod1.flange_b, fixed.flange);
  connect(rod3.flange_a, fixed.flange);
  connect(fixed.flange, rod2.flange_a);
  connect(rod2.flange_b,positionSensor2. flange);
  connect(fixed1.flange,spring1. flange_a);
  connect(fixed2.flange,spring2. flange_a);
end WhyArrows;

Modelica.Mechanics.Translational.Examples.Accelerate

Information

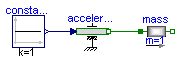
Demonstrate usage of component Sources.Accelerate by moving a massing with a predefined acceleration.

Extends from Modelica.Icons.Example (Icon for an example model).

Modelica definition

model Accelerate "Use of model accelerate."

  extends Modelica.Icons.Example;
  Translational.Sources.Accelerate accelerate;
  Translational.Components.Mass mass(L=1, m=1);
  Modelica.Blocks.Sources.Constant constantAcc(k=1);
equation 
  connect(accelerate.flange, mass.flange_a);
  connect(constantAcc.y, accelerate.a_ref);
end Accelerate;

Modelica.Mechanics.Translational.Examples.Damper

Information

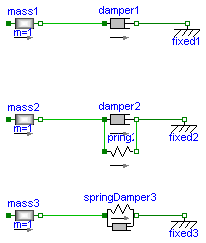
Demonstrate usage of damper components in different variants.

Extends from Modelica.Icons.Example (Icon for an example model).

Modelica definition

model Damper "Use of damper models."

  extends Modelica.Icons.Example;

  Translational.Components.Mass mass1(
    L=1,
    s(start=3, fixed=true),
    v(start=10, fixed=true),
    m=1);
  Translational.Components.Damper damper1(        d=25);
  Translational.Components.Fixed fixed1(        s0=4.5);
  Translational.Components.Mass mass2(
    L=1,
    s(start=3, fixed=true),
    v(start=10, fixed=true),
    m=1);
  Translational.Components.Damper damper2(        d=25);
  Translational.Components.Fixed fixed2(        s0=4.5);
  Translational.Components.Mass mass3(
    L=1,
    s(start=3, fixed=true),
    v(start=10, fixed=true),
    m=1);
  Translational.Components.Fixed fixed3(        s0=4.5);
  Translational.Components.Spring spring2(        s_rel0=1, c=1);
  Translational.Components.SpringDamper springDamper3(        s_rel0=1, d=25,
    c=1);
equation 
  connect(mass1.flange_b, damper1.flange_a);
  connect(mass2.flange_b, damper2.flange_a);
  connect(damper2.flange_b,spring2. flange_b);
  connect(damper2.flange_a,spring2. flange_a);
  connect(mass3.flange_b, springDamper3.flange_a);
  connect(damper1.flange_b, fixed1.flange);
  connect(damper2.flange_b, fixed2.flange);
  connect(springDamper3.flange_b, fixed3.flange);
end Damper;

Modelica.Mechanics.Translational.Examples.Oscillator

Information

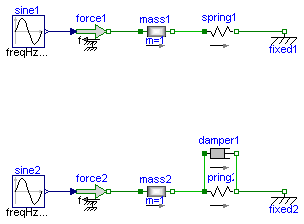
A spring - mass system is a mechanical oscillator. If no damping is included and the system is excited at resonance frequency infinite amplitudes will result. The resonant frequency is given by omega_res = sqrt(c / m) with:

      c spring stiffness
      m mass

To make sure that the system is initially at rest the initial conditions s(start=0) and v(start=0) for the SlindingMass are set. If damping is added the amplitudes are bounded.

Extends from Modelica.Icons.Example (Icon for an example model).

Modelica definition

model Oscillator 
  "Oscillator demonstrates the use of initial conditions."

  extends Modelica.Icons.Example;

  Translational.Components.Mass mass1(
    L=1,
    s(start=-0.5, fixed=true),
    v(start=0, fixed=true),
    m=1);
  Translational.Components.Spring spring1(        s_rel0=1, c=10000);
  Translational.Components.Fixed fixed1(        s0=1);
  Translational.Sources.Force force1;
  Modelica.Blocks.Sources.Sine sine1(freqHz=15.9155);
  Translational.Components.Mass mass2(
    L=1,
    s(start=-0.5, fixed=true),
    v(start=0, fixed=true),
    m=1);
  Translational.Components.Spring spring2(        s_rel0=1, c=10000);
  Translational.Components.Fixed fixed2(        s0=1);
  Translational.Sources.Force force2;
  Modelica.Blocks.Sources.Sine sine2(freqHz=15.9155);
  Translational.Components.Damper damper1(        d=10);
equation 
  connect(mass1.flange_b, spring1.flange_a);
  connect(spring2.flange_a,damper1. flange_a);
  connect(mass2.flange_b, spring2.flange_a);
  connect(damper1.flange_b,spring2. flange_b);
  connect(sine1.y,force1. f);
  connect(sine2.y,force2. f);
  connect(spring1.flange_b, fixed1.flange);
  connect(force2.flange, mass2.flange_a);
  connect(force1.flange, mass1.flange_a);
  connect(spring2.flange_b, fixed2.flange);
end Oscillator;

Modelica.Mechanics.Translational.Examples.Sensors

Information

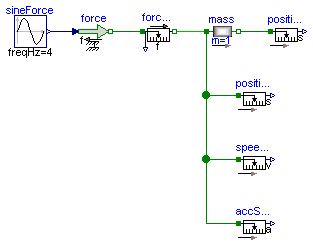
These sensors measure

   force f in N
   position s in m
   velocity v in m/s
   acceleration a in m/s2

Dhe measured velocity and acceleration is independent on the flange the sensor is connected to. The position depends on the flange (flange_a or flange_b) and the length L of the component. Plot PositionSensor1.s, PositionSensor2.s and SlidingMass1.s to see the difference.

Extends from Modelica.Icons.Example (Icon for an example model).

Modelica definition

model Sensors "Sensors for translational systems."

  extends Modelica.Icons.Example;

  Translational.Sensors.ForceSensor forceSensor;
  Translational.Sensors.SpeedSensor speedSensor1;
  Translational.Sensors.PositionSensor positionSensor1;
  Translational.Sensors.AccSensor accSensor1;
  Translational.Components.Mass mass(L=1,
    s(fixed=true),
    v(fixed=true),
    m=1);
  Translational.Sources.Force force;
  Modelica.Blocks.Sources.Sine sineForce(amplitude=10, freqHz=4);
  Translational.Sensors.PositionSensor positionSensor2;
equation 
  connect(forceSensor.flange_b, mass.flange_a);
  connect(sineForce.y, force.f);
  connect(forceSensor.flange_a, force.flange);
  connect(mass.flange_a, positionSensor1.flange);
  connect(mass.flange_a, speedSensor1.flange);
  connect(mass.flange_a, accSensor1.flange);
  connect(mass.flange_b, positionSensor2.flange);
end Sensors;

Modelica.Mechanics.Translational.Examples.Friction

Information

1. Simulate and then plot stop1.f as a function of stop1.v This gives the Stribeck curve.
2. The same model is also available by modeling the system with a Mass and a SupportFriction model. The SupportFriction model defines the friction characteristic with a table. The table is constructed with function Examples.Utilities.GenerateStribeckFrictionTable(..) to generate the same friction characteristic as with stop1. The simulation results of stop1 and of model mass are therefore identical.
3. Model stop2 gives an example for a hard stop. However there can arise some problems with the used modeling approach (use of reinit(..), convergence problems). In this case use the ElastoGap to model a stop (see example Preload).

Extends from Modelica.Icons.Example (Icon for an example model).

Modelica definition

model Friction "Use of model Stop"
  extends Modelica.Icons.Example;
  Modelica.Mechanics.Translational.Components.MassWithStopAndFriction stop1(
                                           L=1,
    s(fixed=true),
    v(fixed=true),
    smax=25,
    smin=-25,
    m=1,
    F_prop=1,
    F_Coulomb=5,
    F_Stribeck=10,
    fexp=2);
  Translational.Sources.Force force;
  Modelica.Blocks.Sources.Sine sineForce(amplitude=25, freqHz=0.25);
  Modelica.Mechanics.Translational.Components.MassWithStopAndFriction stop2(
    L=1,
    smax=0.9,
    smin=-0.9,
    F_Coulomb=3,
    F_Stribeck=5,
    s(start=0, fixed=true),
    m=1,
    F_prop=1,
    fexp=2,
    v(start=-5, fixed=true));
  Translational.Components.Spring spring(s_rel0=1, c=500);
  Translational.Components.Fixed fixed2(s0=-1.75);
  Translational.Sources.Force force2;
  Components.Mass mass(
    m=1,
    L=1,
    s(fixed=true),
    v(fixed=true));
  Components.SupportFriction supportFriction(f_pos=
        Examples.Utilities.GenerateStribeckFrictionTable(
            F_prop=1,
            F_Coulomb=5,
            F_Stribeck=10,
            fexp=2,
            v_max=12,
            nTable=50));
equation 
  connect(spring.flange_b, stop2.flange_a);
  connect(sineForce.y, force.f);
  connect(spring.flange_a, fixed2.flange);
  connect(force.flange, stop1.flange_a);
  connect(force2.flange, mass.flange_a);
  connect(mass.flange_b, supportFriction.flange_a);
  connect(sineForce.y, force2.f);
end Friction;

Modelica.Mechanics.Translational.Examples.PreLoad

Information

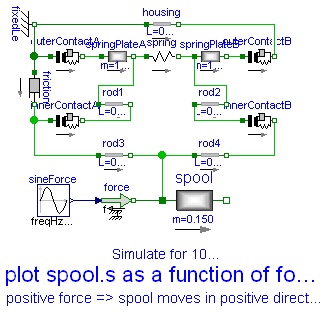
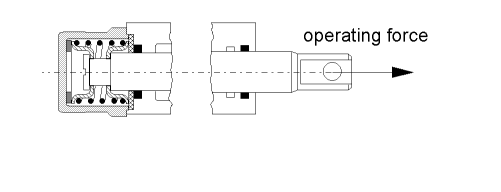
When designing hydraulic valves it is often necessary to hold the spool in a certain position as long as an external force is below a threshold value. If this force exceeds the treshold value a linear relation between force and position is desired. There are designs that need only one spring to accomplish this task. Using the ElastoGap elements this design can be modelled easily. Drawing of spool.

<

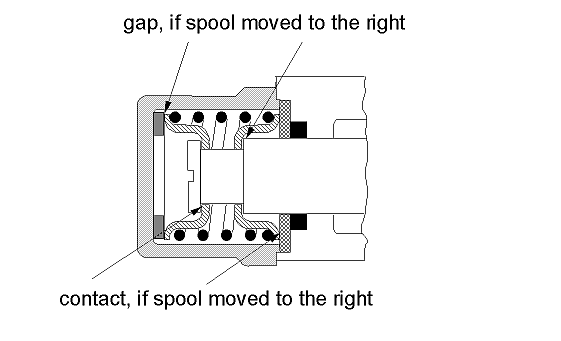
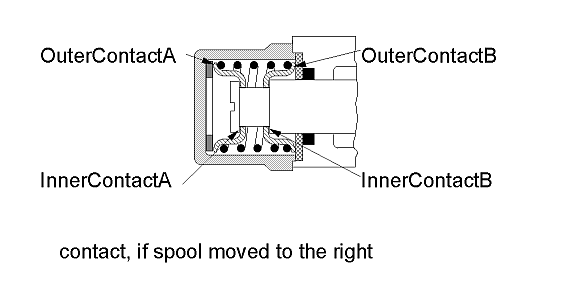
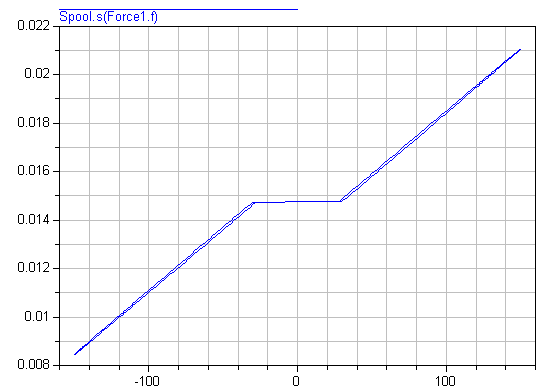
Spool position s as a function of working force f.

Extends from Modelica.Icons.Example (Icon for an example model).

Modelica definition

model PreLoad "Preload of a spool using ElastoGap models."

  extends Modelica.Icons.Example;

  Translational.Components.ElastoGap innerContactA(
    c=1000e3,
    d=250,
    s_rel0=0.001);
  Translational.Components.ElastoGap innerContactB(
    c=1000e3,
    d=250,
    s_rel0=0.001);
  Translational.Components.Mass spool(
    L=0.19,
    m=0.150,
    s(start=0.01475, fixed=true),
    v(fixed=true));
  Translational.Components.Fixed fixedLe(        s0=-0.0955);
  Translational.Components.Mass springPlateA(
    m=10e-3,
    L=0.002,
    s(start=-0.093, fixed=true),
    v(fixed=true));
  Translational.Components.Mass springPlateB(
    m=10e-3,
    s(start=-0.06925, fixed=true),
    L=0.002,
    v(fixed=true));
  Translational.Components.Spring spring(        c=20e3, s_rel0=0.025);
  Translational.Components.ElastoGap outerContactA(
    c=1000e3,
    d=250,
    s_rel0=0.0015);
  Translational.Components.ElastoGap outerContactB(
    c=1000e3,
    d=250,
    s_rel0=0.0015);
  Translational.Components.Rod rod1(        L=0.007);
  Translational.Components.Damper friction(        d=2500);
  Translational.Sources.Force force;
  Translational.Components.Rod housing(        L=0.0305);
  Translational.Components.Rod rod3(        L=0.00575);
  Translational.Components.Rod rod4(        L=0.00575);
  Translational.Components.Rod rod2(        L=0.007);
  Modelica.Blocks.Sources.Sine sineForce(amplitude=150, freqHz=0.01);
equation 
  connect(outerContactA.flange_b,springPlateA. flange_a);
  connect(springPlateA.flange_b,spring. flange_a);
  connect(spring.flange_b,springPlateB. flange_a);
  connect(springPlateB.flange_b,outerContactB. flange_a);
  connect(outerContactB.flange_b,housing. flange_b);
  connect(springPlateA.flange_b,rod1. flange_a);
  connect(innerContactA.flange_a,rod3. flange_a);
  connect(innerContactA.flange_b,rod1. flange_b);
  connect(rod2.flange_a,innerContactB. flange_a);
  connect(rod4.flange_b,innerContactB. flange_b);
  connect(friction.flange_b,rod3. flange_a);
  connect(rod3.flange_b,rod4. flange_a);
  connect(rod2.flange_b,springPlateB. flange_a);
  connect(spool.flange_a,rod4. flange_a);
  connect(sineForce.y, force.f);
  connect(force.flange, spool.flange_a);
  connect(outerContactA.flange_a, fixedLe.flange);
  connect(housing.flange_a, fixedLe.flange);
  connect(friction.flange_a, fixedLe.flange);
end PreLoad;

Modelica.Mechanics.Translational.Examples.ElastoGap

Information

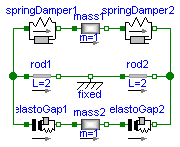
This model demonstrates the effect of ElastoGaps on eigenfrequency:
Plot mass1.s and mass2.s as well as mass1.v and mass2.v

mass1 is moved by both spring forces all the time.
Since elastoGap1 lifts off at s > -0.5 m and elastoGap2 lifts off s < +0.5 m, mass2 moves freely as long as -0.5 m < s < +0.5 m.

Extends from Modelica.Icons.Example (Icon for an example model).

Parameters

Type	Name	Default	Description
TranslationalDampingConstant	d	1.5	damping constant [N.s/m]

Modelica definition

model ElastoGap "Demonstrate usage of ElastoGap"
extends Modelica.Icons.Example;
  Components.Fixed fixed;
  Components.Rod rod1(L=2);
  Components.Rod rod2(L=2);
  Components.SpringDamper springDamper1(
    c=10,
    s_rel0=1,
    s_rel(fixed=false, start=1),
    d=1.5);
  Components.SpringDamper springDamper2(
    c=10,
    s_rel0=1,
    s_rel(fixed=false, start=1),
    d=1.5);
  Components.Mass mass1(
    s(fixed=true, start=2),
    L=0,
    m=1,
    v(fixed=true));
  Components.ElastoGap elastoGap1(
    c=10,
    s_rel(fixed=false, start=1.5),
    s_rel0=1.5,
    d=1.5);
  Components.ElastoGap elastoGap2(
    c=10,
    s_rel(fixed=false, start=1.5),
    s_rel0=1.5,
    d=1.5);
  Components.Mass mass2(
    s(fixed=true, start=2),
    L=0,
    m=1,
    v(fixed=true));
  parameter SI.TranslationalDampingConstant d=1.5 "damping constant";
equation 

  connect(rod1.flange_b, fixed.flange);
  connect(fixed.flange, rod2.flange_a);
  connect(springDamper1.flange_a, rod1.flange_a);
  connect(springDamper2.flange_b, rod2.flange_b);
  connect(springDamper1.flange_b, mass1.flange_a);
  connect(mass1.flange_b, springDamper2.flange_a);
  connect(rod1.flange_a, elastoGap1.flange_a);
  connect(rod2.flange_b, elastoGap2.flange_b);
  connect(elastoGap1.flange_b, mass2.flange_a);
  connect(mass2.flange_b, elastoGap2.flange_a);
end ElastoGap;

Modelica.Mechanics.Translational.Examples.Brake

Information

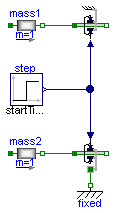
This model consists of a mass with an initial velocity of 1 m/s. After 0.1 s, a brake is activated and it is shown that the mass decelerates until it arrives at rest and remains at rest. Two versions of this system are present, one where the brake is implicitly grounded and one where it is explicitly grounded.

Extends from Modelica.Icons.Example (Icon for an example model).

Modelica definition

model Brake "Demonstrate braking of a translational moving mass"
  extends Modelica.Icons.Example;

  Modelica.Mechanics.Translational.Components.Brake brake(fn_max=1, useSupport=
        false);
  Modelica.Mechanics.Translational.Components.Mass mass1(m=1,
    s(fixed=true),
    v(start=1, fixed=true));
  Modelica.Blocks.Sources.Step step(startTime=0.1, height=2);
  Modelica.Mechanics.Translational.Components.Brake brake1(
                                                          fn_max=1, useSupport=
        true);
  Modelica.Mechanics.Translational.Components.Mass mass2(m=1,
    s(fixed=true),
    v(start=1, fixed=true));
  Modelica.Mechanics.Translational.Components.Fixed fixed;
equation 
  connect(mass1.flange_b, brake.flange_a);
  connect(step.y, brake.f_normalized);
  connect(mass2.flange_b, brake1.flange_a);
  connect(step.y, brake1.f_normalized);
  connect(fixed.flange, brake1.support);
end Brake;