Buildings.Fluid.Chillers
Package with chiller models
Information
This package contains component models for chillers.
Extends from Modelica.Icons.VariantsPackage (Icon for package containing variants).
Package Content
| Name | Description |
|---|---|
| Chiller with prescribed evaporator leaving temperature and performance curve adjusted based on Carnot efficiency | |
| Chiller with performance curve adjusted based on Carnot efficiency | |
| Electric chiller based on the DOE-2.1 model | |
| Electric chiller based on the DOE-2.1 model, but with performance as a function of condenser leaving instead of entering temperature | |
| Performance data for electric chillers | |
| Collection of models that illustrate model use and test models | |
| Collection of models that validate the chiller models | |
| Package with base classes for Buildings.Fluid.Chillers |
 Buildings.Fluid.Chillers.Carnot_TEva
Buildings.Fluid.Chillers.Carnot_TEva
Chiller with prescribed evaporator leaving temperature and performance curve adjusted based on Carnot efficiency
Information
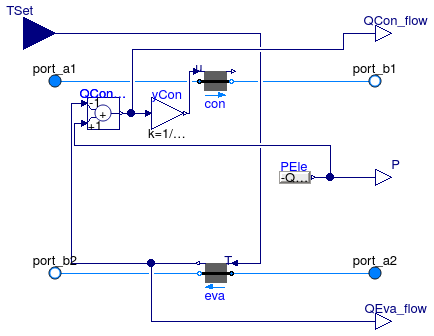
This is a model of a chiller whose coefficient of performance COP changes with temperatures in the same way as the Carnot efficiency changes. The control input is the setpoint of the evaporator leaving temperature, which is met exactly at steady state if the chiller has sufficient capacity.
The model allows to either specify the Carnot effectivness ηCarnot,0, or a COP0 at the nominal conditions, together with the evaporator temperature Teva,0 and the condenser temperature Tcon,0, in which case the model computes the Carnot effectivness as
ηCarnot,0 = COP0 ⁄ (Teva,0 ⁄ (Tcon,0-Teva,0)).
On the Advanced tab, a user can specify the temperatures that
will be used as the evaporator and condenser temperature.
During the simulation, the chiller COP is computed as the product
COP = ηCarnot,0 COPCarnot ηPL,
where COPCarnot is the Carnot efficiency and ηPL is a polynomial in the cooling part load ratio yPL that can be used to take into account a change in COP at part load conditions. This polynomial has the form
ηPL = a1 + a2 yPL + a3 yPL2 + ...
where the coefficients ai
are declared by the parameter a.
On the Dynamics tag, the model can be parametrized to compute a transient
or steady-state response.
The transient response of the model is computed using a first
order differential equation for the evaporator and condenser fluid volumes.
The chiller outlet temperatures are equal to the temperatures of these lumped volumes.
Typical use and important parameters
When using this component, make sure that the condenser has sufficient mass flow rate. Based on the evaporator mass flow rate, temperature difference and the efficiencies, the model computes how much heat will be added to the condenser. If the mass flow rate is too small, very high outlet temperatures can result.
The evaporator heat flow rate QEva_flow_nominal is used to assign
the default value for the mass flow rates, which are used for the pressure drop
calculations.
It is also used to compute the part load efficiency.
Hence, make sure that QEva_flow_nominal is set to a reasonable value.
The maximum cooling capacity is set by the parameter QEva_flow_min,
which is by default set to negative infinity.
The coefficient of performance depends on the evaporator and condenser leaving temperature since otherwise the second law of thermodynamics may be violated.
Notes
For a similar model that can be used as a heat pump, see Buildings.Fluid.HeatPumps.Examples.Carnot_TCon.
Extends from Buildings.Fluid.Chillers.BaseClasses.PartialCarnot_T (Partial model for chiller with performance curve adjusted based on Carnot efficiency).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| replaceable package Medium1 | PartialMedium | Medium 1 in the component | |
| replaceable package Medium2 | PartialMedium | Medium 2 in the component | |
| HeatFlowRate | QEva_flow_min | -Modelica.Constants.inf | Maximum heat flow rate for cooling (negative) [W] |
| Nominal condition | |||
| MassFlowRate | m1_flow_nominal | QCon_flow_nominal/cp1_defaul... | Nominal mass flow rate [kg/s] |
| MassFlowRate | m2_flow_nominal | QEva_flow_nominal/cp2_defaul... | Nominal mass flow rate [kg/s] |
| HeatFlowRate | QEva_flow_nominal | Nominal cooling heat flow rate (QEva_flow_nominal < 0) [W] | |
| HeatFlowRate | QCon_flow_nominal | -QEva_flow_nominal*(1 + COP_... | Nominal heating flow rate [W] |
| TemperatureDifference | dTEva_nominal | -10 | Temperature difference evaporator outlet-inlet [K] |
| TemperatureDifference | dTCon_nominal | 10 | Temperature difference condenser outlet-inlet [K] |
| Pressure | dp1_nominal | Pressure difference over condenser [Pa] | |
| Pressure | dp2_nominal | Pressure difference over evaporator [Pa] | |
| Efficiency | |||
| Boolean | use_eta_Carnot_nominal | true | Set to true to use Carnot effectiveness etaCarnot_nominal rather than COP_nominal |
| Real | etaCarnot_nominal | COP_nominal/(TUse_nominal/(T... | Carnot effectiveness (=COP/COP_Carnot) used if use_eta_Carnot_nominal = true [1] |
| Real | COP_nominal | etaCarnot_nominal*TUse_nomin... | Coefficient of performance at TEva_nominal and TCon_nominal, used if use_eta_Carnot_nominal = false [1] |
| Temperature | TCon_nominal | 303.15 | Condenser temperature used to compute COP_nominal if use_eta_Carnot_nominal=false [K] |
| Temperature | TEva_nominal | 278.15 | Evaporator temperature used to compute COP_nominal if use_eta_Carnot_nominal=false [K] |
| Real | a[:] | {1} | Coefficients for efficiency curve (need p(a=a, yPL=1)=1) |
| Assumptions | |||
| Boolean | allowFlowReversal1 | true | = false to simplify equations, assuming, but not enforcing, no flow reversal for medium 1 |
| Boolean | allowFlowReversal2 | true | = false to simplify equations, assuming, but not enforcing, no flow reversal for medium 2 |
| Advanced | |||
| MassFlowRate | m1_flow_small | 1E-4*abs(m1_flow_nominal) | Small mass flow rate for regularization of zero flow [kg/s] |
| MassFlowRate | m2_flow_small | 1E-4*abs(m2_flow_nominal) | Small mass flow rate for regularization of zero flow [kg/s] |
| Boolean | homotopyInitialization | true | = true, use homotopy method |
| Diagnostics | |||
| Boolean | show_T | false | = true, if actual temperature at port is computed |
| Flow resistance | |||
| Condenser | |||
| Boolean | from_dp1 | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | linearizeFlowResistance1 | false | = true, use linear relation between m_flow and dp for any flow rate |
| Real | deltaM1 | 0.1 | Fraction of nominal flow rate where flow transitions to laminar [1] |
| Evaporator | |||
| Boolean | from_dp2 | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | linearizeFlowResistance2 | false | = true, use linear relation between m_flow and dp for any flow rate |
| Real | deltaM2 | 0.1 | Fraction of nominal flow rate where flow transitions to laminar [1] |
| Dynamics | |||
| Condenser | |||
| Time | tau1 | 60 | Time constant at nominal flow rate (used if energyDynamics1 <> Modelica.Fluid.Types.Dynamics.SteadyState) [s] |
| Temperature | T1_start | Medium1.T_default | Initial or guess value of set point [K] |
| Evaporator | |||
| Time | tau2 | 60 | Time constant at nominal flow rate (used if energyDynamics2 <> Modelica.Fluid.Types.Dynamics.SteadyState) [s] |
| Temperature | T2_start | Medium2.T_default | Initial or guess value of set point [K] |
| Evaporator and condenser | |||
| Dynamics | energyDynamics | Modelica.Fluid.Types.Dynamic... | Type of energy balance: dynamic (3 initialization options) or steady state |
Connectors
| Type | Name | Description |
|---|---|---|
| FluidPort_a | port_a1 | Fluid connector a1 (positive design flow direction is from port_a1 to port_b1) |
| FluidPort_b | port_b1 | Fluid connector b1 (positive design flow direction is from port_a1 to port_b1) |
| FluidPort_a | port_a2 | Fluid connector a2 (positive design flow direction is from port_a2 to port_b2) |
| FluidPort_b | port_b2 | Fluid connector b2 (positive design flow direction is from port_a2 to port_b2) |
| output RealOutput | QCon_flow | Actual heating heat flow rate added to fluid 1 [W] |
| output RealOutput | P | Electric power consumed by compressor [W] |
| output RealOutput | QEva_flow | Actual cooling heat flow rate removed from fluid 2 [W] |
| input RealInput | TSet | Evaporator leaving water temperature [K] |
Modelica definition
 Buildings.Fluid.Chillers.Carnot_y
Buildings.Fluid.Chillers.Carnot_y
Chiller with performance curve adjusted based on Carnot efficiency
Information
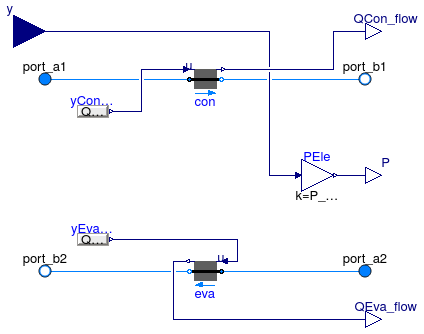
This is model of a chiller whose coefficient of performance COP changes with temperatures in the same way as the Carnot efficiency changes. The input signal y is the control signal for the compressor.
The model allows to either specify the Carnot effectivness ηCarnot,0, or a COP0 at the nominal conditions, together with the evaporator temperature Teva,0 and the condenser temperature Tcon,0, in which case the model computes the Carnot effectivness as
ηCarnot,0 = COP0 ⁄ (Teva,0 ⁄ (Tcon,0-Teva,0)).
The chiller COP is computed as the product
COP = ηCarnot,0 COPCarnot ηPL,
where COPCarnot is the Carnot efficiency and ηPL is a polynomial in the cooling part load ratio yPL that can be used to take into account a change in COP at part load conditions. This polynomial has the form
ηPL = a1 + a2 yPL + a3 yPL2 + ...
where the coefficients ai
are declared by the parameter a.
On the Dynamics tag, the model can be parametrized to compute a transient
or steady-state response.
The transient response of the model is computed using a first
order differential equation for the evaporator and condenser fluid volumes.
The chiller outlet temperatures are equal to the temperatures of these lumped volumes.
Typical use and important parameters
When using this component, make sure that the evaporator and the condenser have sufficient mass flow rate. Based on the mass flow rates, the compressor power, temperature difference and the efficiencies, the model computes how much heat will be added to the condenser and removed at the evaporator. If the mass flow rates are too small, very high temperature differences can result.
The evaporator heat flow rate QEva_flow_nominal is used to assign
the default value for the mass flow rates, which are used for the pressure drop
calculations.
It is also used to compute the part load efficiency.
Hence, make sure that QEva_flow_nominal is set to a reasonable value.
The maximum cooling capacity is set by the parameter QEva_flow_min,
which is by default set to negative infinity.
The coefficient of performance depends on the evaporator and condenser leaving temperature since otherwise the second law of thermodynamics may be violated.
Notes
For a similar model that can be used as a heat pump, see Buildings.Fluid.HeatPumps.Carnot_y.
Extends from Buildings.Fluid.Chillers.BaseClasses.PartialCarnot_y (Partial chiller model with performance curve adjusted based on Carnot efficiency).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| replaceable package Medium1 | PartialMedium | Medium 1 in the component | |
| replaceable package Medium2 | PartialMedium | Medium 2 in the component | |
| Nominal condition | |||
| MassFlowRate | m1_flow_nominal | QCon_flow_nominal/cp1_defaul... | Nominal mass flow rate [kg/s] |
| MassFlowRate | m2_flow_nominal | QEva_flow_nominal/cp2_defaul... | Nominal mass flow rate [kg/s] |
| TemperatureDifference | dTEva_nominal | -10 | Temperature difference evaporator outlet-inlet [K] |
| TemperatureDifference | dTCon_nominal | 10 | Temperature difference condenser outlet-inlet [K] |
| Pressure | dp1_nominal | Pressure difference over condenser [Pa] | |
| Pressure | dp2_nominal | Pressure difference over evaporator [Pa] | |
| Power | P_nominal | Nominal compressor power (at y=1) [W] | |
| Efficiency | |||
| Boolean | use_eta_Carnot_nominal | true | Set to true to use Carnot effectiveness etaCarnot_nominal rather than COP_nominal |
| Real | etaCarnot_nominal | COP_nominal/(TUse_nominal/(T... | Carnot effectiveness (=COP/COP_Carnot) used if use_eta_Carnot_nominal = true [1] |
| Real | COP_nominal | etaCarnot_nominal*TUse_nomin... | Coefficient of performance at TEva_nominal and TCon_nominal, used if use_eta_Carnot_nominal = false [1] |
| Temperature | TCon_nominal | 303.15 | Condenser temperature used to compute COP_nominal if use_eta_Carnot_nominal=false [K] |
| Temperature | TEva_nominal | 278.15 | Evaporator temperature used to compute COP_nominal if use_eta_Carnot_nominal=false [K] |
| Real | a[:] | {1} | Coefficients for efficiency curve (need p(a=a, yPL=1)=1) |
| Assumptions | |||
| Boolean | allowFlowReversal1 | true | = false to simplify equations, assuming, but not enforcing, no flow reversal for medium 1 |
| Boolean | allowFlowReversal2 | true | = false to simplify equations, assuming, but not enforcing, no flow reversal for medium 2 |
| Advanced | |||
| MassFlowRate | m1_flow_small | 1E-4*abs(m1_flow_nominal) | Small mass flow rate for regularization of zero flow [kg/s] |
| MassFlowRate | m2_flow_small | 1E-4*abs(m2_flow_nominal) | Small mass flow rate for regularization of zero flow [kg/s] |
| Boolean | homotopyInitialization | true | = true, use homotopy method |
| Diagnostics | |||
| Boolean | show_T | false | = true, if actual temperature at port is computed |
| Flow resistance | |||
| Condenser | |||
| Boolean | from_dp1 | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | linearizeFlowResistance1 | false | = true, use linear relation between m_flow and dp for any flow rate |
| Real | deltaM1 | 0.1 | Fraction of nominal flow rate where flow transitions to laminar [1] |
| Evaporator | |||
| Boolean | from_dp2 | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | linearizeFlowResistance2 | false | = true, use linear relation between m_flow and dp for any flow rate |
| Real | deltaM2 | 0.1 | Fraction of nominal flow rate where flow transitions to laminar [1] |
| Dynamics | |||
| Condenser | |||
| Time | tau1 | 60 | Time constant at nominal flow rate (used if energyDynamics1 <> Modelica.Fluid.Types.Dynamics.SteadyState) [s] |
| Temperature | T1_start | Medium1.T_default | Initial or guess value of set point [K] |
| Evaporator | |||
| Time | tau2 | 60 | Time constant at nominal flow rate (used if energyDynamics2 <> Modelica.Fluid.Types.Dynamics.SteadyState) [s] |
| Temperature | T2_start | Medium2.T_default | Initial or guess value of set point [K] |
| Evaporator and condenser | |||
| Dynamics | energyDynamics | Modelica.Fluid.Types.Dynamic... | Type of energy balance: dynamic (3 initialization options) or steady state |
Connectors
| Type | Name | Description |
|---|---|---|
| FluidPort_a | port_a1 | Fluid connector a1 (positive design flow direction is from port_a1 to port_b1) |
| FluidPort_b | port_b1 | Fluid connector b1 (positive design flow direction is from port_a1 to port_b1) |
| FluidPort_a | port_a2 | Fluid connector a2 (positive design flow direction is from port_a2 to port_b2) |
| FluidPort_b | port_b2 | Fluid connector b2 (positive design flow direction is from port_a2 to port_b2) |
| output RealOutput | QCon_flow | Actual heating heat flow rate added to fluid 1 [W] |
| output RealOutput | P | Electric power consumed by compressor [W] |
| output RealOutput | QEva_flow | Actual cooling heat flow rate removed from fluid 2 [W] |
| input RealInput | y | Part load ratio of compressor [1] |
Modelica definition
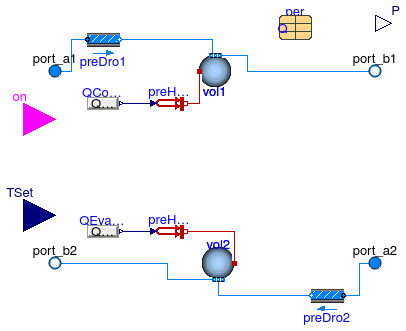
 Buildings.Fluid.Chillers.ElectricEIR
Buildings.Fluid.Chillers.ElectricEIR
Electric chiller based on the DOE-2.1 model
Information
Model of an electric chiller, based on the DOE-2.1 chiller model and
the EnergyPlus chiller model Chiller:Electric:EIR.
This model uses three functions to predict capacity and power consumption:
- A biquadratic function is used to predict cooling capacity as a function of condenser entering and evaporator leaving fluid temperature.
- A quadratic functions is used to predict power input to cooling capacity ratio with respect to the part load ratio.
- A biquadratic functions is used to predict power input to cooling capacity ratio as a function of condenser entering and evaporator leaving fluid temperature.
These curves are stored in the data record per and are available from
Buildings.Fluid.Chillers.Data.ElectricEIR.
Additional performance curves can be developed using
two available techniques (Hydeman and Gillespie, 2002). The first technique is called the
Least-squares Linear Regression method and is used when sufficient performance data exist
to employ standard least-square linear regression techniques. The second technique is called
Reference Curve Method and is used when insufficient performance data exist to apply linear
regression techniques. A detailed description of both techniques can be found in
Hydeman and Gillespie (2002).
The model takes as an input the set point for the leaving chilled water temperature, which is met if the chiller has sufficient capacity. Thus, the model has a built-in, ideal temperature control. The model has three tests on the part load ratio and the cycling ratio:
-
The test
PLR1 =min(QEva_flow_set/QEva_flow_ava, per.PLRMax);
ensures that the chiller capacity does not exceed the chiller capacity specified by the parameterper.PLRMax. -
The test
CR = min(PLR1/per.PRLMin, 1.0);
computes a cycling ratio. This ratio expresses the fraction of time that a chiller would run if it were to cycle because its load is smaller than the minimal load at which it can operate. Note that this model continuously operates even if the part load ratio is below the minimum part load ratio. Its leaving evaporator and condenser temperature can therefore be considered as an average temperature between the modes where the compressor is off and on. -
The test
PLR2 = max(per.PLRMinUnl, PLR1);
computes the part load ratio of the compressor. The assumption is that for a part load ratio belowper.PLRMinUnl, the chiller uses hot gas bypass to reduce the capacity, while the compressor power draw does not change.
The electric power only contains the power for the compressor, but not any power for pumps or fans.
The model can be parametrized to compute a transient or steady-state response. The transient response of the boiler is computed using a first order differential equation for the evaporator and condenser fluid volumes. The chiller outlet temperatures are equal to the temperatures of these lumped volumes.
References
- Hydeman, M. and K.L. Gillespie. 2002. Tools and Techniques to Calibrate Electric Chiller Component Models. ASHRAE Transactions, AC-02-9-1.
Extends from Buildings.Fluid.Chillers.BaseClasses.PartialElectric (Partial model for electric chiller based on the model in DOE-2, CoolTools and EnergyPlus).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| replaceable package Medium1 | PartialMedium | Medium 1 in the component | |
| replaceable package Medium2 | PartialMedium | Medium 2 in the component | |
| Generic | per | Performance data | |
| Nominal condition | |||
| MassFlowRate | m1_flow_nominal | mCon_flow_nominal | Nominal mass flow rate [kg/s] |
| MassFlowRate | m2_flow_nominal | mEva_flow_nominal | Nominal mass flow rate [kg/s] |
| PressureDifference | dp1_nominal | Pressure difference [Pa] | |
| PressureDifference | dp2_nominal | Pressure difference [Pa] | |
| Initialization | |||
| Real | capFunT.start | 1 | Cooling capacity factor function of temperature curve [1] |
| Efficiency | EIRFunT.start | 1 | Power input to cooling capacity ratio function of temperature curve [1] |
| Efficiency | EIRFunPLR.start | 1 | Power input to cooling capacity ratio function of part load ratio [1] |
| Real | PLR1.start | 1 | Part load ratio [1] |
| Real | PLR2.start | 1 | Part load ratio [1] |
| Real | CR.start | 1 | Cycling ratio [1] |
| Assumptions | |||
| Boolean | allowFlowReversal1 | true | = false to simplify equations, assuming, but not enforcing, no flow reversal for medium 1 |
| Boolean | allowFlowReversal2 | true | = false to simplify equations, assuming, but not enforcing, no flow reversal for medium 2 |
| Advanced | |||
| MassFlowRate | m1_flow_small | 1E-4*abs(m1_flow_nominal) | Small mass flow rate for regularization of zero flow [kg/s] |
| MassFlowRate | m2_flow_small | 1E-4*abs(m2_flow_nominal) | Small mass flow rate for regularization of zero flow [kg/s] |
| Boolean | homotopyInitialization | true | = true, use homotopy method |
| Diagnostics | |||
| Boolean | show_T | false | = true, if actual temperature at port is computed |
| Flow resistance | |||
| Medium 1 | |||
| Boolean | from_dp1 | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | linearizeFlowResistance1 | false | = true, use linear relation between m_flow and dp for any flow rate |
| Real | deltaM1 | 0.1 | Fraction of nominal flow rate where flow transitions to laminar |
| Medium 2 | |||
| Boolean | from_dp2 | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | linearizeFlowResistance2 | false | = true, use linear relation between m_flow and dp for any flow rate |
| Real | deltaM2 | 0.1 | Fraction of nominal flow rate where flow transitions to laminar |
| Dynamics | |||
| Nominal condition | |||
| Time | tau1 | 30 | Time constant at nominal flow [s] |
| Time | tau2 | 30 | Time constant at nominal flow [s] |
| Equations | |||
| Dynamics | energyDynamics | Modelica.Fluid.Types.Dynamic... | Type of energy balance: dynamic (3 initialization options) or steady state |
| Dynamics | massDynamics | energyDynamics | Type of mass balance: dynamic (3 initialization options) or steady state |
| Initialization | |||
| Medium 1 | |||
| AbsolutePressure | p1_start | Medium1.p_default | Start value of pressure [Pa] |
| Temperature | T1_start | 273.15 + 25 | Start value of temperature [K] |
| MassFraction | X1_start[Medium1.nX] | Medium1.X_default | Start value of mass fractions m_i/m [kg/kg] |
| ExtraProperty | C1_start[Medium1.nC] | fill(0, Medium1.nC) | Start value of trace substances |
| ExtraProperty | C1_nominal[Medium1.nC] | fill(1E-2, Medium1.nC) | Nominal value of trace substances. (Set to typical order of magnitude.) |
| Medium 2 | |||
| AbsolutePressure | p2_start | Medium2.p_default | Start value of pressure [Pa] |
| Temperature | T2_start | 273.15 + 5 | Start value of temperature [K] |
| MassFraction | X2_start[Medium2.nX] | Medium2.X_default | Start value of mass fractions m_i/m [kg/kg] |
| ExtraProperty | C2_start[Medium2.nC] | fill(0, Medium2.nC) | Start value of trace substances |
| ExtraProperty | C2_nominal[Medium2.nC] | fill(1E-2, Medium2.nC) | Nominal value of trace substances. (Set to typical order of magnitude.) |
Connectors
| Type | Name | Description |
|---|---|---|
| FluidPort_a | port_a1 | Fluid connector a1 (positive design flow direction is from port_a1 to port_b1) |
| FluidPort_b | port_b1 | Fluid connector b1 (positive design flow direction is from port_a1 to port_b1) |
| FluidPort_a | port_a2 | Fluid connector a2 (positive design flow direction is from port_a2 to port_b2) |
| FluidPort_b | port_b2 | Fluid connector b2 (positive design flow direction is from port_a2 to port_b2) |
| input BooleanInput | on | Set to true to enable compressor, or false to disable compressor |
| input RealInput | TSet | Set point for leaving chilled water temperature [K] |
| output RealOutput | P | Electric power consumed by compressor [W] |
Modelica definition
 Buildings.Fluid.Chillers.ElectricReformulatedEIR
Buildings.Fluid.Chillers.ElectricReformulatedEIR
Electric chiller based on the DOE-2.1 model, but with performance as a function of condenser leaving instead of entering temperature

Information
Model of an electric chiller, based on the model by
Hydeman et al. (2002) that has been developed in the CoolTools project
and that is implemented in EnergyPlus as the model
Chiller:Electric:ReformulatedEIR.
This empirical model is similar to
Buildings.Fluid.Chillers.ElectricEIR.
The difference is that to compute the performance, this model
uses the condenser leaving temperature instead of the entering temperature,
and it uses a bicubic polynomial to compute the part load performance.
This model uses three functions to predict capacity and power consumption:
- A biquadratic function is used to predict cooling capacity as a function of condenser leaving and evaporator leaving fluid temperature.
- A bicubic function is used to predict power input to cooling capacity ratio as a function of condenser leaving temperature and part load ratio.
- A biquadratic functions is used to predict power input to cooling capacity ratio as a function of condenser leaving and evaporator leaving fluid temperature.
These curves are stored in the data record per and are available from
Buildings.Fluid.Chillers.Data.ElectricReformulatedEIRChiller.
Additional performance curves can be developed using
two available techniques (Hydeman and Gillespie, 2002). The first technique is called the
Least-squares Linear Regression method and is used when sufficient performance data exist
to employ standard least-square linear regression techniques. The second technique is called
Reference Curve Method and is used when insufficient performance data exist to apply linear
regression techniques. A detailed description of both techniques can be found in
Hydeman and Gillespie (2002).
The model takes as an input the set point for the leaving chilled water temperature, which is met if the chiller has sufficient capacity. Thus, the model has a built-in, ideal temperature control. The model has three tests on the part load ratio and the cycling ratio:
-
The test
PLR1 =min(QEva_flow_set/QEva_flow_ava, per.PLRMax);
ensures that the chiller capacity does not exceed the chiller capacity specified by the parameterper.PLRMax. -
The test
CR = min(PLR1/per.PRLMin, 1.0);
computes a cycling ratio. This ratio expresses the fraction of time that a chiller would run if it were to cycle because its load is smaller than the minimal load at which it can operate. Note that this model continuously operates even if the part load ratio is below the minimum part load ratio. Its leaving evaporator and condenser temperature can therefore be considered as an average temperature between the modes where the compressor is off and on. -
The test
PLR2 = max(per.PLRMinUnl, PLR1);
computes the part load ratio of the compressor. The assumption is that for a part load ratio belowper.PLRMinUnl, the chiller uses hot gas bypass to reduce the capacity, while the compressor power draw does not change.
The electric power only contains the power for the compressor, but not any power for pumps or fans.
The model can be parametrized to compute a transient or steady-state response. The transient response of the boiler is computed using a first order differential equation for the evaporator and condenser fluid volumes. The chiller outlet temperatures are equal to the temperatures of these lumped volumes.
References
- Hydeman, M., N. Webb, P. Sreedharan, and S. Blanc. 2002. Development and Testing of a Reformulated Regression-Based Electric Chiller Model. ASHRAE Transactions, HI-02-18-2.
- Hydeman, M. and K.L. Gillespie. 2002. Tools and Techniques to Calibrate Electric Chiller Component Models. ASHRAE Transactions, AC-02-9-1.
Extends from Buildings.Fluid.Chillers.BaseClasses.PartialElectric (Partial model for electric chiller based on the model in DOE-2, CoolTools and EnergyPlus).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| replaceable package Medium1 | PartialMedium | Medium 1 in the component | |
| replaceable package Medium2 | PartialMedium | Medium 2 in the component | |
| Generic | per | Performance data | |
| Nominal condition | |||
| MassFlowRate | m1_flow_nominal | mCon_flow_nominal | Nominal mass flow rate [kg/s] |
| MassFlowRate | m2_flow_nominal | mEva_flow_nominal | Nominal mass flow rate [kg/s] |
| PressureDifference | dp1_nominal | Pressure difference [Pa] | |
| PressureDifference | dp2_nominal | Pressure difference [Pa] | |
| Initialization | |||
| Real | capFunT.start | 1 | Cooling capacity factor function of temperature curve [1] |
| Efficiency | EIRFunT.start | 1 | Power input to cooling capacity ratio function of temperature curve [1] |
| Efficiency | EIRFunPLR.start | 1 | Power input to cooling capacity ratio function of part load ratio [1] |
| Real | PLR1.start | 1 | Part load ratio [1] |
| Real | PLR2.start | 1 | Part load ratio [1] |
| Real | CR.start | 1 | Cycling ratio [1] |
| Assumptions | |||
| Boolean | allowFlowReversal1 | true | = false to simplify equations, assuming, but not enforcing, no flow reversal for medium 1 |
| Boolean | allowFlowReversal2 | true | = false to simplify equations, assuming, but not enforcing, no flow reversal for medium 2 |
| Advanced | |||
| MassFlowRate | m1_flow_small | 1E-4*abs(m1_flow_nominal) | Small mass flow rate for regularization of zero flow [kg/s] |
| MassFlowRate | m2_flow_small | 1E-4*abs(m2_flow_nominal) | Small mass flow rate for regularization of zero flow [kg/s] |
| Boolean | homotopyInitialization | true | = true, use homotopy method |
| Diagnostics | |||
| Boolean | show_T | false | = true, if actual temperature at port is computed |
| Flow resistance | |||
| Medium 1 | |||
| Boolean | from_dp1 | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | linearizeFlowResistance1 | false | = true, use linear relation between m_flow and dp for any flow rate |
| Real | deltaM1 | 0.1 | Fraction of nominal flow rate where flow transitions to laminar |
| Medium 2 | |||
| Boolean | from_dp2 | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | linearizeFlowResistance2 | false | = true, use linear relation between m_flow and dp for any flow rate |
| Real | deltaM2 | 0.1 | Fraction of nominal flow rate where flow transitions to laminar |
| Dynamics | |||
| Nominal condition | |||
| Time | tau1 | 30 | Time constant at nominal flow [s] |
| Time | tau2 | 30 | Time constant at nominal flow [s] |
| Equations | |||
| Dynamics | energyDynamics | Modelica.Fluid.Types.Dynamic... | Type of energy balance: dynamic (3 initialization options) or steady state |
| Dynamics | massDynamics | energyDynamics | Type of mass balance: dynamic (3 initialization options) or steady state |
| Initialization | |||
| Medium 1 | |||
| AbsolutePressure | p1_start | Medium1.p_default | Start value of pressure [Pa] |
| Temperature | T1_start | 273.15 + 25 | Start value of temperature [K] |
| MassFraction | X1_start[Medium1.nX] | Medium1.X_default | Start value of mass fractions m_i/m [kg/kg] |
| ExtraProperty | C1_start[Medium1.nC] | fill(0, Medium1.nC) | Start value of trace substances |
| ExtraProperty | C1_nominal[Medium1.nC] | fill(1E-2, Medium1.nC) | Nominal value of trace substances. (Set to typical order of magnitude.) |
| Medium 2 | |||
| AbsolutePressure | p2_start | Medium2.p_default | Start value of pressure [Pa] |
| Temperature | T2_start | 273.15 + 5 | Start value of temperature [K] |
| MassFraction | X2_start[Medium2.nX] | Medium2.X_default | Start value of mass fractions m_i/m [kg/kg] |
| ExtraProperty | C2_start[Medium2.nC] | fill(0, Medium2.nC) | Start value of trace substances |
| ExtraProperty | C2_nominal[Medium2.nC] | fill(1E-2, Medium2.nC) | Nominal value of trace substances. (Set to typical order of magnitude.) |
Connectors
| Type | Name | Description |
|---|---|---|
| FluidPort_a | port_a1 | Fluid connector a1 (positive design flow direction is from port_a1 to port_b1) |
| FluidPort_b | port_b1 | Fluid connector b1 (positive design flow direction is from port_a1 to port_b1) |
| FluidPort_a | port_a2 | Fluid connector a2 (positive design flow direction is from port_a2 to port_b2) |
| FluidPort_b | port_b2 | Fluid connector b2 (positive design flow direction is from port_a2 to port_b2) |
| input BooleanInput | on | Set to true to enable compressor, or false to disable compressor |
| input RealInput | TSet | Set point for leaving chilled water temperature [K] |
| output RealOutput | P | Electric power consumed by compressor [W] |
