This example tests and demonstrates the implementation of the specific internal
energy versus temperature T(u) relationship for phase-change problems.
Cubic hermite interpolation and linear extrapolation is used to approximate
the piece-wise linear T(u) relationship.
A piece-wise linear T(u) relationship is assumed in all three characteristic regions (solid, mushy and liquid).
The example uses the functions
Buildings.HeatTransfer.Conduction.BaseClasses.der_temperature_u
and
Buildings.HeatTransfer.Conduction.BaseClasses.temeprature_u.
The first function is used to compute
the derivatives at the support points,
and the second function computes the temperature
for a given specific internal energy.
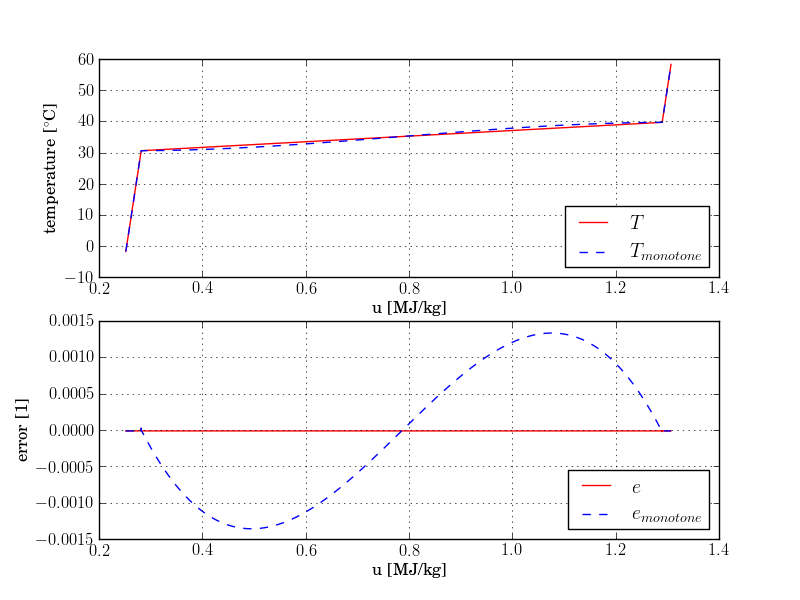
The example also demonstrates the use of cubic hermite spline interpolation with
two different settings: One produces an approximation of the T(u) relationship that is monotone,
whereas the other does not enforce monotonicity.
The latter one is used by default in the Buildings library,
since it produces a higher accuracy in the mushy
region, especially for materials in which phase-change transformation occurs in a wide
temperature interval (see the figure below).
The curves errNonMonotone and
errMonotone
represent the relative error between approximated and exact temperatures
obtained for different specific internal energy values (right hand side figure).
model Temperature_u
"Approximation of specific internal energy versus temperature curve with cubic hermite cubic spline"
extends Modelica.Icons.Example;
// Phase-change properties
parameter Buildings.HeatTransfer.Data.SolidsPCM.Generic
materialMonotone(
TSol=273.15+30.9,
TLiq=273.15+40.0,
LHea=1000000,
c=920,
ensureMonotonicity=true,
d=1000,
k=1,
x=0.2)
"Phase change material with monotone u-T relation";
parameter Buildings.HeatTransfer.Data.SolidsPCM.Generic
materialNonMonotone(TSol=273.15+30.9,
TLiq=273.15+40.0,
LHea=1000000,
c=920,
ensureMonotonicity=false,
d=1000,
k=1,
x=0.2)
"Phase change material with non-monotone u-T relation";
parameter Modelica.SIunits.SpecificInternalEnergy ud[Buildings.HeatTransfer.Conduction.nSupPCM](
each fixed=false)
"Support points";
parameter Modelica.SIunits.SpecificInternalEnergy udMonotone[Buildings.HeatTransfer.Conduction.nSupPCM](
each fixed=false)
"Support points";
parameter Modelica.SIunits.Temperature Td[Buildings.HeatTransfer.Conduction.nSupPCM](
each fixed=false)
"Support points";
parameter Modelica.SIunits.Temperature TdMonotone[Buildings.HeatTransfer.Conduction.nSupPCM](
each fixed=false)
"Support points";
parameter Real dT_du[Buildings.HeatTransfer.Conduction.nSupPCM](
each fixed=false,
each unit="kg.K2/J")
"Derivatives at the support points - non-monotone, default in Modelica PCM";
parameter Real dT_duMonotone[Buildings.HeatTransfer.Conduction.nSupPCM](
each fixed=false,
each unit="kg.K2/J")
"Derivatives at the support points for monotone increasing cubic splines";
Modelica.SIunits.SpecificInternalEnergy u
"Specific internal energy";
Modelica.SIunits.Temperature T
"Temperature for given u without monotone interpolation";
Modelica.SIunits.Temperature TMonotone
"Temperature for given u with monotone interpolation";
Modelica.SIunits.Temperature TExa
"Exact value of temperature";
Real errMonotone
"Relative temperature error between calculated value with monotone interpolation and exact temperature";
Real errNonMonotone
"Relative temperature error between calculated value with non-monotone interpolation and exact temperature";
parameter Modelica.SIunits.TemperatureDifference dTCha = materialMonotone.TSol+materialMonotone.TLiq
"Characteristic temperature difference of the problem";
protected
function relativeError
"Relative error"
input Modelica.SIunits.Temperature T
"Approximated temperature";
input Modelica.SIunits.Temperature TExa
"Exact temperature";
input Modelica.SIunits.TemperatureDifference dTCha
"Characteristic temperature difference";
output Real relErr
"Relative error";
algorithm
relErr :=(T - TExa)/dTCha;
end relativeError;
constant Real conFac(unit="1/s") = 1
"Conversion factor to satisfy unit check";
initial equation
// Calculate derivatives at support points (non-monotone)
(ud, Td, dT_du) =
Buildings.HeatTransfer.Conduction.BaseClasses.der_temperature_u(
c= materialNonMonotone.c,
TSol=materialNonMonotone.TSol,
TLiq=materialNonMonotone.TLiq,
LHea=materialNonMonotone.LHea,
ensureMonotonicity=materialNonMonotone.ensureMonotonicity);
// Calculate derivatives at support points (monotone);
(udMonotone, TdMonotone, dT_duMonotone) =
Buildings.HeatTransfer.Conduction.BaseClasses.der_temperature_u(
c= materialMonotone.c,
TSol=materialMonotone.TSol,
TLiq=materialMonotone.TLiq,
LHea=materialMonotone.LHea,
ensureMonotonicity=materialMonotone.ensureMonotonicity);
equation
u = 2.5e5+time*(1.5*materialMonotone.c*(materialMonotone.TLiq-273.15)+materialMonotone.LHea)*conFac;
// Calculate T based on non-monotone interpolation
T =
Buildings.HeatTransfer.Conduction.BaseClasses.temperature_u(
ud=ud,
Td=Td,
dT_du=dT_du,
u=u);
// Calculate T based on monotone interpolation
TMonotone =
Buildings.HeatTransfer.Conduction.BaseClasses.temperature_u(
ud=udMonotone,
Td=TdMonotone,
dT_du=dT_duMonotone,
u=u);
//Relative errors of obtained temperatures by using monotone and non-monotone
//interpolation against exact values of tempratures taken from the T(u) curve
if time>=1.e-05
then
if u <= materialMonotone.c*materialMonotone.TSol
then
// Solid region
TExa = u/materialMonotone.c;
elseif u >= materialMonotone.c*materialMonotone.TLiq+materialMonotone.LHea
then
// Liquid region
TExa = (u-materialMonotone.LHea)/materialMonotone.c;
else
// Region of phase transition
TExa=((u + materialMonotone.LHea*materialMonotone.TSol/(materialMonotone.TLiq
- materialMonotone.TSol))/(materialMonotone.c + materialMonotone.LHea/(
materialMonotone.TLiq - materialMonotone.TSol)));
end if;
else
TExa =T;
end if;
errNonMonotone =
relativeError(T=T, TExa=TExa, dTCha= dTCha);
errMonotone =
relativeError(T=TMonotone, TExa=TExa, dTCha= dTCha);
end Temperature_u;


 Buildings.HeatTransfer.Conduction.BaseClasses.Examples.Temperature_u
Buildings.HeatTransfer.Conduction.BaseClasses.Examples.Temperature_u