Package with transmission line models for three-phase unbalanced AC systems
Information
This package contains models for transmission lines and electrical networks
of AC three-phase unbalanced systems.
Extends from Modelica.Icons.Package (Icon for standard packages).
Package Content
| Name |
Description |
 Line Line
|
Model of an electrical line without neutral cable |
 Line_N Line_N
|
Model of an electrical line with neutral cable |
 Network Network
|
Three phases unbalanced AC network without neutral cable |
 Network_N Network_N
|
Three phases unbalanced AC network with neutral cable |
 TwoPortInductance TwoPortInductance
|
Model of an inductance with two electrical ports |
 TwoPortInductance_N TwoPortInductance_N
|
Model of an inductance with two electrical ports and neutral line cable |
 TwoPortMatrixRL TwoPortMatrixRL
|
Model of an RL line parameterized with impedance matrices |
 TwoPortMatrixRLC TwoPortMatrixRLC
|
PI model of a line parameterized with impedance and admittance matrices |
 TwoPortMatrixRLC_N TwoPortMatrixRLC_N
|
PI model of a line parameterized with impedance and admittance matrices and neutral line |
 TwoPortMatrixRL_N TwoPortMatrixRL_N
|
Model of an RL line parameterized with impedance matrices and neutral line |
 TwoPortRL TwoPortRL
|
Model of a resistive-inductive element with two electrical ports |
 TwoPortRLC TwoPortRLC
|
Model of an RLC element with two electrical ports |
 TwoPortRLC_N TwoPortRLC_N
|
Model of an RLC element with two electrical ports and neutral line cable |
 TwoPortRL_N TwoPortRL_N
|
Model of a resistive-inductive element with two electrical ports and neutral line cable |
 TwoPortResistance TwoPortResistance
|
Model of a resistance with two electrical ports |
 TwoPortResistance_N TwoPortResistance_N
|
Model of a resistance with two electrical ports and neutral cable |
 Examples Examples
|
Package with example models |
Model of an electrical line without neutral cable
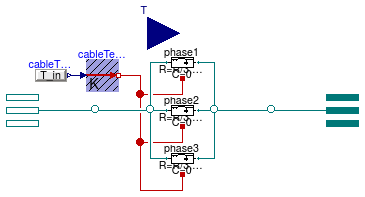
Information
This model represents an AC three-phase unbalanced cable without
neutral connection. The model is based on
Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortRLC
and provides functionalities to parametrize the values of R, L and C
using either commercial cables or default values.
Extends from Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort (Partial model interface for a two port component without neutral cable), Buildings.Electrical.Transmission.BaseClasses.PartialBaseLine (Partial cable line dispersion model).
Parameters
| Type | Name | Default | Description |
|---|
| Length | l | | Length of the line [m] |
| Power | P_nominal | | Nominal power of the line [W] |
| Model |
| Assumptions |
| Boolean | use_C | false | Set to true to add a capacitance in the center of the line |
| Load | modelMode | Buildings.Electrical.Types.L... | Select between steady state and dynamic model |
| Thermal |
| Boolean | use_T | false | If true, enables the input for the temperature of the cable |
| Temperature | TCable | T_ref | Fixed temperature of the cable [K] |
| Tech. specification |
| Auto/Manual mode |
| CableMode | mode | Buildings.Electrical.Types.C... | Select if choosing the cable automatically or between a list of commercial options |
| Manual mode |
| Generic | commercialCable | Buildings.Electrical.Transmi... | Commercial cables options |
Connectors
| Type | Name | Description |
|---|
| Terminal_p | terminal_p | Electric terminal side p |
| Terminal_n | terminal_n | Electric terminal side n |
| input RealInput | T | Temperature of the cable |
Modelica definition
model Line
"Model of an electrical line without neutral cable"
extends Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort;
extends Buildings.Electrical.Transmission.BaseClasses.PartialBaseLine(
V_nominal(start = 480),
commercialCable =
Buildings.Electrical.Transmission.Functions.selectCable_low(P_nominal, V_nominal));
OnePhase.Lines.TwoPortRL phase1(
final useHeatPort=true,
final T_ref=T_ref,
final M=M,
final R=R/3,
final L=L/3,
final mode=modelMode)
"Impedance line 1";
OnePhase.Lines.TwoPortRL phase2(
final useHeatPort=true,
final T_ref=T_ref,
final M=M,
final R=R/3,
final L=L/3,
final mode=modelMode)
"Impedance line 2";
OnePhase.Lines.TwoPortRL phase3(
final useHeatPort=true,
final T_ref=T_ref,
final M=M,
final R=R/3,
final L=L/3,
final mode=modelMode)
"Impedance line 3";
equation
connect(cableTemp.port, phase1.heatPort);
connect(cableTemp.port, phase2.heatPort);
connect(cableTemp.port, phase3.heatPort);
connect(terminal_n.phase[1], phase1.terminal_n);
connect(terminal_n.phase[2], phase2.terminal_n);
connect(terminal_n.phase[3], phase3.terminal_n);
connect(phase1.terminal_p, terminal_p.phase[1]);
connect(phase2.terminal_p, terminal_p.phase[2]);
connect(phase3.terminal_p, terminal_p.phase[3]);
end Line;
Model of an electrical line with neutral cable
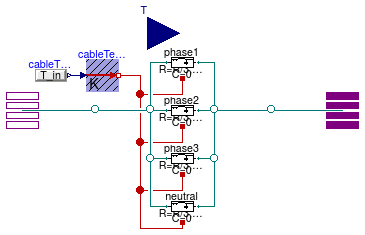
Information
This model represents an AC three-phase unbalanced cable with
neutral connection. The model is based on
Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortRLC
and provides functionalities to parametrize the values of R, L and C
using either commercial cables or default values.
Extends from Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort_N (Partial model interface for a two port component with neutral cable), Buildings.Electrical.Transmission.BaseClasses.PartialBaseLine (Partial cable line dispersion model).
Parameters
| Type | Name | Default | Description |
|---|
| Length | l | | Length of the line [m] |
| Power | P_nominal | | Nominal power of the line [W] |
| Model |
| Assumptions |
| Boolean | use_C | false | Set to true to add a capacitance in the center of the line |
| Load | modelMode | Buildings.Electrical.Types.L... | Select between steady state and dynamic model |
| Thermal |
| Boolean | use_T | false | If true, enables the input for the temperature of the cable |
| Temperature | TCable | T_ref | Fixed temperature of the cable [K] |
| Tech. specification |
| Auto/Manual mode |
| CableMode | mode | Buildings.Electrical.Types.C... | Select if choosing the cable automatically or between a list of commercial options |
| Manual mode |
| Generic | commercialCable | Buildings.Electrical.Transmi... | Commercial cables options |
Connectors
Modelica definition
model Line_N
"Model of an electrical line with neutral cable"
extends Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort_N;
extends Buildings.Electrical.Transmission.BaseClasses.PartialBaseLine(
V_nominal(start = 480),
commercialCable =
Buildings.Electrical.Transmission.Functions.selectCable_low(P_nominal, V_nominal));
OnePhase.Lines.TwoPortRL phase1(
final useHeatPort=true,
final T_ref=T_ref,
final M=M,
final mode=modelMode,
final R=R/3,
final L=L/3)
"Impedance line 1";
OnePhase.Lines.TwoPortRL phase2(
final useHeatPort=true,
final T_ref=T_ref,
final M=M,
final mode=modelMode,
final R=R/3,
final L=L/3)
"Impedance line 1";
OnePhase.Lines.TwoPortRL phase3(
final useHeatPort=true,
final T_ref=T_ref,
final M=M,
final mode=modelMode,
final R=R/3,
final L=L/3)
"Impedance line 1";
OnePhase.Lines.TwoPortRL neutral(
final useHeatPort=true,
final T_ref=T_ref,
final M=M,
final mode=modelMode,
final R=R/3,
final L=L/3)
"Impedance of the neutral cable";
equation
connect(cableTemp.port, phase1.heatPort);
connect(cableTemp.port, phase2.heatPort);
connect(cableTemp.port, phase3.heatPort);
connect(terminal_n.phase[1], phase1.terminal_n);
connect(terminal_n.phase[2], phase2.terminal_n);
connect(terminal_n.phase[3], phase3.terminal_n);
connect(phase1.terminal_p, terminal_p.phase[1]);
connect(phase2.terminal_p, terminal_p.phase[2]);
connect(phase3.terminal_p, terminal_p.phase[3]);
connect(cableTemp.port, neutral.heatPort);
// Neutral cable connection
connect(terminal_n.phase[4], neutral.terminal_n);
connect(terminal_p.phase[4], neutral.terminal_p);
end Line_N;
Three phases unbalanced AC network without neutral cable

Information
This model represents a generalized electrical AC three-phase unbalanced network
without neutral cable.
See
Buildings.Electrical.Transmission.BaseClasses.PartialNetwork
for information about the network model.
See
Buildings.Electrical.Transmission.Grids.PartialGrid
for more information about the topology of the network, such as
the number of nodes, how they are connected, and the length of each connection.
Extends from Transmission.BaseClasses.PartialNetwork (Partial model that represent an electric network).
Parameters
| Type | Name | Default | Description |
|---|
| Voltage | V_nominal | | Nominal voltage of the lines in the network [V] |
Modelica definition
model Network
"Three phases unbalanced AC network without neutral cable"
extends Transmission.BaseClasses.PartialNetwork(
redeclare Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.Terminal_p
terminal,
redeclare replaceable Transmission.Grids.TestGrid2Nodes grid,
redeclare Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.Line lines(commercialCable=grid.cables));
Modelica.SIunits.Voltage VAbs[3,grid.nNodes]
"RMS voltage of the grid nodes";
equation
for i
in 1:grid.nLinks
loop
connect(lines[i].terminal_p, terminal[grid.fromTo[i,1]]);
connect(lines[i].terminal_n, terminal[grid.fromTo[i,2]]);
end for;
for i
in 1:grid.nNodes
loop
VAbs[1,i] =
Buildings.Electrical.PhaseSystems.OnePhase.systemVoltage(terminal[i].phase[1].v);
VAbs[2,i] =
Buildings.Electrical.PhaseSystems.OnePhase.systemVoltage(terminal[i].phase[2].v);
VAbs[3,i] =
Buildings.Electrical.PhaseSystems.OnePhase.systemVoltage(terminal[i].phase[3].v);
end for;
end Network;
Three phases unbalanced AC network with neutral cable

Information
This model represents a generalized electrical AC three-phase unbalanced network
with neutral cable.
See
Buildings.Electrical.Transmission.BaseClasses.PartialNetwork
for information about the network model.
See
Buildings.Electrical.Transmission.Grids.PartialGrid
for more information about the topology of the network, such as
the number of nodes, how they are connected, and the length of each connection.
Extends from Transmission.BaseClasses.PartialNetwork (Partial model that represent an electric network).
Parameters
| Type | Name | Default | Description |
|---|
| Voltage | V_nominal | | Nominal voltage of the lines in the network [V] |
Modelica definition
model Network_N
"Three phases unbalanced AC network with neutral cable"
extends Transmission.BaseClasses.PartialNetwork(
redeclare Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.Terminal4_p
terminal,
redeclare replaceable Transmission.Grids.TestGrid2Nodes grid,
redeclare Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.Line_N lines(
commercialCable=grid.cables));
Modelica.SIunits.Voltage VAbs[3,grid.nNodes]
"RMS voltage of the grid nodes";
equation
for i
in 1:grid.nLinks
loop
connect(lines[i].terminal_p, terminal[grid.fromTo[i,1]]);
connect(lines[i].terminal_n, terminal[grid.fromTo[i,2]]);
end for;
for i
in 1:grid.nNodes
loop
VAbs[1,i] =
Buildings.Electrical.PhaseSystems.OnePhase.systemVoltage(terminal[i].phase[1].v - terminal[i].phase[4].v);
VAbs[2,i] =
Buildings.Electrical.PhaseSystems.OnePhase.systemVoltage(terminal[i].phase[2].v - terminal[i].phase[4].v);
VAbs[3,i] =
Buildings.Electrical.PhaseSystems.OnePhase.systemVoltage(terminal[i].phase[3].v - terminal[i].phase[4].v);
end for;
end Network_N;
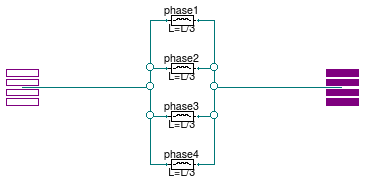
Model of an inductance with two electrical ports
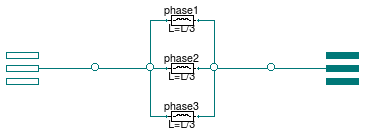
Information
Inductive model that connects two AC three-phase
unbalanced interfaces. This model can be used to represent a
cable in a three-phase unbalanced AC system.
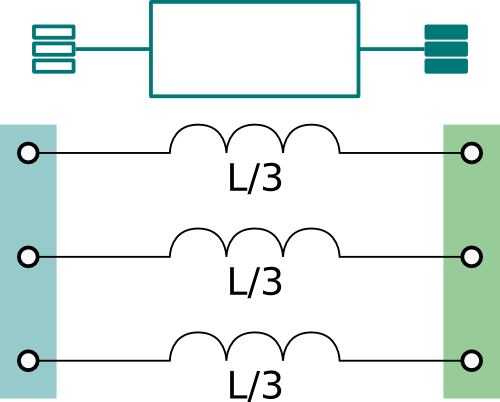
The model represents the lumped inductances as shown in the figure above.
Assuming that the inductance L is the overall inductance of the cable,
each line has an inductance equal to L/3.
Extends from Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort (Partial model interface for a two port component without neutral cable).
Parameters
| Type | Name | Default | Description |
|---|
| Inductance | L | | Inductance [H] |
Connectors
| Type | Name | Description |
|---|
| Terminal_p | terminal_p | Electric terminal side p |
| Terminal_n | terminal_n | Electric terminal side n |
Modelica definition
Model of an inductance with two electrical ports and neutral line cable
Information
Inductive model that connects two AC three-phase
unbalanced interfaces with neutral line. This model can be used to represent a
cable in a three-phase unbalanced AC system.
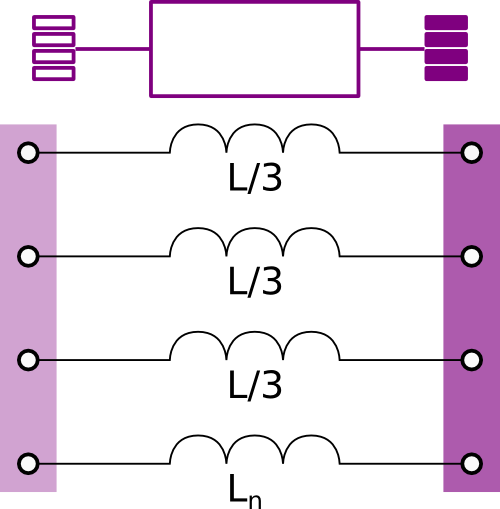
The model represents the lumped inductances as shown in the figure above.
Assuming that the inductance L is the overall inductance of the cable,
each line has an inductance equal to L/3.
The inductance of the neutral cable is defined separately using the parameter
Ln.
Extends from Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort_N (Partial model interface for a two port component with neutral cable).
Parameters
Connectors
| Type | Name | Description |
|---|
| Terminal4_p | terminal_p | Electric terminal side p |
| Terminal4_n | terminal_n | Electric terminal side n |
Modelica definition
Model of an RL line parameterized with impedance matrices

Information
Resistive-inductive model that connects two AC three-phase
unbalanced interfaces. This model can be used to represent a
cable in a three-phase unbalanced AC system.
The voltage between the ports is
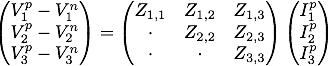
where Vi{p,n} is the voltage phasor at the connector p or
n of the i-th phase, while Iip
the current phasor entering from the connector p of the i-th phase.
The model is parameterized with an impedance matrix Z.
The matrix is symmetric thus just the upper triangular
part of it has to be defined.
Extends from Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort (Partial model interface for a two port component without neutral cable).
Parameters
| Type | Name | Default | Description |
|---|
| Impedance | Z11[2] | | Element [1,1] of impedance matrix [Ohm] |
| Impedance | Z12[2] | | Element [1,2] of impedance matrix [Ohm] |
| Impedance | Z13[2] | | Element [1,3] of impedance matrix [Ohm] |
| Impedance | Z22[2] | | Element [2,2] of impedance matrix [Ohm] |
| Impedance | Z23[2] | | Element [2,3] of impedance matrix [Ohm] |
| Impedance | Z33[2] | | Element [3,3] of impedance matrix [Ohm] |
| Nominal conditions |
| Voltage | V_nominal | | Nominal voltage (V_nominal >= 0) [V] |
Connectors
| Type | Name | Description |
|---|
| Terminal_p | terminal_p | Electric terminal side p |
| Terminal_n | terminal_n | Electric terminal side n |
Modelica definition
model TwoPortMatrixRL
"Model of an RL line parameterized with impedance matrices"
extends Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort;
parameter Modelica.SIunits.Voltage V_nominal(min=0, start=480)
"Nominal voltage (V_nominal >= 0)";
parameter Modelica.SIunits.Impedance Z11[2]
"Element [1,1] of impedance matrix";
parameter Modelica.SIunits.Impedance Z12[2]
"Element [1,2] of impedance matrix";
parameter Modelica.SIunits.Impedance Z13[2]
"Element [1,3] of impedance matrix";
parameter Modelica.SIunits.Impedance Z22[2]
"Element [2,2] of impedance matrix";
parameter Modelica.SIunits.Impedance Z23[2]
"Element [2,3] of impedance matrix";
parameter Modelica.SIunits.Impedance Z33[2]
"Element [3,3] of impedance matrix";
final parameter Modelica.SIunits.Impedance[2] Z21 = Z12
"Element [2,1] of impedance matrix";
final parameter Modelica.SIunits.Impedance[2] Z31 = Z13
"Element [3,1] of impedance matrix";
final parameter Modelica.SIunits.Impedance[2] Z32 = Z23
"Element [3,1] of impedance matrix";
protected
function productAC1p =
Buildings.Electrical.PhaseSystems.OnePhase.product
"Product between complex quantities";
Modelica.SIunits.Current i1[2](
start =
zeros(Buildings.Electrical.PhaseSystems.OnePhase.n),
each stateSelect = StateSelect.prefer) = terminal_n.phase[1].i
"Current in line 1";
Modelica.SIunits.Current i2[2](
start =
zeros(Buildings.Electrical.PhaseSystems.OnePhase.n),
each stateSelect = StateSelect.prefer) = terminal_n.phase[2].i
"Current in line 2";
Modelica.SIunits.Current i3[2](
start =
zeros(Buildings.Electrical.PhaseSystems.OnePhase.n),
each stateSelect = StateSelect.prefer) = terminal_n.phase[3].i
"Current in line 3";
Modelica.SIunits.Voltage v1_n[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= 0),
each stateSelect = StateSelect.never) = terminal_n.phase[1].v
"Voltage in line 1 at connector N";
Modelica.SIunits.Voltage v2_n[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= -2*Modelica.Constants.pi/3),
each stateSelect = StateSelect.never) = terminal_n.phase[2].v
"Voltage in line 2 at connector N";
Modelica.SIunits.Voltage v3_n[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= 2*Modelica.Constants.pi/3),
each stateSelect = StateSelect.never) = terminal_n.phase[3].v
"Voltage in line 3 at connector N";
Modelica.SIunits.Voltage v1_p[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= 0),
each stateSelect = StateSelect.never) = terminal_p.phase[1].v
"Voltage in line 1 at connector P";
Modelica.SIunits.Voltage v2_p[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= -2*Modelica.Constants.pi/3),
each stateSelect = StateSelect.never) = terminal_p.phase[2].v
"Voltage in line 2 at connector P";
Modelica.SIunits.Voltage v3_p[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= 2*Modelica.Constants.pi/3),
each stateSelect = StateSelect.never) = terminal_p.phase[3].v
"Voltage in line 3 at connector P";
equation
// Link the connectors to propagate the overdetermined variable
for i
in 1:3
loop
Connections.branch(terminal_p.phase[i].theta, terminal_n.phase[i].theta);
terminal_p.phase[i].theta = terminal_n.phase[i].theta;
// No current losses, they are preserved in each line
terminal_p.phase[i].i = - terminal_n.phase[i].i;
end for;
// Voltage drop caused by the impedance matrix
v1_n - v1_p =
productAC1p(Z11, i1) +
productAC1p(Z12, i2) +
productAC1p(Z13, i3);
v2_n - v2_p =
productAC1p(Z21, i1) +
productAC1p(Z22, i2) +
productAC1p(Z23, i3);
v3_n - v3_p =
productAC1p(Z31, i1) +
productAC1p(Z32, i2) +
productAC1p(Z33, i3);
end TwoPortMatrixRL;
PI model of a line parameterized with impedance and admittance matrices

Information
RLC line model (π-model) that connects two AC three-phase
unbalanced interfaces. This model can be used to represent a
cable in a three-phase unbalanced AC system.
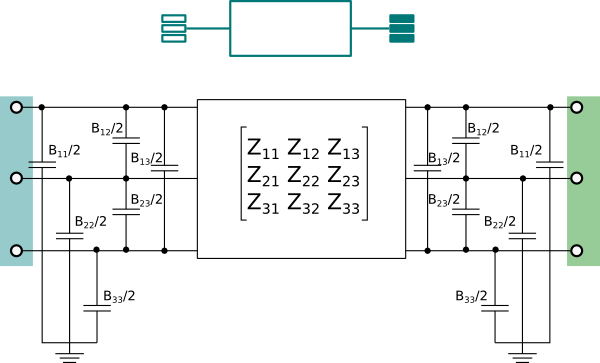
The model is parameterized with an impedance matrix Z and
an admittance matrix B.
The impedance matrix is symmetric, and therefore only the upper triangular
part of the matrix needs to be defined.
This model is a more detailed version of the model
Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortMatrixRL that includes
the capacitive effects of the lines.
Extends from Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort (Partial model interface for a two port component without neutral cable).
Parameters
| Type | Name | Default | Description |
|---|
| Impedance | Z11[2] | | Element [1,1] of impedance matrix [Ohm] |
| Impedance | Z12[2] | | Element [1,2] of impedance matrix [Ohm] |
| Impedance | Z13[2] | | Element [1,3] of impedance matrix [Ohm] |
| Impedance | Z22[2] | | Element [2,2] of impedance matrix [Ohm] |
| Impedance | Z23[2] | | Element [2,3] of impedance matrix [Ohm] |
| Impedance | Z33[2] | | Element [3,3] of impedance matrix [Ohm] |
| Admittance | B11 | | Element [1,1] of admittance matrix [S] |
| Admittance | B12 | | Element [1,2] of admittance matrix [S] |
| Admittance | B13 | | Element [1,3] of admittance matrix [S] |
| Admittance | B22 | | Element [2,2] of admittance matrix [S] |
| Admittance | B23 | | Element [2,3] of admittance matrix [S] |
| Admittance | B33 | | Element [3,3] of admittance matrix [S] |
| Nominal conditions |
| Voltage | V_nominal | | Nominal voltage (V_nominal >= 0) [V] |
Connectors
| Type | Name | Description |
|---|
| Terminal_p | terminal_p | Electric terminal side p |
| Terminal_n | terminal_n | Electric terminal side n |
Modelica definition
model TwoPortMatrixRLC
"PI model of a line parameterized with impedance and admittance matrices"
extends Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort;
parameter Modelica.SIunits.Voltage V_nominal(min=0, start=480)
"Nominal voltage (V_nominal >= 0)";
parameter Modelica.SIunits.Impedance Z11[2]
"Element [1,1] of impedance matrix";
parameter Modelica.SIunits.Impedance Z12[2]
"Element [1,2] of impedance matrix";
parameter Modelica.SIunits.Impedance Z13[2]
"Element [1,3] of impedance matrix";
parameter Modelica.SIunits.Impedance Z22[2]
"Element [2,2] of impedance matrix";
parameter Modelica.SIunits.Impedance Z23[2]
"Element [2,3] of impedance matrix";
parameter Modelica.SIunits.Impedance Z33[2]
"Element [3,3] of impedance matrix";
final parameter Modelica.SIunits.Impedance[2] Z21 = Z12
"Element [2,1] of impedance matrix";
final parameter Modelica.SIunits.Impedance[2] Z31 = Z13
"Element [3,1] of impedance matrix";
final parameter Modelica.SIunits.Impedance[2] Z32 = Z23
"Element [3,1] of impedance matrix";
parameter Modelica.SIunits.Admittance B11
"Element [1,1] of admittance matrix";
parameter Modelica.SIunits.Admittance B12
"Element [1,2] of admittance matrix";
parameter Modelica.SIunits.Admittance B13
"Element [1,3] of admittance matrix";
parameter Modelica.SIunits.Admittance B22
"Element [2,2] of admittance matrix";
parameter Modelica.SIunits.Admittance B23
"Element [2,3] of admittance matrix";
parameter Modelica.SIunits.Admittance B33
"Element [3,3] of admittance matrix";
final parameter Modelica.SIunits.Admittance B21 = B12
"Element [2,1] of admittance matrix";
final parameter Modelica.SIunits.Admittance B31 = B13
"Element [3,1] of admittance matrix";
final parameter Modelica.SIunits.Admittance B32 = B23
"Element [3,2] of admittance matrix";
protected
function productAC1p =
Buildings.Electrical.PhaseSystems.OnePhase.product
"Product between complex quantities";
Modelica.SIunits.Current Isr[3,2](
start =
zeros(3,Buildings.Electrical.PhaseSystems.OnePhase.n),
each stateSelect = StateSelect.prefer)
"Currents that pass through the lines";
Modelica.SIunits.Current Ish_p[3,2](
start =
zeros(3,Buildings.Electrical.PhaseSystems.OnePhase.n),
each stateSelect = StateSelect.prefer)
"Shunt current on side p";
Modelica.SIunits.Current Ish_n[3,2](
start =
zeros(3,Buildings.Electrical.PhaseSystems.OnePhase.n),
each stateSelect = StateSelect.prefer)
"Shunt current on side n";
Modelica.SIunits.Voltage v1_n[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= 0),
each stateSelect = StateSelect.never) = terminal_n.phase[1].v
"Voltage in line 1 at connector N";
Modelica.SIunits.Voltage v2_n[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= -2*Modelica.Constants.pi/3),
each stateSelect = StateSelect.never) = terminal_n.phase[2].v
"Voltage in line 2 at connector N";
Modelica.SIunits.Voltage v3_n[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= 2*Modelica.Constants.pi/3),
each stateSelect = StateSelect.never) = terminal_n.phase[3].v
"Voltage in line 3 at connector N";
Modelica.SIunits.Voltage v1_p[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= 0),
each stateSelect = StateSelect.never) = terminal_p.phase[1].v
"Voltage in line 1 at connector P";
Modelica.SIunits.Voltage v2_p[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= -2*Modelica.Constants.pi/3),
each stateSelect = StateSelect.never) = terminal_p.phase[2].v
"Voltage in line 2 at connector P";
Modelica.SIunits.Voltage v3_p[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= 2*Modelica.Constants.pi/3),
each stateSelect = StateSelect.never) = terminal_p.phase[3].v
"Voltage in line 3 at connector P";
equation
// Link the connectors to propagate the overdetermined variable
for i
in 1:3
loop
Connections.branch(terminal_p.phase[i].theta, terminal_n.phase[i].theta);
terminal_p.phase[i].theta = terminal_n.phase[i].theta;
end for;
// Kirkoff current law for the terminal n (left side)
Isr[1,:] = terminal_n.phase[1].i - Ish_n[1,:];
Isr[2,:] = terminal_n.phase[2].i - Ish_n[2,:];
Isr[3,:] = terminal_n.phase[3].i - Ish_n[3,:];
// Kirkoff current law for the terminal p (right side)
Isr[1,:] + terminal_p.phase[1].i = Ish_p[1,:];
Isr[2,:] + terminal_p.phase[2].i = Ish_p[2,:];
Isr[3,:] + terminal_p.phase[3].i = Ish_p[3,:];
// Voltage drop caused by the impedance matrix
terminal_n.phase[1].v - terminal_p.phase[1].v =
productAC1p(Z11, terminal_n.phase[1].i)
+
productAC1p(Z12, terminal_n.phase[2].i)
+
productAC1p(Z13, terminal_n.phase[3].i);
terminal_n.phase[2].v - terminal_p.phase[2].v =
productAC1p(Z21, terminal_n.phase[1].i)
+
productAC1p(Z22, terminal_n.phase[2].i)
+
productAC1p(Z23, terminal_n.phase[3].i);
terminal_n.phase[3].v - terminal_p.phase[3].v =
productAC1p(Z31, terminal_n.phase[1].i)
+
productAC1p(Z32, terminal_n.phase[2].i)
+
productAC1p(Z33, terminal_n.phase[3].i);
// Current loss at the terminal n
Ish_n[1,:] =
productAC1p({0, B11/2}, v1_n)
+
productAC1p({0, B12/2}, v2_n)
+
productAC1p({0, B13/2}, v3_n);
Ish_n[2,:] =
productAC1p({0, B21/2}, v1_n)
+
productAC1p({0, B22/2}, v2_n)
+
productAC1p({0, B23/2}, v3_n);
Ish_n[3,:] =
productAC1p({0, B31/2}, v1_n)
+
productAC1p({0, B32/2}, v2_n)
+
productAC1p({0, B33/2}, v3_n);
// Current loss at the terminal n
Ish_p[1,:] =
productAC1p({0, B11/2}, v1_p)
+
productAC1p({0, B12/2}, v2_p)
+
productAC1p({0, B13/2}, v3_p);
Ish_p[2,:] =
productAC1p({0, B21/2}, v1_p)
+
productAC1p({0, B22/2}, v2_p)
+
productAC1p({0, B23/2}, v3_p);
Ish_p[3,:] =
productAC1p({0, B31/2}, v1_p)
+
productAC1p({0, B32/2}, v2_p)
+
productAC1p({0, B33/2}, v3_p);
end TwoPortMatrixRLC;
PI model of a line parameterized with impedance and admittance matrices and neutral line

Information
RLC line model (π-model) that connects two AC three-phase
unbalanced interfaces and neutral line. This model can be used to represent a
cable in a three-phase unbalanced AC system.
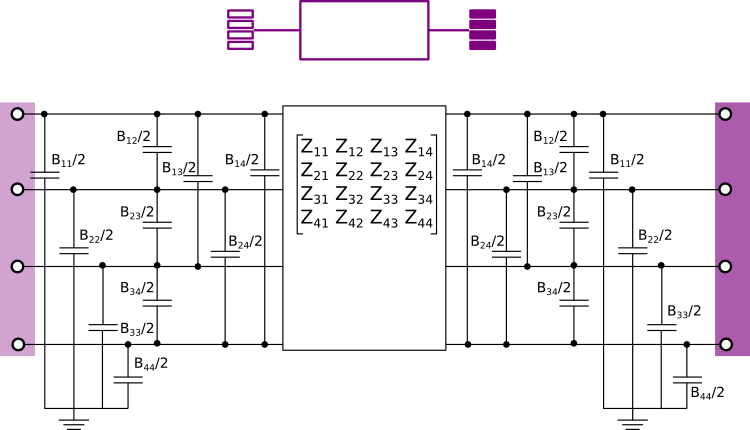
The model is parameterized with an impedance matrix Z and
an admittance matrix B.
The impedance matrix is symmetric, and therefore only the upper triangular
part of the matrix needs to be defined.
This model is a more detailed version of the model
Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortMatrixRL_N that includes
the capacitive effects of the lines.
Note
The fourth line is the neutral one.
Extends from Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort_N (Partial model interface for a two port component with neutral cable).
Parameters
| Type | Name | Default | Description |
|---|
| Impedance | Z11[2] | | Element [1,1] of impedance matrix [Ohm] |
| Impedance | Z12[2] | | Element [1,2] of impedance matrix [Ohm] |
| Impedance | Z13[2] | | Element [1,3] of impedance matrix [Ohm] |
| Impedance | Z14[2] | | Element [1,4] of impedance matrix [Ohm] |
| Impedance | Z22[2] | | Element [2,2] of impedance matrix [Ohm] |
| Impedance | Z23[2] | | Element [2,3] of impedance matrix [Ohm] |
| Impedance | Z24[2] | | Element [2,4] of impedance matrix [Ohm] |
| Impedance | Z33[2] | | Element [3,3] of impedance matrix [Ohm] |
| Impedance | Z34[2] | | Element [3,4] of impedance matrix [Ohm] |
| Impedance | Z44[2] | | Element [4,4] of impedance matrix [Ohm] |
| Admittance | B11 | | Element [1,1] of admittance matrix [S] |
| Admittance | B12 | | Element [1,2] of admittance matrix [S] |
| Admittance | B13 | | Element [1,3] of admittance matrix [S] |
| Admittance | B14 | | Element [1,4] of admittance matrix [S] |
| Admittance | B22 | | Element [2,2] of admittance matrix [S] |
| Admittance | B23 | | Element [2,3] of admittance matrix [S] |
| Admittance | B24 | | Element [2,4] of admittance matrix [S] |
| Admittance | B33 | | Element [3,3] of admittance matrix [S] |
| Admittance | B34 | | Element [3,4] of admittance matrix [S] |
| Admittance | B44 | | Element [4,4] of admittance matrix [S] |
| Nominal conditions |
| Voltage | V_nominal | | Nominal voltage (V_nominal >= 0) [V] |
Connectors
| Type | Name | Description |
|---|
| Terminal4_p | terminal_p | Electric terminal side p |
| Terminal4_n | terminal_n | Electric terminal side n |
Modelica definition
model TwoPortMatrixRLC_N
"PI model of a line parameterized with impedance and admittance matrices and neutral line"
extends Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort_N;
parameter Modelica.SIunits.Voltage V_nominal(min=0, start=480)
"Nominal voltage (V_nominal >= 0)";
parameter Modelica.SIunits.Impedance Z11[2]
"Element [1,1] of impedance matrix";
parameter Modelica.SIunits.Impedance Z12[2]
"Element [1,2] of impedance matrix";
parameter Modelica.SIunits.Impedance Z13[2]
"Element [1,3] of impedance matrix";
parameter Modelica.SIunits.Impedance Z14[2]
"Element [1,4] of impedance matrix";
parameter Modelica.SIunits.Impedance Z22[2]
"Element [2,2] of impedance matrix";
parameter Modelica.SIunits.Impedance Z23[2]
"Element [2,3] of impedance matrix";
parameter Modelica.SIunits.Impedance Z24[2]
"Element [2,4] of impedance matrix";
parameter Modelica.SIunits.Impedance Z33[2]
"Element [3,3] of impedance matrix";
parameter Modelica.SIunits.Impedance Z34[2]
"Element [3,4] of impedance matrix";
parameter Modelica.SIunits.Impedance Z44[2]
"Element [4,4] of impedance matrix";
final parameter Modelica.SIunits.Impedance[2] Z21 = Z12
"Element [2,1] of impedance matrix";
final parameter Modelica.SIunits.Impedance[2] Z31 = Z13
"Element [3,1] of impedance matrix";
final parameter Modelica.SIunits.Impedance[2] Z32 = Z23
"Element [3,1] of impedance matrix";
final parameter Modelica.SIunits.Impedance[2] Z41 = Z14
"Element [4,1] of impedance matrix";
final parameter Modelica.SIunits.Impedance[2] Z42 = Z24
"Element [4,2] of impedance matrix";
final parameter Modelica.SIunits.Impedance[2] Z43 = Z34
"Element [4,3] of impedance matrix";
parameter Modelica.SIunits.Admittance B11
"Element [1,1] of admittance matrix";
parameter Modelica.SIunits.Admittance B12
"Element [1,2] of admittance matrix";
parameter Modelica.SIunits.Admittance B13
"Element [1,3] of admittance matrix";
parameter Modelica.SIunits.Admittance B14
"Element [1,4] of admittance matrix";
parameter Modelica.SIunits.Admittance B22
"Element [2,2] of admittance matrix";
parameter Modelica.SIunits.Admittance B23
"Element [2,3] of admittance matrix";
parameter Modelica.SIunits.Admittance B24
"Element [2,4] of admittance matrix";
parameter Modelica.SIunits.Admittance B33
"Element [3,3] of admittance matrix";
parameter Modelica.SIunits.Admittance B34
"Element [3,4] of admittance matrix";
parameter Modelica.SIunits.Admittance B44
"Element [4,4] of admittance matrix";
final parameter Modelica.SIunits.Admittance B21 = B12
"Element [2,1] of admittance matrix";
final parameter Modelica.SIunits.Admittance B31 = B13
"Element [3,1] of admittance matrix";
final parameter Modelica.SIunits.Admittance B32 = B23
"Element [3,2] of admittance matrix";
final parameter Modelica.SIunits.Admittance B41 = B14
"Element [4,1] of admittance matrix";
final parameter Modelica.SIunits.Admittance B42 = B24
"Element [4,2] of admittance matrix";
final parameter Modelica.SIunits.Admittance B43 = B34
"Element [4,3] of admittance matrix";
protected
function productAC1p =
Buildings.Electrical.PhaseSystems.OnePhase.product
"Product between complex quantities";
Modelica.SIunits.Current Isr[4,2](
start =
zeros(4,Buildings.Electrical.PhaseSystems.OnePhase.n),
each stateSelect = StateSelect.prefer)
"Currents that pass through the lines";
Modelica.SIunits.Current Ish_p[4,2](
start =
zeros(4,Buildings.Electrical.PhaseSystems.OnePhase.n),
each stateSelect = StateSelect.prefer)
"Shunt current on side p";
Modelica.SIunits.Current Ish_n[4,2](
start =
zeros(4,Buildings.Electrical.PhaseSystems.OnePhase.n),
each stateSelect = StateSelect.prefer)
"Shunt current on side n";
Modelica.SIunits.Voltage v1_n[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= 0),
each stateSelect = StateSelect.never) = terminal_n.phase[1].v
"Voltage in line 1 at connector N";
Modelica.SIunits.Voltage v2_n[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= -2*Modelica.Constants.pi/3),
each stateSelect = StateSelect.never) = terminal_n.phase[2].v
"Voltage in line 2 at connector N";
Modelica.SIunits.Voltage v3_n[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= 2*Modelica.Constants.pi/3),
each stateSelect = StateSelect.never) = terminal_n.phase[3].v
"Voltage in line 3 at connector N";
Modelica.SIunits.Voltage v4_n[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(0),
each stateSelect = StateSelect.never) = terminal_n.phase[4].v
"Voltage in line 4 (neutral) at connector N";
Modelica.SIunits.Voltage v1_p[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= 0),
each stateSelect = StateSelect.never) = terminal_p.phase[1].v
"Voltage in line 1 at connector P";
Modelica.SIunits.Voltage v2_p[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= -2*Modelica.Constants.pi/3),
each stateSelect = StateSelect.never) = terminal_p.phase[2].v
"Voltage in line 2 at connector P";
Modelica.SIunits.Voltage v3_p[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= 2*Modelica.Constants.pi/3),
each stateSelect = StateSelect.never) = terminal_p.phase[3].v
"Voltage in line 3 at connector P";
Modelica.SIunits.Voltage v4_p[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(0),
each stateSelect = StateSelect.never) = terminal_p.phase[4].v
"Voltage in line 4 (neutral) at connector P";
equation
// Link the connectors to propagate the overdetermined variable
for i
in 1:4
loop
Connections.branch(terminal_p.phase[i].theta, terminal_n.phase[i].theta);
terminal_p.phase[i].theta = terminal_n.phase[i].theta;
end for;
// Kirkoff current law for the terminal n (left side)
Isr[1,:] = terminal_n.phase[1].i - Ish_n[1,:];
Isr[2,:] = terminal_n.phase[2].i - Ish_n[2,:];
Isr[3,:] = terminal_n.phase[3].i - Ish_n[3,:];
Isr[4,:] = terminal_n.phase[4].i - Ish_n[4,:];
// Kirkoff current law for the terminal p (right side)
Isr[1,:] + terminal_p.phase[1].i = Ish_p[1,:];
Isr[2,:] + terminal_p.phase[2].i = Ish_p[2,:];
Isr[3,:] + terminal_p.phase[3].i = Ish_p[3,:];
Isr[4,:] + terminal_p.phase[4].i = Ish_p[4,:];
// Voltage drop caused by the impedance matrix
terminal_n.phase[1].v - terminal_p.phase[1].v =
productAC1p(Z11, terminal_n.phase[1].i)
+
productAC1p(Z12, terminal_n.phase[2].i)
+
productAC1p(Z13, terminal_n.phase[3].i)
+
productAC1p(Z14, terminal_n.phase[4].i);
terminal_n.phase[2].v - terminal_p.phase[2].v =
productAC1p(Z21, terminal_n.phase[1].i)
+
productAC1p(Z22, terminal_n.phase[2].i)
+
productAC1p(Z23, terminal_n.phase[3].i)
+
productAC1p(Z24, terminal_n.phase[4].i);
terminal_n.phase[3].v - terminal_p.phase[3].v =
productAC1p(Z31, terminal_n.phase[1].i)
+
productAC1p(Z32, terminal_n.phase[2].i)
+
productAC1p(Z33, terminal_n.phase[3].i)
+
productAC1p(Z34, terminal_n.phase[4].i);
terminal_n.phase[4].v - terminal_p.phase[4].v =
productAC1p(Z41, terminal_n.phase[1].i)
+
productAC1p(Z42, terminal_n.phase[2].i)
+
productAC1p(Z43, terminal_n.phase[3].i)
+
productAC1p(Z44, terminal_n.phase[4].i);
// Current loss at the terminal n
Ish_n[1,:] =
productAC1p({0, B11/2}, v1_n)
+
productAC1p({0, B12/2}, v2_n)
+
productAC1p({0, B13/2}, v3_n)
+
productAC1p({0, B14/2}, v4_n);
Ish_n[2,:] =
productAC1p({0, B21/2}, v1_n)
+
productAC1p({0, B22/2}, v2_n)
+
productAC1p({0, B23/2}, v3_n)
+
productAC1p({0, B24/2}, v4_n);
Ish_n[3,:] =
productAC1p({0, B31/2}, v1_n)
+
productAC1p({0, B32/2}, v2_n)
+
productAC1p({0, B33/2}, v3_n)
+
productAC1p({0, B34/2}, v4_n);
Ish_n[4,:] =
productAC1p({0, B41/2}, v1_n)
+
productAC1p({0, B42/2}, v2_n)
+
productAC1p({0, B43/2}, v3_n)
+
productAC1p({0, B44/2}, v4_n);
// Current loss at the terminal n
Ish_p[1,:] =
productAC1p({0, B11/2}, v1_p)
+
productAC1p({0, B12/2}, v2_p)
+
productAC1p({0, B13/2}, v3_p)
+
productAC1p({0, B14/2}, v4_p);
Ish_p[2,:] =
productAC1p({0, B21/2}, v1_p)
+
productAC1p({0, B22/2}, v2_p)
+
productAC1p({0, B23/2}, v3_p)
+
productAC1p({0, B24/2}, v4_p);
Ish_p[3,:] =
productAC1p({0, B31/2}, v1_p)
+
productAC1p({0, B32/2}, v2_p)
+
productAC1p({0, B33/2}, v3_p)
+
productAC1p({0, B34/2}, v4_p);
Ish_p[4,:] =
productAC1p({0, B41/2}, v1_p)
+
productAC1p({0, B42/2}, v2_p)
+
productAC1p({0, B43/2}, v3_p)
+
productAC1p({0, B44/2}, v4_p);
end TwoPortMatrixRLC_N;
Model of an RL line parameterized with impedance matrices and neutral line

Information
Resistive-inductive model that connects two AC three-phase
unbalanced interfaces with neutral line. This model can be used to represent a
cable in a three-phase unbalanced AC system.
The voltage between the ports is
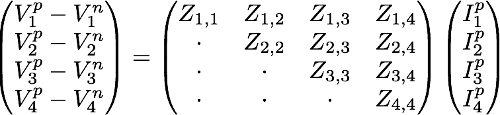
where Vi{p,n} is the voltage phasor at the connector p or
n of the i-th phase, while Iip
the current phasor entering from the connector p of the i-th phase.
The model is parameterized with an impedance matrix Z.
The matrix is symmetric thus just the upper triangular
part of it has to be defined.
Note
The fourth line is the neutral one.
Extends from Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort_N (Partial model interface for a two port component with neutral cable).
Parameters
| Type | Name | Default | Description |
|---|
| Impedance | Z11[2] | | Element [1,1] of impedance matrix [Ohm] |
| Impedance | Z12[2] | | Element [1,2] of impedance matrix [Ohm] |
| Impedance | Z13[2] | | Element [1,3] of impedance matrix [Ohm] |
| Impedance | Z14[2] | | Element [1,4] of impedance matrix [Ohm] |
| Impedance | Z22[2] | | Element [2,2] of impedance matrix [Ohm] |
| Impedance | Z23[2] | | Element [2,3] of impedance matrix [Ohm] |
| Impedance | Z24[2] | | Element [2,4] of impedance matrix [Ohm] |
| Impedance | Z33[2] | | Element [3,3] of impedance matrix [Ohm] |
| Impedance | Z34[2] | | Element [3,4] of impedance matrix [Ohm] |
| Impedance | Z44[2] | | Element [4,4] of impedance matrix [Ohm] |
| Nominal conditions |
| Voltage | V_nominal | | Nominal voltage (V_nominal >= 0) [V] |
Connectors
| Type | Name | Description |
|---|
| Terminal4_p | terminal_p | Electric terminal side p |
| Terminal4_n | terminal_n | Electric terminal side n |
Modelica definition
model TwoPortMatrixRL_N
"Model of an RL line parameterized with impedance matrices and neutral line"
extends Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort_N;
parameter Modelica.SIunits.Voltage V_nominal(min=0, start=480)
"Nominal voltage (V_nominal >= 0)";
parameter Modelica.SIunits.Impedance Z11[2]
"Element [1,1] of impedance matrix";
parameter Modelica.SIunits.Impedance Z12[2]
"Element [1,2] of impedance matrix";
parameter Modelica.SIunits.Impedance Z13[2]
"Element [1,3] of impedance matrix";
parameter Modelica.SIunits.Impedance Z14[2]
"Element [1,4] of impedance matrix";
parameter Modelica.SIunits.Impedance Z22[2]
"Element [2,2] of impedance matrix";
parameter Modelica.SIunits.Impedance Z23[2]
"Element [2,3] of impedance matrix";
parameter Modelica.SIunits.Impedance Z24[2]
"Element [2,4] of impedance matrix";
parameter Modelica.SIunits.Impedance Z33[2]
"Element [3,3] of impedance matrix";
parameter Modelica.SIunits.Impedance Z34[2]
"Element [3,4] of impedance matrix";
parameter Modelica.SIunits.Impedance Z44[2]
"Element [4,4] of impedance matrix";
final parameter Modelica.SIunits.Impedance[2] Z21 = Z12
"Element [2,1] of impedance matrix";
final parameter Modelica.SIunits.Impedance[2] Z31 = Z13
"Element [3,1] of impedance matrix";
final parameter Modelica.SIunits.Impedance[2] Z32 = Z23
"Element [3,1] of impedance matrix";
final parameter Modelica.SIunits.Impedance[2] Z41 = Z14
"Element [4,1] of impedance matrix";
final parameter Modelica.SIunits.Impedance[2] Z42 = Z24
"Element [4,2] of impedance matrix";
final parameter Modelica.SIunits.Impedance[2] Z43 = Z34
"Element [4,3] of impedance matrix";
protected
function productAC1p =
Buildings.Electrical.PhaseSystems.OnePhase.product
"Product between complex quantities";
Modelica.SIunits.Current i1[2](
start =
zeros(Buildings.Electrical.PhaseSystems.OnePhase.n),
each stateSelect = StateSelect.prefer) = terminal_n.phase[1].i
"Current in line 1";
Modelica.SIunits.Current i2[2](
start =
zeros(Buildings.Electrical.PhaseSystems.OnePhase.n),
each stateSelect = StateSelect.prefer) = terminal_n.phase[2].i
"Current in line 2";
Modelica.SIunits.Current i3[2](
start =
zeros(Buildings.Electrical.PhaseSystems.OnePhase.n),
each stateSelect = StateSelect.prefer) = terminal_n.phase[3].i
"Current in line 3";
Modelica.SIunits.Current i4[2](
start =
zeros(Buildings.Electrical.PhaseSystems.OnePhase.n),
each stateSelect = StateSelect.prefer) = terminal_n.phase[4].i
"Current in line 4 (neutral)";
Modelica.SIunits.Voltage v1_n[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= 0),
each stateSelect = StateSelect.never) = terminal_n.phase[1].v
"Voltage in line 1 at connector N";
Modelica.SIunits.Voltage v2_n[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= -2*Modelica.Constants.pi/3),
each stateSelect = StateSelect.never) = terminal_n.phase[2].v
"Voltage in line 2 at connector N";
Modelica.SIunits.Voltage v3_n[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= 2*Modelica.Constants.pi/3),
each stateSelect = StateSelect.never) = terminal_n.phase[3].v
"Voltage in line 3 at connector N";
Modelica.SIunits.Voltage v4_n[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(0),
each stateSelect = StateSelect.never) = terminal_n.phase[4].v
"Voltage in line 4 (neutral) at connector N";
Modelica.SIunits.Voltage v1_p[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= 0),
each stateSelect = StateSelect.never) = terminal_p.phase[1].v
"Voltage in line 1 at connector P";
Modelica.SIunits.Voltage v2_p[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= -2*Modelica.Constants.pi/3),
each stateSelect = StateSelect.never) = terminal_p.phase[2].v
"Voltage in line 2 at connector P";
Modelica.SIunits.Voltage v3_p[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(V_nominal/
sqrt(3), phi= 2*Modelica.Constants.pi/3),
each stateSelect = StateSelect.never) = terminal_p.phase[3].v
"Voltage in line 3 at connector P";
Modelica.SIunits.Voltage v4_p[2](
start =
Buildings.Electrical.PhaseSystems.OnePhase.phaseVoltages(0),
each stateSelect = StateSelect.never) = terminal_p.phase[4].v
"Voltage in line 4 (neutral) at connector P";
equation
// Link the connectors to propagate the overdetermined variable
for i
in 1:4
loop
Connections.branch(terminal_p.phase[i].theta, terminal_n.phase[i].theta);
terminal_p.phase[i].theta = terminal_n.phase[i].theta;
// No current losses, they are preserved in each line
terminal_p.phase[i].i = - terminal_n.phase[i].i;
end for;
// Voltage drop caused by the impedance matrix
v1_n - v1_p =
productAC1p(Z11, i1) +
productAC1p(Z12, i2) +
productAC1p(Z13, i3)+
productAC1p(Z14, i4);
v2_n - v2_p =
productAC1p(Z21, i1) +
productAC1p(Z22, i2) +
productAC1p(Z23, i3)+
productAC1p(Z24, i4);
v3_n - v3_p =
productAC1p(Z31, i1) +
productAC1p(Z32, i2) +
productAC1p(Z33, i3)+
productAC1p(Z34, i4);
v4_n - v4_p =
productAC1p(Z41, i1) +
productAC1p(Z42, i2) +
productAC1p(Z43, i3)+
productAC1p(Z44, i4);
end TwoPortMatrixRL_N;
Model of a resistive-inductive element with two electrical ports
Information
Resistive-inductive model that connects two AC three-phase
unbalanced interfaces. This model can be used to represent a
cable in a three-phase unbalanced AC system.
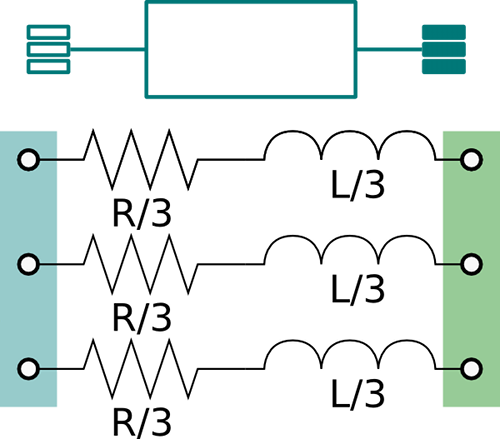
The model represents the lumped impedances as shown in the figure above.
Assuming that the overall cable has a resistance R and an inductance
L, each line has an inductance equal to L/3 and a resistance
equal to R/3.
Extends from Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network), Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort (Partial model interface for a two port component without neutral cable).
Parameters
| Type | Name | Default | Description |
|---|
| Boolean | useHeatPort | false | =true, if HeatPort is enabled |
| Temperature | T | 293.15 | Fixed device temperature if useHeatPort = false [K] |
| Resistance | R | | Resistance at temperature T_ref [Ohm] |
| Temperature | T_ref | 298.15 | Reference temperature [K] |
| Temperature | M | 507.65 | Temperature constant (R_actual = R*(M + T_heatPort)/(M + T_ref)) [K] |
| Inductance | L | | Inductance [H] |
| Current | i1_start[2] | {0,0} | Initial current phasor of phase 1 (positive if entering from terminal p) [A] |
| Current | i2_start[2] | {0,0} | Initial current phasor of phase 2 (positive if entering from terminal p) [A] |
| Current | i3_start[2] | {0,0} | Initial current phasor of phase 3 (positive if entering from terminal p) [A] |
| Modelling assumption |
| Load | mode | Buildings.Electrical.Types.L... | Type of model (e.g., steady state, dynamic, prescribed power consumption, etc.) |
Connectors
Modelica definition
model TwoPortRL
"Model of a resistive-inductive element with two electrical ports"
extends Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort;
extends Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort;
parameter Modelica.SIunits.Resistance R
"Resistance at temperature T_ref";
parameter Modelica.SIunits.Temperature T_ref = 298.15
"Reference temperature";
parameter Modelica.SIunits.Temperature M = 507.65
"Temperature constant (R_actual = R*(M + T_heatPort)/(M + T_ref))";
parameter Modelica.SIunits.Inductance L
"Inductance";
parameter Modelica.SIunits.Current i1_start[2] = {0,0}
"Initial current phasor of phase 1 (positive if entering from terminal p)";
parameter Modelica.SIunits.Current i2_start[2] = {0,0}
"Initial current phasor of phase 2 (positive if entering from terminal p)";
parameter Modelica.SIunits.Current i3_start[2] = {0,0}
"Initial current phasor of phase 3 (positive if entering from terminal p)";
parameter Buildings.Electrical.Types.Load mode(
min=Buildings.Electrical.Types.Load.FixedZ_steady_state,
max=Buildings.Electrical.Types.Load.FixedZ_dynamic) = Buildings.Electrical.Types.Load.FixedZ_steady_state
"Type of model (e.g., steady state, dynamic, prescribed power consumption, etc.)";
OnePhase.Lines.TwoPortRL phase1(
final T_ref=T_ref,
final M=M,
final R=R/3,
final L=L/3,
final mode=mode,
final useHeatPort=useHeatPort,
i_start=i1_start)
"Impedance line 1";
OnePhase.Lines.TwoPortRL phase2(
final T_ref=T_ref,
final M=M,
final R=R/3,
final L=L/3,
final mode=mode,
final useHeatPort=useHeatPort,
i_start=i2_start)
"Impedance line 2";
OnePhase.Lines.TwoPortRL phase3(
final T_ref=T_ref,
final M=M,
final R=R/3,
final L=L/3,
final mode=mode,
final useHeatPort=useHeatPort,
i_start=i3_start)
"Impedance line 3";
equation
// Joule Losses
LossPower = phase1.LossPower + phase2.LossPower + phase3.LossPower;
connect(terminal_n.phase[1], phase1.terminal_n);
connect(terminal_n.phase[2], phase2.terminal_n);
connect(terminal_n.phase[3], phase3.terminal_n);
connect(phase1.terminal_p, terminal_p.phase[1]);
connect(phase2.terminal_p, terminal_p.phase[2]);
connect(phase3.terminal_p, terminal_p.phase[3]);
connect(phase1.heatPort, heatPort);
connect(phase3.heatPort, heatPort);
connect(phase2.heatPort, heatPort);
end TwoPortRL;
Model of an RLC element with two electrical ports
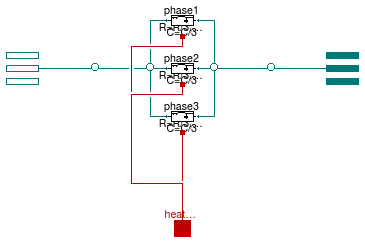
Information
RLC line model (T-model) that connects two AC three-phase
unbalanced interfaces. This model can be used to represent a
cable in a three-phase unbalanced AC system.
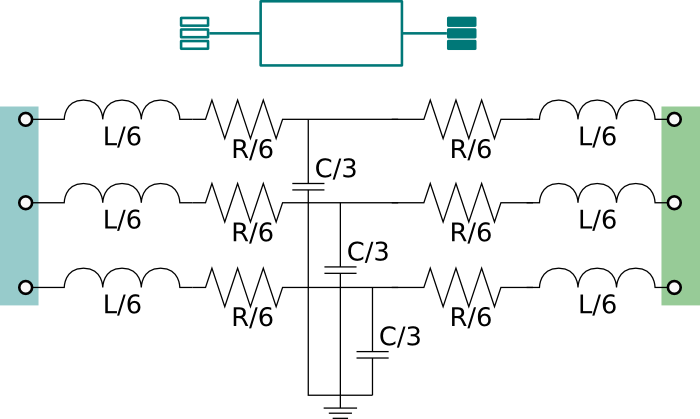
The model represents the lumped impedances as shown in the figure above.
Assuming that the overall cable has a resistance R, an inductance
L, and a capacitance C, each line has an inductance equal
to L/3, a resistance equal to R/3 and a capacity equal to
C/3.
Extends from Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network), Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort (Partial model interface for a two port component without neutral cable).
Parameters
| Type | Name | Default | Description |
|---|
| Boolean | useHeatPort | false | =true, if HeatPort is enabled |
| Temperature | T | 293.15 | Fixed device temperature if useHeatPort = false [K] |
| Resistance | R | | Resistance at temperature T_ref [Ohm] |
| Capacitance | C | | Capacity [F] |
| Inductance | L | | Inductance [H] |
| Temperature | T_ref | 298.15 | Reference temperature [K] |
| Temperature | M | 507.65 | Temperature constant (R_actual = R*(M + T_heatPort)/(M + T_ref)) [K] |
| Voltage | Vc1_start[2] | V_nominal/sqrt(3)*{1,0} | Initial voltage phasor of the capacitance located in the middle of phase 1 [V] |
| Voltage | Vc2_start[2] | V_nominal/sqrt(3)*{-1/2,-sqr... | Initial voltage phasor of the capacitance located in the middle of phase 1 [V] |
| Voltage | Vc3_start[2] | V_nominal/sqrt(3)*{-1/2,+sqr... | Initial voltage phasor of the capacitance located in the middle of phase 1 [V] |
| Modelling assumption |
| Load | mode | Buildings.Electrical.Types.L... | Type of model (e.g., steady state, dynamic, prescribed power consumption, etc.) |
| Nominal conditions |
| Voltage | V_nominal | | Nominal voltage (V_nominal >= 0) [V] |
Connectors
Modelica definition
model TwoPortRLC
"Model of an RLC element with two electrical ports"
extends Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort;
extends Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort;
parameter Modelica.SIunits.Resistance R
"Resistance at temperature T_ref";
parameter Modelica.SIunits.Capacitance C
"Capacity";
parameter Modelica.SIunits.Inductance L
"Inductance";
parameter Modelica.SIunits.Temperature T_ref = 298.15
"Reference temperature";
parameter Modelica.SIunits.Temperature M = 507.65
"Temperature constant (R_actual = R*(M + T_heatPort)/(M + T_ref))";
parameter Modelica.SIunits.Voltage Vc1_start[2] = V_nominal/
sqrt(3)*{1,0}
"Initial voltage phasor of the capacitance located in the middle of phase 1";
parameter Modelica.SIunits.Voltage Vc2_start[2] = V_nominal/
sqrt(3)*{-1/2,-
sqrt(3)/2}
"Initial voltage phasor of the capacitance located in the middle of phase 1";
parameter Modelica.SIunits.Voltage Vc3_start[2] = V_nominal/
sqrt(3)*{-1/2,+
sqrt(3)/2}
"Initial voltage phasor of the capacitance located in the middle of phase 1";
parameter Buildings.Electrical.Types.Load mode(
min=Buildings.Electrical.Types.Load.FixedZ_steady_state,
max=Buildings.Electrical.Types.Load.FixedZ_dynamic)=
Buildings.Electrical.Types.Load.FixedZ_steady_state
"Type of model (e.g., steady state, dynamic, prescribed power consumption, etc.)";
parameter Modelica.SIunits.Voltage V_nominal(min=0, start=480)
"Nominal voltage (V_nominal >= 0)";
OnePhase.Lines.TwoPortRLC phase1(
final T_ref=T_ref,
final M=M,
final R=R/3,
final L=L/3,
final C=C/3,
final mode=mode,
final V_nominal = V_nominal/
sqrt(3),
final useHeatPort=useHeatPort,
Vc_start=Vc1_start)
"Impedance line 1";
OnePhase.Lines.TwoPortRLC phase2(
final T_ref=T_ref,
final M=M,
final R=R/3,
final L=L/3,
final C=C/3,
final mode=mode,
final V_nominal = V_nominal/
sqrt(3),
final useHeatPort=useHeatPort,
Vc_start=Vc2_start)
"Impedance line 2";
OnePhase.Lines.TwoPortRLC phase3(
final T_ref=T_ref,
final M=M,
final R=R/3,
final L=L/3,
final C=C/3,
final mode=mode,
final V_nominal = V_nominal/
sqrt(3),
final useHeatPort=useHeatPort,
Vc_start=Vc3_start)
"Impedance line 3";
equation
// Joule Losses
LossPower = phase1.LossPower + phase2.LossPower + phase3.LossPower;
connect(terminal_n.phase[1], phase1.terminal_n);
connect(terminal_n.phase[2], phase2.terminal_n);
connect(terminal_n.phase[3], phase3.terminal_n);
connect(phase1.terminal_p, terminal_p.phase[1]);
connect(phase2.terminal_p, terminal_p.phase[2]);
connect(phase3.terminal_p, terminal_p.phase[3]);
connect(phase1.heatPort, heatPort);
connect(phase3.heatPort, heatPort);
connect(phase2.heatPort, heatPort);
end TwoPortRLC;
Model of an RLC element with two electrical ports and neutral line cable
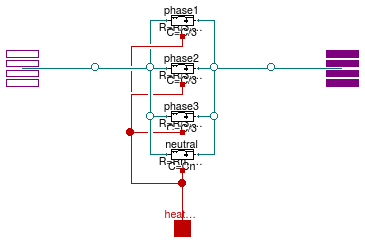
Information
RLC line model (T-model) that connects two AC three-phase
unbalanced interfaces with neutral line. This model can be used to represent a
cable in a three-phase unbalanced AC system.
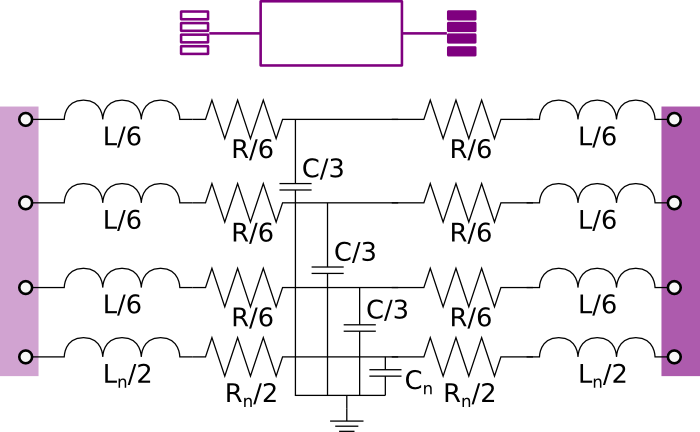
The model represents the lumped impedances as shown in the figure above.
Assuming that the overall cable has a resistance R, an inductance
L, and a capacitance C, each line has an inductance equal
to L/3, a resistance equal to R/3 and a capacity equal to
C/3.
The resistance, capacitance and inductance of the neutral cable are defined separately using the parameters
Rn Cn, and Ln.
Extends from Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network), Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort_N (Partial model interface for a two port component with neutral cable).
Parameters
| Type | Name | Default | Description |
|---|
| Boolean | useHeatPort | false | =true, if HeatPort is enabled |
| Temperature | T | 293.15 | Fixed device temperature if useHeatPort = false [K] |
| Resistance | R | | Resistance at temperature T_ref [Ohm] |
| Resistance | Rn | | Resistance of neutral cable at temperature T_ref [Ohm] |
| Capacitance | C | | Capacity [F] |
| Capacitance | Cn | | Capacityof neutral cable [F] |
| Inductance | L | | Inductance [H] |
| Inductance | Ln | | Inductance of neutral cable [H] |
| Temperature | T_ref | 298.15 | Reference temperature [K] |
| Temperature | M | 507.65 | Temperature constant (R_actual = R*(M + T_heatPort)/(M + T_ref)) [K] |
| Voltage | Vc1_start[2] | V_nominal/sqrt(3)*{1,0} | Initial voltage phasor of the capacitance located in the middle of phase 1 [V] |
| Voltage | Vc2_start[2] | V_nominal/sqrt(3)*{-1/2,-sqr... | Initial voltage phasor of the capacitance located in the middle of phase 1 [V] |
| Voltage | Vc3_start[2] | V_nominal/sqrt(3)*{-1/2,+sqr... | Initial voltage phasor of the capacitance located in the middle of phase 1 [V] |
| Modelling assumption |
| Load | mode | Buildings.Electrical.Types.L... | Type of model (e.g., steady state, dynamic, prescribed power consumption, etc.) |
| Nominal conditions |
| Voltage | V_nominal | | Nominal voltage (V_nominal >= 0) [V] |
Connectors
Modelica definition
model TwoPortRLC_N
"Model of an RLC element with two electrical ports and neutral line cable"
extends Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort;
extends Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort_N;
parameter Modelica.SIunits.Resistance R
"Resistance at temperature T_ref";
parameter Modelica.SIunits.Resistance Rn
"Resistance of neutral cable at temperature T_ref";
parameter Modelica.SIunits.Capacitance C
"Capacity";
parameter Modelica.SIunits.Capacitance Cn
"Capacityof neutral cable";
parameter Modelica.SIunits.Inductance L
"Inductance";
parameter Modelica.SIunits.Inductance Ln
"Inductance of neutral cable";
parameter Modelica.SIunits.Temperature T_ref = 298.15
"Reference temperature";
parameter Modelica.SIunits.Temperature M = 507.65
"Temperature constant (R_actual = R*(M + T_heatPort)/(M + T_ref))";
parameter Modelica.SIunits.Voltage Vc1_start[2] = V_nominal/
sqrt(3)*{1,0}
"Initial voltage phasor of the capacitance located in the middle of phase 1";
parameter Modelica.SIunits.Voltage Vc2_start[2] = V_nominal/
sqrt(3)*{-1/2,-
sqrt(3)/2}
"Initial voltage phasor of the capacitance located in the middle of phase 1";
parameter Modelica.SIunits.Voltage Vc3_start[2] = V_nominal/
sqrt(3)*{-1/2,+
sqrt(3)/2}
"Initial voltage phasor of the capacitance located in the middle of phase 1";
parameter Buildings.Electrical.Types.Load mode(
min=Buildings.Electrical.Types.Load.FixedZ_steady_state,
max=Buildings.Electrical.Types.Load.FixedZ_dynamic)=
Buildings.Electrical.Types.Load.FixedZ_steady_state
"Type of model (e.g., steady state, dynamic, prescribed power consumption, etc.)";
parameter Modelica.SIunits.Voltage V_nominal(min=0, start=480)
"Nominal voltage (V_nominal >= 0)";
OnePhase.Lines.TwoPortRLC phase1(
final T_ref=T_ref,
final M=M,
final R=R/3,
final L=L/3,
final C=C/3,
final mode=mode,
final V_nominal = V_nominal/
sqrt(3),
final useHeatPort=useHeatPort,
Vc_start=Vc1_start)
"Impedance line 1";
OnePhase.Lines.TwoPortRLC phase2(
final T_ref=T_ref,
final M=M,
final R=R/3,
final L=L/3,
final C=C/3,
final mode=mode,
final V_nominal = V_nominal/
sqrt(3),
final useHeatPort=useHeatPort,
Vc_start=Vc2_start)
"Impedance line 2";
OnePhase.Lines.TwoPortRLC phase3(
final T_ref=T_ref,
final M=M,
final R=R/3,
final L=L/3,
final C=C/3,
final mode=mode,
final V_nominal = V_nominal/
sqrt(3),
final useHeatPort=useHeatPort,
Vc_start=Vc3_start)
"Impedance line 3";
OnePhase.Lines.TwoPortRLC neutral(
final T_ref=T_ref,
final M=M,
final mode=mode,
final V_nominal=V_nominal/
sqrt(3),
final useHeatPort=useHeatPort,
final R=Rn,
final C=Cn,
final L=Ln,
Vc_start=-Vc1_start - Vc2_start - Vc3_start)
"Neutral line RLC model";
equation
// Joule Losses
LossPower = phase1.LossPower + phase2.LossPower + phase3.LossPower + neutral.LossPower;
connect(terminal_n.phase[1], phase1.terminal_n);
connect(terminal_n.phase[2], phase2.terminal_n);
connect(terminal_n.phase[3], phase3.terminal_n);
connect(phase1.terminal_p, terminal_p.phase[1]);
connect(phase2.terminal_p, terminal_p.phase[2]);
connect(phase3.terminal_p, terminal_p.phase[3]);
connect(phase1.heatPort, heatPort);
connect(phase3.heatPort, heatPort);
connect(phase2.heatPort, heatPort);
connect(neutral.terminal_p, terminal_p.phase[4]);
connect(neutral.terminal_n, terminal_n.phase[4]);
connect(neutral.heatPort, heatPort);
end TwoPortRLC_N;
Model of a resistive-inductive element with two electrical ports and neutral line cable
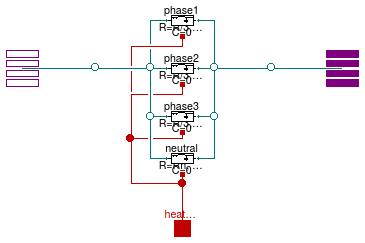
Information
Resistive-inductive model that connects two AC three-phase
unbalanced interfaces with neutral line. This model can be used to represent a
cable in a three-phase unbalanced AC system.
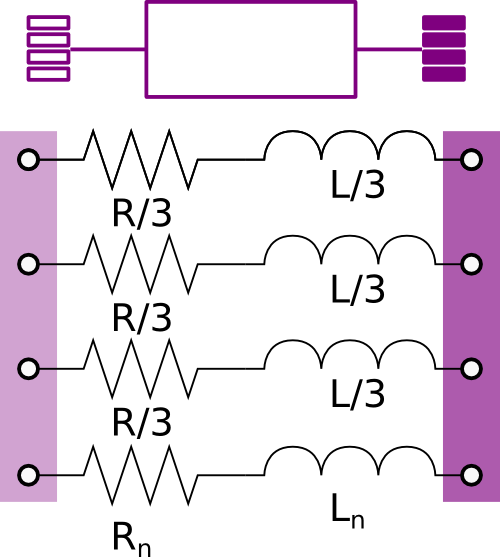
The model represents the lumped impedances as shown in the figure above.
Assuming that the overall cable has a resistance R and an inductance
L, each line has an inductance equal to L/3 and a resistance
equal to R/3.
The resistance and the inductance of the neutral cable are defined separately using the parameters
Rn and Ln.
Extends from Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network), Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort_N (Partial model interface for a two port component with neutral cable).
Parameters
| Type | Name | Default | Description |
|---|
| Boolean | useHeatPort | false | =true, if HeatPort is enabled |
| Temperature | T | 293.15 | Fixed device temperature if useHeatPort = false [K] |
| Resistance | R | | Resistance at temperature T_ref [Ohm] |
| Resistance | Rn | | Resistance of neutral cable at temperature T_ref [Ohm] |
| Temperature | T_ref | 298.15 | Reference temperature [K] |
| Temperature | M | 507.65 | Temperature constant (R_actual = R*(M + T_heatPort)/(M + T_ref)) [K] |
| Inductance | L | | Inductance [H] |
| Inductance | Ln | | Inductance of neutral cable [H] |
| Current | i1_start[2] | {0,0} | Initial current phasor of phase 1 (positive if entering from terminal p) [A] |
| Current | i2_start[2] | {0,0} | Initial current phasor of phase 2 (positive if entering from terminal p) [A] |
| Current | i3_start[2] | {0,0} | Initial current phasor of phase 3 (positive if entering from terminal p) [A] |
| Modelling assumption |
| Load | mode | Buildings.Electrical.Types.L... | Type of model (e.g., steady state, dynamic, prescribed power consumption, etc.) |
Connectors
Modelica definition
model TwoPortRL_N
"Model of a resistive-inductive element with two electrical ports and neutral line cable"
extends Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort;
extends Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort_N;
parameter Modelica.SIunits.Resistance R
"Resistance at temperature T_ref";
parameter Modelica.SIunits.Resistance Rn
"Resistance of neutral cable at temperature T_ref";
parameter Modelica.SIunits.Temperature T_ref = 298.15
"Reference temperature";
parameter Modelica.SIunits.Temperature M = 507.65
"Temperature constant (R_actual = R*(M + T_heatPort)/(M + T_ref))";
parameter Modelica.SIunits.Inductance L
"Inductance";
parameter Modelica.SIunits.Inductance Ln
"Inductance of neutral cable";
parameter Modelica.SIunits.Current i1_start[2] = {0,0}
"Initial current phasor of phase 1 (positive if entering from terminal p)";
parameter Modelica.SIunits.Current i2_start[2] = {0,0}
"Initial current phasor of phase 2 (positive if entering from terminal p)";
parameter Modelica.SIunits.Current i3_start[2] = {0,0}
"Initial current phasor of phase 3 (positive if entering from terminal p)";
parameter Buildings.Electrical.Types.Load mode(
min=Buildings.Electrical.Types.Load.FixedZ_steady_state,
max=Buildings.Electrical.Types.Load.FixedZ_dynamic) = Buildings.Electrical.Types.Load.FixedZ_steady_state
"Type of model (e.g., steady state, dynamic, prescribed power consumption, etc.)";
OnePhase.Lines.TwoPortRL phase1(
final T_ref=T_ref,
final M=M,
final R=R/3,
final L=L/3,
final mode=mode,
final useHeatPort=useHeatPort,
i_start=i1_start)
"Impedance line 1";
OnePhase.Lines.TwoPortRL phase2(
final T_ref=T_ref,
final M=M,
final R=R/3,
final L=L/3,
final mode=mode,
final useHeatPort=useHeatPort,
i_start=i2_start)
"Impedance line 2";
OnePhase.Lines.TwoPortRL phase3(
final T_ref=T_ref,
final M=M,
final R=R/3,
final L=L/3,
final mode=mode,
final useHeatPort=useHeatPort,
i_start=i3_start)
"Impedance line 3";
OnePhase.Lines.TwoPortRL neutral(
final T_ref=T_ref,
final M=M,
final mode=mode,
final useHeatPort=useHeatPort,
final R=Rn,
final L=Ln,
i_start=-i1_start - i2_start - i3_start)
"neutral cable RL model";
equation
// Joule Losses
LossPower = phase1.LossPower + phase2.LossPower + phase3.LossPower + neutral.LossPower;
connect(terminal_n.phase[1], phase1.terminal_n);
connect(terminal_n.phase[2], phase2.terminal_n);
connect(terminal_n.phase[3], phase3.terminal_n);
connect(phase1.terminal_p, terminal_p.phase[1]);
connect(phase2.terminal_p, terminal_p.phase[2]);
connect(phase3.terminal_p, terminal_p.phase[3]);
connect(phase1.heatPort, heatPort);
connect(phase3.heatPort, heatPort);
connect(phase2.heatPort, heatPort);
connect(neutral.heatPort, heatPort);
connect(neutral.terminal_p, terminal_p.phase[4]);
connect(neutral.terminal_n, terminal_n.phase[4]);
end TwoPortRL_N;
Model of a resistance with two electrical ports
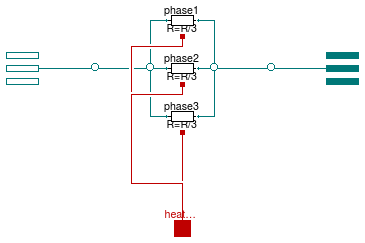
Information
Resistive model that connects two AC three-phase
unbalanced interfaces. This model can be used to represent a
cable in a three-phase unbalanced AC system.
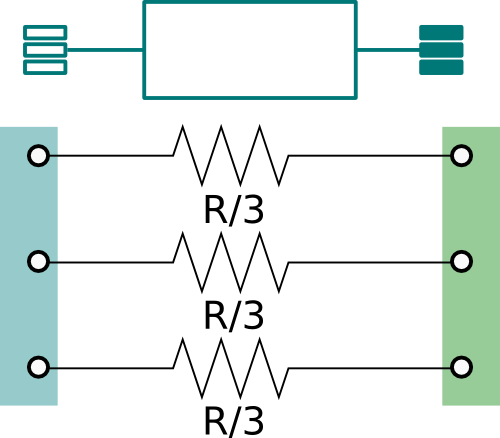
The model represents the lumped resistance as shown in the figure above.
Assuming that the resistance R is the overall resistance of the cable,
each line has a resistance equal to R/3.
Extends from Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network), Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort (Partial model interface for a two port component without neutral cable).
Parameters
| Type | Name | Default | Description |
|---|
| Boolean | useHeatPort | false | =true, if HeatPort is enabled |
| Temperature | T | 293.15 | Fixed device temperature if useHeatPort = false [K] |
| Temperature | T_ref | 298.15 | Reference temperature [K] |
| Temperature | M | 507.65 | Temperature constant (R_actual = R*(M + T_heatPort)/(M + T_ref)) [K] |
| Resistance | R | | Resistance at temperature T_ref [Ohm] |
Connectors
Modelica definition
model TwoPortResistance
"Model of a resistance with two electrical ports"
extends Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort;
extends Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort;
parameter Modelica.SIunits.Temperature T_ref = 298.15
"Reference temperature";
parameter Modelica.SIunits.Temperature M = 507.65
"Temperature constant (R_actual = R*(M + T_heatPort)/(M + T_ref))";
parameter Modelica.SIunits.Resistance R
"Resistance at temperature T_ref";
OnePhase.Lines.TwoPortResistance phase1(
final T_ref=T_ref,
final M=M,
final R=R/3,
final useHeatPort=useHeatPort)
"Resistance line 1";
OnePhase.Lines.TwoPortResistance phase2(
final T_ref=T_ref,
final M=M,
final R=R/3,
final useHeatPort=useHeatPort)
"Resistance line 2";
OnePhase.Lines.TwoPortResistance phase3(
final T_ref=T_ref,
final M=M,
final R=R/3,
final useHeatPort=useHeatPort)
"Resistance line 3";
equation
// Joule Losses
LossPower = phase1.LossPower + phase2.LossPower + phase3.LossPower;
connect(terminal_n.phase[1], phase1.terminal_n);
connect(terminal_n.phase[2], phase2.terminal_n);
connect(terminal_n.phase[3], phase3.terminal_n);
connect(phase1.terminal_p, terminal_p.phase[1]);
connect(phase2.terminal_p, terminal_p.phase[2]);
connect(phase3.terminal_p, terminal_p.phase[3]);
connect(phase1.heatPort, heatPort);
connect(phase3.heatPort, heatPort);
connect(phase2.heatPort, heatPort);
end TwoPortResistance;
Model of a resistance with two electrical ports and neutral cable
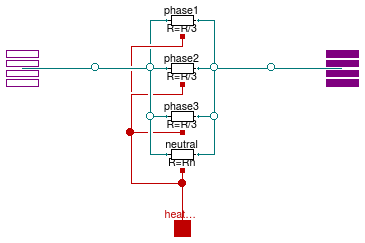
Information
Resistive model that connects two AC three-phase
unbalanced interfaces with neutral line. This model can be used to represent a
cable in a three-phase unbalanced AC system.
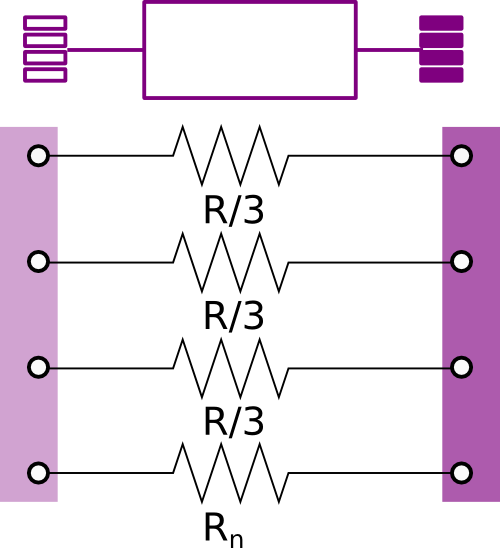
The model represents the lumped resistance as shown in the figure above.
Assuming that the resistance R is the overall resistance of the cable,
each line has a resistance equal to R/3.
The resistance of the neutral cable is defined separately using the parameter
Rn.
Extends from Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network), Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort_N (Partial model interface for a two port component with neutral cable).
Parameters
| Type | Name | Default | Description |
|---|
| Boolean | useHeatPort | false | =true, if HeatPort is enabled |
| Temperature | T | 293.15 | Fixed device temperature if useHeatPort = false [K] |
| Temperature | T_ref | 298.15 | Reference temperature [K] |
| Temperature | M | 507.65 | Temperature constant (R_actual = R*(M + T_heatPort)/(M + T_ref)) [K] |
| Resistance | R | | Resistance at temperature T_ref [Ohm] |
| Resistance | Rn | | Resistance of neutral cable at temperature T_ref [Ohm] |
Connectors
Modelica definition
model TwoPortResistance_N
"Model of a resistance with two electrical ports and neutral cable"
extends Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort;
extends Buildings.Electrical.AC.ThreePhasesUnbalanced.Interfaces.TwoPort_N;
parameter Modelica.SIunits.Temperature T_ref = 298.15
"Reference temperature";
parameter Modelica.SIunits.Temperature M = 507.65
"Temperature constant (R_actual = R*(M + T_heatPort)/(M + T_ref))";
parameter Modelica.SIunits.Resistance R
"Resistance at temperature T_ref";
parameter Modelica.SIunits.Resistance Rn
"Resistance of neutral cable at temperature T_ref";
OnePhase.Lines.TwoPortResistance phase1(
final T_ref=T_ref,
final M=M,
final R=R/3,
final useHeatPort=useHeatPort)
"Resistance line 1";
OnePhase.Lines.TwoPortResistance phase2(
final T_ref=T_ref,
final M=M,
final R=R/3,
final useHeatPort=useHeatPort)
"Resistance line 2";
OnePhase.Lines.TwoPortResistance phase3(
final T_ref=T_ref,
final M=M,
final R=R/3,
final useHeatPort=useHeatPort)
"Resistance line 3";
OnePhase.Lines.TwoPortResistance neutral(
final T_ref=T_ref,
final M=M,
final useHeatPort=useHeatPort,
final R=Rn)
"Resistance neutral cable";
equation
// Joule Losses
LossPower = phase1.LossPower + phase2.LossPower + phase3.LossPower + neutral.LossPower;
connect(terminal_n.phase[1], phase1.terminal_n);
connect(terminal_n.phase[2], phase2.terminal_n);
connect(terminal_n.phase[3], phase3.terminal_n);
connect(phase1.terminal_p, terminal_p.phase[1]);
connect(phase2.terminal_p, terminal_p.phase[2]);
connect(phase3.terminal_p, terminal_p.phase[3]);
connect(phase1.heatPort, heatPort);
connect(phase3.heatPort, heatPort);
connect(phase2.heatPort, heatPort);
connect(neutral.heatPort, heatPort);
connect(neutral.terminal_p, terminal_p.phase[4]);
connect(neutral.terminal_n, terminal_n.phase[4]);
end TwoPortResistance_N;
Automatically generated Mon Jul 13 14:22:59 2015.


 Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.Line
Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.Line
 Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.Line_N
Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.Line_N
 Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.Network
Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.Network
 Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.Network_N
Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.Network_N
 Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortInductance
Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortInductance

 Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortInductance_N
Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortInductance_N

 Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortMatrixRL
Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortMatrixRL
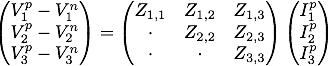
 Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortMatrixRLC
Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortMatrixRLC

 Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortMatrixRLC_N
Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortMatrixRLC_N

 Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortMatrixRL_N
Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortMatrixRL_N
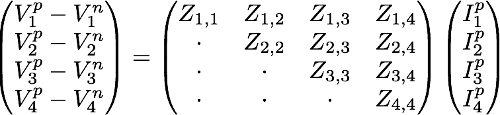
 Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortRL
Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortRL

 Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortRLC
Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortRLC

 Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortRLC_N
Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortRLC_N

 Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortRL_N
Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortRL_N

 Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortResistance
Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortResistance

 Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortResistance_N
Buildings.Electrical.AC.ThreePhasesUnbalanced.Lines.TwoPortResistance_N
