Modelica.Math.Vectors

Information

Library content

This library provides functions operating on vectors:

• toString(v) - returns the string representation of vector v.
• isEqual(v1, v2) - returns true if vectors v1 and v2 have the same size and the same elements.
• norm(v,p) - returns the p-norm of vector v.
• length(v) - returns the length of vector v (= norm(v,2), but inlined and therefore usable in symbolic manipulations)
• normalize(v) - returns vector in direction of v with lenght = 1 and prevents zero-division for zero vector.
• reverse(v) - reverses the vector elements of v.
• sort(v) - sorts the elements of vector v in ascending or descending order.
• find(e, v) - returns the index of the first occurence of scalar e in vector v.
• interpolate(x, y, xi) - returns the interpolated value in (x,y) that corresponds to xi.
• relNodePositions(nNodes) - returns a vector of relative node positions (0..1).

See also

Extends from Modelica.Icons.Package (Icon for standard packages).

Package Content

Name	Description
toString	Convert a real vector in to a string representation
isEqual	Determine if two Real vectors are numerically identical
norm	Return the p-norm of a vector
length	Return length of a vectorReturn length of a vector (better as norm(), if further symbolic processing is performed)
normalize	Return normalized vector such that length = 1 and prevent zero-division for zero vector
reverse	Reverse vector elements (e.g., v[1] becomes last element)
sort	Sort elements of vector in ascending or descending order
find	Find element in a vector
interpolate	Interpolate in a vector
relNodePositions	Return vector of relative node positions (0..1)
Utilities	Utility functions that should not be directly utilized by the user

Modelica.Math.Vectors.toString

Information

Syntax

Vectors.toString(v);
Vectors.toString(v,name="",significantDigits=6);

Description

The function call "Vectors.toString(v)" returns the string representation of vector v. With the optional arguments "name" and "significantDigits" a name and the number of the digits are defined. The default values of "name" and "significantDigits" are "" and 6 respectively. If name=="" (empty string) then the prefix "<name> =" is leaved out at the output-string.

Example

  v = {2.12, -4.34, -2.56, -1.67};
  toString(v);
                         // = "
                         //           2.12
                         //          -4.34
                         //          -2.56
                         //          -1.67"
  toString(v,"vv",1);
                         // = "vv =
                         //           2
                         //          -4
                         //          -3
                         //          -2"

See also

Matrices.toString,

Inputs

Type	Name	Default	Description
Real	v[:]		Real vector
String	name	""	Independent variable name used for printing
Integer	significantDigits	6	Number of significant digits that are shown

Outputs

Type	Name	Description
String	s

Modelica definition

function toString 
  "Convert a real vector in to a string representation"
  import Modelica.Utilities.Strings;

  input Real v[:] "Real vector";
  input String name="" "Independent variable name used for printing";
  input Integer significantDigits=6 
    "Number of significant digits that are shown";
  output String s="";
protected 
  String blanks=Strings.repeat(significantDigits);
  String space=Strings.repeat(8);
  Integer r=size(v, 1);

algorithm 
  if r == 0 then
    s := if name=="" then "[]" else name + " = []";
  else
    s := if name=="" then "\n" else "\n" + name + " = \n";
    for i in 1:r loop
      s := s + space;

      if v[i] >= 0 then
        s := s + " ";
      end if;
      s := s + String(v[i], significantDigits=significantDigits) +
        Strings.repeat(significantDigits + 8 - Strings.length(String(abs(v[i]))));

      s := s + "\n";
    end for;

  end if;

end toString;

Modelica.Math.Vectors.isEqual

Information

Syntax

Vectors.isEqual(v1, v2);
Vectors.isEqual(v1, v2, eps=0);

Description

The function call "Vectors.isEqual(v1, v2)" returns true, if the two Real vectors v1 and v2 have the same dimensions and the same elements. Otherwise the function returns false. Two elements e1 and e2 of the two vectors are checked on equality by the test "abs(e1-e2) ≤ eps", where "eps" can be provided as third argument of the function. Default is "eps = 0".

Example

  Real v1[3] = {1, 2, 3};
  Real v2[3] = {1, 2, 3, 4};
  Real v3[3] = {1, 2, 3.0001};
  Boolean result;
algorithm
  result := Vectors.isEqual(v1,v2);     // = false
  result := Vectors.isEqual(v1,v3);     // = false
  result := Vectors.isEqual(v1,v1);     // = true
  result := Vectors.isEqual(v1,v3,0.1); // = true

See also

Vectors.find, Matrices.isEqual, Strings.isEqual

Extends from Modelica.Icons.Function (Icon for functions).

Inputs

Type	Name	Default	Description
Real	v1[:]		First vector
Real	v2[:]		Second vector (may have different length as v1
Real	eps	0	Two elements e1 and e2 of the two vectors are identical if abs(e1-e2) <= eps

Outputs

Type	Name	Description
Boolean	result	= true, if vectors have the same length and the same elements

Modelica definition

function isEqual 
  "Determine if two Real vectors are numerically identical"
  extends Modelica.Icons.Function;
  input Real v1[:] "First vector";
  input Real v2[:] "Second vector (may have different length as v1";
  input Real eps(min=0) = 0 
    "Two elements e1 and e2 of the two vectors are identical if abs(e1-e2) <= eps";
  output Boolean result 
    "= true, if vectors have the same length and the same elements";

protected 
  Integer n=size(v1, 1) "Dimension of vector v1";
  Integer i=1;
algorithm 
  result := false;
  if size(v2, 1) == n then
    result := true;
    while i <= n loop
      if abs(v1[i] - v2[i]) > eps then
        result := false;
        i := n;
      end if;
      i := i + 1;
    end while;
  end if;
end isEqual;

Modelica.Math.Vectors.norm

Information

Syntax

Vectors.norm(v);
Vectors.norm(v,p=2);   // 1 ≤ p ≤ ∞

Description

The function call "Vectors.norm(v)" returns the Euclidean norm "sqrt(v*v)" of vector v. With the optional second argument "p", any other p-norm can be computed:

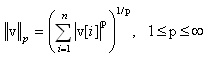
Besides the Euclidean norm (p=2), also the 1-norm and the infinity-norm are sometimes used:

Note, for any vector norm the following inequality holds:

norm(v1+v2,p) ≤ norm(v1,p) + norm(v2,p)

Example

  v = {2, -4, -2, -1};
  norm(v,1);    // = 9
  norm(v,2);    // = 5
  norm(v);      // = 5
  norm(v,10.5); // = 4.00052597412635
  norm(v,Modelica.Constants.inf);  // = 4

See also

Matrices.norm

Extends from Modelica.Icons.Function (Icon for functions).

Inputs

Type	Name	Default	Description
Real	v[:]		Vector
Real	p	2	Type of p-norm (often used: 1, 2, or Modelica.Constants.inf)

Outputs

Type	Name	Description
Real	result	p-norm of vector v

Modelica definition

function norm "Return the p-norm of a vector"
  extends Modelica.Icons.Function;
  input Real v[:] "Vector";
  input Real p(min=1) = 2 
    "Type of p-norm (often used: 1, 2, or Modelica.Constants.inf)";
  output Real result "p-norm of vector v";

algorithm 
  if p == 2 then
    result:=sqrt(v*v);
  elseif p == Modelica.Constants.inf then
    result:=max(abs(v));
  elseif p == 1 then
    result:=sum(abs(v));
  else
    result:=(sum(abs(v[i])^p for i in 1:size(v, 1)))^(1/p);
  end if;
end norm;

Modelica.Math.Vectors.length

Information

Syntax

Vectors.length(v);

Description

The function call "Vectors.length(v)" returns the Euclidean length "sqrt(v*v)" of vector v. The function call is equivalent to Vectors.norm(v). The advantage of length(v) over norm(v)"is that function length(..) is implemented in one statement and therefore the function is usually automatically inlined. Further symbolic processing is therefore possible, which is not the case with function norm(..).

Example

  v = {2, -4, -2, -1};
  length(v);  // = 5

See also

Vectors.norm

Extends from Modelica.Icons.Function (Icon for functions).

Inputs

Type	Name	Default	Description
Real	v[:]		Vector

Outputs

Type	Name	Description
Real	result	Length of vector v

Modelica definition

function length 
  "Return length of a vectorReturn length of a vector (better as norm(), if further symbolic processing is performed)"
  extends Modelica.Icons.Function;
  input Real v[:] "Vector";
  output Real result "Length of vector v";
algorithm 
  result := sqrt(v*v);
end length;

Modelica.Math.Vectors.normalize

Information

Syntax

Vectors.normalize(v);
Vectors.normalize(v,eps=100*Modelica.Constants.eps);

Description

The function call "Vectors.normalize(v)" returns the unit vector "v/length(v)" of vector v. If length(v) is close to zero (more precisely, if length(v) < eps), v/eps is returned in order to avoid a division by zero. For many applications this is useful, because often the unit vector e = v/length(v) is used to compute a vector x*e, where the scalar x is in the order of length(v), i.e., x*e is small, when length(v) is small and then it is fine to replace e by v to avoid a division by zero.

Since the function is implemented in one statement, it is usually inlined and therefore symbolic processing is possible.

Example

  normalize({1,2,3});  // = {0.267, 0.534, 0.802}
  normalize({0,0,0});  // = {0,0,0}

See also

Vectors.length

Extends from Modelica.Icons.Function (Icon for functions).

Inputs

Type	Name	Default	Description
Real	v[:]		Vector
Real	eps	100*Modelica.Constants.eps	if |v| < eps then result = v/eps

Outputs

Type	Name	Description
Real	result[size(v, 1)]	Input vector v normalized to length=1

Modelica definition

function normalize 
  "Return normalized vector such that length = 1 and prevent zero-division for zero vector"
  extends Modelica.Icons.Function;
  input Real v[:] "Vector";
  input Real eps = 100*Modelica.Constants.eps 
    "if |v| < eps then result = v/eps";
  output Real result[size(v, 1)] "Input vector v normalized to length=1";

algorithm 
  result := smooth(0,noEvent(if length(v) >= eps then v/length(v) else v/eps));
end normalize;

Modelica.Math.Vectors.reverse

Information

Syntax

Vectors.reverse(v);

Description

The function call "Vectors.reverse(v)" returns the vector elements in reverse order.

Example

  reverse({1,2,3,4});  // = {4,3,2,1}

Extends from Modelica.Icons.Function (Icon for functions).

Inputs

Type	Name	Default	Description
Real	v[:]		Vector

Outputs

Type	Name	Description
Real	result[size(v, 1)]	Elements of vector v in reversed order

Modelica definition

function reverse 
  "Reverse vector elements (e.g., v[1] becomes last element)"
  extends Modelica.Icons.Function;
  input Real v[:] "Vector";
  output Real result[size(v, 1)] "Elements of vector v in reversed order";

algorithm 
  result := {v[end-i+1] for i in 1:size(v,1)};
end reverse;

Modelica.Math.Vectors.sort

Information

Syntax

           sorted_v = Vectors.sort(v);
(sorted_v, indices) = Vectors.sort(v, ascending=true);

Description

Function sort(..) sorts a Real vector v in ascending order and returns the result in sorted_v. If the optional argument "ascending" is false, the vector is sorted in descending order. In the optional second output argument the indices of the sorted vector with respect to the original vector are given, such that sorted_v = v[indices].

Example

  (v2, i2) := Vectors.sort({-1, 8, 3, 6, 2});
       -> v2 = {-1, 2, 3, 6, 8}
          i2 = {1, 5, 3, 4, 2}

Extends from Modelica.Icons.Function (Icon for functions).

Inputs

Type	Name	Default	Description
Real	v[:]		Vector to be sorted
Boolean	ascending	true	= true if ascending order, otherwise descending order

Outputs

Type	Name	Description
Real	sorted_v[size(v, 1)]	Sorted vector
Integer	indices[size(v, 1)]	sorted_v = v[indices]

Modelica definition

function sort 
  "Sort elements of vector in ascending or descending order"
  extends Modelica.Icons.Function;
  input Real v[:] "Vector to be sorted";
  input Boolean ascending = true 
    "= true if ascending order, otherwise descending order";
  output Real sorted_v[size(v,1)] = v "Sorted vector";
  output Integer indices[size(v,1)] = 1:size(v,1) "sorted_v = v[indices]";

  /* shellsort algorithm; should be improved later */
protected 
  Integer gap;
  Integer i;
  Integer j;
  Real wv;
  Integer wi;
  Integer nv = size(v,1);
  Boolean swap;
algorithm 
  gap := div(nv,2);

  while gap > 0 loop
     i := gap;
     while i < nv loop
        j := i-gap;
        if j>=0 then
           if ascending then
              swap := sorted_v[j+1] > sorted_v[j + gap + 1];
           else
              swap := sorted_v[j+1] < sorted_v[j + gap + 1];
           end if;
        else
           swap := false;
        end if;

        while swap loop
           wv := sorted_v[j+1];
           wi := indices[j+1];
           sorted_v[j+1] := sorted_v[j+gap+1];
           sorted_v[j+gap+1] := wv;
           indices[j+1] := indices[j+gap+1];
           indices[j+gap+1] := wi;
           j := j - gap;
           if j >= 0 then
              if ascending then
                 swap := sorted_v[j+1] > sorted_v[j + gap + 1];
              else
                 swap := sorted_v[j+1] < sorted_v[j + gap + 1];
              end if;
           else
              swap := false;
           end if;
        end while;
        i := i + 1;
     end while;
     gap := div(gap,2);
  end while;
end sort;

Modelica.Math.Vectors.find

Information

Syntax

Vectors.find(e, v);
Vectors.find(e, v, eps=0);

Description

The function call "Vectors.find(e, v)" returns the index of the first occurence of input e in vector v. The test of equality is performed by "abs(e-v[i]) ≤ eps", where "eps" can be provided as third argument of the function. Default is "eps = 0".

Example

  Real v[3] = {1, 2, 3};
  Real e1 = 2;
  Real e2 = 3.01;
  Boolean result;
algorithm
  result := Vectors.find(e1,v);          // = 2
  result := Vectors.find(e2,v);          // = 0
  result := Vectors.find(e2,v,eps=0.1);  // = 3

See also

Vectors.isEqual

Extends from Modelica.Icons.Function (Icon for functions).

Inputs

Type	Name	Default	Description
Real	e		Search for e
Real	v[:]		Integer vector
Real	eps	0	Element e is equal to a element v[i] of vectorv if abs(e-v[i]) <= eps

Outputs

Type	Name	Description
Integer	result	v[result] = e (first occurrence of e); result=0, if not found

Modelica definition

function find "Find element in a vector"
  extends Modelica.Icons.Function;
  input Real e "Search for e";
  input Real v[:] "Integer vector";
  input Real eps(min=0) = 0 
    "Element e is equal to a element v[i] of vectorv if abs(e-v[i]) <= eps";
  output Integer result 
    "v[result] = e (first occurrence of e); result=0, if not found";
protected 
  Integer i;
algorithm 
  result := 0;
  i := 1;
  while i <= size(v, 1) loop
    if abs(v[i]-e)<=eps then
      result := i;
      i := size(v, 1) + 1;
    else
      i := i + 1;
    end if;
  end while;

end find;

Modelica.Math.Vectors.interpolate

Information

Syntax

// Real    x[:], y[:], xi, yi;
// Integer iLast, iNew;
        yi = Vectors.interpolate(x,y,xi);
(yi, iNew) = Vectors.interpolate(x,y,xi,iLast=1);

Description

The function call "Vectors.interpolate(x,y,xi)" interpolates in vectors (x,y) and returns the value yi that corresponds to xi. Vector x[:] must consist of strictly monotonocially increasing values. If xi < x[1] or > x[end], then extrapolation takes places through the first or last two x[:] values, respectively. The search for the interval x[iNew] ≤ xi < x[iNew+1] starts at the optional input argument "iLast". The index "iNew" is returned as output argument. The usage of "iLast" and "iNew" is useful to increase the efficiency of the call, if many interpolations take place.

Example

  Real x[:] = { 0,  2,  4,  6,  8, 10};
  Real y[:] = {10, 20, 30, 40, 50, 60};
algorithm
  (yi, iNew) := Vectors.interpolate(x,y,5);  // yi = 35, iNew=3

Inputs

Type	Name	Default	Description
Real	x[:]		Abszissa table vector (strict monotonically increasing values required)
Real	y[size(x, 1)]		Ordinate table vector
Real	xi		Desired abszissa value
Integer	iLast	1	Index used in last search

Outputs

Type	Name	Description
Real	yi	Ordinate value corresponding to xi
Integer	iNew	xi is in the interval x[iNew] <= xi < x[iNew+1]

Modelica definition

function interpolate "Interpolate in a vector"
  input Real x[ :] 
    "Abszissa table vector (strict monotonically increasing values required)";
  input Real y[ size(x,1)] "Ordinate table vector";
  input Real xi "Desired abszissa value";
  input Integer iLast=1 "Index used in last search";
  output Real yi "Ordinate value corresponding to xi";
  output Integer iNew=1 "xi is in the interval x[iNew] <= xi < x[iNew+1]";
protected 
  Integer i;
  Integer nx=size(x,1);
  Real x1;
  Real x2;
  Real y1;
  Real y2;
algorithm 
  assert(nx > 0, "The table vectors must have at least 1 entry.");
  if nx == 1 then
    yi := y[1];
  else
    // Search interval
    i := min(max(iLast,1),nx-1);
    if xi >= x[i] then
       // search forward
       while i < nx and xi >= x[i] loop
          i := i + 1;
       end while;
       i := i - 1;
    else
       // search backward
       while i > 1 and xi < x[i] loop
          i := i - 1;
       end while;
    end if;

    // Get interpolation data
    x1 := x[i];
    x2 := x[i+1];
    y1 := y[i];
    y2 := y[i+1];

    assert(x2 > x1, "Abszissa table vector values must be increasing");
    // Interpolate
    yi := y1 + (y2 - y1)*(xi - x1)/(x2 - x1);
    iNew :=i;
  end if;

end interpolate;

Modelica.Math.Vectors.relNodePositions

Information

Syntax

Vectors.relNodePositions(nNodes);

Description

The function call "relNodePositions(nNodes)" returns a vector with the relative positions of the nodes of a discretized pipe with nNodes nodes (including the node at the left and at the right side of the pipe), see next figure:

Example

  Real xsi[7];
algorithm
  xsi = relNodePositions(7);  // xsi = {0, 0.1, 0.3, 0.5, 0.7, 0.9, 1}

See also

MultiBody.Visualizers.PipeWithScalarField

Inputs

Type	Name	Default	Description
Integer	nNodes		Number of nodes (including node at left and right position)

Outputs

Type	Name	Description
Real	xsi[nNodes]	Relative node positions

Modelica definition

function relNodePositions 
  "Return vector of relative node positions (0..1)"
  input Integer nNodes 
    "Number of nodes (including node at left and right position)";
  output Real xsi[nNodes] "Relative node positions";
protected 
  Real delta;
algorithm 
  if nNodes >= 1 then
     xsi[1] :=0;
  end if;

  if nNodes >= 2 then
     xsi[nNodes] :=1;
  end if;

  if nNodes == 3 then
     xsi[2] :=0.5;
  elseif nNodes > 3 then
     delta :=1/(nNodes - 2);
     for i in 2:nNodes-1 loop
        xsi[i] :=(i - 1.5)*delta;
     end for;
  end if;

end relNodePositions;