Modelica.Magnetic.FluxTubes.Examples.MovingCoilActuator.Components

Information

Package Content

Name	Description
PermeanceActuator	Detailed actuator model for rough magnetic design of actuator and system simulation
ConstantActuator	Simple behavioural actuator model for system simulation

Modelica.Magnetic.FluxTubes.Examples.MovingCoilActuator.Components.PermeanceActuator

Information

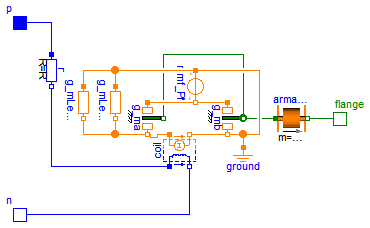
In the ConstantActuator model the force F is strictly proportional to the current i as indicated by the converter constant c. However, there is an additional non-linear force component in such an actuator that is due to the dependency of the coil inductance L on the armature position x. The inductance increases as the armature moves into the stator. The total force is

        1  2 dL
    F = - i  --  + c i
        2    dx

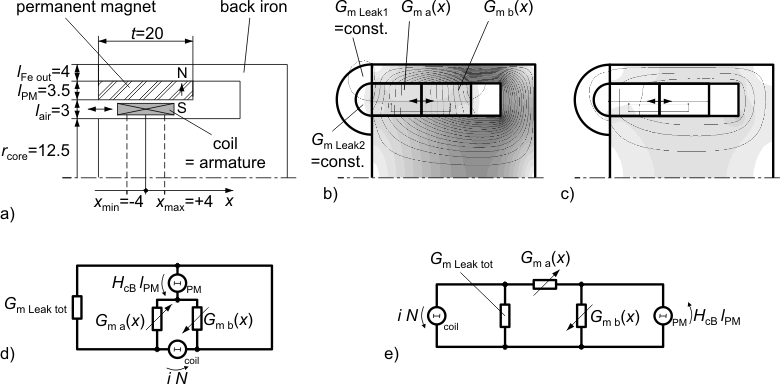
Both force components are properly considered with a simple permeance model as shown in the figures below. Figure (a) illustrates the dimensions of the axisymmetric moving coil actuator that are needed in the permeance model. Figure (b) shows partitioning into flux tubes and the permanent magnetic field without current. G_ma and G_mb both are the permeances resulting from a series connection of the permaent magnet and air gap sections. The field plot of the coil-imposed mmf is shown in figure (c) without the permanent magnetic mmf (H_cB=0). The placement of the magnetic network components in figure (d) retains the geometric structure of the actuator. In figure (e), the permeance model is restructured and thus simplified.

Parameters

Type	Name	Default	Description
Real	N	140	Number of turns
Resistance	R	2.86	Coil resistance [Ohm]
Radius	r_core	12.5e-3	Radius of ferromagnetic stator core [m]
Length	l_PM	3.5e-3	Radial thickness of permanent magnet ring [m]
Length	t	0.02	Axial length of permanent magnet ring and air gap respectively [m]
Length	l_air	3e-3	Total radial length of armature air gap [m]
Length	l_FeOut	4e-3	Radial thickness of outer back iron (for estimation of leakage permeance) [m]
Material
BaseData	material	Modelica.Magnetic.FluxTubes....	Ferromagnetic material characteristics
Armature and stopper
Mass	m_a	0.012	Mass of armature [kg]
TranslationalSpringConstant	c	1e11	Spring stiffness between impact partners [N/m]
TranslationalDampingConstant	d	400	Damping coefficient between impact partners [N.s/m]
Position	x_min	-4e-3	Position of stopper at minimum armature position [m]
Position	x_max	4e-3	Position of stopper at maximum armature position [m]

Connectors

Type	Name	Description
PositivePin	p	Electrical connector
NegativePin	n	Electrical connector
Flange_b	flange	Flange of component

Modelica definition

model PermeanceActuator 
  "Detailed actuator model for rough magnetic design of actuator and system simulation"

  parameter Real N = 140 "Number of turns";
  parameter SI.Resistance R = 2.86 "Coil resistance";

  parameter SI.Radius r_core = 12.5e-3 "Radius of ferromagnetic stator core";

  parameter SI.Length l_PM = 3.5e-3 "Radial thickness of permanent magnet ring";
  parameter SI.Length t = 0.02 
    "Axial length of permanent magnet ring and air gap respectively";

  parameter SI.Length l_air = 3e-3 "Total radial length of armature air gap";

  parameter SI.Length l_FeOut = 4e-3 
    "Radial thickness of outer back iron (for estimation of leakage permeance)";

  parameter Modelica.Magnetic.FluxTubes.Material.HardMagnetic.BaseData
    material=
    Modelica.Magnetic.FluxTubes.Material.HardMagnetic.BaseData() 
    "Ferromagnetic material characteristics";

  parameter SI.Mass m_a = 0.012 "Mass of armature";

  parameter SI.TranslationalSpringConstant c=
        1e11 "Spring stiffness between impact partners";
  parameter SI.TranslationalDampingConstant d=
        400 "Damping coefficient between impact partners";
  parameter SI.Position x_min=-4e-3 
    "Position of stopper at minimum armature position";
  parameter SI.Position x_max=4e-3 
    "Position of stopper at maximum armature position";

  SI.Position x(start = x_min, stateSelect=StateSelect.prefer) 
    "Armature position, alias for flange position";

  SI.Inductance L "Coil inductance";

  Modelica.Magnetic.FluxTubes.Sources.ConstantMagneticPotentialDifference
    mmf_PM(
    final V_m=material.H_cB*l_PM) "Permanent magnet's magnetomotive force";

  Modelica.Magnetic.FluxTubes.Examples.Utilities.TranslatoryArmatureAndStopper
    armature(
    final L=0,
    final m=m_a,
    final c=c,
    final d=d,
    n=2,
    final x_max=x_max,
    final x_min=x_min) 
    "Inertia of moving coil + coil carrier; stoppers at end of stroke range";
  Modelica.Electrical.Analog.Basic.Resistor r(final R=R);

  Basic.Ground ground;
  Modelica.Magnetic.FluxTubes.Basic.ElectroMagneticConverter coil(
                                final N=N);
  Modelica.Magnetic.FluxTubes.Shapes.Force.HollowCylinderRadialFlux
    g_ma(
    final dlBydx=1,
    final l=t/2 + x,
    final r_i=r_core,
    final r_o=r_core + l_air + l_PM,
    final mu_r=1.05,
    final useSupport=false);
  Modelica.Magnetic.FluxTubes.Shapes.Force.HollowCylinderRadialFlux
    g_mb(
    final r_i=r_core,
    final r_o=r_core + l_air + l_PM,
    final dlBydx=-1,
    final l=t/2 - x,
    final mu_r=1.05,
    final useSupport=false);
  Modelica.Magnetic.FluxTubes.Shapes.Leakage.CoaxCylindersEndFaces
    g_mLeak1(
    final r_1=r_core + l_air + l_PM,
    final r_2=r_core + l_air + l_PM + l_FeOut,
    final r_0=r_core) 
    "Leakgage between coaxial end planes of ferromagnetic stator core and outer back iron";
  Modelica.Magnetic.FluxTubes.Shapes.Leakage.HalfCylinder g_mLeak2(
    final l=2*pi*(r_core + (l_air + l_PM)/2)) 
    "Leakgage between edges of ferromagnetic stator core and outer back iron";

  Modelica.Electrical.Analog.Interfaces.PositivePin p "Electrical connector";
  Modelica.Electrical.Analog.Interfaces.NegativePin n "Electrical connector";
  Modelica.Mechanics.Translational.Interfaces.Flange_b flange 
    "Flange of component";
equation 
  x = flange.s;
  L = coil.N^2 * (g_ma.G_m + g_mLeak1.G_m + g_mLeak2.G_m);

  connect(armature.flange_b, flange);
  connect(r.p, p);
  connect(armature.flange_a,g_mb. flange);
  connect(g_mb.flange,g_ma. flange);
  connect(g_mLeak1.port_n, g_ma.port_n);
  connect(g_mLeak2.port_n, g_ma.port_n);
  connect(g_ma.port_n, coil.port_p);
  connect(coil.port_n, g_mb.port_n);
  connect(g_mb.port_n, mmf_PM.port_p);
  connect(mmf_PM.port_p, g_mLeak2.port_p);
  connect(mmf_PM.port_p, g_mLeak1.port_p);
  connect(g_ma.port_p, mmf_PM.port_n);
  connect(mmf_PM.port_n, g_mb.port_p);
  connect(r.n, coil.p);
  connect(coil.n, n);
connect(ground.port, g_mb.port_n);
end PermeanceActuator;

Modelica.Magnetic.FluxTubes.Examples.MovingCoilActuator.Components.ConstantActuator

Information

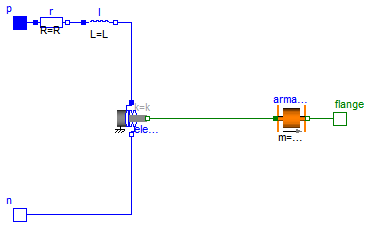
Similar to rotational DC-Motors, the electro-mechanical energy conversion of translatory electrodynamic actuators and generators of moving coil and moving magnet type can be described with the following two converter equations:

      F = c * i
    V_i = c * v

with electrodynamic or Lorentz force F, converter constant c, current i, induced back-emf V_i and armature velocity v. The model is very similar to the well-known behavioural model of a rotational one-phase DC-Machine, except that it is for translatory motion. For a moving coil actuator with a coil inside an air gap with flux density B and a total wire length l inside the magnetic field, the converter constant becomes

    c = B * l.

The converter constant c as well as coil resistance R and inductance L are assumed to be known, e.g., from measurements or catalogue data. Hence this model is well-suited for system simulation together with neighbouring subsystems, but not for actuator design, where the motor constant is to be found on base of the magnetic circuit's geometry, material properties and winding data. See PermeanceActuator for a more accurate model of this actuator that is based on a magnetic network. Due to identical connectors, both models can be used in system simulation, e.g. to simulate a stroke as demonstrated in ArmatureStroke.

Parameters

Type	Name	Default	Description
ElectricalForceConstant	k	3.88	Converter constant [N/A]
Resistance	R	2.86	Coil resistance [Ohm]
Inductance	L	0.0051	Coil inductance at mid-stroke [H]
Armature and stopper
Mass	m_a	0.012	Armature mass [kg]
TranslationalSpringConstant	c	1e11	Spring stiffness between impact partners [N/m]
TranslationalDampingConstant	d	400	Damping coefficient between impact partners [N.s/m]
Position	x_min	-4e-3	Minimum armature position [m]
Position	x_max	4e-3	Maximum armature position [m]

Connectors

Type	Name	Description
PositivePin	p	Electrical connector
NegativePin	n	Electrical connector
Flange_b	flange	Flange of component

Modelica definition

model ConstantActuator 
  "Simple behavioural actuator model for system simulation"

  parameter SI.ElectricalForceConstant k = 3.88 "Converter constant";
  parameter SI.Resistance R = 2.86 "Coil resistance";
  parameter SI.Inductance L = 0.0051 "Coil inductance at mid-stroke";
  parameter SI.Mass m_a = 0.012 "Armature mass";
  parameter Modelica.SIunits.TranslationalSpringConstant c=
        1e11 "Spring stiffness between impact partners";
  parameter Modelica.SIunits.TranslationalDampingConstant d=
        400 "Damping coefficient between impact partners";
  parameter SI.Position x_min = -4e-3 "Minimum armature position";
  parameter SI.Position x_max = 4e-3 "Maximum armature position";

  SI.Position x(start=x_min, stateSelect=StateSelect.prefer) 
    "Armature position, alias for flange position";

  Modelica.Electrical.Analog.Basic.Resistor r(final R=R) "Coil resistance";
  Modelica.Magnetic.FluxTubes.Examples.Utilities.TranslatoryArmatureAndStopper
    armature(
    final m=m_a,
    final x_max=x_max,
    final x_min=x_min,
    final L=0,
    final c=c,
    final d=d,
    n=2) "Armature inertia with stoppers at end of stroke range";

  Modelica.Electrical.Analog.Basic.Inductor l(final L=L) "Coil inductance";
  Modelica.Electrical.Analog.Basic.TranslationalEMF
    electroTranslationalConverter( final k=k);
  Modelica.Electrical.Analog.Interfaces.PositivePin p "Electrical connector";
  Modelica.Electrical.Analog.Interfaces.NegativePin n "Electrical connector";
  Modelica.Mechanics.Translational.Interfaces.Flange_b flange 
    "Flange of component";
equation 
  flange.s = x;

  connect(r.p, p);
  connect(l.p,r. n);
  connect(armature.flange_b, flange);
  connect(l.n, electroTranslationalConverter.p);
  connect(n, electroTranslationalConverter.n);
  connect(electroTranslationalConverter.flange, armature.flange_a);
end ConstantActuator;