Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.HeatTransfer.Channel

Package Content

Name	Description
kc_evenGapLaminar
kc_evenGapOverall
kc_evenGapTurbulent

Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.HeatTransfer.Channel.kc_evenGapLaminar

Calculation of the mean convective heat transfer coefficient kc for a laminar fluid flow through an even gap at different fluid flow and heat transfer situations.

Functions kc_evenGapLaminar and kc_evenGapLaminar_KC

There are basically three differences:

• The function kc_evenGapLaminar is using kc_evenGapLaminar_KC but offers additional output variables like e.g. Reynolds number or Nusselt number and failure status (an output of 1 means that the function is not valid for the inputs).
• Generally the function kc_evenGapLaminar_KC is numerically best used for the calculation of the mean convective heat transfer coefficient kc at known mass flow rate.
• You can perform an inverse calculation from kc_evenGapLaminar_KC, where an unknown mass flow rate is calculated out of a given mean convective heat transfer coefficient kc

Restriction

• laminar regime (Reynolds number ≤ 2200)
• developed fluid flow
• heat transfer from one side of the gap (target=1)
• heat transfer from both sides of the gap (target=2)
• undeveloped fluid flow
• heat transfer from one side of the gap (target=3)
• Prandtl number 0.1 ≤ Pr ≤ 10
• heat transfer from both sides of the gap (target=4)
• Prandtl number 0.1 ≤ Pr ≤ 1000

Geometry

Calculation

The mean convective heat transfer coefficient kc for an even gap is calculated through the corresponding Nusselt number Nu_lam according to [VDI 2002, p. Gb 7, eq. 43] :

    Nu_lam = [(Nu_1)^3 + (Nu_2)^3 + (Nu_3)^3]^(1/3)

with the corresponding mean convective heat transfer coefficient kc :

    kc =  Nu_lam * lambda / d_hyd

with

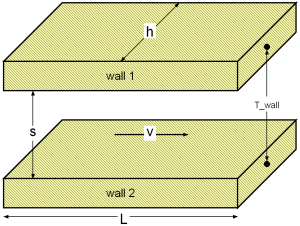
cp	as specific heat capacity at constant pressure [J/(kg.K)],
d_hyd = 2*s	as hydraulic diameter of gap [m],
eta	as dynamic viscosity of fluid [Pa.s],
h	as height of cross sectional area in gap [m],
kc	as mean convective heat transfer coefficient [W/(m2.K)],
lambda	as heat conductivity of fluid [W/(m.K)],
L	as overflowed length of gap (normal to cross sectional area) [m] ,
Nu_lam	as mean Nusselt number [-],
Pr = eta*cp/lambda	as Prandtl number [-],
rho	as fluid density [kg/m3],
s	as distance between parallel plates of cross sectional area [m],
Re = rho*v*d_hyd/eta	as Reynolds number [-],
v	as mean velocity in gap [m/s].

The summands for the mean Nusselt number Nu_lam at a chosen fluid flow and heat transfer situation are calculated as follows:

• developed fluid flow
• heat transfer from one side of the gap (target=1)
• Nu_1 = 4.861
• Nu_2 = 1.841*(Re*Pr*d_hyd/L)^(1/3)
• Nu_3 = 0
• heat transfer from both sides of the gap (target=2)
• Nu_1 = 7.541
• Nu_2 = 1.841*(Re*Pr*d_hyd/L)^(1/3)
• Nu_3 = 0
• undeveloped fluid flow
• heat transfer from one side of the gap (target=3)
• Nu_1 = 4.861
• Nu_2 = 1.841*(Re*Pr*d_hyd/L)^(1/3)
• Nu_3 = [2/(1+22*Pr)]^(1/6)*(Re*Pr*d_hyd/L)^(1/2)
• heat transfer from both sides of the gap (target=4)
• Nu_1 = 7.541
• Nu_2 = 1.841*(Re*Pr*d_hyd/L)^(1/3)
• Nu_3 = [2/(1+22*Pr)]^(1/6)*(Re*Pr*d_hyd/L)^(1/2)

Note that the fluid properties shall be calculated with an arithmetic mean temperature out of the fluid flow temperatures at the entrance and the exit of the gap.

Verification

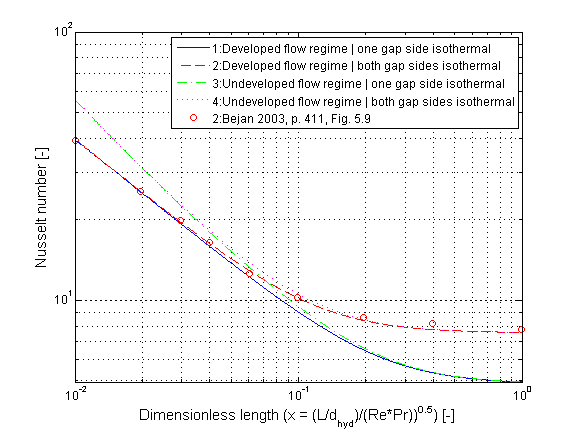
The mean Nusselt number Nu_lam representing the mean convective heat transfer coefficient kc in dependence of the chosen fluid flow and heat transfer situations (targets) is shown in the figure below.

References

Bejan,A.:

Heat transfer handbook. Wiley, 2003.

VDI:

VDI - Wärmeatlas: Berechnungsblätter für den Wärmeübergang. Springer Verlag, 9th edition, 2002.

Extends from Modelica.Icons.Information (Icon for general information packages).

Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.HeatTransfer.Channel.kc_evenGapOverall

Calculation of the mean convective heat transfer coefficient kc for an laminar or turbulent fluid flow through an even gap at different fluid flow and heat transfer situations.

Functions kc_evenGapOverall and kc_evenGapOverall_KC

There are basically three differences:

• The function kc_evenGapOverall is using kc_evenGapOverall_KC but offers additional output variables like e.g. Reynolds number or Nusselt number and failure status (an output of 1 means that the function is not valid for the inputs).
• Generally the function kc_evenGapOverall_KC is numerically best used for the calculation of the mean convective heat transfer coefficient kc at known mass flow rate.
• You can perform an inverse calculation from kc_evenGapOverall_KC, where an unknown mass flow rate is calculated out of a given mean convective heat transfer coefficient kc

Restriction

• developed fluid flow
• heat transfer from one side of the gap (target=1)
• heat transfer from both sides of the gap (target=2)
• undeveloped fluid flow
• heat transfer from one side of the gap (target=3)
• Prandtl number 0.1 ≤ Pr ≤ 10
• heat transfer from both sides of the gap (target=4)
• Prandtl number 0.1 ≤ Pr ≤ 1000
• turbulent regime always calculated for developed fluid flow and heat transfer from both sides of the gap (target=2)

Geometry and Calculation

This heat transfer function enables a calculation of heat transfer coefficient for laminar and turbulent flow regime. The geometry, constant and fluid parameters of the function are the same as for kc_evenGapLaminar and kc_evenGapTurbulent.

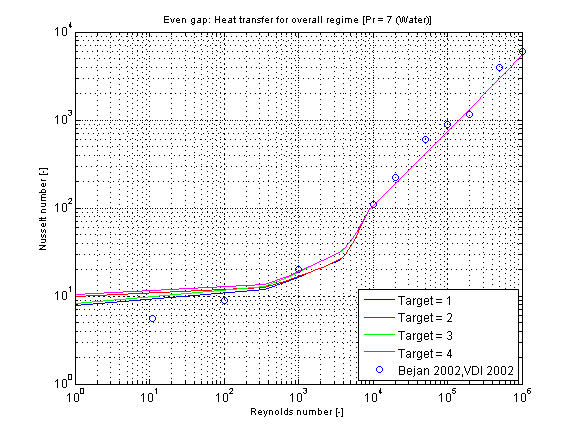
The calculation conditions for laminar and turbulent flow is equal to the calculation in kc_evenGapLaminar and kc_evenGapTurbulent. A smooth transition between both functions is carried out between 2200 ≤ Re ≤ 30000 (see figure below).

Verification

The mean Nusselt number Nu representing the mean convective heat transfer coefficient kc for Prandtl numbers of different fluids in dependence of the chosen fluid flow and heat transfer situations (targets) is shown in the figures below.

• Target 1: Developed fluid flow and heat transfer from one side of the gap
• Target 2: Developed fluid flow and heat transfer from both sides of the gap
• Target 3: Undeveloped fluid flow and heat transfer from one side of the gap
• Target 4: Undeveloped fluid flow and heat transfer from both sides of the gap

The verification for all targets is shown in the following figure w.r.t. the reference:

References

Bejan,A.:

Heat transfer handbook. Wiley, 2003.

VDI:

VDI - Wärmeatlas: Berechnungsblätter für den Wärmeübergang. Springer Verlag, 9th edition, 2002.

Extends from Modelica.Icons.Information (Icon for general information packages).

Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.HeatTransfer.Channel.kc_evenGapTurbulent

Calculation of the mean convective heat transfer coefficient kc for a developed turbulent fluid flow through an even gap at heat transfer from both sides.

Functions kc_evenGapTurbulent and kc_evenGapTurbulent_KC

There are basically three differences:

• The function kc_evenGapTurbulent is using kc_evenGapTurbulent_KC but offers additional output variables like e.g. Reynolds number or Nusselt number and failure status (an output of 1 means that the function is not valid for the inputs).
• Generally the function kc_evenGapTurbulent_KC is numerically best used for the calculation of the mean convective heat transfer coefficient kc at known mass flow rate.
• You can perform an inverse calculation from kc_evenGapTurbulent_KC, where an unknown mass flow rate is calculated out of a given mean convective heat transfer coefficient kc

Restriction

• identical and constant wall tempertures
• hydraulic diameter per gap lenght (d_hyd / L) ≤ 1
• 0.5 ≤ Prandtl number Pr ≤ 100)
• turbulent regime (3e4 ≤ Reynolds number ≤ 1e6)
• developed fluid flow
• heat transfer from both sides of the gap (Target = 2)

Geometry

Calculation

The mean convective heat transfer coefficient kc for an even gap is calculated through the corresponding Nusselt number Nu_turb according to Gnielinski in [VDI 2002, p. Gb 7, sec. 2.4]

    Nu_turb =(zeta/8)*Re*Pr/{1+12.7*[zeta/8]^(0.5)*[Pr^(2/3) -1]}*{1+[d_hyd/L]^(2/3)}

where the pressure loss coefficient zeta according to Konakov in [VDI 2002, p. Ga 5, eq. 27] is determined by

    zeta =  1/[1.8*log10(Re) - 1.5]^2

resulting to the corresponding mean convective heat transfer coefficient kc

    kc =  Nu_turb * lambda / d_hyd

with

cp	as specific heat capacity at constant pressure [J/(kg.K)],
d_hyd = 2*s	as hydraulic diameter of gap [m],
eta	as dynamic viscosity of fluid [Pa.s],
h	as height of cross sectional area in gap [m],
kc	as mean convective heat transfer coefficient [W/(m2.K)],
lambda	as heat conductivity of fluid [W/(m.K)],
L	as overflowed length of gap (normal to cross sectional area) [m] ,
Nu_turb	as mean Nusselt number for turbulent regime [-],
Pr = eta*cp/lambda	as Prandtl number [-],
rho	as fluid density [kg/m3],
s	as distance between parallel plates of cross sectional area [m],
Re = rho*v*d_hyd/eta	as Reynolds number [-],
v	as mean velocity in gap [m/s],
zeta	as pressure loss coefficient [-].

Note that the fluid flow properties shall be calculated with an arithmetic mean temperature out of the fluid flow temperatures at the entrance and the exit of the gap.

Verification

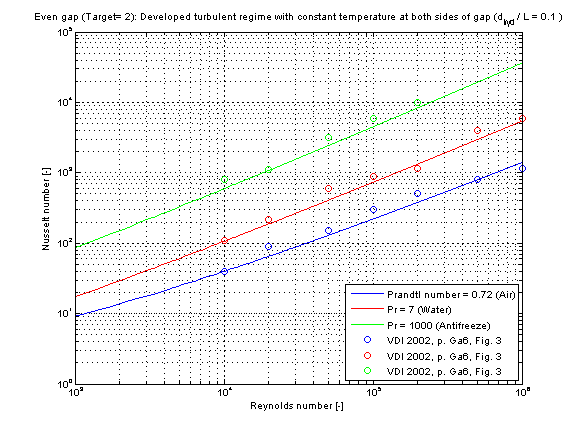
The mean Nusselt number Nu_turb representing the mean convective heat transfer coefficient kc in dependence of the chosen fluid flow and heat transfer situations (targets) is shown in the figure below.

• Target 2: Developed fluid flow and heat transfer from both sides of the gap

References

VDI:

VDI - Wärmeatlas: Berechnungsblätter für den Wärmeübergang. Springer Verlag, 9th edition, 2002.

Extends from Modelica.Icons.Information (Icon for general information packages).