Modelica.Electrical.Machines.BasicMachines.Components

Information

Extends from Modelica.Icons.Package (Icon for standard packages).

Package Content

Name	Description
PartialAirGap	Partial airgap model
AirGapS	Airgap in stator-fixed coordinate system
AirGapR	Airgap in rotor-fixed coordinate system
Inductor	Space phasor inductor
SquirrelCage	Squirrel Cage
DamperCage	Squirrel Cage
ElectricalExcitation	Electrical excitation
PermanentMagnet	Permanent magnet excitation
InductorDC	Ideal linear electrical inductor for electrical DC machines
PartialAirGapDC	Partial airgap model of a DC machine
AirGapDC	Linear airgap model of a DC machine
CompoundDCExcitation	Compound excitation = shunt + series
PartialCore	Partial model of transformer core with 3 windings
IdealCore	Ideal transformer with 3 windings
BasicTransformer	Partial model of threephase transformer

Modelica.Electrical.Machines.BasicMachines.Components.PartialAirGap

Information

Parameters

Type	Name	Default	Description
Integer	m	3	Number of phases
Integer	p		Number of pole pairs

Connectors

Type	Name	Description
Flange_a	flange
Flange_a	support	Support at which the reaction torque is acting
SpacePhasor	spacePhasor_s
SpacePhasor	spacePhasor_r

Modelica definition

partial model PartialAirGap "Partial airgap model"
  parameter Integer m=3 "Number of phases";
  parameter Integer p(min=1) "Number of pole pairs";
  output Modelica.SIunits.Torque tauElectrical;
  Modelica.SIunits.Angle gamma "Rotor displacement angle";
  Modelica.SIunits.Current i_ss[2] 
    "Stator current space phasor with respect to the stator fixed frame";
  Modelica.SIunits.Current i_sr[2] 
    "Stator current space phasor with respect to the rotor fixed frame";
  Modelica.SIunits.Current i_rs[2] 
    "Rotor current space phasor with respect to the stator fixed frame";
  Modelica.SIunits.Current i_rr[2] 
    "Rotor current space phasor with respect to the rotor fixed frame";
  Modelica.SIunits.MagneticFlux psi_ms[2] 
    "Magnetizing flux phasor with respect to the stator fixed frame";
  Modelica.SIunits.MagneticFlux psi_mr[2] 
    "Magnetizing flux phasor with respect to the rotor fixed frame";
  Real RotationMatrix[2,2] "Matrix of rotation from rotor to stator";
public 
  Modelica.Mechanics.Rotational.Interfaces.Flange_a flange;
  Modelica.Mechanics.Rotational.Interfaces.Flange_a support 
    "Support at which the reaction torque is acting";
  Machines.Interfaces.SpacePhasor spacePhasor_s;
  Machines.Interfaces.SpacePhasor spacePhasor_r;
equation 
  // mechanical angle of the rotor of an equivalent 2-pole machine
  gamma=p*(flange.phi-support.phi);
  RotationMatrix={{+cos(gamma),-sin(gamma)},{+sin(gamma),+cos(gamma)}};
  i_ss = spacePhasor_s.i_;
  i_ss = RotationMatrix*i_sr;
  i_rr = spacePhasor_r.i_;
  i_rs = RotationMatrix*i_rr;
  // Stator voltage induction
  spacePhasor_s.v_ = der(psi_ms);
  // Rotor voltage induction
  spacePhasor_r.v_ = der(psi_mr);
  // Electromechanical torque (cross product of current and flux space phasor)
  tauElectrical = m/2*p*(spacePhasor_s.i_[2]*psi_ms[1] - spacePhasor_s.i_[1]*psi_ms[2]);
  flange.tau = -tauElectrical;
  support.tau = tauElectrical;
end PartialAirGap;

Modelica.Electrical.Machines.BasicMachines.Components.AirGapS

Information

Extends from PartialAirGap (Partial airgap model).

Parameters

Type	Name	Default	Description
Inductance	Lm		Main field inductance [H]
Integer	m	3	Number of phases
Integer	p		Number of pole pairs

Connectors

Type	Name	Description
Flange_a	flange
Flange_a	support	Support at which the reaction torque is acting
SpacePhasor	spacePhasor_s
SpacePhasor	spacePhasor_r

Modelica definition

model AirGapS "Airgap in stator-fixed coordinate system"
  parameter Modelica.SIunits.Inductance Lm "Main field inductance";
  extends PartialAirGap;
  Modelica.SIunits.Current i_ms[2] 
    "Magnetizing current space phasor with respect to the stator fixed frame";
protected 
  parameter Modelica.SIunits.Inductance L[2,2]={{Lm,0},{0,Lm}} 
    "Inductance matrix";
equation 
  // Magnetizing current with respect to the stator reference frame
  i_ms = i_ss + i_rs;
  // Magnetizing flux linkage with respect to the stator reference frame
  psi_ms = L*i_ms;
  // Magnetizing flux linkage with respect to the rotor reference frame
  psi_mr = transpose(RotationMatrix)*psi_ms;
end AirGapS;

Modelica.Electrical.Machines.BasicMachines.Components.AirGapR

Information

Extends from PartialAirGap (Partial airgap model).

Parameters

Type	Name	Default	Description
Inductance	Lmd		Main field inductance d-axis [H]
Inductance	Lmq		Main field inductance q-axis [H]
Integer	m	3	Number of phases
Integer	p		Number of pole pairs

Connectors

Type	Name	Description
Flange_a	flange
Flange_a	support	Support at which the reaction torque is acting
SpacePhasor	spacePhasor_s
SpacePhasor	spacePhasor_r

Modelica definition

model AirGapR "Airgap in rotor-fixed coordinate system"
  parameter Modelica.SIunits.Inductance Lmd "Main field inductance d-axis";
  parameter Modelica.SIunits.Inductance Lmq "Main field inductance q-axis";
  extends PartialAirGap;
  Modelica.SIunits.Current i_mr[2] 
    "Magnetizing current space phasor with respect to the rotor fixed frame";
protected 
  parameter Modelica.SIunits.Inductance L[2,2]={{Lmd,0},{0,Lmq}} 
    "Inductance matrix";
equation 
  // Magnetizing current with respect to the rotor reference frame
  i_mr = i_sr + i_rr;
  // Main flux linkage with respect to the rotor reference frame
  psi_mr = L*i_mr;
  // Main flux linkage with respect to the stator reference frame
  psi_ms = RotationMatrix*psi_mr;
end AirGapR;

Modelica.Electrical.Machines.BasicMachines.Components.Inductor

Information

Parameters

Type	Name	Default	Description
Inductance	L[2]		Inductance of both axes [H]

Connectors

Type	Name	Description
SpacePhasor	spacePhasor_a
SpacePhasor	spacePhasor_b

Modelica definition

model Inductor "Space phasor inductor"
  parameter Modelica.SIunits.Inductance L[2] "Inductance of both axes";
  Modelica.SIunits.Voltage v_[2];
  Modelica.SIunits.Current i_[2];
  Machines.Interfaces.SpacePhasor spacePhasor_a;
  Machines.Interfaces.SpacePhasor spacePhasor_b;
equation 
  spacePhasor_a.i_ + spacePhasor_b.i_ = zeros(2);
  v_ = spacePhasor_a.v_ - spacePhasor_b.v_;
  i_ = spacePhasor_a.i_;
  v_[1] = L[1]*der(i_[1]);
  v_[2] = L[2]*der(i_[2]);
end Inductor;

Modelica.Electrical.Machines.BasicMachines.Components.SquirrelCage

Information

Model of a squirrel cage / symmetrical damper cage in two axis.

The squirrel cage has an optional (conditional) HeatPort, which can be enabled or disabled by the Boolean parameter useHeatPort. Temperatures of both axis are the same, both losses are added. Material properties alpha of both axis are the same.

Extends from Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network).

Parameters

Type	Name	Default	Description
Inductance	Lrsigma		Rotor stray inductance per phase translated to stator [H]
Resistance	Rr		Rotor resistance per phase translated to stator at T_ref [Ohm]
Temperature	T_ref	293.15	Reference temperature [K]
LinearTemperatureCoefficient	alpha	0	Temperature coefficient of resistance at T_ref [1/K]
Boolean	useHeatPort	false	=true, if HeatPort is enabled
Temperature	T	T_ref	Fixed device temperature if useHeatPort = false [K]

Connectors

Type	Name	Description
HeatPort_a	heatPort
SpacePhasor	spacePhasor_r

Modelica definition

model SquirrelCage "Squirrel Cage"
  parameter Modelica.SIunits.Inductance Lrsigma 
    "Rotor stray inductance per phase translated to stator";
  parameter Modelica.SIunits.Resistance Rr 
    "Rotor resistance per phase translated to stator at T_ref";
  parameter Modelica.SIunits.Temperature T_ref=293.15 "Reference temperature";
  parameter Modelica.SIunits.LinearTemperatureCoefficient alpha=0 
    "Temperature coefficient of resistance at T_ref";
  extends Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort(T = T_ref);
  Modelica.SIunits.Resistance Rr_actual 
    "Actual resistance = Rr*(1 + alpha*(T_heatPort - T_ref))";
  Machines.Interfaces.SpacePhasor spacePhasor_r;
equation 
  assert((1 + alpha*(T_heatPort - T_ref)) >= Modelica.Constants.eps, "Temperature outside scope of model!");
  Rr_actual = Rr*(1 + alpha*(T_heatPort - T_ref));
  spacePhasor_r.v_ = Rr_actual*spacePhasor_r.i_ + Lrsigma*der(spacePhasor_r.i_);
  2/3*LossPower = Rr_actual*(spacePhasor_r.i_[1]*spacePhasor_r.i_[1] + spacePhasor_r.i_[2]*spacePhasor_r.i_[2]);
end SquirrelCage;

Modelica.Electrical.Machines.BasicMachines.Components.DamperCage

Information

Model of an usymmetrical damper cage in two axis.

The damper cage has an optional (conditional) HeatPort, which can be enabled or disabled by the Boolean parameter useHeatPort. Temperatures of both axis are the same, both losses are added. Material properties alpha can be set differently for both d- and q-axis, although reference temperature for both resistances is the same.

Extends from Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network).

Parameters

Type	Name	Default	Description
Inductance	Lrsigmad		Stray inductance in d-axis per phase translated to stator [H]
Inductance	Lrsigmaq		Stray inductance in q-axis per phase translated to stator [H]
Resistance	Rrd		Resistance in d-axis per phase translated to stator at T_ref [Ohm]
Resistance	Rrq		Resistance in q-axis per phase translated to stator at T_ref [Ohm]
Temperature	T_ref	293.15	Reference temperature of both resistances in d- and q-axis [K]
LinearTemperatureCoefficient	alpha	0	Temperature coefficient of both resistances in d- and q-axis at T_ref [1/K]
Boolean	useHeatPort	false	=true, if HeatPort is enabled
Temperature	T	T_ref	Fixed device temperature if useHeatPort = false [K]

Connectors

Type	Name	Description
HeatPort_a	heatPort
SpacePhasor	spacePhasor_r

Modelica definition

model DamperCage "Squirrel Cage"
  parameter Modelica.SIunits.Inductance Lrsigmad 
    "Stray inductance in d-axis per phase translated to stator";
  parameter Modelica.SIunits.Inductance Lrsigmaq 
    "Stray inductance in q-axis per phase translated to stator";
  parameter Modelica.SIunits.Resistance Rrd 
    "Resistance in d-axis per phase translated to stator at T_ref";
  parameter Modelica.SIunits.Resistance Rrq 
    "Resistance in q-axis per phase translated to stator at T_ref";
  parameter Modelica.SIunits.Temperature T_ref=293.15 
    "Reference temperature of both resistances in d- and q-axis";
  parameter Modelica.SIunits.LinearTemperatureCoefficient alpha=0 
    "Temperature coefficient of both resistances in d- and q-axis at T_ref";
  extends Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort(T = T_ref);
  Modelica.SIunits.Resistance Rrd_actual 
    "Actual resistance = Rrd*(1 + alpha*(T_heatPort - T_ref))";
  Modelica.SIunits.Resistance Rrq_actual 
    "Actual resistance = Rrq*(1 + alpha*(T_heatPort - T_ref))";
  Machines.Interfaces.SpacePhasor spacePhasor_r;
equation 
  assert((1 + alpha*(T_heatPort - T_ref)) >= Modelica.Constants.eps, "Temperature outside scope of model!");
  Rrd_actual = Rrd*(1 + alpha*(T_heatPort - T_ref));
  Rrq_actual = Rrq*(1 + alpha*(T_heatPort - T_ref));
  spacePhasor_r.v_[1] = Rrd_actual * spacePhasor_r.i_[1] + Lrsigmad * der(spacePhasor_r.i_[1]);
  spacePhasor_r.v_[2] = Rrq_actual * spacePhasor_r.i_[2] + Lrsigmaq * der(spacePhasor_r.i_[2]);
  2/3*LossPower = Rrd_actual*spacePhasor_r.i_[1]*spacePhasor_r.i_[1] + Rrq_actual*spacePhasor_r.i_[2]*spacePhasor_r.i_[2];
end DamperCage;

Modelica.Electrical.Machines.BasicMachines.Components.ElectricalExcitation

Information

Parameters

Type	Name	Default	Description
Real	turnsRatio		Ratio stator current / excitation current

Connectors

Type	Name	Description
SpacePhasor	spacePhasor_r
PositivePin	pin_ep
NegativePin	pin_en

Modelica definition

model ElectricalExcitation "Electrical excitation"
  parameter Real turnsRatio(start=1) 
    "Ratio stator current / excitation current";
  Modelica.SIunits.Current ie "Excitation current";
  Modelica.SIunits.Voltage ve "Excitation voltage";
  Machines.Interfaces.SpacePhasor spacePhasor_r;
  Modelica.Electrical.Analog.Interfaces.PositivePin pin_ep;
  Modelica.Electrical.Analog.Interfaces.NegativePin pin_en;
equation 
  pin_ep.i + pin_en.i = 0;
  ie = +pin_ep.i;
  ve = pin_ep.v - pin_en.v;
  spacePhasor_r.i_ = {-ie*turnsRatio,0};
  ve = spacePhasor_r.v_[1]*turnsRatio*3/2;
end ElectricalExcitation;

Modelica.Electrical.Machines.BasicMachines.Components.PermanentMagnet

Information

Parameters

Type	Name	Default	Description
Current	Ie		Equivalent excitation current [A]

Connectors

Type	Name	Description
SpacePhasor	spacePhasor_r

Modelica definition

model PermanentMagnet "Permanent magnet excitation"
  parameter Modelica.SIunits.Current Ie "Equivalent excitation current";
  Machines.Interfaces.SpacePhasor spacePhasor_r;
equation 
  spacePhasor_r.i_ = {-Ie,0};
end PermanentMagnet;

Modelica.Electrical.Machines.BasicMachines.Components.InductorDC

Information

The linear inductor connects the branch voltage v with the branch current i by v = L * di/dt. If quasiStationary == false, the electrical transients are neglected, i.e., the voltage drop is zero.

Extends from Modelica.Electrical.Analog.Interfaces.OnePort (Component with two electrical pins p and n and current i from p to n).

Parameters

Type	Name	Default	Description
Inductance	L		Inductance [H]
Boolean	quasiStationary		No electrical transients if true

Connectors

Type	Name	Description
PositivePin	p	Positive pin (potential p.v > n.v for positive voltage drop v)
NegativePin	n	Negative pin

Modelica definition

model InductorDC 
  "Ideal linear electrical inductor for electrical DC machines"
  extends Modelica.Electrical.Analog.Interfaces.OnePort;
  parameter Modelica.SIunits.Inductance L(start=1) "Inductance";
  parameter Boolean quasiStationary(start=false) 
    "No electrical transients if true";
equation 
  v = if quasiStationary then 0 else L*der(i);
end InductorDC;

Modelica.Electrical.Machines.BasicMachines.Components.PartialAirGapDC

Information

Parameters

Type	Name	Default	Description
Boolean	quasiStationary		No electrical transients if true
Real	turnsRatio		Ratio of armature turns over number of turns of the excitation winding

Connectors

Type	Name	Description
Flange_a	flange
Flange_a	support	Support at which the reaction torque is acting
PositivePin	pin_ap
PositivePin	pin_ep
NegativePin	pin_an
NegativePin	pin_en

Modelica definition

partial model PartialAirGapDC "Partial airgap model of a DC machine"
  parameter Boolean quasiStationary(start=false) 
    "No electrical transients if true";
  parameter Real turnsRatio 
    "Ratio of armature turns over number of turns of the excitation winding";
  output Modelica.SIunits.AngularVelocity w "Angluar velocity";
  Modelica.SIunits.Voltage vei 
    "Voltage drop across field excitation inductance";
  Modelica.SIunits.Current ie "Excitation current";
  Modelica.SIunits.MagneticFlux psi_e "Excitation flux";
  Modelica.SIunits.Voltage vai "Induced armature voltage";
  Modelica.SIunits.Current ia "Armature current";
  output Modelica.SIunits.Torque tauElectrical;
  Modelica.Mechanics.Rotational.Interfaces.Flange_a flange;
  Modelica.Mechanics.Rotational.Interfaces.Flange_a support 
    "Support at which the reaction torque is acting";
  Modelica.Electrical.Analog.Interfaces.PositivePin pin_ap;
  Modelica.Electrical.Analog.Interfaces.PositivePin pin_ep;
  Modelica.Electrical.Analog.Interfaces.NegativePin pin_an;
  Modelica.Electrical.Analog.Interfaces.NegativePin pin_en;
equation 
  // armature pins
  vai = pin_ap.v - pin_an.v;
  ia = + pin_ap.i;
  ia = - pin_an.i;
  // excitation pins
  vei = pin_ep.v - pin_en.v;
  ie = + pin_ep.i;
  ie = - pin_en.i;
  // induced voltage across field excitation inductance
  vei = if quasiStationary then 0 else der(psi_e);
  // mechanical speed
  w = der(flange.phi)-der(support.phi);
  // induced armature voltage
  vai = turnsRatio * psi_e * w;
  // electrical torque (ia is perpendicular to flux)
  tauElectrical = turnsRatio * psi_e * ia;
  flange.tau = -tauElectrical;
  support.tau = tauElectrical;
end PartialAirGapDC;

Modelica.Electrical.Machines.BasicMachines.Components.AirGapDC

Information

Extends from PartialAirGapDC (Partial airgap model of a DC machine).

Parameters

Type	Name	Default	Description
Boolean	quasiStationary		No electrical transients if true
Real	turnsRatio		Ratio of armature turns over number of turns of the excitation winding
Inductance	Le		Excitation inductance [H]

Connectors

Type	Name	Description
Flange_a	flange
Flange_a	support	Support at which the reaction torque is acting
PositivePin	pin_ap
PositivePin	pin_ep
NegativePin	pin_an
NegativePin	pin_en

Modelica definition

model AirGapDC "Linear airgap model of a DC machine"
  extends PartialAirGapDC;
  parameter Modelica.SIunits.Inductance Le "Excitation inductance";
equation 
  // excitation flux: linearly dependent on excitation current
  psi_e = Le * ie;
end AirGapDC;

Modelica.Electrical.Machines.BasicMachines.Components.CompoundDCExcitation

Information

Parameters

Type	Name	Default	Description
Real	excitationTurnsRatio		Ratio of series excitation turns over shunt excitation turns

Connectors

Type	Name	Description
PositivePin	pin_p	Positive pin to airgap
NegativePin	pin_n	Negative pin to airgap
PositivePin	pin_ep	Positive pin to shunt excitation
NegativePin	pin_en	Negative pin to shunt excitation
PositivePin	pin_sep	Positive pin to series excitation
NegativePin	pin_sen	Negative pin to series excitation

Modelica definition

model CompoundDCExcitation "Compound excitation = shunt + series"
  parameter Real excitationTurnsRatio 
    "Ratio of series excitation turns over shunt excitation turns";
  Modelica.SIunits.Voltage v = pin_p.v - pin_n.v;
  Modelica.SIunits.Current i = pin_p.i;
  Modelica.SIunits.Voltage ve = pin_ep.v - pin_en.v;
  Modelica.SIunits.Current ie = pin_ep.i;
  Modelica.SIunits.Voltage vse = pin_sep.v - pin_sen.v;
  Modelica.SIunits.Current ise = pin_sep.i;
  Modelica.Electrical.Analog.Interfaces.PositivePin pin_p 
    "Positive pin to airgap";
  Modelica.Electrical.Analog.Interfaces.NegativePin pin_n 
    "Negative pin to airgap";
  Modelica.Electrical.Analog.Interfaces.PositivePin pin_ep 
    "Positive pin to shunt excitation";
  Modelica.Electrical.Analog.Interfaces.NegativePin pin_en 
    "Negative pin to shunt excitation";
  Modelica.Electrical.Analog.Interfaces.PositivePin pin_sep 
    "Positive pin to series excitation";
  Modelica.Electrical.Analog.Interfaces.NegativePin pin_sen 
    "Negative pin to series excitation";
equation 
//current balances
  pin_p.i + pin_n.i = 0;
  pin_ep.i + pin_en.i = 0;
  pin_sep.i + pin_sen.i = 0;
//compound currents
  -i = ie + excitationTurnsRatio*ise;
//induced voltages
  ve = v;
  vse = v*excitationTurnsRatio;
end CompoundDCExcitation;

Modelica.Electrical.Machines.BasicMachines.Components.PartialCore

Information

Parameters

Type	Name	Default	Description
Integer	m	3	Number of phases
Real	n12		Turns ratio 1:2
Real	n13		Turns ratio 1:3

Connectors

Type	Name	Description
PositivePlug	plug_p1
NegativePlug	plug_n1
PositivePlug	plug_p2
NegativePlug	plug_n2
PositivePlug	plug_p3
NegativePlug	plug_n3

Modelica definition

partial model PartialCore 
  "Partial model of transformer core with 3 windings"
  parameter Integer m(final min=1) = 3 "Number of phases";
  parameter Real n12(start=1) "Turns ratio 1:2";
  parameter Real n13(start=1) "Turns ratio 1:3";
  Modelica.SIunits.Voltage v1[m] = plug_p1.pin.v  - plug_n1.pin.v;
  Modelica.SIunits.Current i1[m] = plug_p1.pin.i;
  Modelica.SIunits.Voltage v2[m] = plug_p2.pin.v  - plug_n2.pin.v;
  Modelica.SIunits.Current i2[m] = plug_p2.pin.i;
  Modelica.SIunits.Voltage v3[m] = plug_p3.pin.v  - plug_n3.pin.v;
  Modelica.SIunits.Current i3[m] = plug_p3.pin.i;
  Modelica.SIunits.Current im[m] = i1 + i2/n12 + i3/n13 "Magnetizing current";
  Modelica.Electrical.MultiPhase.Interfaces.PositivePlug plug_p1(final m=
        m);
  Modelica.Electrical.MultiPhase.Interfaces.NegativePlug plug_n1(final m=
        m);
  Modelica.Electrical.MultiPhase.Interfaces.PositivePlug plug_p2(final m=
        m);
  Modelica.Electrical.MultiPhase.Interfaces.NegativePlug plug_n2(final m=
        m);
  Modelica.Electrical.MultiPhase.Interfaces.PositivePlug plug_p3(final m=
        m);
  Modelica.Electrical.MultiPhase.Interfaces.NegativePlug plug_n3(final m=
        m);
equation 
  plug_p1.pin.i + plug_n1.pin.i = zeros(m);
  plug_p2.pin.i + plug_n2.pin.i = zeros(m);
  plug_p3.pin.i + plug_n3.pin.i = zeros(m);
end PartialCore;

Modelica.Electrical.Machines.BasicMachines.Components.IdealCore

Information

Extends from PartialCore (Partial model of transformer core with 3 windings).

Parameters

Type	Name	Default	Description
Integer	m	3	Number of phases
Real	n12		Turns ratio 1:2
Real	n13		Turns ratio 1:3

Connectors

Type	Name	Description
PositivePlug	plug_p1
NegativePlug	plug_n1
PositivePlug	plug_p2
NegativePlug	plug_n2
PositivePlug	plug_p3
NegativePlug	plug_n3

Modelica definition

model IdealCore "Ideal transformer with 3 windings"

  extends PartialCore;
equation 
  im = zeros(m);
  v1 = n12*v2;
  v1 = n13*v3;
end IdealCore;

Modelica.Electrical.Machines.BasicMachines.Components.BasicTransformer

Information

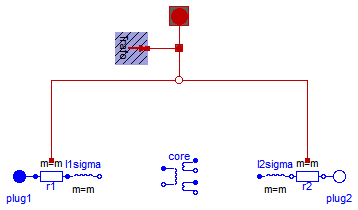
Extends from Machines.Interfaces.PartialBasicTransformer (Partial model of threephase transformer).

Parameters

Type	Name	Default	Description
Real	n		Ratio primary voltage (line-to-line) / secondary voltage (line-to-line)
Boolean	useThermalPort	false	Enable / disable (=fixed temperatures) thermal port
Operational temperatures
Temperature	T1Operational		Operational temperature of primary resistance [K]
Temperature	T2Operational		Operational temperature of secondary resistance [K]
Nominal resistances and inductances
Resistance	R1		Primary resistance per phase at TRef [Ohm]
Temperature	T1Ref		Reference temperature of primary resistance [K]
LinearTemperatureCoefficient20	alpha20_1		Temperature coefficient of primary resistance at 20 degC [1/K]
Inductance	L1sigma		Primary stray inductance per phase [H]
Resistance	R2		Secondary resistance per phase at TRef [Ohm]
Temperature	T2Ref		Reference temperature of secondary resistance [K]
LinearTemperatureCoefficient20	alpha20_2		Temperature coefficient of secondary resistance at 20 degC [1/K]
Inductance	L2sigma		Secondary stray inductance per phase [H]

Connectors

Type	Name	Description
PositivePlug	plug1	Primary plug
NegativePlug	plug2	Secondary plug
ThermalPortTransformer	thermalPort

Modelica definition

partial model BasicTransformer 
  "Partial model of threephase transformer"
  extends Machines.Interfaces.PartialBasicTransformer;
//dummy will be removed when conversion script is applicable
end BasicTransformer;