Modelica.Electrical.Analog.Lines

Lossy and lossless segmented transmission lines, and LC distributed line models

Information




This package contains lossy and lossless segmented transmission lines,
and LC distributed line models.

The line models do not yet possess a conditional heating port.





Extends from Modelica.Icons.Library (Icon for library).

Package Content




NameDescription


Modelica.Electrical.Analog.Lines.OLine OLine
Lossy Transmission Line


Modelica.Electrical.Analog.Lines.M_OLine M_OLine
multiple OLine


Modelica.Electrical.Analog.Lines.ULine ULine
Lossy RC Line


Modelica.Electrical.Analog.Lines.TLine1 TLine1
Lossless transmission line with characteristic impedance Z0 and transmission delay TD


Modelica.Electrical.Analog.Lines.TLine2 TLine2
Lossless transmission line with characteristic impedance Z0, frequency F and normalized length NL


Modelica.Electrical.Analog.Lines.TLine3 TLine3
Lossless transmission line with characteristic impedance Z0 and frequency F








Modelica.Electrical.Analog.Lines.OLine
Modelica.Electrical.Analog.Lines.OLine

Lossy Transmission Line

Modelica.Electrical.Analog.Lines.OLine

Information





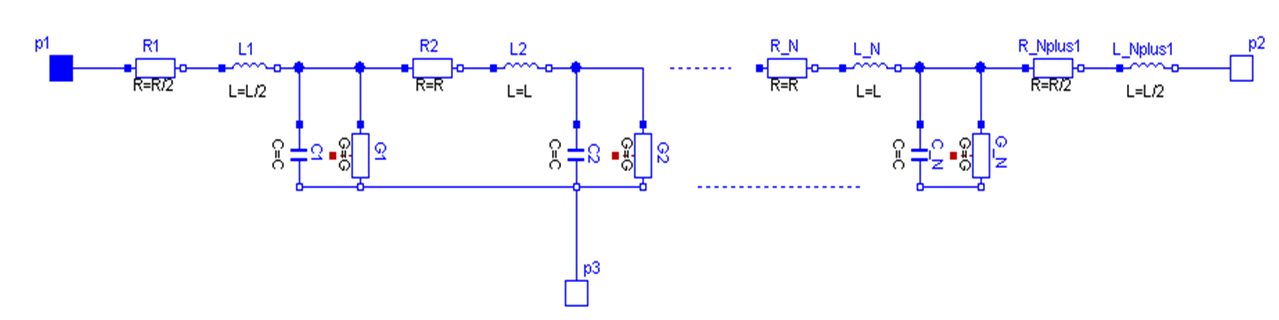
Lossy Transmission Line.
  As can be seen in the picture below, the lossy transmission line OLine consists of segments of
  lumped resistances and inductances in series
  and conductances and capacitances that are
  connected with the reference pin p3. The precision
  of the model depends on the number N of
  lumped segments.


To get a symmetric line model, the first resistor and inductor are cut into two parts (R1 and R_Nplus1, L1 and L_Nplus1)

The two new resistors and inductors have the half of the resistance/inductance the original resistor/inductor had. 

The resistor R1/inductor L1 are at the beginning of the line and R_Nplus1/L_Nplu1 are at the end of the line.


model Analog.Lines.OLine


The values of the capacitances are calculated with: C=c*length/N with c given by the user, "lenght=length of line" and "N=number of segments".

The values of the conductances are calculated in the same way the capacitances are, but with g instead of c.

The values of the resistors and inductors are calculated with :R=r*length/(N+1) and L=l*length/(N+1).

For all capacitances, conductances, resistors and inductances the values of each segment are the same exept

of the first and last resistor and inductor, that only have the half of the value of the rest.

Note, this is different to the lumped line model of SPICE.





References:


  Johnson, B.; Quarles, T.; Newton, A. R.; Pederson, D. O.;
  Sangiovanni-Vincentelli, A.: SPICE3 Version 3e User's Manual
  (April 1, 1991). Department of Electrical Engineering and
  Computer Sciences, University of California, Berkley
  p. 12, p. 106 - 107








Parameters




TypeNameDefaultDescription


Realr Resistance per meter [Ohm/m]


Reall Inductance per meter [H/m]


Realg Conductance per meter [S/m]


Realc Capacitance per meter [F/m]


Lengthlength Length of line [m]


IntegerN Number of lumped segments




Connectors




TypeNameDescription


Pinp1 


Pinp2 


Pinp3 




Modelica definition


model OLine "Lossy Transmission Line"
  //extends Interfaces.ThreePol;
  Interfaces.Pin p1;
  Interfaces.Pin p2;
  Interfaces.Pin p3;
  SI.Voltage v13;
  SI.Voltage v23;
  SI.Current i1;
  SI.Current i2;
  parameter Real r(
    final min=Modelica.Constants.small,
    unit="Ohm/m", start=1) "Resistance per meter";
  parameter Real l(
    final min=Modelica.Constants.small,
    unit="H/m", start=1) "Inductance per meter";
  parameter Real g(
    final min=Modelica.Constants.small,
    unit="S/m", start=1) "Conductance per meter";
  parameter Real c(
    final min=Modelica.Constants.small,
    unit="F/m", start=1) "Capacitance per meter";
  parameter SI.Length length(final min=Modelica.Constants.small, start=1) 
    "Length of line";
  parameter Integer N(final min=1, start=1) "Number of lumped segments";
protected 
  Basic.Resistor R[N + 1](R=fill(r*length/(N + 1), N + 1));
  Basic.Inductor L[N + 1](L=fill(l*length/(N + 1), N + 1));
  Basic.Capacitor C[N](C=fill(c*length/(N), N));
  Basic.Conductor G[N](G=fill(g*length/(N), N));
equation 
  v13 = p1.v - p3.v;
  v23 = p2.v - p3.v;
  i1 = p1.i;
  i2 = p2.i;
  connect(p1, R[1].p);
  for i in 1:N loop
    connect(R[i].n, L[i].p);
    connect(L[i].n, C[i].p);
    connect(L[i].n, G[i].p);
    connect(C[i].n, p3);
    connect(G[i].n, p3);
    connect(L[i].n, R[i + 1].p);
  end for;
  connect(R[N + 1].n, L[N + 1].p);
  connect(L[N + 1].n, p2);
end OLine;







Modelica.Electrical.Analog.Lines.M_OLine
Modelica.Electrical.Analog.Lines.M_OLine

multiple OLine

Modelica.Electrical.Analog.Lines.M_OLine

Information





The M_OLine is a multi line model  which consists of several segements and several single lines.
Each segement consists of resistors and inductors that are connected in series in each single line, and of capacitors and conductors both between the lines and to the ground. The inductors are coupled to each other like in the M_Inductor model. The following picture shows the schematic of a segment with four single lines (lines=4):






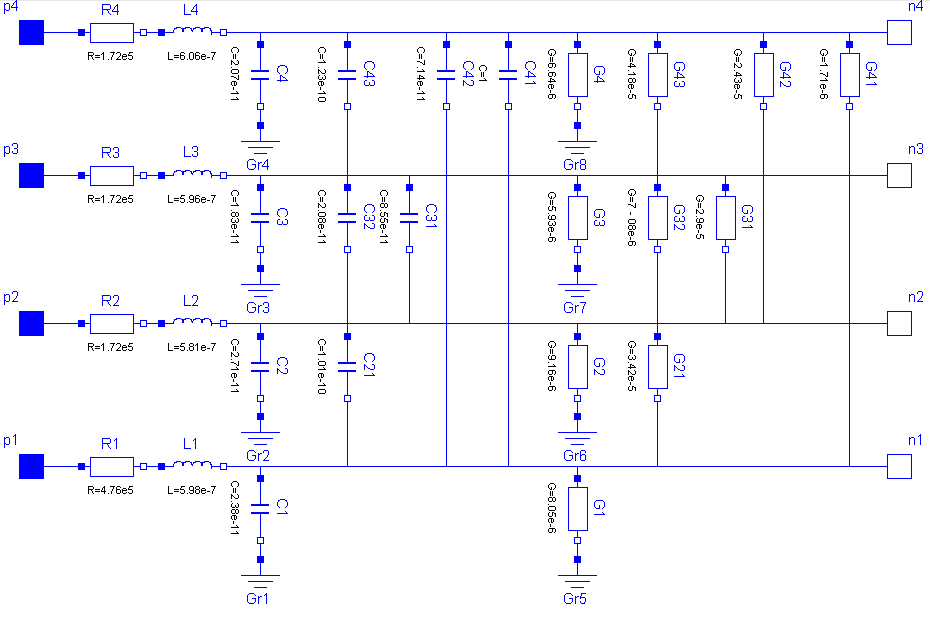
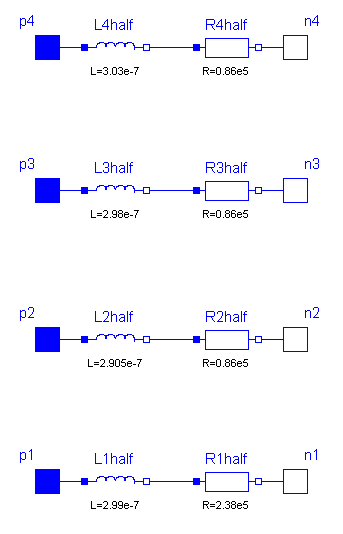
model Analog.Lines.M_OLine




The complete multi line consists of N segments and an auxiliary segment_last:





-- segment_1 -- segment_2 -- ... -- segment_N -- segment_last -- 






In the picture of the segment can be seen, that a single segment is unsymmetric. Connecting such unsymmetric segments in a series forces also an unsymmetric multi line. To get a symmetric model which
is useful for coupling and which guaranties the same pin properties, in the segment_1 only half valued resistors and inductors are used. The remaining resistors and inductors are at the other end of the line within the auxiliary segment_last. For the example with 4 lines the schematic of segment_last is like this:





model Analog.Lines.M_OLine




 The number of the capacitors
and conductors depends on the number of single lines that are used, because each line is connected to every other line by both a capacitor and a conductor. One line consists of at least two segements.



Inside the model M_OLine the model segment is used. This model represents one segment which is build as described above. For modelling the inductances and their mutual couplings the model M_Transformer is used.


To fill the resistance vector, resistance values as many as lines are needed, e.g. if there are four lines,
four resistances are needed. For example for a microelectronic line of 0.1m lenght, a sensible resistance-vector
would be R=[4.76e5, 1.72e5, 1.72e5, 1.72e5].



Filling the matrixes of the inductances, capacitances and conductances is a bit more complicated, because
those components occur also between two lines and not only (like the resistor) in one line. The entries of
the matrices are given by the user in form of a vector. The  vector length dim_vector_lgc is calculated by  dim_vector_lgc = lines*(lines+1)/2. Inside the model a symmetric inductance matrix, a symmetric capacitance matrix and
a symmetric conductance matrix are build out of the entries of the vectors given by the user. The way of building
is the same for each matrix, so the approach for filling one of the matrices will be shown at an example:


The number of lines is assumed to be four. To build the matrix, the model needs the values from the main diagonal and from 
the positions that are below the main diagonal. To get the following matrix








  

    
    
    1
    0.1
    0.2
    0.4
  

  

    Matrix
    =
    0.1
    2
    0.3
    0.5
  

  

    
    
    0.2
    0.3
    3
    0.6
  

  

    
    
    0.4
    0.5
    0.6
    4
  





the vector with dim_vector_lgc=4*5/2=10 has to appear in the following way: vector = [1, 0.1, 0.2, 0.4, 2, 0.3 0.5, 3, 0.6, 4]




For the example of a microelectronic line of 0.1m lenght, which is used as default example for the M_OLine model, a sensible inductance-matrix would be




  

    
    
    5.98e-7
    4.44e-7
    4.39e-7
    3.99e-7
  

  

    L
    =
    4.44e-7
    5.81e-7
    4.09e-7
    4.23e-7
  

  

    
    
    4.39e-7
    4.09e-7
    5.96e-7
    4.71e-7
  

  

    
    
    3.99e-7
    4.23e-7
    4.71e-7
    6.06e-7
  









For the example of a microelectronic line of 0.1m lenght, which is used as default example for the M_OLine model, a sensible capacitance-matrix would be




  

    
    
    2.38e-11
    1.01e-10
    8.56e-11
    5.09e-12
  

  

    C
    =
    1.01e-10
    2.71e-11
    2.09e-11
    7.16e-11
  

  

    
    
    8.56e-11
    2.09e-11
    1.83e-11
    1.23e-10
  

  

    
    
    5.09e-12
    7.16e-11
    1.23e-10
    2.07e-11
  









For the example of a microelectronic line of 0.1m lenght, which is used as default example for the M_OLine model, a sensible conductance-matrix would be




  

    
    
    8.05e-6
    3.42e-5
    2.91e-5
    1.76e-5
  

  

    G
    =
    3.42e-5
    9.16e-6
    5.93e-6
    6.64e-6
  

  

    
    
    2.90e-5
    7.08e-6
    5.93e-6
    4.19e-5
  

  

    
    
    1.71e-6
    2.43e-5
    4.18e-5
    6.64e-6
  











Parameters




TypeNameDefaultDescription


Lengthlength0.1Length of line [m]


IntegerN5Number of lumped segments


Integerlines4Number of lines


Realr[lines]{4.76e5,1.72e5,1.72e5,1.72e5}Resistance per meter [Ohm/m]


Reall[dim_vector_lgc]{5.98e-7,4.44e-7,4.39e-7,3.9...Inductance per meter [H/m]


Realg[dim_vector_lgc]{8.05e-6,3.42e-5,2 - 91e-5,1...Conductance per meter [S/m]


Realc[dim_vector_lgc]{2.38e-11,1.01e-10,8.56e-11,...Capacitance per meter [F/m]




Connectors




TypeNameDescription


PositivePinp[lines]Positive pin


NegativePinn[lines]Negative pin




Modelica definition


model M_OLine "multiple OLine"

  parameter Modelica.SIunits.Length length(final min=Modelica.Constants.small) = 0.1 
    "Length of line";
  parameter Integer N(final min=1) = 5 "Number of lumped segments";
  parameter Integer lines(final min=2) = 4 "Number of lines";
protected 
  parameter Integer dim_vector_lgc=div(lines*(lines+1),2);
public 
  parameter Real r[lines](
    final min=Modelica.Constants.small,
    unit="Ohm/m") = {4.76e5,1.72e5,1.72e5,1.72e5} "Resistance per meter";

  parameter Real l[dim_vector_lgc](
    final min=Modelica.Constants.small,
    unit="H/m") = {5.98e-7,4.44e-7,4.39e-7,3.99e-7,5.81e-7,4.09e-7,4.23e-7,5.96e-7,4.71e-7,
        6.06e-7} "Inductance per meter";

  parameter Real g[dim_vector_lgc](
    final min=Modelica.Constants.small,
    unit="S/m") = {8.05e-6,3.42e-5,2 - 91e-5,1.76e-6,9.16e-6,7.12e-6,2.43e-5,5.93e-6,
        4.19e-5,6.64e-6} "Conductance per meter";

  parameter Real c[dim_vector_lgc](
    final min=Modelica.Constants.small,
    unit="F/m") = {2.38e-11,1.01e-10,8.56e-11,5.09e-12,2.71e-11,2.09e-11,7.16e-11,1.83e-11,
        1.23e-10,2.07e-11} "Capacitance per meter";

model segment

  parameter Integer lines(final min=1)=3;       //number of lines
  parameter Integer dim_vector_lgc=div(lines*(lines+1),2);
  Modelica.Electrical.Analog.Interfaces.PositivePin p[lines] "Positive pin";
  Modelica.Electrical.Analog.Interfaces.NegativePin n[lines] "Negative pin";

  parameter Real Cl[dim_vector_lgc]=fill(1,dim_vector_lgc);
  parameter Real Rl[lines]=fill(7,lines);
  parameter Real Ll[dim_vector_lgc]=fill(2,dim_vector_lgc);
  parameter Real Gl[dim_vector_lgc]= fill(1,dim_vector_lgc);

  Modelica.Electrical.Analog.Basic.Capacitor C[dim_vector_lgc](C=Cl);
  Modelica.Electrical.Analog.Basic.Resistor R[lines](R=Rl);
  Modelica.Electrical.Analog.Basic.Conductor G[dim_vector_lgc](G=Gl);
  Modelica.Electrical.Analog.Basic.M_Transformer inductance(N=lines, L=Ll);
  Modelica.Electrical.Analog.Basic.Ground M;

equation 
  for j in 1:lines-1 loop

    connect(R[j].p,p[j]);
    connect(R[j].n,inductance.p[j]);
    connect(inductance.n[j],n[j]);
    connect(inductance.n[j],C[((1+(j-1)*lines)-((j-2)*(j-1))*0.5)].p);
    connect(C[((1+(j-1)*lines)-((j-2)*(j-1))*0.5)].n,M.p);
    connect(inductance.n[j],G[((1+(j-1)*lines)-((j-2)*(j-1))*0.5)].p);
    connect(G[((1+(j-1)*lines)-((j-2)*(j-1))*0.5)].n,M.p);

    for i in j+1:lines loop
      connect(inductance.n[j],C[((1+(j-1)*lines)-((j-2)*(j-1))*0.5)+1+i-(j+1)].p);
      connect(C[((1+(j-1)*lines)-((j-2)*(j-1))*0.5)+1+i-(j+1)].n,inductance.n[i]);
      connect(inductance.n[j],G[((1+(j-1)*lines)-((j-2)*(j-1))*0.5)+1+i-(j+1)].p);
      connect(G[((1+(j-1)*lines)-((j-2)*(j-1))*0.5)+1+i-(j+1)].n,inductance.n[i]);
    end for;
  end for;
    connect(R[lines].p,p[lines]);
    connect(R[lines].n,inductance.p[lines]);
    connect(inductance.n[lines],n[lines]);
    connect(inductance.n[lines],C[dim_vector_lgc].p);
    connect(C[dim_vector_lgc].n,M.p);
    connect(inductance.n[lines],G[dim_vector_lgc].p);
    connect(G[dim_vector_lgc].n,M.p);

end segment;

model segment_last

  Modelica.Electrical.Analog.Interfaces.PositivePin p[lines] "Positive pin";
  Modelica.Electrical.Analog.Interfaces.NegativePin n[lines] "Negative pin";
  parameter Integer lines(final min=1)=3;
  parameter Integer dim_vector_lgc= div(lines*(lines+1),2);
  parameter Real Rl[lines]=fill(1,lines);
  parameter Real Ll[dim_vector_lgc]=fill(1,dim_vector_lgc);
  Modelica.Electrical.Analog.Basic.Resistor R[lines](R=Rl);
  Modelica.Electrical.Analog.Basic.M_Transformer inductance(  N=lines, L=Ll);
  Modelica.Electrical.Analog.Basic.Ground M;

equation 
  for j in 1:lines-1 loop

    connect(p[j],inductance.p[j]);
    connect(inductance.n[j],R[j].p);
    connect(R[j].n,n[j]);
  end for;
    connect(p[lines],inductance.p[lines]);
    connect(inductance.n[lines],R[lines].p);
    connect(R[lines].n,n[lines]);

end segment_last;

  segment s[N - 1](
    lines=fill(lines, N - 1),
    dim_vector_lgc=fill(dim_vector_lgc, N - 1),
    Rl=fill(r*length/N, N - 1),
    Ll=fill(l*length/N, N - 1),
    Cl=fill(c*length/N, N - 1),
    Gl=fill(g*length/N, N - 1));
  segment s_first(
    lines=lines,
    dim_vector_lgc=dim_vector_lgc,
    Rl=r*length/(2*N),
    Cl=c*length/(N),
    Ll=l*length/(2*N),
    Gl=g*length/(N));
  segment_last s_last(
    lines=lines,
    Rl=r*length/(2*N),
    Ll=l*length/(2*N));
  Modelica.Electrical.Analog.Interfaces.PositivePin p[lines] "Positive pin";
  Modelica.Electrical.Analog.Interfaces.NegativePin n[lines] "Negative pin";

equation 
    connect(p,s_first.p);
    connect(s_first.n,s[1].p);
  for i in 1:N-2 loop
    connect(s[i].n,s[i+1].p);
  end for;
    connect(s[N-1].n,s_last.p);
    connect(s_last.n,n);

end M_OLine;







Modelica.Electrical.Analog.Lines.ULine
Modelica.Electrical.Analog.Lines.ULine

Lossy RC Line

Modelica.Electrical.Analog.Lines.ULine

Information





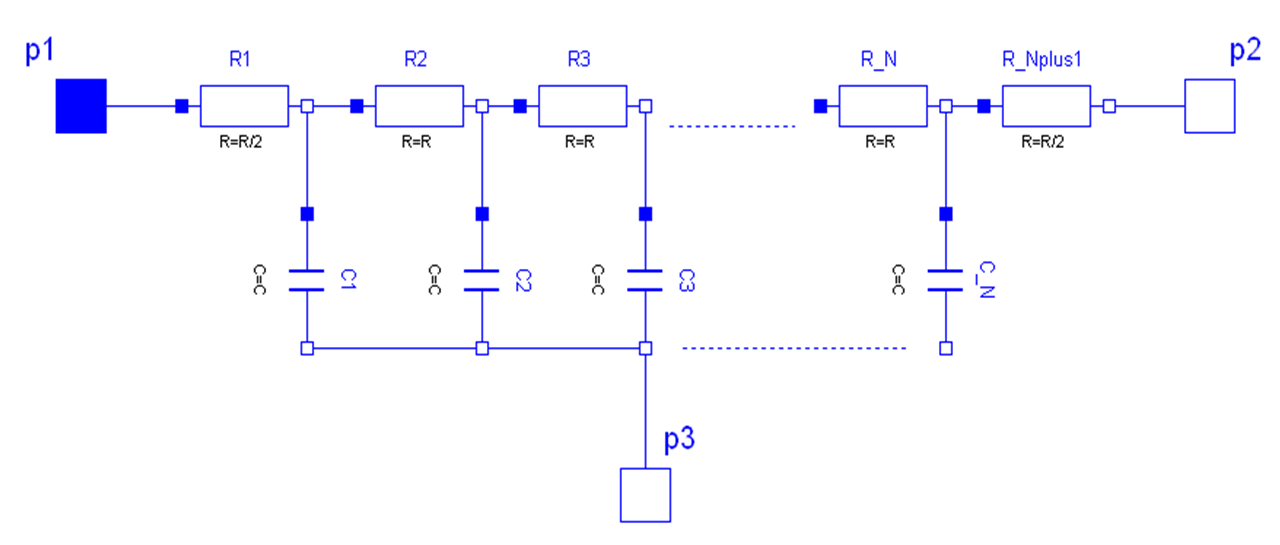
As can be seen in the picture below, the lossy RC line ULine consists of segments of
lumped series resistances and capacitances that are
connected with the reference pin p3. 
The precision
of the model depends on the number N of
lumped segments.


To get a symmetric line model, the first Resistor is cut into two parts (R1 and R_Nplus1)

The two new resistors have the half of the resistance of the original Resistor had. The Resistor R1

is at the beginning of the line and R_Nplus1 is at the end of the line.


model Analog.Lines.ULine


The values of the capacitances are calculated with: C=c*length/N with c given by the user, "lenght=length of line" and "N=number of segments".

The values of the resistors are calculated with :R=r*length/(N+1).

For all capacitances and resistors the values of each segment are the same exept

of the first and last resistor, that only hase the half of the value of the other resistors.

Note, this is different to the lumped line model of SPICE.


References





 Johnson, B.; Quarles, T.; Newton, A. R.; Pederson, D. O.;
    Sangiovanni-Vincentelli, A.


 SPICE3 Version 3e User's Manual
    (April 1, 1991). Department of Electrical Engineering and
    Computer Sciences, University of California, Berkley
    p. 22, p. 124







Parameters




TypeNameDefaultDescription


Realr Resistance per meter [Ohm/m]


Realc Capacitance per meter [F/m]


Lengthlength Length of line [m]


IntegerN Number of lumped segments




Connectors




TypeNameDescription


Pinp1 


Pinp2 


Pinp3 




Modelica definition


model ULine "Lossy RC Line"
  //extends Interfaces.ThreePol;
  Interfaces.Pin p1;
  Interfaces.Pin p2;
  Interfaces.Pin p3;
  SI.Voltage v13;
  SI.Voltage v23;
  SI.Current i1;
  SI.Current i2;
  parameter Real r(
    final min=Modelica.Constants.small,
    unit="Ohm/m", start=1) "Resistance per meter";
  parameter Real c(
    final min=Modelica.Constants.small,
    unit="F/m", start=1) "Capacitance per meter";
  parameter SI.Length length(final min=Modelica.Constants.small, start=1) 
    "Length of line";
  parameter Integer N(final min=1, start=1) "Number of lumped segments";
protected 
  Basic.Resistor R[N + 1](R=fill(r*length/(N + 1), N + 1));
  Basic.Capacitor C[N](C=fill(c*length/(N), N));
equation 
  v13 = p1.v - p3.v;
  v23 = p2.v - p3.v;
  i1 = p1.i;
  i2 = p2.i;
  connect(p1, R[1].p);
  for i in 1:N loop
    connect(R[i].n, R[i + 1].p);
  end for;
  for i in 1:N loop
    connect(R[i].n, C[i].p);
  end for;
  for i in 1:N loop
    connect(C[i].n, p3);
  end for;
  connect(R[N + 1].n, p2);
end ULine;







Modelica.Electrical.Analog.Lines.TLine1
Modelica.Electrical.Analog.Lines.TLine1

Lossless transmission line with characteristic impedance Z0 and transmission delay TD

Modelica.Electrical.Analog.Lines.TLine1

Information





Lossless transmission line with characteristic impedance Z0 and transmission delay TD
  The lossless transmission line TLine1 is a two Port. Both port branches
  consist of a resistor with characteristic impedance Z0 and a controled voltage
  source that takes into consideration the transmission delay TD.
  For further details see Branin's article below.
  The model parameters can be derived from inductance and
  capacitance per length (L' resp. C'), i. e.
  Z0 = sqrt(L'/C') and TD = sqrt(L'*C')*length_of_line. Resistance R'
  and conductance C' per meter are assumed to be zero.






References:





Branin Jr., F. H.


 Transient Analysis of Lossless Transmission Lines.
     Proceedings of the IEEE 55(1967), 2012 - 2013


 Hoefer, E. E. E.; Nielinger, H.


 SPICE : Analyseprogramm fuer elektronische
  Schaltungen. Springer-Verlag, Berlin, Heidelberg, New York, Tokyo, 1985.







Extends from Modelica.Electrical.Analog.Interfaces.TwoPort (Component with two electrical ports, including current).

Parameters




TypeNameDefaultDescription


ResistanceZ0 Characteristic impedance [Ohm]


TimeTD Transmission delay [s]




Connectors




TypeNameDescription


PositivePinp1Positive pin of the left port (potential p1.v > n1.v for positive voltage drop v1)


NegativePinn1Negative pin of the left port


PositivePinp2Positive pin of the right port (potential p2.v > n2.v for positive voltage drop v2)


NegativePinn2Negative pin of the right port




Modelica definition


model TLine1 
  "Lossless transmission line with characteristic impedance Z0 and transmission delay TD"

  extends Modelica.Electrical.Analog.Interfaces.TwoPort;
  parameter Modelica.SIunits.Resistance Z0(start=1) "Characteristic impedance";
  parameter Modelica.SIunits.Time TD(start=1) "Transmission delay";
protected 
  Modelica.SIunits.Voltage er;
  Modelica.SIunits.Voltage es;
equation 
  assert(Z0 > 0, "Z0 has to be positive");
  assert(TD > 0, "TD has to be positive");
  i1 = (v1 - es)/Z0;
  i2 = (v2 - er)/Z0;
  es = 2*delay(v2, TD) - delay(er, TD);
  er = 2*delay(v1, TD) - delay(es, TD);
end TLine1;







Modelica.Electrical.Analog.Lines.TLine2
Modelica.Electrical.Analog.Lines.TLine2

Lossless transmission line with characteristic impedance Z0, frequency F and normalized length NL

Modelica.Electrical.Analog.Lines.TLine2

Information





Lossless transmission line with characteristic impedance Z0, frequency F and normalized length NL
  The lossless transmission line TLine2 is a two Port. Both port branches
  consist of a resistor with the value of the characteristic impedance Z0
  and a controled voltage source that takes into consideration
  the transmission delay.
  For further details see Branin's article below.
  Resistance R' and conductance C' per meter are assumed to be zero.
  The characteristic impedance Z0 can be derived from inductance and
  capacitance per length (L' resp. C'), i. e. Z0 = sqrt(L'/C').
  The normalized length NL is equal to the length of the line divided
  by the wavelength corresponding to the frequency F, i. e. the
  transmission delay TD is the quotient of NL and F.






References:





Branin Jr., F. H.


 Transient Analysis of Lossless Transmission Lines.
     Proceedings of the IEEE 55(1967), 2012 - 2013


 Hoefer, E. E. E.; Nielinger, H.


 SPICE : Analyseprogramm fuer elektronische
  Schaltungen. Springer-Verlag, Berlin, Heidelberg, New York, Tokyo, 1985.







Extends from Modelica.Electrical.Analog.Interfaces.TwoPort (Component with two electrical ports, including current).

Parameters




TypeNameDefaultDescription


ResistanceZ0 Characteristic impedance [Ohm]


FrequencyF Frequency [Hz]


RealNL Normalized length




Connectors




TypeNameDescription


PositivePinp1Positive pin of the left port (potential p1.v > n1.v for positive voltage drop v1)


NegativePinn1Negative pin of the left port


PositivePinp2Positive pin of the right port (potential p2.v > n2.v for positive voltage drop v2)


NegativePinn2Negative pin of the right port




Modelica definition


model TLine2 
  "Lossless transmission line with characteristic impedance Z0, frequency F and normalized length NL"

  extends Modelica.Electrical.Analog.Interfaces.TwoPort;
  parameter Modelica.SIunits.Resistance Z0(start=1) "Characteristic impedance";
  parameter Modelica.SIunits.Frequency F(start=1) "Frequency";
  parameter Real NL(start=1) "Normalized length";
protected 
  Modelica.SIunits.Voltage er;
  Modelica.SIunits.Voltage es;
  Modelica.SIunits.Time TD;
equation 
  assert(Z0 > 0, "Z0 has to be positive");
  assert(NL > 0, "NL has to be positive");
  assert(F > 0, "F  has to be positive");
  TD = NL/F;
  i1 = (v1 - es)/Z0;
  i2 = (v2 - er)/Z0;
  es = 2*delay(v2, TD) - delay(er, TD);
  er = 2*delay(v1, TD) - delay(es, TD);
end TLine2;







Modelica.Electrical.Analog.Lines.TLine3
Modelica.Electrical.Analog.Lines.TLine3

Lossless transmission line with characteristic impedance Z0 and frequency F

Modelica.Electrical.Analog.Lines.TLine3

Information





Lossless transmission line with characteristic impedance Z0 and frequency F
  The lossless transmission line TLine3 is a two Port. Both port branches
  consist of a resistor with value of the characteristic impedance Z0
  and a controled voltage source that takes into consideration
  the transmission delay.
  For further details see Branin's article below.
  Resistance R' and conductance C' per meter are assumed to be zero.
  The characteristic impedance Z0 can be derived from inductance and
  capacitance per length (L' resp. C'), i. e. Z0 = sqrt(L'/C').
  The length of the line is equal to a quarter of the wavelength
  corresponding to the frequency F, i. e. the
  transmission delay is the quotient of 4 and F.
  In this case, the caracteristic impedance is called natural impedance.






References:





Branin Jr., F. H.


 Transient Analysis of Lossless Transmission Lines.
     Proceedings of the IEEE 55(1967), 2012 - 2013


 Hoefer, E. E. E.; Nielinger, H.


 SPICE : Analyseprogramm fuer elektronische
  Schaltungen. Springer-Verlag, Berlin, Heidelberg, New York, Tokyo, 1985.







Extends from Modelica.Electrical.Analog.Interfaces.TwoPort (Component with two electrical ports, including current).

Parameters




TypeNameDefaultDescription


ResistanceZ0 Natural impedance [Ohm]


FrequencyF Frequency [Hz]




Connectors




TypeNameDescription


PositivePinp1Positive pin of the left port (potential p1.v > n1.v for positive voltage drop v1)


NegativePinn1Negative pin of the left port


PositivePinp2Positive pin of the right port (potential p2.v > n2.v for positive voltage drop v2)


NegativePinn2Negative pin of the right port




Modelica definition


model TLine3 
  "Lossless transmission line with characteristic impedance Z0 and frequency F"
  extends Modelica.Electrical.Analog.Interfaces.TwoPort;
  parameter Modelica.SIunits.Resistance Z0(start=1) "Natural impedance";
  parameter Modelica.SIunits.Frequency F(start=1) "Frequency";
protected 
  Modelica.SIunits.Voltage er;
  Modelica.SIunits.Voltage es;
  Modelica.SIunits.Time TD;
equation 
  assert(Z0 > 0, "Z0 has to be positive");
  assert(F > 0, "F  has to be positive");
  TD = 1/F/4;
  i1 = (v1 - es)/Z0;
  i2 = (v2 - er)/Z0;
  es = 2*delay(v2, TD) - delay(er, TD);
  er = 2*delay(v1, TD) - delay(es, TD);
end TLine3;







Modelica.Electrical.Analog.Lines.M_OLine.segment
Modelica.Electrical.Analog.Lines.M_OLine.segment

Modelica.Electrical.Analog.Lines.M_OLine.segment

Parameters




TypeNameDefaultDescription


Integerlines3 


Integerdim_vector_lgcdiv(lines*(lines + 1), 2) 


RealCl[dim_vector_lgc]fill(1, dim_vector_lgc) 


RealRl[lines]fill(7, lines) 


RealLl[dim_vector_lgc]fill(2, dim_vector_lgc) 


RealGl[dim_vector_lgc]fill(1, dim_vector_lgc) 




Connectors




TypeNameDescription


PositivePinp[lines]Positive pin


NegativePinn[lines]Negative pin




Modelica definition


model segment

  parameter Integer lines(final min=1)=3;       //number of lines
  parameter Integer dim_vector_lgc=div(lines*(lines+1),2);
  Modelica.Electrical.Analog.Interfaces.PositivePin p[lines] "Positive pin";
  Modelica.Electrical.Analog.Interfaces.NegativePin n[lines] "Negative pin";

  parameter Real Cl[dim_vector_lgc]=fill(1,dim_vector_lgc);
  parameter Real Rl[lines]=fill(7,lines);
  parameter Real Ll[dim_vector_lgc]=fill(2,dim_vector_lgc);
  parameter Real Gl[dim_vector_lgc]= fill(1,dim_vector_lgc);

  Modelica.Electrical.Analog.Basic.Capacitor C[dim_vector_lgc](C=Cl);
  Modelica.Electrical.Analog.Basic.Resistor R[lines](R=Rl);
  Modelica.Electrical.Analog.Basic.Conductor G[dim_vector_lgc](G=Gl);
  Modelica.Electrical.Analog.Basic.M_Transformer inductance(N=lines, L=Ll);
  Modelica.Electrical.Analog.Basic.Ground M;

equation 
  for j in 1:lines-1 loop

    connect(R[j].p,p[j]);
    connect(R[j].n,inductance.p[j]);
    connect(inductance.n[j],n[j]);
    connect(inductance.n[j],C[((1+(j-1)*lines)-((j-2)*(j-1))*0.5)].p);
    connect(C[((1+(j-1)*lines)-((j-2)*(j-1))*0.5)].n,M.p);
    connect(inductance.n[j],G[((1+(j-1)*lines)-((j-2)*(j-1))*0.5)].p);
    connect(G[((1+(j-1)*lines)-((j-2)*(j-1))*0.5)].n,M.p);

    for i in j+1:lines loop
      connect(inductance.n[j],C[((1+(j-1)*lines)-((j-2)*(j-1))*0.5)+1+i-(j+1)].p);
      connect(C[((1+(j-1)*lines)-((j-2)*(j-1))*0.5)+1+i-(j+1)].n,inductance.n[i]);
      connect(inductance.n[j],G[((1+(j-1)*lines)-((j-2)*(j-1))*0.5)+1+i-(j+1)].p);
      connect(G[((1+(j-1)*lines)-((j-2)*(j-1))*0.5)+1+i-(j+1)].n,inductance.n[i]);
    end for;
  end for;
    connect(R[lines].p,p[lines]);
    connect(R[lines].n,inductance.p[lines]);
    connect(inductance.n[lines],n[lines]);
    connect(inductance.n[lines],C[dim_vector_lgc].p);
    connect(C[dim_vector_lgc].n,M.p);
    connect(inductance.n[lines],G[dim_vector_lgc].p);
    connect(G[dim_vector_lgc].n,M.p);

end segment;







Modelica.Electrical.Analog.Lines.M_OLine.segment_last
Modelica.Electrical.Analog.Lines.M_OLine.segment_last

Modelica.Electrical.Analog.Lines.M_OLine.segment_last

Parameters




TypeNameDefaultDescription


Integerlines3 


Integerdim_vector_lgcdiv(lines*(lines + 1), 2) 


RealRl[lines]fill(1, lines) 


RealLl[dim_vector_lgc]fill(1, dim_vector_lgc) 




Connectors




TypeNameDescription


PositivePinp[lines]Positive pin


NegativePinn[lines]Negative pin




Modelica definition


model segment_last

  Modelica.Electrical.Analog.Interfaces.PositivePin p[lines] "Positive pin";
  Modelica.Electrical.Analog.Interfaces.NegativePin n[lines] "Negative pin";
  parameter Integer lines(final min=1)=3;
  parameter Integer dim_vector_lgc= div(lines*(lines+1),2);
  parameter Real Rl[lines]=fill(1,lines);
  parameter Real Ll[dim_vector_lgc]=fill(1,dim_vector_lgc);
  Modelica.Electrical.Analog.Basic.Resistor R[lines](R=Rl);
  Modelica.Electrical.Analog.Basic.M_Transformer inductance(  N=lines, L=Ll);
  Modelica.Electrical.Analog.Basic.Ground M;

equation 
  for j in 1:lines-1 loop

    connect(p[j],inductance.p[j]);
    connect(inductance.n[j],R[j].p);
    connect(R[j].n,n[j]);
  end for;
    connect(p[lines],inductance.p[lines]);
    connect(inductance.n[lines],R[lines].p);
    connect(R[lines].n,n[lines]);

end segment_last;





HTML-documentation generated by Dymola Sun Jan 17 21:10:08 2010.