Buildings.Controls.OBC.Utilities.PIDWithAutotuning.AutoTuner.AMIGO.BaseClasses

Package with base classes

Information

This package contains base classes to construct blocks in Buildings.Controls.OBC.Utilities.PIDWithAutotuning.AutoTuner.AMIGO.

Package Content

Name	Description
PIDDerivativeTime	Identify the derivative time of a PID controller
PIDGain	Identify the control gain of a PID controller
PIDIntegralTime	Identify the integral time of a PID controller
PIGain	Identify the control gain of a PI controller
PIIntegralTime	Identify the integral time of a PI controller
Validation	Collection of validation models

Buildings.Controls.OBC.Utilities.PIDWithAutotuning.AutoTuner.AMIGO.BaseClasses.PIDDerivativeTime

Identify the derivative time of a PID controller

Buildings.Controls.OBC.Utilities.PIDWithAutotuning.AutoTuner.AMIGO.BaseClasses.PIDDerivativeTime

Information

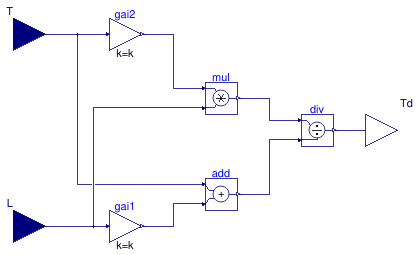
This block calculates the derivative time of a PID controller as

T_d = 0.5 L T/(0.3 L + T),

where T is the time constant of the first-order plus time-delay (FOPTD) model and L is the time delay of the FOPTD model.

References

Åström, Karl Johan and Tore Hägglund (2004) "Revisiting the Ziegler–Nichols step response method for PID control." Journal of Process Control 14.6 (2004): 635-650.

Connectors

Type	Name	Description
input RealInput	T	Time constant of a first-order plus time-delay (FOPTD) model [s]
input RealInput	L	Time delay of the FOPTD model [s]
output RealOutput	Td	Time constant signal for the derivative term [s]

Modelica definition

block PIDDerivativeTime "Identify the derivative time of a PID controller" Buildings.Controls.OBC.CDL.Interfaces.RealInput T( final quantity="Time", final unit="s", min=100*Buildings.Controls.OBC.CDL.Constants.eps) "Time constant of a first-order plus time-delay (FOPTD) model"; Buildings.Controls.OBC.CDL.Interfaces.RealInput L( final quantity="Time", final unit="s", min=100*Buildings.Controls.OBC.CDL.Constants.eps) "Time delay of the FOPTD model"; Buildings.Controls.OBC.CDL.Interfaces.RealOutput Td( final quantity="Time", final unit="s", min=100*Buildings.Controls.OBC.CDL.Constants.eps) "Time constant signal for the derivative term"; protected Buildings.Controls.OBC.CDL.Reals.MultiplyByParameter gai1( final k=0.3) "Block that calculates the product of a constant and the input"; Buildings.Controls.OBC.CDL.Reals.MultiplyByParameter gai2( final k=0.5) "Block that calculates the product of a constant and the input"; Buildings.Controls.OBC.CDL.Reals.Multiply mul "Block that calculates the product of the two inputs"; Buildings.Controls.OBC.CDL.Reals.Add add "Block that calculates the sum of the two inputs"; Buildings.Controls.OBC.CDL.Reals.Divide div "Block that calculates input 1 divided by input 2"; equation connect(div.y, Td); connect(gai1.u, L); connect(gai1.y, add.u2); connect(add.u1, T); connect(gai2.u, T); connect(mul.u2, L); connect(gai2.y, mul.u1); connect(mul.y, div.u1); connect(div.u2, add.y); end PIDDerivativeTime;

Buildings.Controls.OBC.Utilities.PIDWithAutotuning.AutoTuner.AMIGO.BaseClasses.PIDGain

Identify the control gain of a PID controller

Buildings.Controls.OBC.Utilities.PIDWithAutotuning.AutoTuner.AMIGO.BaseClasses.PIDGain

Information

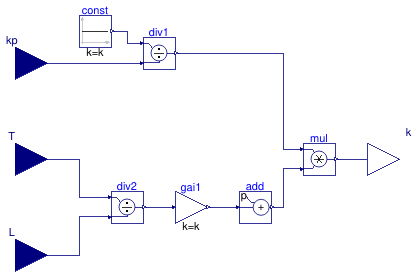
This block calculates the control gain of a PID model as

k = 1/k_p + (0.2 + 0.45 T/L),

where k_p is the gain of the first-order plus time-delay (FOPTD) model, T is the time constant of the FOPTD model, and L is the time delay of the FOPTD model.

References

Åström, Karl Johan and Tore Hägglund (2004) "Revisiting the Ziegler–Nichols step response method for PID control." Journal of Process Control 14.6 (2004): 635-650.

Connectors

Type	Name	Description
input RealInput	kp	Gain of a first-order plus time-delay (FOPTD) model
input RealInput	T	Time constant of the FOPTD model [s]
input RealInput	L	Time delay of the FOPTD model [s]
output RealOutput	k	Control gain

Modelica definition

block PIDGain "Identify the control gain of a PID controller" Buildings.Controls.OBC.CDL.Interfaces.RealInput kp( final min=1E-6) "Gain of a first-order plus time-delay (FOPTD) model"; Buildings.Controls.OBC.CDL.Interfaces.RealInput T( final quantity="Time", final unit="s", min=100*Buildings.Controls.OBC.CDL.Constants.eps) "Time constant of the FOPTD model"; Buildings.Controls.OBC.CDL.Interfaces.RealInput L( final quantity="Time", final unit="s", min=100*Buildings.Controls.OBC.CDL.Constants.eps) "Time delay of the FOPTD model"; Buildings.Controls.OBC.CDL.Interfaces.RealOutput k "Control gain"; protected Buildings.Controls.OBC.CDL.Reals.Divide div1 "Block that calculates the inverse of the input"; Buildings.Controls.OBC.CDL.Reals.Sources.Constant const( final k=1) "Constant value 1"; Buildings.Controls.OBC.CDL.Reals.AddParameter add( final p=0.2) "Block that calculates the sum of the two inputs"; Buildings.Controls.OBC.CDL.Reals.Divide div2 "Block that calculates the ratio of the time constant to the time delay"; Buildings.Controls.OBC.CDL.Reals.MultiplyByParameter gai1( final k=0.45) "Block that calculates the product of the two inputs"; Buildings.Controls.OBC.CDL.Reals.Multiply mul "Block that calculates the sum of the two inputs"; equation connect(div1.u2, kp); connect(const.y, div1.u1); connect(div2.u2, L); connect(div2.u1, T); connect(gai1.u, div2.y); connect(gai1.y, add.u); connect(mul.y, k); connect(div1.y, mul.u1); connect(mul.u2, add.y); end PIDGain;

Buildings.Controls.OBC.Utilities.PIDWithAutotuning.AutoTuner.AMIGO.BaseClasses.PIDIntegralTime

Identify the integral time of a PID controller

Buildings.Controls.OBC.Utilities.PIDWithAutotuning.AutoTuner.AMIGO.BaseClasses.PIDIntegralTime

Information

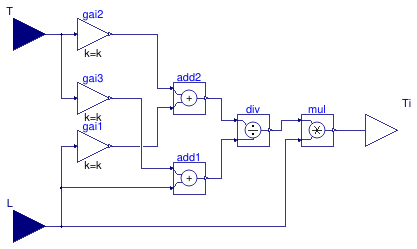
This block calculates the integral time of a PID model as

T_i = L (0.4 L + 0.8 T)/(L + 0.1 T),

where T is the time constant of the first-order plus time-delay (FOPTD) model and L is the time delay of the FOPTD model.

References

Åström, Karl Johan and Tore Hägglund (2004) "Revisiting the Ziegler–Nichols step response method for PID control." Journal of Process Control 14.6 (2004): 635-650.

Connectors

Type	Name	Description
input RealInput	T	Time constant of a first-order plus time-delay (FOPTD) model [s]
input RealInput	L	Time delay of the FOPTD model [s]
output RealOutput	Ti	Time constant signal for the integral term [s]

Modelica definition

block PIDIntegralTime "Identify the integral time of a PID controller" Buildings.Controls.OBC.CDL.Interfaces.RealInput T( final quantity="Time", final unit="s", min=100*Buildings.Controls.OBC.CDL.Constants.eps) "Time constant of a first-order plus time-delay (FOPTD) model"; Buildings.Controls.OBC.CDL.Interfaces.RealInput L( final quantity="Time", final unit="s", min=100*Buildings.Controls.OBC.CDL.Constants.eps) "Time delay of the FOPTD model"; Buildings.Controls.OBC.CDL.Interfaces.RealOutput Ti( final quantity="Time", final unit="s", min=100*Buildings.Controls.OBC.CDL.Constants.eps) "Time constant signal for the integral term"; protected Buildings.Controls.OBC.CDL.Reals.Add add1 "Block that calculates the sum of the two inputs"; Buildings.Controls.OBC.CDL.Reals.Add add2 "Block that calculates the sum of the two inputs"; Buildings.Controls.OBC.CDL.Reals.Divide div "Block that calculates input 1 divided by input 2"; Buildings.Controls.OBC.CDL.Reals.MultiplyByParameter gai1( final k=0.4) "Block that calculates the product of a constant and the input"; Buildings.Controls.OBC.CDL.Reals.MultiplyByParameter gai2( final k=0.8) "Block that calculates the product of a constant and the input"; Buildings.Controls.OBC.CDL.Reals.MultiplyByParameter gai3( final k=0.1) "Block that calculates the product of a constant and the input"; Buildings.Controls.OBC.CDL.Reals.Multiply mul "Block that calculates the two inputs"; equation connect(gai1.u, L); connect(gai3.u, T); connect(gai2.u, T); connect(gai1.y, add2.u2); connect(add2.u1, gai2.y); connect(add1.u2, L); connect(add1.u1, gai3.y); connect(div.y, mul.u1); connect(mul.u2, L); connect(mul.y, Ti); connect(div.u2, add1.y); connect(div.u1, add2.y); end PIDIntegralTime;

Buildings.Controls.OBC.Utilities.PIDWithAutotuning.AutoTuner.AMIGO.BaseClasses.PIGain

Identify the control gain of a PI controller

Buildings.Controls.OBC.Utilities.PIDWithAutotuning.AutoTuner.AMIGO.BaseClasses.PIGain

Information

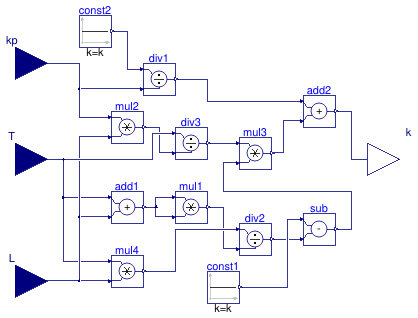
This block calculates the control gain of a PI model as

k = 0.15/k_p + (0.35-LT/(L+T)²)(T/k_p/L),

where k_p is the gain of the first-order plus time-delay (FOPTD) model, T is the time constant of the FOPTD model, and L is the time delay of the FOPTD model.

References

Garpinger, Olof, Tore Hägglund, and Karl Johan Åström (2014) "Performance and robustness trade-offs in PID control." Journal of Process Control 24.5 (2014): 568-577.

Connectors

Type	Name	Description
input RealInput	kp	Gain of a first-order plus time-delay (FOPTD) model
input RealInput	T	Time constant of the FOPTD model [s]
input RealInput	L	Time delay of the FOPTD model [s]
output RealOutput	k	Control gain

Modelica definition

block PIGain "Identify the control gain of a PI controller" Buildings.Controls.OBC.CDL.Interfaces.RealInput kp( final min=1E-6) "Gain of a first-order plus time-delay (FOPTD) model"; Buildings.Controls.OBC.CDL.Interfaces.RealInput T( final quantity="Time", final unit="s", min=100*Buildings.Controls.OBC.CDL.Constants.eps) "Time constant of the FOPTD model"; Buildings.Controls.OBC.CDL.Interfaces.RealInput L( final quantity="Time", final unit="s", min=100*Buildings.Controls.OBC.CDL.Constants.eps) "Time delay of the FOPTD model"; Buildings.Controls.OBC.CDL.Interfaces.RealOutput k "Control gain"; protected Buildings.Controls.OBC.CDL.Reals.Add add1 "Calculate the sum of the time constant and the time delay"; Buildings.Controls.OBC.CDL.Reals.Add add2 "Calculate the sum of the two inputs"; Buildings.Controls.OBC.CDL.Reals.Sources.Constant const1(final k=0.35) "Constant value"; Buildings.Controls.OBC.CDL.Reals.Sources.Constant const2(final k=0.15) "Constant value"; Buildings.Controls.OBC.CDL.Reals.Divide div1 "Block that calculates input 1 divided by input 2"; Buildings.Controls.OBC.CDL.Reals.Divide div2 "Block that calculates input 1 divided by input 2"; Buildings.Controls.OBC.CDL.Reals.Divide div3 "Block that calculates input 1 divided by input 2"; Buildings.Controls.OBC.CDL.Reals.Multiply mul1 "Block that calculates the sum of the two inputs"; Buildings.Controls.OBC.CDL.Reals.Multiply mul2 "Block that calculates the product of the two inputs"; Buildings.Controls.OBC.CDL.Reals.Multiply mul3 "Block that calculates the product of the two inputs"; Buildings.Controls.OBC.CDL.Reals.Multiply mul4 "Block that calculates the product of the two inputs"; Buildings.Controls.OBC.CDL.Reals.Subtract sub "Block that calculates the difference between the two inputs"; equation connect(div1.u2, kp); connect(add2.u1, div1.y); connect(add1.u1, T); connect(add1.u2, L); connect(mul4.u1, T); connect(mul4.u2, L); connect(mul1.u1, add1.y); connect(mul1.u2, add1.y); connect(div2.u2, mul1.y); connect(div2.u1, mul4.y); connect(mul2.u1, kp); connect(mul2.u2, L); connect(div3.u2, mul2.y); connect(div3.u1, T); connect(mul3.u1, div3.y); connect(const2.y, div1.u1); connect(add2.u2, mul3.y); connect(add2.y, k); connect(div2.y, sub.u2); connect(const1.y, sub.u1); connect(sub.y, mul3.u2); end PIGain;

Buildings.Controls.OBC.Utilities.PIDWithAutotuning.AutoTuner.AMIGO.BaseClasses.PIIntegralTime

Identify the integral time of a PI controller

Buildings.Controls.OBC.Utilities.PIDWithAutotuning.AutoTuner.AMIGO.BaseClasses.PIIntegralTime

Information

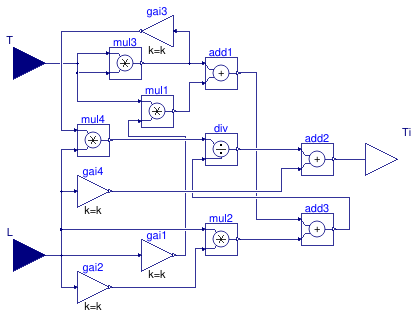
This block calculates the integral time of a PI model as

T_i = 0.35 L + 13 L T²/(T² + 12 L T + 7 L²),

where T is the time constant of the first-order plus time-delay (FOPTD) model and L is the time delay of the FOPTD model.

References

Garpinger, Olof, Tore Hägglund, and Karl Johan Åström (2014) "Performance and robustness trade-offs in PID control." Journal of Process Control 24.5 (2014): 568-577.

Connectors

Type	Name	Description
input RealInput	T	Time constant of a first-order plus time-delay (FOPTD) model [s]
input RealInput	L	Time delay of the FOPTD model [s]
output RealOutput	Ti	Time constant for the integral term [s]

Modelica definition

block PIIntegralTime "Identify the integral time of a PI controller" Buildings.Controls.OBC.CDL.Interfaces.RealInput T( final quantity="Time", final unit="s", min=100*Buildings.Controls.OBC.CDL.Constants.eps) "Time constant of a first-order plus time-delay (FOPTD) model"; Buildings.Controls.OBC.CDL.Interfaces.RealInput L( final quantity="Time", final unit="s", min=100*Buildings.Controls.OBC.CDL.Constants.eps) "Time delay of the FOPTD model"; Buildings.Controls.OBC.CDL.Interfaces.RealOutput Ti( final quantity="Time", final unit="s", min=100*Buildings.Controls.OBC.CDL.Constants.eps) "Time constant for the integral term"; protected Buildings.Controls.OBC.CDL.Reals.Add add1 "Block that calculates the sum of the two inputs"; Buildings.Controls.OBC.CDL.Reals.Add add2 "Block that calculates the sum of the two inputs"; Buildings.Controls.OBC.CDL.Reals.Add add3 "Block that calculates the sum of the two inputs"; Buildings.Controls.OBC.CDL.Reals.Divide div "Block that calculates the input 1 divided by input 2"; Buildings.Controls.OBC.CDL.Reals.MultiplyByParameter gai1( final k=12) "Block that calculates the product of a constant and the input"; Buildings.Controls.OBC.CDL.Reals.MultiplyByParameter gai2( final k=7) "Block that calculates the product of a constant and the input"; Buildings.Controls.OBC.CDL.Reals.MultiplyByParameter gai3( final k=13) "Block that calculates the product of a constant and the input"; Buildings.Controls.OBC.CDL.Reals.MultiplyByParameter gai4( final k=0.35) "Block that calculates the product of a constant and the input"; Buildings.Controls.OBC.CDL.Reals.Multiply mul1 "Block that calculates the product of the two inputs"; Buildings.Controls.OBC.CDL.Reals.Multiply mul2 "Block that calculates the product of the two inputs"; Buildings.Controls.OBC.CDL.Reals.Multiply mul3 "Block that calculates the square value of the input time constant"; Buildings.Controls.OBC.CDL.Reals.Multiply mul4 "Block that calculates the product of the two inputs"; equation connect(add2.y, Ti); connect(gai4.u, L); connect(mul3.u1, T); connect(mul3.u2, T); connect(gai1.u, L); connect(gai1.y, mul1.u2); connect(mul1.u1, T); connect(gai2.u, L); connect(gai2.y, mul2.u2); connect(mul2.u1, L); connect(gai3.u, mul3.y); connect(add1.u1, mul3.y); connect(mul1.y, add1.u2); connect(mul2.y, add3.u2); connect(add3.u1, add1.y); connect(add3.y, div.u2); connect(div.y, add2.u1); connect(add2.u2, gai4.y); connect(mul4.u2, L); connect(gai3.y, mul4.u1); connect(mul4.y, div.u1); end PIIntegralTime;