Buildings.HeatTransfer.Conduction
Package with models for heat conduction
Information
This package provides component models to compute heat conduction.
Implementation
The package declares the constant nSupPCM,
which is equal to the number of support points that are used
to approximate the specific internal energy versus temperature relation.
This approximation is used by
Buildings.HeatTransfer.Conduction.SingleLayer
to replace the piece-wise linear function by a cubic hermite spline, with
linear extrapolation, in order to avoid state events during the simulation.
Extends from Modelica.Icons.VariantsPackage (Icon for package containing variants).
Package Content
| Name | Description |
|---|---|
| Model for heat conductance through a solid with multiple material layers | |
| Model for single layer heat conductance | |
| Heat conduction in a cylinder | |
| nSupPCM=6 | Number of support points to approximate u(T) releation, used only for phase change material |
| Package with base classes for Buildings.HeatTransfer.Conduction |
Types and constants
constant Integer nSupPCM = 6 "Number of support points to approximate u(T) releation, used only for phase change material";
 Buildings.HeatTransfer.Conduction.MultiLayer
Buildings.HeatTransfer.Conduction.MultiLayer
Model for heat conductance through a solid with multiple material layers
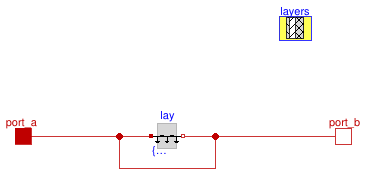
Information
This is a model of a heat conductor with multiple material layers and energy storage. The construction has at least one material layer, and each layer has at least one temperature node. The layers are modeled using an instance of Buildings.HeatTransfer.Conduction.SingleLayer. See this model for an explanation of the equations that are applied to each material layer.
Important parameters
The construction material is defined by a record of the package Buildings.HeatTransfer.Data.OpaqueConstructions. This record allows specifying materials that store energy, and material that are a thermal conductor only with no heat storage. To assign the material properties to this model, do the following:
- Create an instance of a record of Buildings.HeatTransfer.Data.OpaqueConstructions, for example by dragging the record into the schematic model editor.
-
Make sure the instance has the attribute
parameter, which may not be assigned automatically when you drop the model in a graphical editor. For example, an instanciation may look likeparameter Data.OpaqueConstructions.Insulation100Concrete200 layers "Material layers of construction" annotation (Placement(transformation(extent={{-80,60},{-60,80}}))); - Assign the instance of the material to the instance of the heat transfer model as shown in Buildings.HeatTransfer.Examples.ConductorMultiLayer.
The parameters stateAtSurface_a and
stateAtSurface_b
determine whether there is a state variable at these surfaces,
as described above.
Note that if stateAtSurface_a = true,
then there is temperature state on the surface a with prescribed
value, as determined by the differential equation of the heat conduction.
Hence, in this situation, it is not possible to
connect a temperature boundary condition such as
Buildings.HeatTransfer.Sources.FixedTemperature as this would
yield to specifying the same temperature twice.
To avoid this, either set stateAtSurface_a = false,
or place a thermal resistance
between the boundary condition and the surface of this model.
The same applies for surface b.
See the examples in
Buildings.HeatTransfer.Examples.
Extends from Buildings.HeatTransfer.Conduction.BaseClasses.PartialConductor (Partial model for heat conductor), Buildings.HeatTransfer.Conduction.BaseClasses.PartialConstruction (Partial model for multi-layer constructions).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Area | A | Heat transfer area [m2] | |
| ThermalResistance | R | sum(lay[i].R for i in 1:nLay) | Thermal resistance of construction [K/W] |
| Generic | layers | redeclare parameter Building... | Construction definition from Data.OpaqueConstructions |
| Initialization | |||
| Boolean | steadyStateInitial | false | =true initializes dT(0)/dt=0, false initializes T(0) at fixed temperature using T_a_start and T_b_start |
| Temperature | T_a_start | 293.15 | Initial temperature at port_a, used if steadyStateInitial = false [K] |
| Temperature | T_b_start | 293.15 | Initial temperature at port_b, used if steadyStateInitial = false [K] |
| Dynamics | |||
| Boolean | stateAtSurface_a | true | =true, a state will be at the surface a |
| Boolean | stateAtSurface_b | true | =true, a state will be at the surface b |
Connectors
| Type | Name | Description |
|---|---|---|
| HeatPort_a | port_a | Heat port at surface a |
| HeatPort_b | port_b | Heat port at surface b |
Modelica definition
 Buildings.HeatTransfer.Conduction.SingleLayer
Buildings.HeatTransfer.Conduction.SingleLayer
Model for single layer heat conductance

Information
This is a model of a heat conductor for a single layer of homogeneous material that computes transient or steady-state heat conduction.
Main equations
Transient heat conduction in materials without phase change
If the material is a record that extends
Buildings.HeatTransfer.Data.Solids and its
specific heat capacity (as defined by the record material.c)
is non-zero, then this model computes transient heat conduction, i.e., it
computes a numerical approximation to the solution of the heat equation
ρ c (∂ T(s,t) ⁄ ∂t) = k (∂² T(s,t) ⁄ ∂s²),
where ρ is the mass density, c is the specific heat capacity per unit mass, T is the temperature at location s and time t and k is the heat conductivity. At the locations s=0 and s=x, where x is the material thickness, the temperature and heat flow rate is equal to the temperature and heat flow rate of the heat ports.
Transient heat conduction in phase change materials
If the material is declared using a record of type
Buildings.HeatTransfer.Data.SolidsPCM, the heat transfer
in a phase change material is computed.
The record
Buildings.HeatTransfer.Data.SolidsPCM
declares the solidus temperature TSol,
the liquidus temperature TLiq and the latent heat of
phase transformation LHea.
For heat transfer with phase change, the specific internal energy u
is the dependent variable, rather than the temperature.
Therefore, the governing equation is
ρ (∂ u(s,t) ⁄ ∂t) = k (∂² T(s,t) ⁄ ∂s²).
The constitutive relation between specific internal energy u and temperature T is defined in Buildings.HeatTransfer.Conduction.BaseClasses.temperature_u by using cubic hermite spline interpolation with linear extrapolation.
Steady-state heat conduction
If material.c=0, or if the material extends
Buildings.HeatTransfer.Data.Resistances,
then steady-state heat conduction is computed. In this situation, the heat
flow between its heat ports is
Q = A k ⁄ x (Ta-Tb),
where A is the cross sectional area, x is the layer thickness, Ta is the temperature at port a and Tb is the temperature at port b.
Spatial discretization
To spatially discretize the heat equation, the construction is
divided into compartments (control volumes) with material.nSta ≥ 1 state variables.
Each control volume has the same material properties.
The state variables are connected to each other through thermal resistances.
If stateAtSurface_a = true, a state is placed
at the surface a, and similarly, if
stateAtSurface_b = true, a state is placed
at the surface b.
Otherwise, these states are placed inside the material, away
from the surface.
Thus, to obtain
the surface temperature, use port_a.T (or port_b.T)
and not the variable T[1].
x
and a discretization with four state variables.
-
If
stateAtSurface_a = falseandstateAtSurface_b = false, then each of the four state variables is placed in the middle of a control volume with lengthl=x/material.nSta. -
If
stateAtSurface_a = trueorstateAtSurface_b = true, then one state is placed on the surface of the material. Each of the remaining three states is placed in the middle of a control volume with lengthl=x/(material.nSta-1). -
If
stateAtSurface_a = trueandstateAtSurface_b = true, then two states are placed on the surfaces of the material. Each of the remaining two states is placed in the middle of a control volume with lengthl=x/(material.nSta-2).
To build multi-layer constructions, use Buildings.HeatTransfer.Conduction.MultiLayer instead of this model.
Important parameters
The parameters stateAtSurface_a and
stateAtSurface_b
determine whether there is a state variable at these surfaces,
as described above.
Note that if stateAtSurface_a = true,
then there is temperature state on the surface a with prescribed
value, as determined by the differential equation of the heat conduction.
Hence, in this situation, it is not possible to
connect a temperature boundary condition such as
Buildings.HeatTransfer.Sources.FixedTemperature as this would
yield to specifying the same temperature twice.
To avoid this, either set stateAtSurface_a = false,
or place a thermal resistance
between the boundary condition and the surface of this model.
The same applies for surface b.
See the examples in
Buildings.HeatTransfer.Examples.
Extends from Buildings.HeatTransfer.Conduction.BaseClasses.PartialConductor (Partial model for heat conductor).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Area | A | Heat transfer area [m2] | |
| ThermalResistance | R | if (material.R < Modelica.Co... | Thermal resistance of construction [K/W] |
| Material | material | redeclare parameter Data.Bas... | Material from Data.Solids, Data.SolidsPCM or Data.Resistances |
| Initialization | |||
| Boolean | steadyStateInitial | false | =true initializes dT(0)/dt=0, false initializes T(0) at fixed temperature using T_a_start and T_b_start |
| Temperature | T_a_start | 293.15 | Initial temperature at port_a, used if steadyStateInitial = false [K] |
| Temperature | T_b_start | 293.15 | Initial temperature at port_b, used if steadyStateInitial = false [K] |
| Dynamics | |||
| Boolean | stateAtSurface_a | true | =true, a state will be at the surface a |
| Boolean | stateAtSurface_b | true | =true, a state will be at the surface b |
| Advanced | |||
| Integer | nSta2 | material.nSta | Number of states in a material (do not overwrite, used to work around Dymola 2017 bug) |
Connectors
| Type | Name | Description |
|---|---|---|
| HeatPort_a | port_a | Heat port at surface a |
| HeatPort_b | port_b | Heat port at surface b |
Modelica definition
 Buildings.HeatTransfer.Conduction.SingleLayerCylinder
Buildings.HeatTransfer.Conduction.SingleLayerCylinder
Heat conduction in a cylinder

Information
Model for radial heat transfer in a hollow cylinder.If the heat capacity of the material is non-zero, then this model computes transient heat conduction, i.e., it computes a numerical approximation to the solution of the heat equation
ρ c ( ∂ T(r,t) ⁄ ∂t ) = k ( ∂² T(r,t) ⁄ ∂r² + 1 ⁄ r ∂ T(r,t) ⁄ ∂r ),
where ρ is the mass density, c is the specific heat capacity per unit mass, T is the temperature at location r and time t and k is the heat conductivity. At the locations r=ra and r=rb, the temperature and heat flow rate are equal to the temperature and heat flow rate of the heat ports.
If the heat capacity of the material is set to zero, then steady-state heat flow is computed using
Q = 2 π k (Ta-Tb)⁄ ln(ra ⁄ rb),
where ra is the internal radius, rb is the external radius, Ta is the temperature at port a and Tb is the temperature at port b.
Implementation
To spatially discretize the heat equation, the construction is
divided into compartments with material.nSta ≥ 1 state variables.
The state variables are connected to each other through thermal conductors.
There is also a thermal conductor
between the surfaces and the outermost state variables. Thus, to obtain
the surface temperature, use port_a.T (or port_b.T)
and not the variable T[1].
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Generic | material | redeclare parameter Building... | Material thermal properties |
| Height | h | Height of the cylinder [m] | |
| Radius | r_a | Internal radius [m] | |
| Radius | r_b | External radius [m] | |
| Integer | nSta | Number of state variables | |
| Real | griFac | 2 | Grid factor for spacing |
| Initialization | |||
| Temperature | TInt_start | 293.15 | Initial temperature at port_a, used if steadyStateInitial = false [K] |
| Temperature | TExt_start | 293.15 | Initial temperature at port_b, used if steadyStateInitial = false [K] |
| Boolean | steadyStateInitial | false | true initializes dT(0)/dt=0, false initializes T(0) at fixed temperature using T_a_start and T_b_start |
Connectors
| Type | Name | Description |
|---|---|---|
| HeatPort_a | port_a | Heat port at surface a |
| HeatPort_b | port_b | Heat port at surface b |



