Buildings.Fluid.Examples.Performance
Package of examples that demonstrate computation speed performance
Information
This package contains examples that illustrate the Modelica conference paper by Jorissen et al. (2015) about speed optimization.
References
-
Filip Jorissen, Michael Wetter and Lieve Helsen.
Simulation speed analysis and improvements of Modelica models for building energy simulation.
Submitted: 11th Modelica Conference. Paris, France. Sep. 2015.
Extends from Modelica.Icons.ExamplesPackage (Icon for packages containing runnable examples).
Package Content
| Name | Description |
|---|---|
| Example 1 model without mixing volume | |
| Example 1 model with mixing volume | |
| Example 2 model with series pressure components | |
| Example 3 model with mixed series/parallel pressure drop components | |
| Example 4 model of simple condensing heat exchanger | |
| Example 5 model of Modelica code that is inefficiently compiled into C-code | |
| Example 6 model of Modelica code that is inefficiently compiled into C-code | |
| Example 7 model of Modelica code that is more efficiently compiled into C-code | |
| Common subexpression elimination example | |
| Package with various configurations of pressure drop models to analyze symbolic processing | |
 Buildings.Fluid.Examples.Performance.Example1v1
Buildings.Fluid.Examples.Performance.Example1v1
Example 1 model without mixing volume
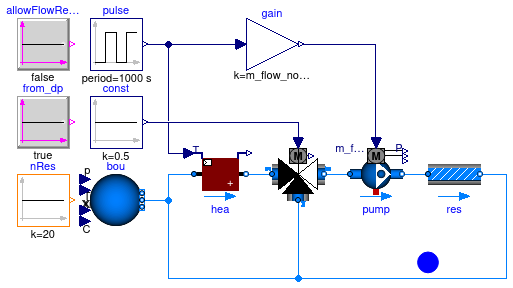
Information
This model demonstrates the impact of the allowFlowReversal
and from_dp parameters on the sizes of nonlinear algebraic loops.
The user can change the parameter value in the respective
BooleanConstant blocks and rerun the simulation to compare the performance.
The results are also demonstrated below for nRes.k = 20,
the number of parallel branches, which contain one pressure drop element each.
These results were generated using Dymola 2015FD01 64 bit on Ubuntu 14.04.
Default case:
AllowFlowReversal = true and from_dp = false
Sizes of nonlinear systems of equations: {6, 21, 46}
Sizes after manipulation of the nonlinear systems: {1, 19, 22}
Change 1:
AllowFlowReversal = false and from_dp = false
Sizes of nonlinear systems of equations: {6, 21}
Sizes after manipulation of the nonlinear systems: {1, 19}
Change 2:
AllowFlowReversal = false and from_dp = true
Sizes of nonlinear systems of equations: {6, 21}
Sizes after manipulation of the nonlinear systems: {1, 1}
These changes also have a significant impact on the computational speed.
Following script can be used in Dymola to compare the CPU times. For this script to work, make sure that Dymola stores at least 4 results.
cpuOld=OutputCPUtime;
evaluateOld=Evaluate;
OutputCPUtime:=true;
simulateModel("Buildings.Fluid.Examples.Performance.Example1v1(allowFlowReversal.k=true, from_dp.k=false)", stopTime=10000, numberOfIntervals=10, method="dassl", resultFile="Example1v1");
simulateModel("Buildings.Fluid.Examples.Performance.Example1v2(from_dp.k=true, allowFlowReversal.k=true)", stopTime=10000, numberOfIntervals=10, method="dassl", resultFile="Example1v2");
simulateModel("Buildings.Fluid.Examples.Performance.Example1v1(allowFlowReversal.k=false, from_dp.k=false)", stopTime=10000, numberOfIntervals=10, method="dassl", resultFile="Example1v1");
simulateModel("Buildings.Fluid.Examples.Performance.Example1v1(allowFlowReversal.k=false, from_dp.k=true)", stopTime=10000, numberOfIntervals=10, method="dassl", resultFile="Example1v1");
createPlot(id=1, position={15, 10, 592, 421}, range={0.0, 10000.0, -0.01, 0.35}, autoscale=false, grid=true);
plotExpression(apply(Example1v1[end-2].CPUtime), false, "Default case", 1);
plotExpression(apply(Example1v2[end].CPUtime), false, "Adding dummy states", 1);
plotExpression(apply(Example1v1[end-1].CPUtime), false, "allowFlowReversal=false", 1);
plotExpression(apply(Example1v1[end].CPUtime), false, "allowFlowReversal=false, from_dp=true", 1);
OutputCPUtime=cpuOld;
Evaluate=evaluateOld;
See Jorissen et al. (2015) for a discussion.
References
-
Filip Jorissen, Michael Wetter and Lieve Helsen.
Simulation speed analysis and improvements of Modelica models for building energy simulation.
Submitted: 11th Modelica Conference. Paris, France. Sep. 2015.
Extends from Buildings.Fluid.Examples.Performance.BaseClasses.Example1 (Example 1 partial model).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | m_flow_nominal | 0.1 | Gain value multiplied with input signal |
Modelica definition
 Buildings.Fluid.Examples.Performance.Example1v2
Buildings.Fluid.Examples.Performance.Example1v2
Example 1 model with mixing volume
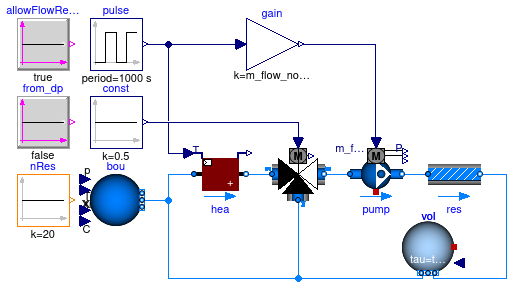
Information
This example is an extension of Buildings.Fluid.Examples.Performance.Example1v1 and demonstrates the use of mixing volumes for decoupling the algebraic loop that solves for the enthalpy of the system.
Example1v1:
Sizes of nonlinear systems of equations: {6, 21, 46}
Sizes after manipulation of the nonlinear systems: {1, 19, 22}
Example1v2 using mixing volumes:
Sizes of nonlinear systems of equations: {6, 21, 4}
Sizes after manipulation of the nonlinear systems: {1, 19, 1}
See Jorissen et al. (2015) for a discussion.
References
-
Filip Jorissen, Michael Wetter and Lieve Helsen.
Simulation speed analysis and improvements of Modelica models for building energy simulation.
Submitted: 11th Modelica Conference. Paris, France. Sep. 2015.
Extends from Buildings.Fluid.Examples.Performance.BaseClasses.Example1 (Example 1 partial model).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | m_flow_nominal | 0.1 | Gain value multiplied with input signal |
| Time | tau | 10 | Time constant at nominal flow [s] |
Modelica definition
 Buildings.Fluid.Examples.Performance.Example2
Buildings.Fluid.Examples.Performance.Example2
Example 2 model with series pressure components
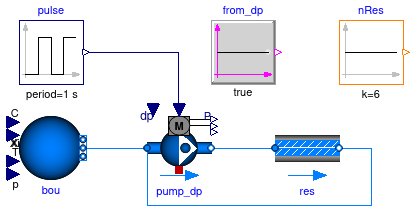
Information
This example demonstrates that the use of the parameter from_dp
can be important for reducing the size of algebraic loops in hydraulic
circuits with many pressure drop components connected in series and
a pump setting the pressure head.
If from_dp=true, we obtain:
Sizes of nonlinear systems of equations: {7}
Sizes after manipulation of the nonlinear systems: {5}
If from_dp=false, we obtain:
Sizes of nonlinear systems of equations: {7}
Sizes after manipulation of the nonlinear systems: {1}
This can have a large impact on computational speed.
Following script can be used in Dymola to compare the CPU times.
cpuOld=OutputCPUtime;
evaluateOld=Evaluate;
OutputCPUtime:=true;
simulateModel("Buildings.Fluid.Examples.Performance.Example2(from_dp.k=false)", stopTime=10000, numberOfIntervals=10, method="dassl", resultFile="Example2");
simulateModel("Buildings.Fluid.Examples.Performance.Example2(from_dp.k=true)", stopTime=10000, numberOfIntervals=10, method="dassl", resultFile="Example2");
createPlot(id=1, position={15, 10, 592, 421}, range={0.0, 10000.0, -0.01, 25}, autoscale=false, grid=true);
plotExpression(apply(Example2[end-1].CPUtime), false, "from_dp=false", 1);
plotExpression(apply(Example2[end].CPUtime), false, "from_dp=true", 1);
OutputCPUtime=cpuOld;
Evaluate=evaluateOld;
See Jorissen et al. (2015) for a discussion.
References
-
Filip Jorissen, Michael Wetter and Lieve Helsen.
Simulation speed analysis and improvements of Modelica models for building energy simulation.
Submitted: 11th Modelica Conference. Paris, France. Sep. 2015.
Extends from Modelica.Icons.Example (Icon for runnable examples).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| MassFlowRate | m_flow_nominal | 1 | Nominal mass flow rate [kg/s] |
| PressureDifference | dp_nominal | 1 | Pressure drop at nominal mass flow rate [Pa] |
Modelica definition
 Buildings.Fluid.Examples.Performance.Example3
Buildings.Fluid.Examples.Performance.Example3
Example 3 model with mixed series/parallel pressure drop components
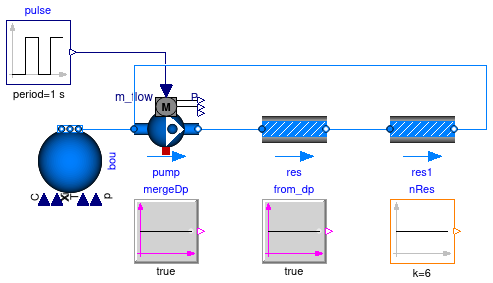
Information
This example demonstrates the importance of merging
pressure drop components that are connected in series,
into one pressure drop component.
Parameter mergeDp.k can be used to merge two components
that are connected in series.
Parameter from_dp also has an influence of the computational speed.
Following script can be used in Dymola to compare the CPU times. For this script to work, make sure that Dymola stores at least 4 results.
cpuOld=OutputCPUtime;
evaluateOld=Evaluate;
OutputCPUtime:=true;
simulateModel("Buildings.Fluid.Examples.Performance.Example3(from_dp.k=false, mergeDp.k=false, nRes.k=10)", stopTime=1000, numberOfIntervals=10, method="dassl", resultFile="Example3");
simulateModel("Buildings.Fluid.Examples.Performance.Example3(from_dp.k=false, mergeDp.k=true, nRes.k=10)", stopTime=1000, numberOfIntervals=10, method="dassl", resultFile="Example3");
simulateModel("Buildings.Fluid.Examples.Performance.Example3(from_dp.k=true, mergeDp.k=false, nRes.k=10)", stopTime=1000, numberOfIntervals=10, method="dassl", resultFile="Example3");
simulateModel("Buildings.Fluid.Examples.Performance.Example3(from_dp.k=true, mergeDp.k=true, nRes.k=10)", stopTime=1000, numberOfIntervals=10, method="dassl", resultFile="Example3");
createPlot(id=1, position={15, 10, 592, 421}, range={0.0, 1000.0, -0.01, 8}, autoscale=false, grid=true);
plotExpression(apply(Example3[end-3].CPUtime), false, "from_dp=false, mergeDp=false", 1);
plotExpression(apply(Example3[end-2].CPUtime), false, "from_dp=false, mergeDp=true", 1);
plotExpression(apply(Example3[end-1].CPUtime), false, "from_dp=true, mergeDp=false", 1);
plotExpression(apply(Example3[end].CPUtime), false, "from_dp=true, mergeDp=true", 1);
OutputCPUtime=cpuOld;
Evaluate=evaluateOld;
See Jorissen et al. (2015) for a discussion.
References
-
Filip Jorissen, Michael Wetter and Lieve Helsen.
Simulation speed analysis and improvements of Modelica models for building energy simulation.
Submitted: 11th Modelica Conference. Paris, France. Sep. 2015.
Extends from Modelica.Icons.Example (Icon for runnable examples).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| MassFlowRate | m_flow_nominal | 1 | Nominal mass flow rate [kg/s] |
| PressureDifference | dp_nominal | 1 | Pressure drop at nominal mass flow rate [Pa] |
Modelica definition
 Buildings.Fluid.Examples.Performance.Example4
Buildings.Fluid.Examples.Performance.Example4
Example 4 model of simple condensing heat exchanger
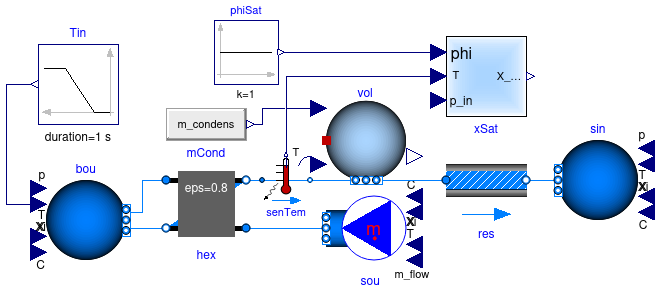
Information
This example generates a non-linear algebraic loop that consists of 12 equations before manipulation. This loop can be decoupled and removed by changing the equation
port_a.m_flow + port_b.m_flow = -mWat_flow;
in Buildings.Fluid.Interfaces.StaticTwoPortConservationEquation to
port_a.m_flow + port_b.m_flow = 0;
See Jorissen et al. (2015) for a discussion.
References
-
Filip Jorissen, Michael Wetter and Lieve Helsen.
Simulation speed analysis and improvements of Modelica models for building energy simulation.
Submitted: 11th Modelica Conference. Paris, France. Sep. 2015.
Extends from Modelica.Icons.Example (Icon for runnable examples).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Boolean | allowFlowReversal | false | = false to simplify equations, assuming, but not enforcing, no flow reversal |
Modelica definition
 Buildings.Fluid.Examples.Performance.Example5
Buildings.Fluid.Examples.Performance.Example5
Example 5 model of Modelica code that is inefficiently compiled into C-code

Information
This example illustrates the impact of Modelica code formulations on the C-code.
Compare the C-code in dsmodel.c when setting the parameter
efficient to true or false
and when adding annotation(Evaluate=true) to the parameter efficient.
This produces:
Efficient = false and Evaluate = false
helpvar[0] = sin(Time); F_[0] = helpvar[0]*(IF DP_[0] THEN W_[0] ELSE DP_[1]+DP_[2]+DP_[3]);
Efficient = false and Evaluate = true
helpvar[0] = sin(Time); F_[0] = helpvar[0]*(DP_[0]+DP_[1]+DP_[2]);
Efficient = true and Evaluate = true
helpvar[0] = sin(Time); F_[0] = helpvar[0]*W_[1];
The last option requires much less operations to be performed and is therefore more efficient.
See Jorissen et al. (2015) for a discussion.
References
-
Filip Jorissen, Michael Wetter and Lieve Helsen.
Simulation speed analysis and improvements of Modelica models for building energy simulation.
Submitted: 11th Modelica Conference. Paris, France. Sep. 2015.
Extends from Modelica.Icons.Example (Icon for runnable examples).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Boolean | efficient | false | |
| Real | a[3] | 1:3 | |
| Real | b | sum(a) |
Modelica definition
 Buildings.Fluid.Examples.Performance.Example6
Buildings.Fluid.Examples.Performance.Example6
Example 6 model of Modelica code that is inefficiently compiled into C-code

Information
This example, together with Buildings.Fluid.Examples.Performance.Example7, illustrates the overhead generated by divisions by parameters. See Jorissen et al. (2015) for a complementary discussion.
Running the following commands allows comparing the CPU times of the two models, disregarding as much as possible the influence of the integrator:
simulateModel("Buildings.Fluid.Examples.PerformanceExamples.Example6", stopTime=100, numberOfIntervals=1, method="Rkfix4", fixedstepsize=0.001, resultFile="Example6");
simulateModel("Buildings.Fluid.Examples.PerformanceExamples.Example7", stopTime=100, numberOfIntervals=1, method="Rkfix4", fixedstepsize=0.001, resultFile="Example7");
Comparing the CPU times indicates a speed improvement of 56%.
This difference almost disappears when adding annotation(Evaluate=true)
to R and C.
In dsmodel.c we find:
DynamicsSection W_[2] = divmacro(X_[0]-X_[1],"T[1]-T[2]",DP_[0],"R"); F_[0] = divmacro(W_[1]-W_[2],"Q_flow[1]-Q_flow[2]",DP_[1],"C");
This suggests that the parameter division needs to be handled during each function evaluation, probably causing the increased overhead.
The following command allows comparing the CPU times objectively.
simulateModel("Buildings.Fluid.Examples.Performance.Example6", stopTime=100, numberOfIntervals=1, method="Euler", fixedstepsize=0.001, resultFile="Example6");
See Jorissen et al. (2015) for a discussion.
References
-
Filip Jorissen, Michael Wetter and Lieve Helsen.
Simulation speed analysis and improvements of Modelica models for building energy simulation.
Submitted: 11th Modelica Conference. Paris, France. Sep. 2015.
Extends from Modelica.Icons.Example (Icon for runnable examples).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Integer | nCapacitors | 500 | |
| Real | R | 0.001 | |
| Real | C | 1000 |
Modelica definition
 Buildings.Fluid.Examples.Performance.Example7
Buildings.Fluid.Examples.Performance.Example7
Example 7 model of Modelica code that is more efficiently compiled into C-code

Information
See Buildings.Fluid.Examples.Performance.Example6 for the documentation.
Extends from Modelica.Icons.Example (Icon for runnable examples).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Integer | nTem | 500 | |
| Real | R | 0.001 | |
| Real | C | 1000 | |
| Real | tauInv | 1/(R*C) |
Modelica definition
 Buildings.Fluid.Examples.Performance.Example8
Buildings.Fluid.Examples.Performance.Example8
Common subexpression elimination example

Information
This is a very simple example demonstrating common subexpression elimination.
The Dymola generated C-code of this model is:
W_[0] = sin(Time+1); W_[1] = W_[0];
Hence, the sine and addition are evaluated once only, which is more efficient.
Extends from Modelica.Icons.Example (Icon for runnable examples).
