Buildings.Experimental.DHC.Loads

Models for computing thermal loads served by the DES

Information

This package contains models for the thermal and domestic hot water demand prediction in buildings.

Extends from Modelica.Icons.VariantsPackage (Icon for package containing variants).

Package Content

Name	Description
FlowDistribution	Model of a building hydraulic distribution system
SimpleRoomODE	Simplified model for assessing room air temperature variations around a set point
Controls	Package of control sequences for DHC systems
Types	Package with type definitions
Examples	Example models integrating multiple components
Validation	Collection of validation models
BaseClasses	Package with base classes

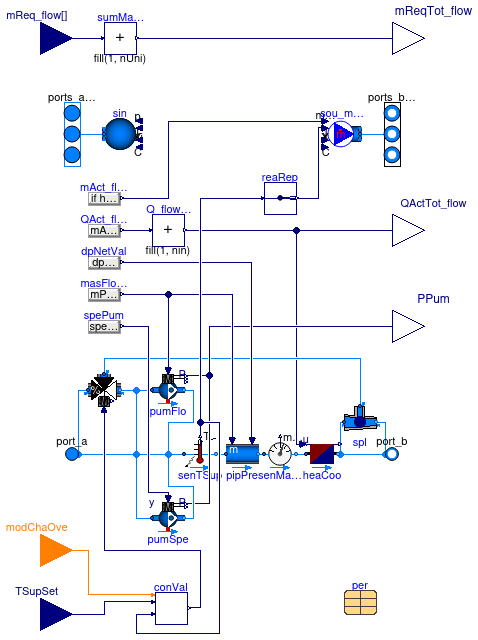
Buildings.Experimental.DHC.Loads.FlowDistribution

Model of a building hydraulic distribution system

Buildings.Experimental.DHC.Loads.FlowDistribution

Information

This model represents a two-pipe hydraulic distribution system serving multiple terminal units. It is primarily intended to be used in conjunction with models that extend Buildings.Experimental.DHC.Loads.BaseClasses.PartialTerminalUnit. The typical model structure for a whole building connected to an energy transfer station (or a dedicated plant) is illustrated in the schematics in the info section of Buildings.Experimental.DHC.Loads.BaseClasses.PartialBuilding.

The pipe network modeling is decoupled between a main distribution loop and several terminal branch circuits:

The mass flow rate in each branch circuit is equal to the mass flow rate demand yielded by the terminal unit model, constrained by the condition that the sum of all demands is lower or equal to the flow rate in the main loop. Additionally if the total flow rate demand exceeds the nominal mass flow rate the model generates an error.
The inlet temperature in each branch circuit is equal to the supply temperature in the main loop. The outlet temperature in the main loop results from transferring the enthalpy flow rate of each individual fluid stream to the main fluid stream.
The pressure drop in the main distribution loop corresponds to the pressure drop over the whole distribution system (the pump head). It is governed by an equation representing the control logic of the distribution pump.

Optionally:

A distribution pump can be modeled with a prescribed flow rate corresponding to the total flow rate demand.
A mixing valve can be modeled (together with a distribution pump) with a control loop tracking the supply temperature. Note that the nominal pressure drop of the valve is not an exposed parameter: it is set by default to 10% of the nominal total pressure drop.

Implementation

The modeling approach aims to minimize the number of algebraic equations by avoiding an explicit modeling of the terminal actuators and the whole flow network. In addition, the assumption allowFlowReversal=false is used systematically together with boundary conditions which actually ensure that no reverse flow conditions are encountered in simulation. This allows directly accessing the inlet enthalpy value of a component from the fluid port port_a with the built-in function inStream. This approach is preferred to the use of two-port sensors which introduce a state to ensure a smooth transition at flow reversal. All connected components must meet the same requirements. The impact on the computational performance is illustrated below.

Pump head computation

The pump head is computed as follows (see also Buildings.Experimental.DHC.Loads.Validation.FlowDistributionPumpControl for a comparison with an explicit modeling of the piping network).

In case of a constant pump head,
dpPum = dp_nominal.
In case of a constant flow rate (three-way valves) the network flow characteristics is considered independent from the actuator positions. Hence,
dpPum = dp_nominal.
In case of a linear head,
dpPum = dpMin + (dp_nominal - dpMin) * m_flow / m_flow_nominal.
In case of a constant speed, the pump head is computed based on the pump pressure curve and the total required mass flow rate.
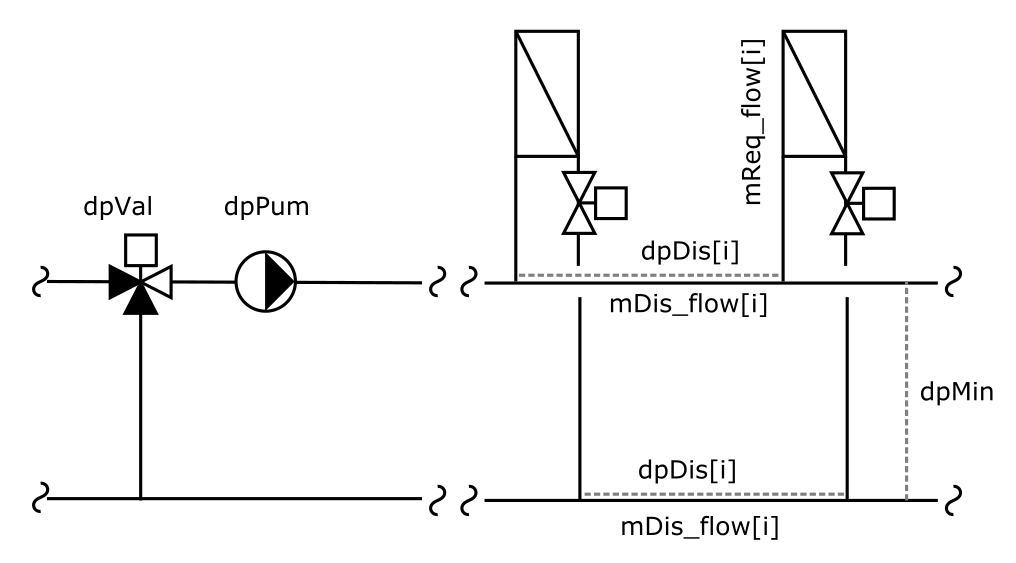
In case of a constant pressure difference at a given location, the pump head is computed according to the schematics hereunder, under the assumption of a two-pipe distribution system,
dpPum = dpMin + dpVal + 2 * Σ_i dpDis[i],

where
- dpMin is the differential pressure set point.
- dpVal is the pressure drop across the optional mixing valve. It is considered independent from the valve position, i.e., dpVal = dpVal_nominal,
- dpDis[i] is the pressure drop in the supply pipe segment directly upstream the i^th connection,
  dpDis[i] = 1 / K[i]² * mDis_flow[i] ²,
  
  where mDis_flow[i] = Σ_{i to nUni} mReq_flow[i] is the mass flow rate in the same pipe segment, and K[i] = (Σ_{i to nUni} mUni_flow_nominal[i]) / dpDis_nominal[i]^0.5 is the corresponding flow coefficient (constant).
The pressure drop in the corresponding pipe segment of the return line is considered equal, hence the factor of 2 in the above equation.

The default value for dpDis_nominal corresponds to a configuration where the differential pressure sensor is located before the most remote connected unit, 20% of the nominal pressure drop in the distribution network occurs between the pump and the first connected unit (supply and return), the remaining pressure drop is evenly distributed over each pipe segment between the other connected units. The user can override these default values with the requirement that the nominal pressure drop of each pipe segment downstream of the differential pressure sensor must be set to zero.

Energy and mass dynamics

The energy dynamics and the time constant used in the ideal heater and cooler model are exposed as advanced parameters. They are used to represent the typical dynamics over the whole piping network, from supply to return. The mass dynamics are by default identical to the energy dynamics.

Simplifying assumptions are used otherwise, namely

the pump is modeled in steady-state, and
the valve and the flow splitter are modeled with fixed initial conditions. This is because the temperature of the fluid leaving the valve is used as a control input signal. If a steady-state model is used, that temperature is computed by assuming ideal mixing at the inner fluid ports of the valve. In case of zero flow rate, the temperature value results from regularizing the corresponding equation that is not well defined in that domain. That triggers non-physical temperature variations which themselves lead to control transients when the flow rate gets reestablished. Those effects turn out to be detrimental to computational performance.

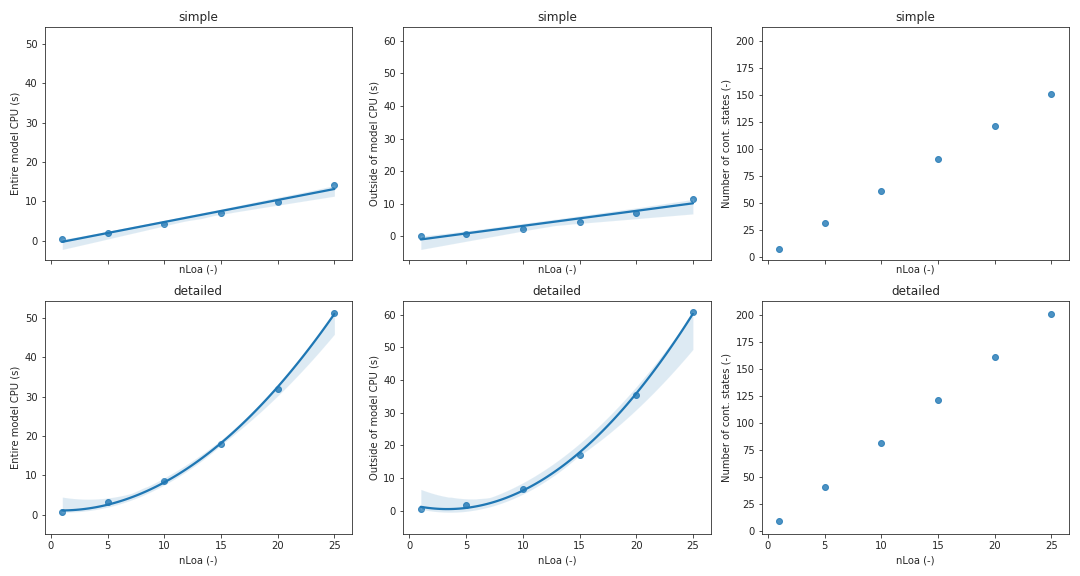
Computational performance

The figure below compares the computational performance of this model (labelled simple, see model Buildings.Experimental.DHC.Loads.Validation.BenchmarkFlowDistribution1) with an explicit modeling of the distribution network and the terminal unit actuators (labelled detailed, see model Buildings.Experimental.DHC.Loads.Validation.BenchmarkFlowDistribution2). The models are simulated with the solver CVODE from Sundials. The impact of a varying number of connected loads, nLoa, is assessed on

the total time for all model evaluations,
the total time spent between model evaluations, and
the number of continuous state variables.

A linear, resp. quadratic, regression line and the corresponding confidence interval are also plotted for the model labelled simple, resp. detailed.

Extends from Buildings.Fluid.Interfaces.PartialTwoPortInterface (Partial model transporting fluid between two ports without storing mass or energy).

Parameters

Type	Name	Default	Description
replaceable package Medium		PartialMedium	Medium in the component
Generic	per	per(pressure(V_flow=m_flow_n...	Record with performance data
Boolean	have_pum	false	Set to true if the system has a pump
Boolean	have_val	false	Set to true if the system has a mixing valve
DistributionType	typDis	Type_dis.HeatingWater	Type of distribution system
PumpControlType	typCtr	Type_ctr.ConstantHead	Type of distribution pump control
PressureDifference	dpMin	dp_nominal/2	Pressure difference set point for ConstantDp or at zero flow for LinearHead [Pa]
Nominal condition
MassFlowRate	m_flow_nominal		Nominal mass flow rate [kg/s]
Real	spePum_nominal	1	Pump speed at nominal conditions [1]
PressureDifference	dp_nominal		Pressure drop at nominal conditions [Pa]
PressureDifference	dpDis_nominal[:]	if nUni == 1 then {1/2*(dp_n...	Pressure drop between each connected unit at nominal conditions (supply line): use zero for each connection downstream the differential pressure sensor [Pa]
MassFlowRate	mUni_flow_nominal[:]	fill(m_flow_nominal/nUni, nU...	Mass flow rate of each connected unit at nominal conditions [kg/s]
Assumptions
Boolean	allowFlowReversal	false	= false to simplify equations, assuming, but not enforcing, no flow reversal
Advanced
MassFlowRate	m_flow_small	1E-4*abs(m_flow_nominal)	Small mass flow rate for regularization of zero flow [kg/s]
Diagnostics
Boolean	show_T	false	= true, if actual temperature at port is computed
Dynamics
Equations
Dynamics	energyDynamics	Modelica.Fluid.Types.Dynamic...	Type of energy balance (except for the pump always modeled in steady state)
Nominal condition
Time	tau	120	Time constant of fluid temperature variation at nominal flow rate [s]

Connectors

Type	Name	Description
replaceable package Medium		Medium in the component
FluidPort_a	port_a	Fluid connector a (positive design flow direction is from port_a to port_b)
FluidPort_b	port_b	Fluid connector b (positive design flow direction is from port_a to port_b)
FluidPorts_a	ports_a1[nPorts_a1]	Terminal units return ports
FluidPorts_b	ports_b1[nPorts_b1]	Terminal units supply ports
input RealInput	mReq_flow[nUni]	Heating or chilled water flow rate required to meet the load
input IntegerInput	modChaOve	Operating mode in change-over (1 for heating, 2 for cooling)
input RealInput	TSupSet	Supply temperature set point [K]
output RealOutput	mReqTot_flow	Total heating or chilled water flow rate required to meet the loads [kg/s]
output RealOutput	QActTot_flow	Total heat flow rate transferred to the loads (>=0 for heating) [W]
output RealOutput	PPum	Power drawn by pump motor [W]

Modelica definition

model FlowDistribution "Model of a building hydraulic distribution system" extends Buildings.Fluid.Interfaces.PartialTwoPortInterface( redeclare replaceable package Medium=Buildings.Media.Water, allowFlowReversal=false); import Type_dis=Buildings.Experimental.DHC.Loads.Types.DistributionType "Types of distribution system"; import Type_ctr=Buildings.Experimental.DHC.Loads.Types.PumpControlType "Types of distribution pump control"; replaceable parameter Buildings.Fluid.Movers.Data.Generic per( pressure( V_flow=m_flow_nominal/rho_default .* {0,1,2}, dp=dp_nominal .* {1.5,1,0.5}), motorCooledByFluid=false) constrainedby Buildings.Fluid.Movers.Data.Generic "Record with performance data"; parameter Integer nPorts_a1=0 "Number of terminal units return ports"; parameter Integer nPorts_b1=0 "Number of terminal units supply ports"; final parameter Integer nUni=nPorts_a1 "Number of served units"; parameter Boolean have_pum=false "Set to true if the system has a pump"; parameter Boolean have_val=false "Set to true if the system has a mixing valve"; parameter Type_dis typDis=Type_dis.HeatingWater "Type of distribution system"; parameter Type_ctr typCtr=Type_ctr.ConstantHead "Type of distribution pump control"; parameter Real spePum_nominal( final unit="1", final min=0, final max=1)=1 "Pump speed at nominal conditions"; parameter Modelica.SIunits.PressureDifference dp_nominal( final min=0, displayUnit="Pa") "Pressure drop at nominal conditions"; final parameter Modelica.SIunits.PressureDifference dpVal_nominal( final min=0, displayUnit="Pa")= if have_val then 0.1*dp_nominal else 0 "Mixing valve pressure drop at nominal conditions"; parameter Modelica.SIunits.PressureDifference dpDis_nominal[:]( each final min=0, each displayUnit="Pa")= if nUni == 1 then {1/2*(dp_nominal-dpVal_nominal-dpMin)} else 1/2 .* cat( 1, {(dp_nominal-dpVal_nominal-dpMin)*0.2}, fill( (dp_nominal-dpVal_nominal-dpMin)*0.8/(nUni-1), nUni-1)) "Pressure drop between each connected unit at nominal conditions (supply line): use zero for each connection downstream the differential pressure sensor"; parameter Modelica.SIunits.PressureDifference dpMin( final min=0, displayUnit="Pa")=dp_nominal/2 "Pressure difference set point for ConstantDp or at zero flow for LinearHead"; parameter Modelica.SIunits.MassFlowRate mUni_flow_nominal[:]( each final min=0)=fill( m_flow_nominal/nUni, nUni) "Mass flow rate of each connected unit at nominal conditions"; parameter Modelica.Fluid.Types.Dynamics energyDynamics=Modelica.Fluid.Types.Dynamics.FixedInitial "Type of energy balance (except for the pump always modeled in steady state)"; final parameter Modelica.Fluid.Types.Dynamics massDynamics=energyDynamics "Type of mass balance (except for the pump always modeled in steady state)"; parameter Modelica.SIunits.Time tau=120 "Time constant of fluid temperature variation at nominal flow rate"; // IO CONNECTORS Modelica.Fluid.Interfaces.FluidPorts_a ports_a1[nPorts_a1]( redeclare each final package Medium=Medium, each m_flow( min= if allowFlowReversal then -Modelica.Constants.inf else 0), each h_outflow( start=Medium.h_default, nominal=Medium.h_default)) "Terminal units return ports"; Modelica.Fluid.Interfaces.FluidPorts_b ports_b1[nPorts_b1]( redeclare each final package Medium=Medium, each m_flow( max= if allowFlowReversal then +Modelica.Constants.inf else 0), each h_outflow( start=Medium.h_default, nominal=Medium.h_default)) "Terminal units supply ports"; Modelica.Blocks.Interfaces.RealInput mReq_flow[nUni]( each final quantity="MassFlowRate") "Heating or chilled water flow rate required to meet the load"; Modelica.Blocks.Interfaces.IntegerInput modChaOve if have_val and typDis == Type_dis.ChangeOver "Operating mode in change-over (1 for heating, 2 for cooling)"; Modelica.Blocks.Interfaces.RealInput TSupSet( final quantity="ThermodynamicTemperature", final unit="K", displayUnit="degC") if have_val "Supply temperature set point"; Modelica.Blocks.Interfaces.RealOutput mReqTot_flow( final quantity="MassFlowRate", final unit="kg/s") "Total heating or chilled water flow rate required to meet the loads"; Modelica.Blocks.Interfaces.RealOutput QActTot_flow( final quantity="HeatFlowRate", final unit="W") "Total heat flow rate transferred to the loads (>=0 for heating)"; Modelica.Blocks.Interfaces.RealOutput PPum( final quantity="Power", final unit="W") if have_pum "Power drawn by pump motor"; // COMPONENTS Buildings.Controls.OBC.CDL.Continuous.MultiSum sumMasFloReq( final k=fill( 1, nUni), final nin=nUni) "Total required mass flow rate"; Buildings.Fluid.Sources.MassFlowSource_T sou_m_flow[nUni]( redeclare each final package Medium=Medium, each final use_m_flow_in=true, each final use_T_in=true, each final nPorts=1) "Source for terminal units supplied flow rate"; Buildings.Fluid.Sources.Boundary_pT sin( redeclare final package Medium=Medium, final nPorts=nUni) "Sink for terminal units return flow rate"; Buildings.Controls.OBC.CDL.Continuous.MultiSum Q_flowSum( final nin=nUni) "Total heat flow rate"; Modelica.Blocks.Sources.RealExpression mAct_flow[nUni]( final y( each final unit="kg/s")= if have_pum then mReq_flow else mReq_flow .* senMasFlo.m_flow/Buildings.Utilities.Math.Functions.smoothLimit( x=mReqTot_flow, l=m_flow_small, u=senMasFlo.m_flow, deltaX=m_flow_small)) "Actual supplied mass flow rate"; Modelica.Blocks.Sources.RealExpression QAct_flow[nUni]( final y( each final unit="W")=mAct_flow.y .*(ports_b1.h_outflow-inStream( ports_a1.h_outflow))) "Actual heat flow rate transferred to each load"; Buildings.Fluid.Actuators.Valves.ThreeWayEqualPercentageLinear val( redeclare final package Medium=Medium, final portFlowDirection_1= if allowFlowReversal then Modelica.Fluid.Types.PortFlowDirection.Bidirectional else Modelica.Fluid.Types.PortFlowDirection.Entering, final portFlowDirection_2= if allowFlowReversal then Modelica.Fluid.Types.PortFlowDirection.Bidirectional else Modelica.Fluid.Types.PortFlowDirection.Leaving, final portFlowDirection_3= if allowFlowReversal then Modelica.Fluid.Types.PortFlowDirection.Bidirectional else Modelica.Fluid.Types.PortFlowDirection.Entering, final dpValve_nominal=dpVal_nominal, final use_inputFilter=false, final m_flow_nominal=m_flow_nominal, final linearized={true,true}, energyDynamics=Modelica.Fluid.Types.Dynamics.FixedInitial) if have_val "Mixing valve"; Buildings.Fluid.Movers.BaseClasses.IdealSource pipPre( redeclare final package Medium=Medium, final dp_start=dp_nominal-dpVal_nominal, final m_flow_start=m_flow_nominal, final show_T=false, final show_V_flow=false, final control_m_flow=typCtr == Type_ctr.ConstantSpeed, final control_dp=typCtr <> Type_ctr.ConstantSpeed, final allowFlowReversal=allowFlowReversal, final m_flow_small=m_flow_small) "Fictitious pipe used to prescribe pump head or flow rate"; Buildings.Fluid.HeatExchangers.HeaterCooler_u heaCoo( redeclare final package Medium=Medium, final dp_nominal=0, final m_flow_nominal=m_flow_nominal, final Q_flow_nominal=-1, final allowFlowReversal=allowFlowReversal, final energyDynamics=energyDynamics, final massDynamics=massDynamics, final tau=tau) "Heat transfer from the terminal units to the distribution system"; Buildings.Fluid.FixedResistances.Junction spl( redeclare final package Medium=Medium, final portFlowDirection_1= if allowFlowReversal then Modelica.Fluid.Types.PortFlowDirection.Bidirectional else Modelica.Fluid.Types.PortFlowDirection.Entering, final portFlowDirection_2= if allowFlowReversal then Modelica.Fluid.Types.PortFlowDirection.Bidirectional else Modelica.Fluid.Types.PortFlowDirection.Leaving, final portFlowDirection_3= if allowFlowReversal then Modelica.Fluid.Types.PortFlowDirection.Bidirectional else Modelica.Fluid.Types.PortFlowDirection.Leaving, final m_flow_nominal=m_flow_nominal*{1,1,1}, final dp_nominal=0*{1,1,1}, energyDynamics=Modelica.Fluid.Types.Dynamics.FixedInitial) if have_val "Flow splitter"; Buildings.Fluid.Sensors.MassFlowRate senMasFlo( redeclare final package Medium=Medium, final allowFlowReversal=allowFlowReversal) "Supply mass flow rate sensor"; Buildings.Controls.OBC.CDL.Routing.RealReplicator reaRep( final nout=nUni) "Repeat input to output an array"; Controls.MixingValveControl conVal( final typDis=typDis) if have_val "Mixing valve controller"; Modelica.Blocks.Sources.RealExpression dpNetVal( final y( final unit="Pa")=dpPum-dpVal_nominal) "Pressure drop over the distribution network (excluding mixing valve)"; Modelica.Blocks.Sources.RealExpression masFloPum( final y( final unit="kg/s")=mPum_flow) "Pump mass flow rate value"; Modelica.Blocks.Sources.RealExpression spePum( final y( final unit="1")=spePum_nominal) "Pump speed (fractional)"; Buildings.Fluid.Movers.FlowControlled_m_flow pumFlo( redeclare final package Medium=Medium, per( final hydraulicEfficiency=per.hydraulicEfficiency, final motorEfficiency=per.motorEfficiency, final motorCooledByFluid=per.motorCooledByFluid, final speed_nominal=per.speed_nominal, final constantSpeed=per.constantSpeed, final speeds=per.speeds, final power=per.power), final allowFlowReversal=allowFlowReversal, final m_flow_nominal=m_flow_nominal, final dp_nominal=dp_nominal, addPowerToMedium=false, nominalValuesDefineDefaultPressureCurve=true, use_inputFilter=false, energyDynamics=Modelica.Fluid.Types.Dynamics.SteadyState) if have_pum and typCtr <> Type_ctr.ConstantSpeed "Distribution pump with prescribed mass flow rate"; Buildings.Fluid.Movers.SpeedControlled_y pumSpe( redeclare final package Medium=Medium, per( pressure( final V_flow=per.pressure.V_flow, final dp=per.pressure.dp), final hydraulicEfficiency=per.hydraulicEfficiency, final motorEfficiency=per.motorEfficiency, final motorCooledByFluid=per.motorCooledByFluid, final speed_nominal=per.speed_nominal, final constantSpeed=per.constantSpeed, final speeds=per.speeds, final power=per.power), final allowFlowReversal=allowFlowReversal, addPowerToMedium=false, use_inputFilter=false, energyDynamics=Modelica.Fluid.Types.Dynamics.SteadyState) if have_pum and typCtr == Type_ctr.ConstantSpeed "Distribution pump with prescribed speed (fractional)"; Fluid.Sensors.TemperatureTwoPort senTSup( redeclare final package Medium=Medium, final allowFlowReversal=allowFlowReversal, final m_flow_nominal=m_flow_nominal, initType=Modelica.Blocks.Types.Init.InitialState) "Supply temperature"; protected final parameter Modelica.SIunits.MassFlowRate mDis_flow_nominal[nUni]={sum(mUni_flow_nominal[i:nUni]) for i in 1:nUni} "Distribution flow rate between each connected unit at nominal conditions"; final parameter Real kDis[nUni]={ if dpDis_nominal[i] > Modelica.Constants.eps then mDis_flow_nominal[i]/sqrt(dpDis_nominal[i]) else Modelica.Constants.inf for i in 1:nUni} "Flow coefficient between each connected unit at nominal conditions"; Modelica.SIunits.MassFlowRate mDis_flow[nUni]={sum(mReq_flow[i:nUni]) for i in 1:nUni} "Distribution flow rate between each connected unit"; Modelica.SIunits.PressureDifference dpDis[nUni]=(mDis_flow ./ kDis) .^ 2 "Pressure drop between each connected unit (supply line)"; Modelica.SIunits.PressureDifference dpPum( displayUnit="Pa")= if typCtr == Type_ctr.LinearHead then dpMin+mPum_flow/m_flow_nominal*dp_nominal elseif typCtr == Type_ctr.ConstantDp then 2*sum( dpDis)+dpMin+dpVal_nominal else dp_nominal "Pump head"; Modelica.SIunits.MassFlowRate mPum_flow= if typCtr == Type_ctr.ConstantFlow then m_flow_nominal else sum( mReq_flow) "Pump mass flow rate"; parameter Medium.ThermodynamicState sta_default=Medium.setState_pTX( T=Medium.T_default, p=Medium.p_default, X=Medium.X_default); parameter Modelica.SIunits.Density rho_default=Medium.density( sta_default) "Density, used to compute fluid volume"; initial equation assert( nPorts_a1 == nPorts_b1, "In "+getInstanceName()+": The numbers of terminal units return ports ("+String( nPorts_a1)+") and supply ports ("+String( nPorts_b1)+") must be equal."); assert( if have_val then have_pum else true, "In "+getInstanceName()+": The configuration where have_val is true and have_pum is false is not allowed."); equation // Connect statements involving conditionally removed components are // removed at translation time by Modelica specification. // Only obsolete statements corresponding to the default model structure need // to be programmatically removed. if not have_val then connect(heaCoo.port_b,port_b); connect(port_a,pumFlo.port_a); connect(port_a,pumSpe.port_a); end if; if not have_pum then connect(port_a,senTSup.port_a); end if; connect(sumMasFloReq.y,mReqTot_flow); connect(mReq_flow,sumMasFloReq.u); connect(mAct_flow.y,sou_m_flow.m_flow_in); connect(ports_a1,sin.ports); connect(sou_m_flow.ports[1],ports_b1); connect(senMasFlo.port_b,heaCoo.port_a); connect(Q_flowSum.y,QActTot_flow); connect(QAct_flow.y,Q_flowSum.u); connect(Q_flowSum.y,heaCoo.u); connect(reaRep.y,sou_m_flow.T_in); connect(port_a,val.port_1); connect(heaCoo.port_b,spl.port_1); connect(spl.port_2,port_b); connect(spl.port_3,val.port_3); connect(TSupSet,conVal.TSupSet); connect(conVal.yVal,val.y); connect(modChaOve,conVal.modChaOve); connect(val.port_2,pumFlo.port_a); connect(val.port_2,pumSpe.port_a); connect(pumFlo.P,PPum); connect(pumSpe.P,PPum); connect(dpNetVal.y,pipPre.dp_in); connect(masFloPum.y,pipPre.m_flow_in); connect(masFloPum.y,pumFlo.m_flow_in); connect(spePum.y,pumSpe.y); connect(pipPre.port_a,senTSup.port_b); connect(pumSpe.port_b,senTSup.port_a); connect(pumFlo.port_b,senTSup.port_a); connect(senTSup.T,reaRep.u); connect(senTSup.T,conVal.TSupMes); connect(pipPre.port_b,senMasFlo.port_a); end FlowDistribution;

Buildings.Experimental.DHC.Loads.SimpleRoomODE

Simplified model for assessing room air temperature variations around a set point

Buildings.Experimental.DHC.Loads.SimpleRoomODE

Information

This is a first order ODE model assessing the indoor air temperature variations around a set point, based on the difference between the required and actual heating or cooling heat flow rate and a minimum set of parameters at nominal conditions.

The lumped thermal conductance G representing all heat transfer mechanisms that depend on the temperature difference with the outside (transmission, infiltration and ventilation) is assessed from the steady-state energy balance at heating nominal conditions as

0 = Q̇_{heating, nom} + G (T_{out, heating, nom} - T_{ind, heating, nom}).

Note that it is important for the model representativeness that Q̇_{heating, nom} be evaluated in close to steady-state conditions with no internal heat gains and no solar heat gains.

The lumped thermal conductance G is then considered constant for all operating conditions.

The required heating or cooling heat flow rate (i.e. the space load) Q̇_{heat_cool, req} corresponds to a steady-state control error equal to zero,

0 = Q̇_{heat_cool, req} + G (T_out - T_{ind, set}) + Q̇_various,

where Q̇_various represent the miscellaneous heat gains. The indoor temperature variation rate due to an unmet load is given by

C ∂T_ind / ∂t = Q̇_{heat_cool, act} + G (T_out - T_ind) + Q̇_various,

where Q̇_{heat_cool, act} is the actual heating or cooling heat flow rate and C is the thermal capacitance of the indoor volume. The two previous equations yield

τ ∂T_ind / ∂t = (Q̇_{heat_cool, act} - Q̇_{heat_cool, req}) / G - T_ind + T_{ind, set},

where τ = C / G is the time constant of the indoor temperature.

Extends from Modelica.Blocks.Icons.Block (Basic graphical layout of input/output block).

Parameters

Type	Name	Default	Description
Time	tau	1800	Time constant of the indoor temperature [s]
Nominal condition
Temperature	TOutHea_nominal		Outdoor air temperature at heating nominal conditions [K]
Temperature	TIndHea_nominal		Indoor air temperature at heating nominal conditions [K]
HeatFlowRate	QHea_flow_nominal		Heating heat flow rate (for TInd=TIndHea_nominal, TOut=TOutHea_nominal, with no internal gains, no solar radiation) [W]
Initialization
Boolean	steadyStateInitial	false	true initializes T with dT(0)/dt=0, false initializes T with T(0)=TIndHea_nominal

Connectors

Type	Name	Description
input RealInput	TSet	Temperature set point for heating or cooling [K]
input RealInput	QReq_flow	Required heat flow rate to meet temperature set point (>=0 for heating) [W]
input RealInput	QAct_flow	Actual heating or cooling heat flow rate (>=0 for heating) [W]
output RealOutput	TAir	Room air temperature [K]

Modelica definition

model SimpleRoomODE "Simplified model for assessing room air temperature variations around a set point" extends Modelica.Blocks.Icons.Block; parameter Modelica.SIunits.Temperature TOutHea_nominal( displayUnit="degC") "Outdoor air temperature at heating nominal conditions"; parameter Modelica.SIunits.Temperature TIndHea_nominal( displayUnit="degC") "Indoor air temperature at heating nominal conditions"; parameter Modelica.SIunits.HeatFlowRate QHea_flow_nominal( min=0) "Heating heat flow rate (for TInd=TIndHea_nominal, TOut=TOutHea_nominal, with no internal gains, no solar radiation)"; parameter Boolean steadyStateInitial=false "true initializes T with dT(0)/dt=0, false initializes T with T(0)=TIndHea_nominal"; parameter Modelica.SIunits.Time tau=1800 "Time constant of the indoor temperature"; Modelica.Blocks.Interfaces.RealInput TSet( final quantity="ThermodynamicTemperature", final unit="K", displayUnit="degC") "Temperature set point for heating or cooling"; Modelica.Blocks.Interfaces.RealInput QReq_flow( final quantity="HeatFlowRate", final unit="W") "Required heat flow rate to meet temperature set point (>=0 for heating)"; Modelica.Blocks.Interfaces.RealInput QAct_flow( final quantity="HeatFlowRate", final unit="W") "Actual heating or cooling heat flow rate (>=0 for heating)"; Modelica.Blocks.Interfaces.RealOutput TAir( final quantity="ThermodynamicTemperature", final unit="K", displayUnit="degC") "Room air temperature"; protected parameter Modelica.SIunits.ThermalConductance G=-QHea_flow_nominal/(TOutHea_nominal-TIndHea_nominal) "Lumped thermal conductance representing all temperature dependent heat transfer mechanisms"; initial equation if steadyStateInitial then der( TAir)=0; else TAir=TIndHea_nominal; end if; equation der( TAir)*tau=(QAct_flow-QReq_flow)/G+TSet-TAir; assert( TAir >= 273.15, "In "+getInstanceName()+": The computed indoor temperature is below 0°C."); end SimpleRoomODE;