Buildings.Controls.OBC.CDL.Continuous
Package with blocks for continuous variables
Information
Package with blocks for elementary mathematical functions for continuous variables.
Package Content
| Name | Description |
|---|---|
| Output the absolute value of the input | |
| Output the sum of the two inputs | |
| Output the sum of an input plus a parameter | |
| Output the arc tangent of the input | |
| Output atan(u1/u2) of the inputs u1 and u2 | |
| Output the average of its two inputs | |
| Output the cosine of the input | |
| Output first input divided by second input | |
| Output the exponential (base e) of the input | |
| Output difference between commanded and feedback input | |
| Output the product of a gain value with the input signal | |
| Output y is true, if input u1 is greater than input u2 | |
| Output y is true, if input u is greater than threshold | |
| Transform Real to Boolean signal with Hysteresis | |
| Output the integral of the input signal | |
| Output y is true, if input u1 is less than input u2 | |
| Output y is true, if input u is less than threshold | |
| Limit the range of a signal | |
| Output the value of the input x along a line specified by two points | |
| Output the natural (base e) logarithm of the input (input > 0 required) | |
| Output the base 10 logarithm of the input (input > 0 required) | |
| Output the product of a gain matrix with the input signal vector | |
| Output vector of row- or column-wise maximum of the input matrix | |
| Output vector of row- or column-wise minimum values | |
| Pass through the largest signal | |
| Pass through the smallest signal | |
| Output the remainder of first input divided by second input (~=0) | |
| Block to output moving average | |
| Output the maximum element of the input vector | |
| Output the minimum element of the input vector | |
| Sum of Reals, y = k[1]*u[1] + k[2]*u[2] + ... + k[n]*u[n] | |
| P, PI, PD, and PID controller | |
| P, PI, PD, and PID controller with output reset | |
| Output product of the two inputs | |
| Round real number to given digits | |
| Output the sine of the input | |
| Limit the increase or decrease rate of input | |
| Sort elements of input vector in ascending or descending order | |
| Output the square root of the input (input >= 0 required) | |
| Output the tangent of the input | |
| Package with blocks that generate source signals | |
| Collection of models that validate the continuous blocks of the CDL |
 Buildings.Controls.OBC.CDL.Continuous.Abs
Buildings.Controls.OBC.CDL.Continuous.Abs
Output the absolute value of the input

Information
Block that outputs y = abs(u),
where
u is an input.
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Connector of Real input signal |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Add
Buildings.Controls.OBC.CDL.Continuous.Add
Output the sum of the two inputs

Information
Block that outputs y as the weighted sum of the
two input signals u1 and u2,
y = k1*u1 + k2*u2;
where k1 and k2 are parameters.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | k1 | +1 | Gain for input u1 |
| Real | k2 | +1 | Gain for input u2 |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u1 | Connector of Real input signal 1 |
| input RealInput | u2 | Connector of Real input signal 2 |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.AddParameter
Buildings.Controls.OBC.CDL.Continuous.AddParameter
Output the sum of an input plus a parameter

Information
Block that outputs y = k u + p,
where k and p are
parameters and u is an input.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | p | Value to be added | |
| Real | k | Gain of input |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Connector of Real input signal |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Atan
Buildings.Controls.OBC.CDL.Continuous.Atan
Output the arc tangent of the input

Information
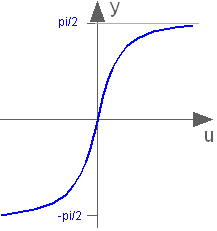
Block that outputs y = atan(u),
where
u is an input.
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Connector of Real input signal |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Atan2
Buildings.Controls.OBC.CDL.Continuous.Atan2
Output atan(u1/u2) of the inputs u1 and u2

Information
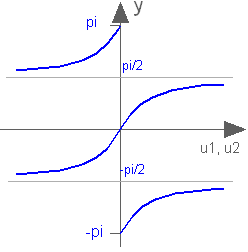
Block that outputs the tangent-inverse y = atan2(u1, u2)
of the input u1 divided by the input u2.
u1 and u2 shall not be zero at the same time instant.
Atan2 uses the sign of u1 and u2
in order to construct the solution in the range
-π ≤ y ≤ π, whereas
Buildings.Controls.OBC.CDL.Continuous.Atan
gives a solution in the range
-π/2 ≤ y ≤ π/2.
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u1 | Connector of Real input signal 1 |
| input RealInput | u2 | Connector of Real input signal 2 |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Average
Buildings.Controls.OBC.CDL.Continuous.Average
Output the average of its two inputs

Information
Block that outputs y = avg(u1,u2),
where
u1 and u2 are inputs.
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u1 | Connector of Real input signal 1 |
| input RealInput | u2 | Connector of Real input signal 2 |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Cos
Buildings.Controls.OBC.CDL.Continuous.Cos
Output the cosine of the input

Information
Block that outputs y = cos(u),
where
u is an input.
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Connector of Real input signal |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Division
Buildings.Controls.OBC.CDL.Continuous.Division
Output first input divided by second input

Information
Block that outputs y = u1 / u2,
where
u1 and u2 are inputs.
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u1 | Connector of Real input signal 1 |
| input RealInput | u2 | Connector of Real input signal 2 |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Exp
Buildings.Controls.OBC.CDL.Continuous.Exp
Output the exponential (base e) of the input

Information
Block that outputs y = exp(u),
where
u is an input and exp() is the
base-e exponential function.
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Connector of Real input signal |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Feedback
Buildings.Controls.OBC.CDL.Continuous.Feedback
Output difference between commanded and feedback input
Information
Block that outputs y = u1 - u2,
where
u1 and u2 are inputs.
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u1 | Connector of Real input signal 1 |
| input RealInput | u2 | Connector of Real input signal 2 |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Gain
Buildings.Controls.OBC.CDL.Continuous.Gain
Output the product of a gain value with the input signal

Information
Block that outputs y = k * u,
where
k is a parameter and
u is an input.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | k | Gain value multiplied with input signal |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Input signal connector |
| output RealOutput | y | Output signal connector |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Greater
Buildings.Controls.OBC.CDL.Continuous.Greater
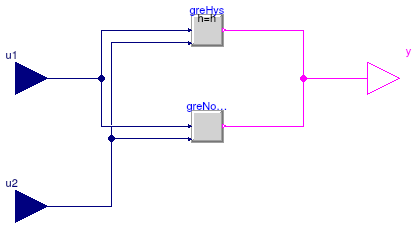
Output y is true, if input u1 is greater than input u2
Information
Block that outputs true if the Real input u1
is greater than the Real input u2, optionally within a hysteresis h.
The parameter h ≥ 0 is used to specify a hysteresis.
If h ≠ 0, then the output switches to true if u1 > u2,
and it switches to false if u1 < u2 - h.
If h = 0, the output is y=u1 > u2.
Enabling hysteresis can avoid frequent switching.
Adding hysteresis is recommended in real controllers to guard against sensor noise, and
in simulation to guard against numerical noise. Numerical noise can be present if
an input depends on a state variable or a quantity that requires an iterative solution, such as
a temperature or a mass flow rate of an HVAC system.
To disable hysteresis, set h=0.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | h | 0 | Hysteresis |
| Advanced | |||
| Boolean | pre_y_start | false | Value of pre(y) at initial time |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u1 | Input u1 |
| input RealInput | u2 | Input u2 |
| output BooleanOutput | y | Output y |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.GreaterThreshold
Buildings.Controls.OBC.CDL.Continuous.GreaterThreshold
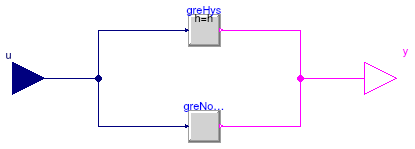
Output y is true, if input u is greater than threshold
Information
Block that outputs true if the Real input u
is greater than a threshold t, optionally within a hysteresis h.
The parameter h ≥ 0 is used to specify a hysteresis.
If h ≠ 0, then the output switches to true if u > t,
where t is the threshold,
and it switches to false if u < t - h.
If h = 0, the output is y = u > t.
Enabling hysteresis can avoid frequent switching.
Adding hysteresis is recommended in real controllers to guard against sensor noise, and
in simulation to guard against numerical noise. Numerical noise can be present if
an input depends on a state variable or a quantity that requires an iterative solution, such as
a temperature or a mass flow rate of an HVAC system.
To disable hysteresis, set h=0.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | t | 0 | Threshold for comparison |
| Real | h | 0 | Hysteresis |
| Advanced | |||
| Boolean | pre_y_start | false | Value of pre(y) at initial time |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Input |
| output BooleanOutput | y | Output |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Hysteresis
Buildings.Controls.OBC.CDL.Continuous.Hysteresis
Transform Real to Boolean signal with Hysteresis

Information
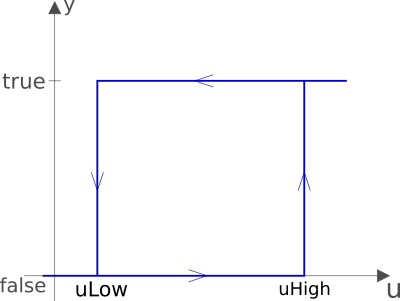
Block that transforms a Real input signal into a Boolean
output signal:
- When the output was
falseand the input becomes greater than the parameteruHigh, the output switches totrue. - When the output was
trueand the input becomes less than the parameteruLow, the output switches tofalse.
The start value of the output is defined via parameter
pre_y_start (= value of pre(y) at initial time).
The default value of this parameter is false.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | uLow | if y=true and u<uLow, switch to y=false | |
| Real | uHigh | if y=false and u>uHigh, switch to y=true | |
| Boolean | pre_y_start | false | Value of pre(y) at initial time |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Real input signal |
| output BooleanOutput | y | Boolean output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.IntegratorWithReset
Buildings.Controls.OBC.CDL.Continuous.IntegratorWithReset
Output the integral of the input signal

Information
This model is similar to
Modelica.Blocks.Continuous.Integrator
except that it allows to reset the output y
of the integrator.
The output of the integrator can be reset as follows:
-
Whenever the input signal
triggerchanges fromfalsetotrue, the integrator is reset by settingyto the value of the input signaly_reset_in.
Implementation
To adjust the icon layer, the code of Modelica.Blocks.Continuous.Integrator has been copied into this model rather than extended.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | k | 1 | Integrator gain [1] |
| Initialization | |||
| Real | y_start | 0 | Initial or guess value of output (= state) |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Connector of Real input signal |
| input RealInput | y_reset_in | Input signal for state to which integrator is reset |
| input BooleanInput | trigger | Resets the integrator output when trigger becomes true |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Less
Buildings.Controls.OBC.CDL.Continuous.Less
Output y is true, if input u1 is less than input u2
Information
Block that outputs true if the Real input u1
is less than the Real input u2, optionally within a hysteresis h.
The parameter h ≥ 0 is used to specify a hysteresis.
If h ≠ 0, then the output switches to true if u1 < u2,
and it switches to false if u1 > u2 + h.
If h = 0, the output is y = u1 < u2.
Enabling hysteresis can avoid frequent switching. Adding hysteresis is recommended in real controllers to guard against sensor noise, and in simulation to guard against numerical noise. Numerical noise can be present if an input depends on a state variable or a quantity that requires an iterative solution, such as a temperature or a mass flow rate of an HVAC system. To disable hysteresis, set h=0.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | h | 0 | Hysteresis |
| Advanced | |||
| Boolean | pre_y_start | false | Value of pre(y) at initial time |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u1 | Input u1 |
| input RealInput | u2 | Input u2 |
| output BooleanOutput | y | Output y |
Modelica definition
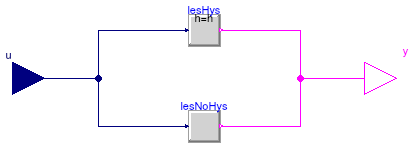
 Buildings.Controls.OBC.CDL.Continuous.LessThreshold
Buildings.Controls.OBC.CDL.Continuous.LessThreshold
Output y is true, if input u is less than threshold
Information
Block that outputs true if the Real input u
is less than a threshold t, optionally within a hysteresis h.
The parameter h ≥ 0 is used to specify a hysteresis.
If h ≠ 0, then the output switches to true if u < t,
where t is the threshold,
and it switches to false if u > t + h.
If h = 0, the output is y = u < t.
Enabling hysteresis can avoid frequent switching. Adding hysteresis is recommended in real controllers to guard against sensor noise, and in simulation to guard against numerical noise. Numerical noise can be present if an input depends on a state variable or a quantity that requires an iterative solution, such as a temperature or a mass flow rate of an HVAC system. To disable hysteresis, set h=0.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | t | 0 | Threshold for comparison |
| Real | h | 0 | Hysteresis |
| Advanced | |||
| Boolean | pre_y_start | false | Value of pre(y) at initial time |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Input |
| output BooleanOutput | y | Output |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Limiter
Buildings.Controls.OBC.CDL.Continuous.Limiter
Limit the range of a signal

Information
Block that outputs y = min(uMax, max(uMin, u)),
where
u is an input
and
uMax and uMin are parameters.
If uMax < uMin, an error occurs and no output is produced.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | uMax | Upper limit of input signal | |
| Real | uMin | Lower limit of input signal |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Connector of Real input signal |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Line
Buildings.Controls.OBC.CDL.Continuous.Line
Output the value of the input x along a line specified by two points

Information
Block that outputs y = a + b u,
where
u is an input
and the coefficients a and b
are determined so that the line intercepts the two input points
specified by the two points x1 and f1,
and x2 and f2.
The parameters limitBelow and limitAbove
determine whether x1 and x2 are also used
to limit the input u.
If the limits are used, then this block requires x1 < x2.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Boolean | limitBelow | true | If true, limit input u to be no smaller than x1 |
| Boolean | limitAbove | true | If true, limit input u to be no larger than x2 |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | x1 | Support point x1, with x1 < x2 |
| input RealInput | f1 | Support point f(x1) |
| input RealInput | x2 | Support point x2, with x2 > x1 |
| input RealInput | f2 | Support point f(x2) |
| input RealInput | u | Independent variable |
| output RealOutput | y | f(x) along the line specified by (x1, f1) and (x2, f2) |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Log
Buildings.Controls.OBC.CDL.Continuous.Log
Output the natural (base e) logarithm of the input (input > 0 required)

Information
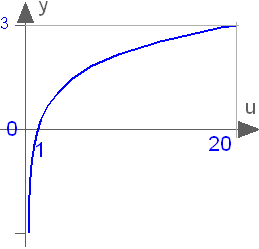
Block that outputs y = log(u),
where
u is an input and log() is the
natural logarithm (base-e) function.
An error occurs if the input u is
zero or negative.
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Connector of Real input signal |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Log10
Buildings.Controls.OBC.CDL.Continuous.Log10
Output the base 10 logarithm of the input (input > 0 required)

Information
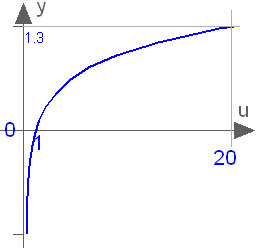
Block that outputs y = log10(u),
where
u is an input and log10() is the
logarithm (base-10) function.
An error occurs if the input u is
zero or negative.
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Connector of Real input signal |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.MatrixGain
Buildings.Controls.OBC.CDL.Continuous.MatrixGain
Output the product of a gain matrix with the input signal vector
Information
This blocks computes output vector y as the product of the gain matrix K with the input signal vector u as y = K u. For example,
parameter Real K[:,:] = [0.12 2; 3 1.5];
results in
| y[1] | | 0.12 2.00 | | u[1] |
| | = | | * | |
| y[2] | | 3.00 1.50 | | u[2] |
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | K[:, :] | [1, 0; 0, 1] | Gain matrix which is multiplied with the input |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u[nin] | Connector of Real input signals |
| output RealOutput | y[nout] | Connector of Real output signals |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.MatrixMax
Buildings.Controls.OBC.CDL.Continuous.MatrixMax
Output vector of row- or column-wise maximum of the input matrix

Information
If rowMax = true, this block outputs the row-wise maximum
of the input matrix u,
otherwise it outputs the column-wise maximum of the input matrix u.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Boolean | rowMax | true | If true, outputs row-wise maximum, otherwise column-wise |
| Integer | nRow | Number of rows in input matrix | |
| Integer | nCol | Number of columns in input matrix |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u[nRow, nCol] | Connector of Real input signals |
| output RealOutput | y[if rowMax then size(u, 1) else size(u, 2)] | Connector of Real output signals |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.MatrixMin
Buildings.Controls.OBC.CDL.Continuous.MatrixMin
Output vector of row- or column-wise minimum values

Information
If rowMin = true, this block outputs the row-wise minimum
of the input matrix u,
otherwise it outputs the column-wise minimum of the input matrix u.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Boolean | rowMin | true | If true, outputs row-wise minimum, otherwise column-wise |
| Integer | nRow | Number of rows in input matrix | |
| Integer | nCol | Number of columns in input matrix |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u[nRow, nCol] | Connector of Real input signals |
| output RealOutput | y[if rowMin then size(u, 1) else size(u, 2)] | Connector of Real output signals |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Max
Buildings.Controls.OBC.CDL.Continuous.Max
Pass through the largest signal

Information
Block that outputs y = max(u1, u2),
where
u1 and u2 are inputs.
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u1 | Connector of Real input signal 1 |
| input RealInput | u2 | Connector of Real input signal 2 |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Min
Buildings.Controls.OBC.CDL.Continuous.Min
Pass through the smallest signal

Information
Block that outputs y = min(u1, u2),
where
u1 and u2 are inputs.
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u1 | Connector of Real input signal 1 |
| input RealInput | u2 | Connector of Real input signal 2 |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Modulo
Buildings.Controls.OBC.CDL.Continuous.Modulo
Output the remainder of first input divided by second input (~=0)

Information
Block that outputs y = mod(u1/u2),
where
u1 and u2 are inputs.
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u1 | Connector of Real input signal 1 |
| input RealInput | u2 | Connector of Real input signal 2 |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.MovingMean
Buildings.Controls.OBC.CDL.Continuous.MovingMean
Block to output moving average

Information
This block outputs the mean value of its input signal as
1 t
y = - ∫ u(s) ds
δ t-δ
where δ is a parameter that determines the time window over which the input is averaged. For t < δ seconds, it outputs
1 t
y = -------- ∫ u(s) ds
t-t0+10-10 t0
where t0 is the initial time.
This block can for example be used to output the moving average of a noisy measurement signal.
See Buildings.Controls.OBC.CDL.Continuous.Validation.MovingMean and Buildings.Controls.OBC.CDL.Continuous.Validation.MovingMean_nonZeroStart for example.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | delta | Time horizon over which the input is averaged [s] |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Connector of Real input signal |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.MultiMax
Buildings.Controls.OBC.CDL.Continuous.MultiMax
Output the maximum element of the input vector

Information
Outputs the maximum element of the input vector.
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u[nin] | Connector of Real input signals |
| output RealOutput | y | Connector of Real output signals |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.MultiMin
Buildings.Controls.OBC.CDL.Continuous.MultiMin
Output the minimum element of the input vector

Information
Outputs the minimum element of the input vector.
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u[nin] | Connector of Real input signals |
| output RealOutput | y | Connector of Real output signals |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.MultiSum
Buildings.Controls.OBC.CDL.Continuous.MultiSum
Sum of Reals, y = k[1]*u[1] + k[2]*u[2] + ... + k[n]*u[n]

Information
Block that outputs
y = ∑i=1n ki ui,
where k is a parameter with n elements and u is an input of the same length. The dimension of u can be enlarged by drawing an additional connection line. The connection is automatically connected to this new free index.
If no connection to the input connector u is present, the output is y=0.
See Buildings.Controls.OBC.CDL.Continuous.Validation.MultiSum for an example.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | k[nin] | fill(1, nin) | Input gains |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u[nin] | Connector of Real input signals |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.PID
Buildings.Controls.OBC.CDL.Continuous.PID
P, PI, PD, and PID controller
Information
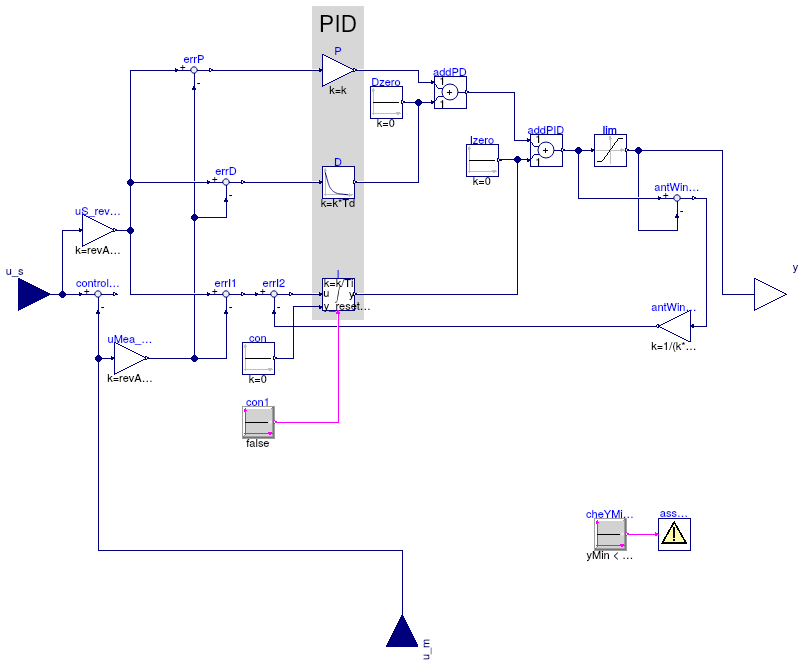
PID controller in the standard form
yu = k/r (e(t) + 1 ⁄ Ti ∫ e(τ) dτ + Td d⁄dt e(t)),
where yu is the control signal before output limitation, e(t) = us(t) - um(t) is the control error, with us being the set point and um being the measured quantity, k is the gain, Ti is the time constant of the integral term, Td is the time constant of the derivative term, and r is a scaling factor, with default r=1. The scaling factor should be set to the typical order of magnitude of the range of the error e. For example, you may set r=100 to r=1000 if the control input is a pressure of a heating water circulation pump in units of Pascal, or leave r=1 if the control input is a room temperature.
Note that the units of k are the inverse of the units of the control error, while the units of Ti and Td are seconds.
The actual control output is
y = min( ymax, max( ymin, y)),
where ymin and ymax are limits for the control signal.
P, PI, PD, or PID action
Through the parameter controllerType, the controller can be configured
as P, PI, PD or PID controller. The default configuration is PI.
Reverse or direct action
Through the parameter reverseActing, the controller can be configured to
be reverse or direct acting.
The above standard form is reverse acting, which is the default configuration.
For a reverse acting controller, for a constant set point,
an increase in measurement signal u_m decreases the control output signal y
(Montgomery and McDowall, 2008).
Thus,
-
for a heating coil with a two-way valve, leave
reverseActing = true, but -
for a cooling coil with a two-way valve, set
reverseActing = false.
If reverseAction=false, then the error e above is multiplied by -1.
Anti-windup compensation
The controller anti-windup compensation is as follows: Instead of the above basic control law, the implementation is
yu = k (e(t) ⁄ r + 1 ⁄ Ti ∫ (-Δy + e(τ) ⁄ r) dτ + Td ⁄ r d⁄dt e(t)),
where the anti-windup compensation Δy is
Δy = (yu - y) ⁄ (k Ni),
where Ni > 0 is the time constant for the anti-windup compensation. To accelerate the anti-windup, decrease Ni.
Note that the anti-windup term (-Δy + e(τ) ⁄ r) shows that the range of the typical control error r should be set to a reasonable value so that
e(τ) ⁄ r = (us(τ) - um(τ)) ⁄ r
has order of magnitude one, and hence the anti-windup compensation should work well.
Reset of the controller output
Note that this controller implements an integrator anti-windup. Therefore, for most applications, the controller output does not need to be reset. However, if the controller is used in conjuction with equipment that is being switched on, better control performance may be achieved by resetting the controller output when the equipment is switched on. This is in particular the case in situations where the equipment control input should continuously increase as the equipment is switched on, such as a light dimmer that may slowly increase the luminance, or a variable speed drive of a motor that should continuously increase the speed. In this case, the controller Buildings.Controls.OBC.CDL.Continuous.PIDWithReset that can reset the output should be used.
Approximation of the derivative term
The derivative of the control error d ⁄ dt e(t) is approximated using
d⁄dt x(t) = (e(t)-x(t)) Td ⁄ Nd,
and
d⁄dt e(t) ≈ Nd (e(t)-x(t)),
where x(t) is an internal state.
Guidance for tuning the control gains
The parameters of the controller can be manually adjusted by performing closed loop tests (= controller + plant connected together) and using the following strategy:
- Set very large limits, e.g., set ymax = 1000.
-
Select a P-controller and manually enlarge the parameter
k(the total gain of the controller) until the closed-loop response cannot be improved any more. -
Select a PI-controller and manually adjust the parameters
kandTi(the time constant of the integrator). The first value ofTican be selected such that it is in the order of the time constant of the oscillations occurring with the P-controller. If, e.g., oscillations in the order of 100 seconds occur in the previous step, start withTi=1/100seconds. -
If you want to make the reaction of the control loop faster
(but probably less robust against disturbances and measurement noise)
select a PID-controller and manually adjust parameters
k,Ti,Td(time constant of derivative block). -
Set the limits
yMaxandyMinaccording to your specification. -
Perform simulations such that the output of the PID controller
goes in its limits. Tune
Ni(Ni Ti is the time constant of the anti-windup compensation) such that the input to the limiter block (=lim.u) goes quickly enough back to its limits. IfNiis decreased, this happens faster. IfNiis very large, the anti-windup compensation is not effective and the controller works bad.
References
R. Montgomery and R. McDowall (2008). "Fundamentals of HVAC Control Systems." American Society of Heating Refrigerating and Air-Conditioning Engineers Inc. Atlanta, GA.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| SimpleController | controllerType | Buildings.Controls.OBC.CDL.T... | Type of controller |
| Real | r | 1 | Typical range of control error, used for scaling the control error |
| Boolean | reverseActing | true | Set to true for reverse acting, or false for direct acting control action |
| Control gains | |||
| Real | k | 1 | Gain of controller |
| Real | Ti | 0.5 | Time constant of integrator block [s] |
| Real | Td | 0.1 | Time constant of derivative block [s] |
| Limits | |||
| Real | yMax | 1 | Upper limit of output |
| Real | yMin | 0 | Lower limit of output |
| Advanced | |||
| Integrator anti-windup | |||
| Real | Ni | 0.9 | Ni*Ti is time constant of anti-windup compensation |
| Derivative block | |||
| Real | Nd | 10 | The higher Nd, the more ideal the derivative block |
| Initialization | |||
| Real | xi_start | 0 | Initial value of integrator state |
| Real | yd_start | 0 | Initial value of derivative output |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u_s | Connector of setpoint input signal |
| input RealInput | u_m | Connector of measurement input signal |
| output RealOutput | y | Connector of actuator output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.PIDWithReset
Buildings.Controls.OBC.CDL.Continuous.PIDWithReset
P, PI, PD, and PID controller with output reset
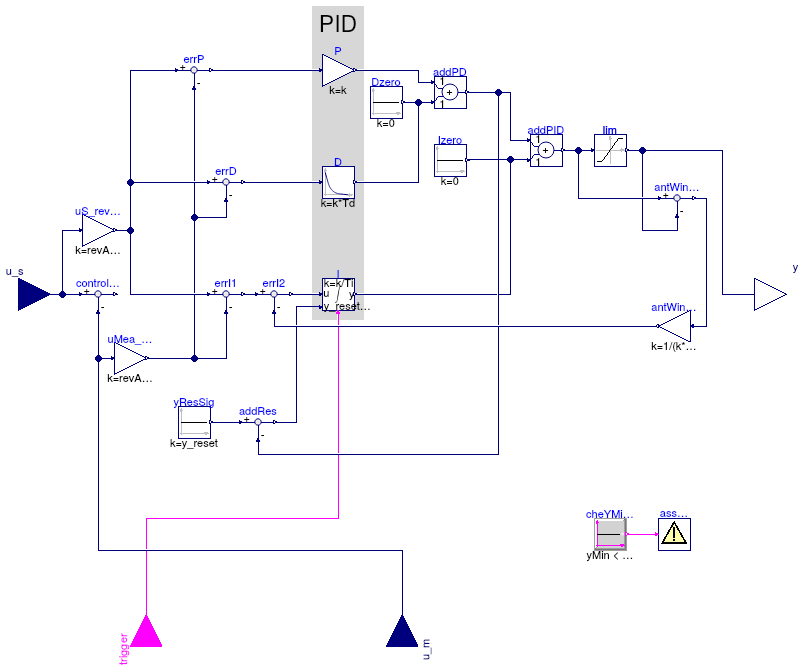
Information
PID controller in the standard form
yu = k/r (e(t) + 1 ⁄ Ti ∫ e(τ) dτ + Td d⁄dt e(t)),
with output reset, where yu is the control signal before output limitation, e(t) = us(t) - um(t) is the control error, with us being the set point and um being the measured quantity, k is the gain, Ti is the time constant of the integral term, Td is the time constant of the derivative term, and r is a scaling factor, with default r=1. The scaling factor should be set to the typical order of magnitude of the range of the error e. For example, you may set r=100 to r=1000 if the control input is a pressure of a heating water circulation pump in units of Pascal, or leave r=1 if the control input is a room temperature.
Note that the units of k are the inverse of the units of the control error, while the units of Ti and Td are seconds.
The actual control output is
y = min( ymax, max( ymin, y)),
where ymin and ymax are limits for the control signal.
P, PI, PD, or PID action
Through the parameter controllerType, the controller can be configured
as P, PI, PD or PID controller. The default configuration is PI.
Reverse or direct action
Through the parameter reverseActing, the controller can be configured to
be reverse or direct acting.
The above standard form is reverse acting, which is the default configuration.
For a reverse acting controller, for a constant set point,
an increase in measurement signal u_m decreases the control output signal y
(Montgomery and McDowall, 2008).
Thus,
-
for a heating coil with a two-way valve, leave
reverseActing = true, but -
for a cooling coil with a two-way valve, set
reverseActing = false.
If reverseAction=false, then the error e above is multiplied by -1.
Anti-windup compensation
The controller anti-windup compensation is as follows: Instead of the above basic control law, the implementation is
yu = k (e(t) ⁄ r + 1 ⁄ Ti ∫ (-Δy + e(τ) ⁄ r) dτ + Td ⁄ r d⁄dt e(t)),
where the anti-windup compensation Δy is
Δy = (yu - y) ⁄ (k Ni),
where Ni > 0 is the time constant for the anti-windup compensation. To accelerate the anti-windup, decrease Ni.
Note that the anti-windup term (-Δy + e(τ) ⁄ r) shows that the range of the typical control error r should be set to a reasonable value so that
e(τ) ⁄ r = (us(τ) - um(τ)) ⁄ r
has order of magnitude one, and hence the anti-windup compensation should work well.
Reset of the controller output
Whenever the value of boolean input signal trigger changes from
false to true, the controller output is reset by setting
y to the value of the parameter y_reset.
Approximation of the derivative term
The derivative of the control error d ⁄ dt e(t) is approximated using
d⁄dt x(t) = (e(t)-x(t)) Td ⁄ Nd,
and
d⁄dt e(t) ≈ Nd (e(t)-x(t)),
where x(t) is an internal state.
Guidance for tuning the control gains
The parameters of the controller can be manually adjusted by performing closed loop tests (= controller + plant connected together) and using the following strategy:
- Set very large limits, e.g., set ymax = 1000.
-
Select a P-controller and manually enlarge the parameter
k(the total gain of the controller) until the closed-loop response cannot be improved any more. -
Select a PI-controller and manually adjust the parameters
kandTi(the time constant of the integrator). The first value ofTican be selected such that it is in the order of the time constant of the oscillations occurring with the P-controller. If, e.g., oscillations in the order of 100 seconds occur in the previous step, start withTi=1/100seconds. -
If you want to make the reaction of the control loop faster
(but probably less robust against disturbances and measurement noise)
select a PID-controller and manually adjust parameters
k,Ti,Td(time constant of derivative block). -
Set the limits
yMaxandyMinaccording to your specification. -
Perform simulations such that the output of the PID controller
goes in its limits. Tune
Ni(Ni Ti is the time constant of the anti-windup compensation) such that the input to the limiter block (=lim.u) goes quickly enough back to its limits. IfNiis decreased, this happens faster. IfNiis very large, the anti-windup compensation is not effective and the controller works bad.
References
R. Montgomery and R. McDowall (2008). "Fundamentals of HVAC Control Systems." American Society of Heating Refrigerating and Air-Conditioning Engineers Inc. Atlanta, GA.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| SimpleController | controllerType | Buildings.Controls.OBC.CDL.T... | Type of controller |
| Real | r | 1 | Typical range of control error, used for scaling the control error |
| Boolean | reverseActing | true | Set to true for reverse acting, or false for direct acting control action |
| Control gains | |||
| Real | k | 1 | Gain of controller |
| Real | Ti | 0.5 | Time constant of integrator block [s] |
| Real | Td | 0.1 | Time constant of derivative block [s] |
| Limits | |||
| Real | yMax | 1 | Upper limit of output |
| Real | yMin | 0 | Lower limit of output |
| Integrator reset | |||
| Real | y_reset | xi_start | Value to which the controller output is reset if the boolean trigger has a rising edge |
| Advanced | |||
| Integrator anti-windup | |||
| Real | Ni | 0.9 | Ni*Ti is time constant of anti-windup compensation |
| Derivative block | |||
| Real | Nd | 10 | The higher Nd, the more ideal the derivative block |
| Initialization | |||
| Real | xi_start | 0 | Initial value of integrator state |
| Real | yd_start | 0 | Initial value of derivative output |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u_s | Connector of setpoint input signal |
| input RealInput | u_m | Connector of measurement input signal |
| output RealOutput | y | Connector of actuator output signal |
| input BooleanInput | trigger | Resets the controller output when trigger becomes true |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Product
Buildings.Controls.OBC.CDL.Continuous.Product
Output product of the two inputs

Information
Block that outputs y = u1 * u2,
where
u1 and u2 are inputs.
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u1 | Connector of Real input signal 1 |
| input RealInput | u2 | Connector of Real input signal 2 |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Round
Buildings.Controls.OBC.CDL.Continuous.Round
Round real number to given digits

Information
Block that outputs the input after rounding it to n digits.
For example,
-
set
n = 0to round to the nearest integer, -
set
n = 1to round to the next decimal point, and -
set
n = -1to round to the next multiple of ten.
Hence, the block outputs
y = floor(u*(10^n) + 0.5)/(10^n) for u > 0,
y = ceil(u*(10^n) - 0.5)/(10^n) for u < 0.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Integer | n | Number of digits being round to |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Connector of Real input signal |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Sin
Buildings.Controls.OBC.CDL.Continuous.Sin
Output the sine of the input

Information
Block that outputs y = sin(u),
where
u is an input.
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Connector of Real input signal |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.SlewRateLimiter
Buildings.Controls.OBC.CDL.Continuous.SlewRateLimiter
Limit the increase or decrease rate of input

Information
The block limits the rate of change of the input by a ramp.
This block computes a threshold for the rate of change between
input u and output y as
thr = (u-y)/Td, where Td > 0 is parameter.
The output y is computed as follows:
If thr < fallingSlewRate, then dy/dt = fallingSlewRate,
if thr > raisingSlewRate, then dy/dt = raisingSlewRate,
otherwise, dy/dt = thr.
Implementation
For the block to work with arbitrary inputs and in order to produce a differential output,
the input is numerically differentiated with derivative time constant Td.
Smaller time constant Td means nearer ideal derivative.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | raisingSlewRate | Speed with which to increase the output [1/s] | |
| Real | fallingSlewRate | -raisingSlewRate | Speed with which to decrease the output [1/s] |
| Real | Td | raisingSlewRate*10 | Derivative time constant [s] |
| Boolean | enable | true | Set to false to disable rate limiter |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Connector of Real input signal |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Sort
Buildings.Controls.OBC.CDL.Continuous.Sort
Sort elements of input vector in ascending or descending order

Information
Block that sorts the elements of the input signal u.
If the parameter ascending = true, then the output signal satisfies
yi <= yi+1 for all i ∈ {1, ..., n-1}.
Otherwise, it satisfies
yi >= yi+1 for all i ∈ {1, ..., n-1}.
This block may for example be used in a variable air volume flow controller to access the position of the dampers that are most open.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Boolean | ascending | true | = true if ascending order, otherwise descending order |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u[nin] | Connector of Real input signals |
| output RealOutput | y[nin] | Connector of Real output signals |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Sqrt
Buildings.Controls.OBC.CDL.Continuous.Sqrt
Output the square root of the input (input >= 0 required)

Information
Block that outputs square root of the input y = sqrt(u),
where u is an input. All elements of the input vector shall be non-negative.
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Connector of Real input signal |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Tan
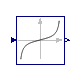
Buildings.Controls.OBC.CDL.Continuous.Tan
Output the tangent of the input

Information
Block that outputs y = tan(u),
where
u is an input.
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Connector of Real input signal |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Greater.GreaterWithHysteresis
Buildings.Controls.OBC.CDL.Continuous.Greater.GreaterWithHysteresis
Greater block without hysteresis

Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | h | 0 | Hysteresis |
| Advanced | |||
| Boolean | pre_y_start | false | Value of pre(y) at initial time |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u1 | Input u1 |
| input RealInput | u2 | Input u2 |
| output BooleanOutput | y | Output y |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Greater.GreaterNoHysteresis
Buildings.Controls.OBC.CDL.Continuous.Greater.GreaterNoHysteresis
Greater block without hysteresis

Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u1 | Input u1 |
| input RealInput | u2 | Input u2 |
| output BooleanOutput | y | Output y |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.GreaterThreshold.GreaterWithHysteresis
Buildings.Controls.OBC.CDL.Continuous.GreaterThreshold.GreaterWithHysteresis
Greater block without hysteresis

Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | t | 0 | Threshold for comparison |
| Real | h | 0 | Hysteresis |
| Advanced | |||
| Boolean | pre_y_start | false | Value of pre(y) at initial time |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Input u |
| output BooleanOutput | y | Output y |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.GreaterThreshold.GreaterNoHysteresis
Buildings.Controls.OBC.CDL.Continuous.GreaterThreshold.GreaterNoHysteresis
Greater block without hysteresis

Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | t | 0 | Threshold for comparison |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Input u |
| output BooleanOutput | y | Output y |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Less.LessWithHysteresis
Buildings.Controls.OBC.CDL.Continuous.Less.LessWithHysteresis
Less block without hysteresis

Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | h | 0 | Hysteresis |
| Advanced | |||
| Boolean | pre_y_start | false | Value of pre(y) at initial time |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u1 | Input u1 |
| input RealInput | u2 | Input u2 |
| output BooleanOutput | y | Output y |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.Less.LessNoHysteresis
Buildings.Controls.OBC.CDL.Continuous.Less.LessNoHysteresis
Less block without hysteresis

Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u1 | Input u1 |
| input RealInput | u2 | Input u2 |
| output BooleanOutput | y | Output y |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.LessThreshold.LessWithHysteresis
Buildings.Controls.OBC.CDL.Continuous.LessThreshold.LessWithHysteresis
Less block without hysteresis

Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | t | 0 | Threshold for comparison |
| Real | h | 0 | Hysteresis |
| Advanced | |||
| Boolean | pre_y_start | false | Value of pre(y) at initial time |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Input u |
| output BooleanOutput | y | Output y |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.LessThreshold.LessNoHysteresis
Buildings.Controls.OBC.CDL.Continuous.LessThreshold.LessNoHysteresis
Less block without hysteresis

Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | t | 0 | Threshold for comparison |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Input u |
| output BooleanOutput | y | Output y |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.PID.Derivative
Buildings.Controls.OBC.CDL.Continuous.PID.Derivative
Block that approximates the derivative of the input

Information
This blocks defines the transfer function between the
input u and the output y
as approximated derivative:
k * s
y = ------------ * u
T * s + 1
If k=0, the block reduces to y=0.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | k | 1 | Gains [1] |
| Real | T | 0.01 | Time constant (T>0 required) [s] |
| Initialization | |||
| Real | y_start | 0 | Initial value of output (= state) |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Connector of Real input signal |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
 Buildings.Controls.OBC.CDL.Continuous.PIDWithReset.Derivative
Buildings.Controls.OBC.CDL.Continuous.PIDWithReset.Derivative
Block that approximates the derivative of the input

Information
This blocks defines the transfer function between the
input u and the output y
as approximated derivative:
k * s
y = ------------ * u
T * s + 1
If k=0, the block reduces to y=0.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | k | 1 | Gains [1] |
| Real | T | 0.01 | Time constant (T>0 required) [s] |
| Initialization | |||
| Real | y_start | 0 | Initial value of output (= state) |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Connector of Real input signal |
| output RealOutput | y | Connector of Real output signal |
