Buildings.Fluid.HeatExchangers.DXCoils.AirCooled.Validation
Collection of validation models
Information
This package contains validation models for the classes in Buildings.Fluid.HeatExchangers.DXCoils.AirCooled.
Note that most validation models contain simple input data which may not be realistic, but for which the correct output can be obtained through an analytic solution. The examples plot various outputs, which have been verified against these solutions. These model outputs are stored as reference data and used for continuous validation whenever models in the library change.
Extends from Modelica.Icons.ExamplesPackage (Icon for packages containing runnable examples).
Package Content
| Name | Description |
|---|---|
 SingleSpeedEnergyPlus
|
Validation model for single speed DX coil with PLR=1 |
| SingleSpeedPLREnergyPlus
|
Validation model for single speed DX coil with PLR=1 |
Buildings.Fluid.HeatExchangers.DXCoils.AirCooled.Validation.SingleSpeedEnergyPlus
Validation model for single speed DX coil with PLR=1
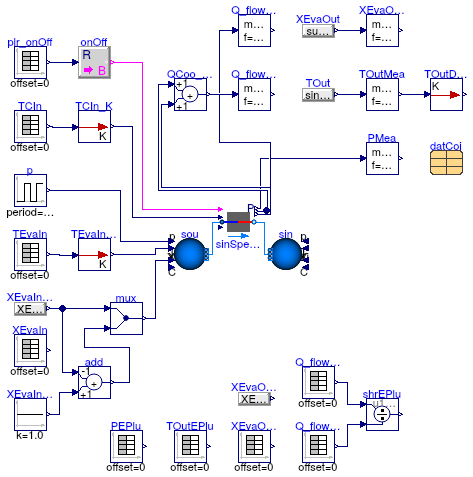
Information
This model validates the model Buildings.Fluid.HeatExchangers.DXCoils.AirCooled.SingleSpeed.
The difference in results of TOut and XOut at the beginning and end of the simulation is because the mass flow rate is zero. For zero mass flow rate, EnergyPlus assumes steady state condition, whereas the Modelica model is a dynamic model and hence the properties at the outlet are equal to the state variables of the model.
The EnergyPlus results were generated using the example file DXCoilSystemAuto.idf
from EnergyPlus 7.1,
with a nominal cooling capacity of 10500 Watts instead of using
autosizing. This allowed to have a part load ratio of one.
Note that EnergyPlus mass fractions (X) are in mass of water vapor per mass of dry air,
whereas Modelica uses the total mass as a reference. Hence, the EnergyPlus values
are corrected by dividing them by
1+X.
Extends from Modelica.Icons.Example (Icon for runnable examples).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Power | Q_flow_nominal | datCoi.sta[1].nomVal.Q_flow_... | Nominal power [W] |
| MassFlowRate | m_flow_nominal | datCoi.sta[1].nomVal.m_flow_... | Nominal mass flow rate [kg/s] |
| PressureDifference | dp_nominal | 1141 | Pressure drop at m_flow_nominal [Pa] |
Modelica definition
model SingleSpeedEnergyPlus
"Validation model for single speed DX coil with PLR=1"
extends Modelica.Icons.Example;
package Medium = Buildings.Media.Air "Medium model";
parameter Modelica.SIunits.Power Q_flow_nominal = datCoi.sta[1].nomVal.Q_flow_nominal
"Nominal power";
parameter Modelica.SIunits.MassFlowRate m_flow_nominal = datCoi.sta[1].nomVal.m_flow_nominal
"Nominal mass flow rate";
parameter Modelica.SIunits.PressureDifference dp_nominal = 1141
"Pressure drop at m_flow_nominal";
Buildings.Fluid.Sources.Boundary_pT sin(
redeclare package Medium = Medium,
p(displayUnit="Pa") = 101325,
nPorts=1,
T=303.15) "Sink";
Buildings.Fluid.Sources.Boundary_pT sou(
redeclare package Medium = Medium,
p(displayUnit="Pa") = 101325 + dp_nominal,
use_T_in=true,
nPorts=1,
use_p_in=true,
use_X_in=true,
T=299.85) "Source";
Buildings.Fluid.HeatExchangers.DXCoils.AirCooled.SingleSpeed sinSpeDX(
redeclare package Medium = Medium,
dp_nominal=dp_nominal,
datCoi=datCoi,
T_start=datCoi.sta[1].nomVal.TEvaIn_nominal,
from_dp=true,
energyDynamics=Modelica.Fluid.Types.Dynamics.FixedInitial)
"Single speed DX coil";
Buildings.Fluid.HeatExchangers.DXCoils.AirCooled.Data.Generic.DXCoil datCoi(
nSta=1, sta={Data.Generic.BaseClasses.Stage(
spe=1800/60,
nomVal=Data.Generic.BaseClasses.NominalValues(
Q_flow_nominal=-10500,
COP_nominal=3,
SHR_nominal=0.798655,
m_flow_nominal=1.72),
perCur=Examples.PerformanceCurves.Curve_II())}) "Coil data";
Modelica.Blocks.Sources.TimeTable plr_onOff(table=[0,0; 3600,0; 3600,0; 7200,0;
7200,0; 10800,0; 10800,0; 14400,0; 14400,0; 18000,0; 18000,0; 21600,0; 21600,
0; 25200,0; 25200,1; 28800,1; 28800,1; 32400,1; 32400,1; 36000,1; 36000,
1; 39600,1; 39600,1; 43200,1; 43200,1; 46800,1; 46800,1; 50400,1; 50400,
1; 54000,1; 54000,1; 57600,1; 57600,1; 61200,1; 61200,0; 64800,0; 64800,
0; 68400,0; 68400,0; 72000,0; 72000,0; 75600,0; 75600,0; 79200,0; 79200,
0; 82800,0; 82800,0; 86400,0])
"EnergyPlus PLR converted into on-off signal for this model";
Modelica.Blocks.Sources.TimeTable TCIn(table=[0,21.1; 3600,21.1; 3600,
20.80833333; 7200,20.80833333; 7200,20.89166667; 10800,20.89166667;
10800,21.1; 14400,21.1; 14400,20.80833333; 18000,20.80833333; 18000,
20.6; 21600,20.6; 21600,20.89166667; 25200,20.89166667; 25200,21.45;
28800,21.45; 28800,22.63333333; 32400,22.63333333; 32400,23.3; 36000,
23.3; 36000,25.575; 39600,25.575; 39600,28.19166667; 43200,28.19166667;
43200,27.90833333; 46800,27.90833333; 46800,26.90833333; 50400,
26.90833333; 50400,26.7; 54000,26.7; 54000,26.05833333; 57600,
26.05833333; 57600,24.60833333; 61200,24.60833333; 61200,23.55; 64800,
23.55; 64800,23.3; 68400,23.3; 68400,23.00833333; 72000,23.00833333;
72000,22.8; 75600,22.8; 75600,22.15833333; 79200,22.15833333; 79200,
21.35; 82800,21.35; 82800,21.1; 86400,21.1])
"Condenser inlet temperature";
Modelica.Blocks.Sources.TimeTable TEvaIn(table=[0,31.29534707; 3600,31.29534707;
3600,30.89999423; 7200,30.89999423; 7200,30.58355581; 10800,30.58355581;
10800,30.30108174; 14400,30.30108174; 14400,30.01393253; 18000,30.01393253;
18000,29.75672215; 21600,29.75672215; 21600,29.66076742; 25200,29.66076742;
25200,25.29138892; 28800,25.29138892; 28800,25.91180176; 32400,25.91180176;
32400,26.79831523; 36000,26.79831523; 36000,27.40611604; 39600,27.40611604;
39600,28.22402981; 43200,28.22402981; 43200,28.69183674; 46800,28.69183674;
46800,29.0211012; 50400,29.0211012; 50400,29.3698004; 54000,29.3698004;
54000,29.52289127; 57600,29.52289127; 57600,29.41955159; 61200,29.41955159;
61200,38.68278429; 64800,38.68278429; 64800,35.75595795; 68400,35.75595795;
68400,33.29770237; 72000,33.29770237; 72000,32.78839302; 75600,32.78839302;
75600,32.3989099; 79200,32.3989099; 79200,32.00270417; 82800,32.00270417;
82800,31.66453096; 86400,31.66453096]) "Coil inlet temperature";
Modelica.Blocks.Sources.TimeTable XEvaIn(table=[0,0.010526598; 3600,0.010526598;
3600,0.010526598; 7200,0.010526598; 7200,0.010526598; 10800,0.010526598;
10800,0.010526598; 14400,0.010526598; 14400,0.010526598; 18000,
0.010526598; 18000,0.010526598; 21600,0.010526598; 21600,0.010631087;
25200,0.010631087; 25200,0.010396485; 28800,0.010396485; 28800,
0.009496633; 32400,0.009496633; 32400,0.009521406; 36000,0.009521406;
36000,0.009576525; 39600,0.009576525; 39600,0.009574467; 43200,
0.009574467; 43200,0.009610872; 46800,0.009610872; 46800,0.009792709;
50400,0.009792709; 50400,0.010022684; 54000,0.010022684; 54000,
0.010213791; 57600,0.010213791; 57600,0.010384401; 61200,0.010384401;
61200,0.010396282; 64800,0.010396282; 64800,0.010537993; 68400,
0.010537993; 68400,0.010537961; 72000,0.010537961; 72000,0.010537961;
75600,0.010537961; 75600,0.010537961; 79200,0.010537961; 79200,
0.010537961; 82800,0.010537961; 82800,0.010537961; 86400,0.010537961])
"Water fraction of moist air";
Modelica.Blocks.Math.RealToBoolean onOff;
Modelica.Blocks.Routing.Multiplex2 mux "Converts in an array";
Buildings.Utilities.IO.BCVTB.From_degC TCIn_K "Converts degC to K";
Buildings.Utilities.IO.BCVTB.From_degC TEvaIn_K "Converts degC to K";
Modelica.Blocks.Math.Mean TOutMea(f=1/3600);
Buildings.Utilities.IO.BCVTB.To_degC TOutDegC;
Modelica.Blocks.Sources.RealExpression TOut(y=sinSpeDX.vol.T);
Modelica.Blocks.Math.Mean XEvaOutMea(f=1/3600);
Modelica.Blocks.Sources.RealExpression XEvaOut(y=sum(sinSpeDX.vol.Xi));
Modelica.Blocks.Math.Mean Q_flowMea(f=1/3600) "Mean of cooling rate";
Modelica.Blocks.Math.Mean Q_flowSenMea(f=1/3600)
"Mean of sensible cooling rate";
Modelica.Blocks.Math.Mean PMea(f=1/3600) "Mean of power";
Modelica.Blocks.Math.Add add(k1=-1);
Modelica.Blocks.Sources.Constant XEvaInMoiAir(k=1.0) "Moist air fraction = 1";
Modelica.Blocks.Sources.TimeTable TOutEPlu(table=[0,31.29534707; 3600,31.29534707;
3600,30.89999423; 7200,30.89999423; 7200,30.58355581; 10800,30.58355581;
10800,30.30108174; 14400,30.30108174; 14400,30.01393253; 18000,30.01393253;
18000,29.75672215; 21600,29.75672215; 21600,29.66076742; 25200,29.66076742;
25200,20.31734137; 28800,20.31734137; 28800,20.48740189; 32400,20.48740189;
32400,21.17362815; 36000,21.17362815; 36000,21.67091874; 39600,21.67091874;
39600,22.31588652; 43200,22.31588652; 43200,22.67802681; 46800,22.67802681;
46800,22.97615397; 50400,22.97615397; 50400,23.31283949; 54000,23.31283949;
54000,23.48357346; 57600,23.48357346; 57600,23.44857837; 61200,23.44857837;
61200,38.68278429; 64800,38.68278429; 64800,35.75595795; 68400,35.75595795;
68400,33.29770237; 72000,33.29770237; 72000,32.78839302; 75600,32.78839302;
75600,32.3989099; 79200,32.3989099; 79200,32.00270417; 82800,32.00270417;
82800,31.66453096; 86400,31.66453096])
"EnergyPlus result: outlet temperature";
Modelica.Blocks.Sources.TimeTable Q_flowEPlu(table=[0,-1e-07; 3600,-1e-07; 3600,
-1e-07; 7200,-1e-07; 7200,-1e-07; 10800,-1e-07; 10800,-1e-07; 14400,-1e-07;
14400,-1e-07; 18000,-1e-07; 18000,-1e-07; 21600,-1e-07; 21600,-1e-07; 25200,
-1e-07; 25200,-10983.1144101; 28800,-10983.1144101; 28800,-10855.9768001;
32400,-10855.9768001; 32400,-10903.5304201; 36000,-10903.5304201; 36000,
-10877.5678501; 39600,-10877.5678501; 39600,-10822.2172001; 43200,-10822.2172001;
43200,-10878.2459001; 46800,-10878.2459001; 46800,-10981.5365901; 50400,
-10981.5365901; 50400,-11055.6112701; 54000,-11055.6112701; 54000,-11121.6278701;
57600,-11121.6278701; 57600,-11185.7466001; 61200,-11185.7466001; 61200,
-1e-07; 64800,-1e-07; 64800,-1e-07; 68400,-1e-07; 68400,-1e-07; 72000,-1e-07;
72000,-1e-07; 75600,-1e-07; 75600,-1e-07; 79200,-1e-07; 79200,-1e-07; 82800,
-1e-07; 82800,-1e-07; 86400,-1e-07]) "EnergyPlus result: heat flow";
Modelica.Blocks.Sources.TimeTable Q_flowSenEPlu(table=[0,0; 3600,0; 3600,0; 7200,
0; 7200,0; 10800,0; 10800,0; 14400,0; 14400,0; 18000,0; 18000,0; 21600,0;
21600,0; 25200,0; 25200,-8537.795206; 28800,-8537.795206; 28800,-9298.755552;
32400,-9298.755552; 32400,-9643.742602; 36000,-9643.742602; 36000,-9835.115234;
39600,-9835.115234; 39600,-10133.17939; 43200,-10133.17939; 43200,-10315.64445;
46800,-10315.64445; 46800,-10372.27848; 50400,-10372.27848; 50400,-10397.02013;
54000,-10397.02013; 54000,-10369.92204; 57600,-10369.92204; 57600,-10254.97156;
61200,-10254.97156; 61200,0; 64800,0; 64800,0; 68400,0; 68400,0; 72000,0;
72000,0; 75600,0; 75600,0; 79200,0; 79200,0; 82800,0; 82800,0; 86400,0])
"EnergyPlus result: sensible heat flow ";
Modelica.Blocks.Math.Division shrEPlu "EnergyPlus result: SHR";
Modelica.Blocks.Sources.TimeTable XEvaOutEPlu(table=[0,0.010526598; 3600,0.010526598;
3600,0.010526598; 7200,0.010526598; 7200,0.010526598; 10800,0.010526598;
10800,0.010526598; 14400,0.010526598; 14400,0.010526598; 18000,0.010526598;
18000,0.010526598; 21600,0.010526598; 21600,0.010631087; 25200,0.010631087;
25200,0.009824324; 28800,0.009824324; 28800,0.009132468; 32400,0.009132468;
32400,0.009227012; 36000,0.009227012; 36000,0.009333022; 39600,0.009333022;
39600,0.009413613; 43200,0.009413613; 43200,0.009479582; 46800,0.009479582;
46800,0.009650565; 50400,0.009650565; 50400,0.009869069; 54000,0.009869069;
54000,0.010038477; 57600,0.010038477; 57600,0.010167307; 61200,0.010167307;
61200,0.010396282; 64800,0.010396282; 64800,0.010537993; 68400,0.010537993;
68400,0.010537961; 72000,0.010537961; 72000,0.010537961; 75600,0.010537961;
75600,0.010537961; 79200,0.010537961; 79200,0.010537961; 82800,0.010537961;
82800,0.010537961; 86400,0.010537961])
"EnergyPlus result: outlet water mass fraction";
Modelica.Blocks.Sources.TimeTable PEPlu(table=[0,0; 3600,0; 3600,0; 7200,0; 7200,
0; 10800,0; 10800,0; 14400,0; 14400,0; 18000,0; 18000,0; 21600,0; 21600,
0; 25200,0; 25200,2947.546668; 28800,2947.546668; 28800,2966.686535; 32400,
2966.686535; 32400,2999.864072; 36000,2999.864072; 36000,3087.801241; 39600,
3087.801241; 39600,3195.082124; 43200,3195.082124; 43200,3188.668029; 46800,
3188.668029; 46800,3156.065892; 50400,3156.065892; 50400,3155.199826; 54000,
3155.199826; 54000,3136.04256; 57600,3136.04256; 57600,3087.770321; 61200,
3087.770321; 61200,0; 64800,0; 64800,0; 68400,0; 68400,0; 72000,0; 72000,
0; 75600,0; 75600,0; 79200,0; 79200,0; 82800,0; 82800,0; 86400,0])
"EnergyPlus result: electric power";
Modelica.Blocks.Sources.Pulse p(
nperiod=1,
offset=101325,
amplitude=1141,
width=100,
period=36000,
startTime=25200) "Pressure";
Modelica.Blocks.Sources.RealExpression XEvaInMod(y=XEvaIn.y/(1 + XEvaIn.y))
"Modified XEvaIn";
Modelica.Blocks.Sources.RealExpression XEvaOutEPluMod(y=XEvaOutEPlu.y/(1 + XEvaOutEPlu.y))
"Modified XEvaOut of energyPlus to comapre with the model results";
Modelica.Blocks.Math.Add QCoo_flow "Total cooling heat flow rate";
equation
connect(sou.ports[1], sinSpeDX.port_a);
connect(sinSpeDX.port_b, sin.ports[1]);
connect(plr_onOff.y, onOff.u);
connect(onOff.y, sinSpeDX.on);
connect(mux.y, sou.X_in);
connect(TCIn.y, TCIn_K.Celsius);
connect(TCIn_K.Kelvin, sinSpeDX.TConIn);
connect(TEvaIn.y, TEvaIn_K.Celsius);
connect(TEvaIn_K.Kelvin, sou.T_in);
connect(TOut.y, TOutMea.u);
connect(TOutMea.y, TOutDegC.Kelvin);
connect(XEvaOut.y, XEvaOutMea.u);
connect(XEvaInMoiAir.y, add.u2);
connect(add.y, mux.u2[1]);
connect(Q_flowSenEPlu.y, shrEPlu.u1);
connect(Q_flowEPlu.y, shrEPlu.u2);
connect(sinSpeDX.P, PMea.u);
connect(p.y, sou.p_in);
connect(XEvaInMod.y, mux.u1[1]);
connect(XEvaInMod.y, add.u1);
connect(sinSpeDX.QSen_flow, Q_flowSenMea.u);
connect(QCoo_flow.y, Q_flowMea.u);
connect(QCoo_flow.u1, sinSpeDX.QSen_flow);
connect(sinSpeDX.QLat_flow, QCoo_flow.u2);
end SingleSpeedEnergyPlus;
Buildings.Fluid.HeatExchangers.DXCoils.AirCooled.Validation.SingleSpeedPLREnergyPlus
Validation model for single speed DX coil with PLR=1
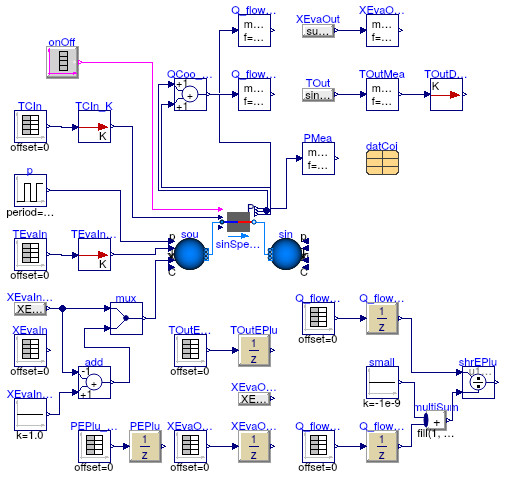
Information
This model validates the model Buildings.Fluid.HeatExchangers.DXCoils.AirCooled.SingleSpeed.
The difference in results of TOut and XOut at the beginning and end of the simulation is because the mass flow rate is zero. For zero mass flow rate, EnergyPlus assumes steady state condition, whereas the Modelica model is a dynamic model and hence the properties at the outlet are equal to the state variables of the model.
The EnergyPlus results were generated using the example file DXCoilSystemAuto.idf
from EnergyPlus 7.1.
The EnergyPlus results were generated using the example file
DXCoilSystemAuto.idf from EnergyPlus 7.1.
On the summer design day, the PLR is below 1.
A similar effect has been achieved in this example by turning on the coil only for the period
during which it run in EnergyPlus.
This results in on-off cycle and fluctuating results.
To compare the results, the Modelica outputs are averaged over 3600 seconds,
and the EnergyPlus outputs are used with a zero order delay to avoid the time shift in results.
Note that EnergyPlus mass fractions (X) are in mass of water vapor per mass of dry air,
whereas Modelica uses the total mass as a reference. Hence, the EnergyPlus values
are corrected by dividing them by
1+X.
Extends from Modelica.Icons.Example (Icon for runnable examples).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Power | Q_flow_nominal | datCoi.sta[1].nomVal.Q_flow_... | Nominal power [W] |
| MassFlowRate | m_flow_nominal | datCoi.sta[1].nomVal.m_flow_... | Nominal mass flow rate [kg/s] |
| PressureDifference | dp_nominal | 1141 | Pressure drop at m_flow_nominal [Pa] |
Modelica definition
model SingleSpeedPLREnergyPlus
"Validation model for single speed DX coil with PLR=1"
extends Modelica.Icons.Example;
package Medium = Buildings.Media.Air "Medium model";
parameter Modelica.SIunits.Power Q_flow_nominal = datCoi.sta[1].nomVal.Q_flow_nominal
"Nominal power";
parameter Modelica.SIunits.MassFlowRate m_flow_nominal = datCoi.sta[1].nomVal.m_flow_nominal
"Nominal mass flow rate";
parameter Modelica.SIunits.PressureDifference dp_nominal = 1141
"Pressure drop at m_flow_nominal";
Buildings.Fluid.Sources.Boundary_pT sin(
redeclare package Medium = Medium,
p(displayUnit="Pa") = 101325,
nPorts=1,
T=303.15) "Sink";
Buildings.Fluid.Sources.Boundary_pT sou(
redeclare package Medium = Medium,
p(displayUnit="Pa") = 101325 + dp_nominal,
use_T_in=true,
nPorts=1,
use_p_in=true,
use_X_in=true,
T=299.85) "Source";
Buildings.Fluid.HeatExchangers.DXCoils.AirCooled.SingleSpeed sinSpeDX(
redeclare package Medium = Medium,
dp_nominal=dp_nominal,
datCoi=datCoi,
T_start=datCoi.sta[1].nomVal.TEvaIn_nominal,
from_dp=true,
computeReevaporation=true,
eva(m(start=0)),
energyDynamics=Modelica.Fluid.Types.Dynamics.FixedInitial)
"Single speed DX coil";
Modelica.Blocks.Routing.Multiplex2 mux "Converts in an array";
Buildings.Utilities.IO.BCVTB.From_degC TCIn_K "Converts degC to K";
Buildings.Utilities.IO.BCVTB.From_degC TEvaIn_K "Converts degC to K";
Modelica.Blocks.Math.Mean TOutMea(f=1/3600);
Buildings.Utilities.IO.BCVTB.To_degC TOutDegC;
Modelica.Blocks.Sources.RealExpression TOut(y=sinSpeDX.vol.T);
Modelica.Blocks.Math.Mean XEvaOutMea(f=1/3600);
Modelica.Blocks.Sources.RealExpression XEvaOut(y=sum(sinSpeDX.vol.Xi));
Modelica.Blocks.Math.Mean Q_flowMea(f=1/3600) "Mean of cooling rate";
Modelica.Blocks.Math.Mean Q_flowSenMea(f=1/3600)
"Mean of sensible cooling rate";
Modelica.Blocks.Math.Mean PMea(f=1/3600) "Mean of power";
Modelica.Blocks.Math.Add add(k1=-1);
Modelica.Blocks.Sources.Constant XEvaInMoiAir(k=1.0) "Moist air fraction = 1";
Modelica.Blocks.Math.Division shrEPlu "EnergyPlus result: SHR";
Modelica.Blocks.Sources.Pulse p(
nperiod=1,
offset=101325,
width=100,
period=36000,
startTime=25200,
amplitude=1086) "Pressure";
Modelica.Blocks.Sources.RealExpression XEvaInMod(y=XEvaIn.y/(1 + XEvaIn.y))
"Modified XEvaIn";
Modelica.Blocks.Sources.RealExpression XEvaOutEPluMod(y=XEvaOutEPlu.y/(1 + XEvaOutEPlu.y))
"Modified XEvaOut of energyPlus to comapre with the model results";
Modelica.Blocks.Sources.BooleanTable onOff(startValue=true, table={
0,
25200,
26223.8694421458,
28800,
30457.5364262964,
32400,
34157.5093643325,
36000,
37915.2504828207,
39600,
41687.2390146012,
43200,
45363.3505825759,
46800,
49129.0477925565,
50400,
52764.5288886473,
54000,
56361.5689116996,
57600,
59868.3223307805}) "EnergyPlus PLR converted into on-off signal for this model";
Modelica.Blocks.Sources.TimeTable TCIn(table=[0,21.1; 3600,21.1; 3600,
20.80833333; 7200,20.80833333; 7200,20.89166667; 10800,20.89166667;
10800,21.1; 14400,21.1; 14400,20.80833333; 18000,20.80833333; 18000,
20.6; 21600,20.6; 21600,20.89166667; 25200,20.89166667; 25200,21.45;
28800,21.45; 28800,22.63333333; 32400,22.63333333; 32400,23.3; 36000,
23.3; 36000,25.575; 39600,25.575; 39600,28.19166667; 43200,28.19166667;
43200,27.90833333; 46800,27.90833333; 46800,26.90833333; 50400,
26.90833333; 50400,26.7; 54000,26.7; 54000,26.05833333; 57600,
26.05833333; 57600,24.60833333; 61200,24.60833333; 61200,23.55; 64800,
23.55; 64800,23.3; 68400,23.3; 68400,23.00833333; 72000,23.00833333;
72000,22.8; 75600,22.8; 75600,22.15833333; 79200,22.15833333; 79200,
21.35; 82800,21.35; 82800,21.1; 86400,21.1])
"Condenser inlet temperature";
Modelica.Blocks.Sources.TimeTable TEvaIn(table=[
0,29.34948133;
3600,29.34948133;
3600,29.01814876;
7200,29.01814876;
7200,28.76345897;
10800,28.76345897;
10800,28.53396626;
14400,28.53396626;
14400,28.29506697;
18000,28.29506697;
18000,28.08827214;
21600,28.08827214;
21600,28.04639166;
25200,28.04639166;
25200,24.08651629;
28800,24.08651629;
28800,24.09243025;
32400,24.09243025;
32400,24.20516777;
36000,24.20516777;
36000,24.37566383;
39600,24.37566383;
39600,24.56160617;
43200,24.56160617;
43200,24.52393669;
46800,24.52393669;
46800,24.39077471;
50400,24.39077471;
50400,24.33155125;
54000,24.33155125;
54000,24.27362306;
57600,24.27362306;
57600,24.16566121;
61200,24.16566121;
61200,35.62393274;
64800,35.62393274;
64800,32.89683519;
68400,32.89683519;
68400,31.14979083;
72000,31.14979083;
72000,30.65928154;
75600,30.65928154;
75600,30.28912721;
79200,30.28912721;
79200,29.91867206;
82800,29.91867206;
82800,29.61490681;
86400,29.61490681]) "Coil inlet temperature";
Modelica.Blocks.Sources.TimeTable XEvaIn(table=[
0,0.00946;
3600,0.00946;
3600,0.00946;
7200,0.00946;
7200,0.00946;
10800,0.00946;
10800,0.00946;
14400,0.00946;
14400,0.00946;
18000,0.00946;
18000,0.00946;
21600,0.00946;
21600,0.00955;
25200,0.00955;
25200,0.0103;
28800,0.0103;
28800,0.0109;
32400,0.0109;
32400,0.0108;
36000,0.0108;
36000,0.0105;
39600,0.0105;
39600,0.01;
43200,0.01;
43200,0.00969;
46800,0.00969;
46800,0.00947;
50400,0.00947;
50400,0.00926;
54000,0.00926;
54000,0.00923;
57600,0.00923;
57600,0.00937;
61200,0.00937;
61200,0.00936;
64800,0.00936;
64800,0.00946;
68400,0.00946;
68400,0.00946;
72000,0.00946;
72000,0.00946;
75600,0.00946;
75600,0.00946;
79200,0.00946;
79200,0.00946;
82800,0.00946;
82800,0.00946;
86400,0.00946]) "Water fraction of moist air";
Modelica.Blocks.Sources.TimeTable TOutEPlu_ori(table=[0,29.34948133; 3600,29.34948133;
3600,29.01814876; 7200,29.01814876; 7200,28.76345897; 10800,28.76345897;
10800,28.53396626; 14400,28.53396626; 14400,28.29506697; 18000,28.29506697;
18000,28.08827214; 21600,28.08827214; 21600,28.04639166; 25200,28.04639166;
25200,19.79102221; 28800,19.79102221; 28800,17.58304653; 32400,17.58304653;
32400,17.35471965; 36000,17.35471965; 36000,16.95320861; 39600,16.95320861;
39600,16.4388043; 43200,16.4388043; 43200,16.03301122; 46800,16.03301122;
46800,15.41071946; 50400,15.41071946; 50400,15.15437515; 54000,15.15437515;
54000,15.09543443; 57600,15.09543443; 57600,15.3159498; 61200,15.3159498;
61200,35.62393274; 64800,35.62393274; 64800,32.89683519; 68400,32.89683519;
68400,31.14979083; 72000,31.14979083; 72000,30.65928154; 75600,30.65928154;
75600,30.28912721; 79200,30.28912721; 79200,29.91867206; 82800,29.91867206;
82800,29.61490681; 86400,29.61490681])
"EnergyPlus result: outlet temperature";
Modelica.Blocks.Sources.TimeTable PEPlu_ori(table=[0,0; 3600,0; 3600,0; 7200,
0; 7200,0; 10800,0; 10800,0; 14400,0; 14400,0; 18000,0; 18000,0; 21600,
0; 21600,0; 25200,0; 25200,2221.47212; 28800,2221.47212; 28800,
3595.947729; 32400,3595.947729; 32400,3819.11052; 36000,3819.11052;
36000,4235.566014; 39600,4235.566014; 39600,4714.070326; 43200,
4714.070326; 43200,4835.805362; 46800,4835.805362; 46800,5089.357992;
50400,5089.357992; 50400,5132.912713; 54000,5132.912713; 54000,
5082.720823; 57600,5082.720823; 57600,4820.015593; 61200,4820.015593;
61200,0; 64800,0; 64800,0; 68400,0; 68400,0; 72000,0; 72000,0; 75600,0;
75600,0; 79200,0; 79200,0; 82800,0; 82800,0; 86400,0])
"EnergyPlus result: electric power";
Modelica.Blocks.Sources.TimeTable XEvaOutEPlu_ori(table=[0,0.009460927; 3600,0.009460927;
3600,0.009460927; 7200,0.009460927; 7200,0.009460927; 10800,0.009460927;
10800,0.009460927; 14400,0.009460927; 14400,0.009460927; 18000,0.009460927;
18000,0.009460927; 21600,0.009460927; 21600,0.009553929; 25200,0.009553929;
25200,0.010316263; 28800,0.010316263; 28800,0.010677981; 32400,0.010677981;
32400,0.010521771; 36000,0.010521771; 36000,0.010225222; 39600,0.010225222;
39600,0.009821415; 43200,0.009821415; 43200,0.009523837; 46800,0.009523837;
46800,0.009220467; 50400,0.009220467; 50400,0.009042737; 54000,0.009042737;
54000,0.009012184; 57600,0.009012184; 57600,0.009145645; 61200,0.009145645;
61200,0.009361285; 64800,0.009361285; 64800,0.009459829; 68400,0.009459829;
68400,0.009459801; 72000,0.009459801; 72000,0.009459801; 75600,0.009459801;
75600,0.009459801; 79200,0.009459801; 79200,0.009459801; 82800,0.009459801;
82800,0.009459801; 86400,0.009459801])
"EnergyPlus result: outlet water mass fraction";
Modelica.Blocks.Sources.TimeTable Q_flowSenEPlu_ori(table=[0,0; 3600,0; 3600,0;
7200,0; 7200,0; 10800,0; 10800,0; 14400,0; 14400,0; 18000,0; 18000,0; 21600,
0; 21600,0; 25200,0; 25200,7378.442557; 28800,7378.442557; 28800,11190.03413;
32400,11190.03413; 32400,11772.99874; 36000,11772.99874; 36000,12749.11676;
39600,12749.11676; 39600,13941.844; 43200,13941.844; 43200,14565.84942;
46800,14565.84942; 46800,15396.44898; 50400,15396.44898; 50400,15729.34223;
54000,15729.34223; 54000,15730.20543; 57600,15730.20543; 57600,15170.91533;
61200,15170.91533; 61200,0; 64800,0; 64800,0; 68400,0; 68400,0; 72000,0;
72000,0; 75600,0; 75600,0; 79200,0; 79200,0; 82800,0; 82800,0; 86400,0])
"EnergyPlus result: sensible heat flow ";
Modelica.Blocks.Sources.TimeTable Q_flowEPlu_ori(table=[0,0; 3600,0; 3600,
0; 7200,0; 7200,0; 10800,0; 10800,0; 14400,0; 14400,
0; 18000,0; 18000,0; 21600,0; 21600,0; 25200,-1e-9;
25200,-7464.76568; 28800,-7464.76568; 28800,-12134.51902; 32400,-12134.51902;
32400,-12829.73888; 36000,-12829.73888; 36000,-13827.82263; 39600,-13827.82263;
39600,-14802.70071; 43200,-14802.70071; 43200,-15271.18519; 46800,-15271.18519;
46800,-16441.6341; 50400,-16441.6341; 50400,-16638.80981; 54000,-16638.80981;
54000,-16649.7802; 57600,-16649.7802; 57600,-16109.92984; 61200,-16109.92984;
61200,0; 64800,0; 64800,0; 68400,0; 68400,0; 72000,0;
72000,0; 75600,0; 75600,0; 79200,0; 79200,0; 82800,0;
82800,0; 86400,0]) "EnergyPlus result: heat flow";
Data.Generic.DXCoil datCoi(nSta=1, sta={Data.Generic.BaseClasses.Stage(
spe=1800/60,
nomVal=Data.Generic.BaseClasses.NominalValues(
Q_flow_nominal=-25237.66,
COP_nominal=3,
SHR_nominal=0.775047,
m_flow_nominal=1.72,
tWet=1000,
gamma=1.5),
perCur=Examples.PerformanceCurves.Curve_II())}) "Coil data";
Modelica.Blocks.Math.Add QCoo_flow "Total cooling heat flow rate";
UnitDelay PEPlu(samplePeriod=3600);
UnitDelay Q_flowSenEPlu(samplePeriod=3600);
UnitDelay Q_flowEPlu(samplePeriod=3600);
UnitDelay TOutEPlu(samplePeriod=3600, y_start=29.34948133);
UnitDelay XEvaOutEPlu(samplePeriod=3600);
Modelica.Blocks.Math.MultiSum multiSum(nu=2);
Modelica.Blocks.Sources.Constant small(k=-1e-9)
"Small value to avoid division by zero";
// The UnitDelay is reimplemented to avoid in Dymola 2016 the translation warning
// The initial conditions for variables of type Boolean are not fully specified.
// Dymola has selected default initial conditions.
// Assuming fixed default start value for the discrete non-states:
// PEPlu.firstTrigger(start = false)
// ...
protected
block UnitDelay
extends Modelica.Blocks.Discrete.UnitDelay(
firstTrigger(start=false, fixed=true));
end UnitDelay;
equation
connect(sou.ports[1], sinSpeDX.port_a);
connect(sinSpeDX.port_b, sin.ports[1]);
connect(mux.y, sou.X_in);
connect(TCIn_K.Kelvin, sinSpeDX.TConIn);
connect(TEvaIn_K.Kelvin, sou.T_in);
connect(TOut.y, TOutMea.u);
connect(TOutMea.y, TOutDegC.Kelvin);
connect(XEvaOut.y, XEvaOutMea.u);
connect(XEvaInMoiAir.y, add.u2);
connect(add.y, mux.u2[1]);
connect(sinSpeDX.P, PMea.u);
connect(p.y, sou.p_in);
connect(XEvaInMod.y, mux.u1[1]);
connect(XEvaInMod.y, add.u1);
connect(onOff.y, sinSpeDX.on);
connect(TCIn.y, TCIn_K.Celsius);
connect(TEvaIn.y, TEvaIn_K.Celsius);
connect(sinSpeDX.QSen_flow, Q_flowSenMea.u);
connect(QCoo_flow.y, Q_flowMea.u);
connect(QCoo_flow.u1, sinSpeDX.QSen_flow);
connect(sinSpeDX.QLat_flow, QCoo_flow.u2);
connect(PEPlu_ori.y, PEPlu.u);
connect(Q_flowSenEPlu_ori.y, Q_flowSenEPlu.u);
connect(Q_flowSenEPlu.y, shrEPlu.u1);
connect(Q_flowEPlu_ori.y, Q_flowEPlu.u);
connect(TOutEPlu_ori.y, TOutEPlu.u);
connect(XEvaOutEPlu_ori.y, XEvaOutEPlu.u);
connect(multiSum.y, shrEPlu.u2);
connect(small.y, multiSum.u[1]);
connect(Q_flowEPlu.y, multiSum.u[2]);
end SingleSpeedPLREnergyPlus;
Buildings.Fluid.HeatExchangers.DXCoils.AirCooled.Validation.SingleSpeedPLREnergyPlus.UnitDelay
Information
Extends from Modelica.Blocks.Discrete.UnitDelay (Unit Delay Block).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Real | y_start | 0 | Initial value of output signal |
| Time | samplePeriod | Sample period of component [s] | |
| Time | startTime | 0 | First sample time instant [s] |
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | u | Connector of Real input signal |
| output RealOutput | y | Connector of Real output signal |
Modelica definition
block UnitDelay
extends Modelica.Blocks.Discrete.UnitDelay(
firstTrigger(start=false, fixed=true));
end UnitDelay;