Buildings.Fluid.Geothermal.Borefields.BaseClasses.HeatTransfer
Package with ground heat transfer models
Information
This package contains models and functions to solve ground heat transfer around ground heat exchangers. For more information on the model implementation, see the documentation of Buildings.Fluid.Geothermal.Borefields.BaseClasses.HeatTransfer.GroundTemperatureResponse.
Extends from Modelica.Icons.VariantsPackage (Icon for package containing variants).
Package Content
| Name | Description |
|---|---|
| Heat conduction in a cylinder using the radial discretization as advised by Eskilson | |
| Model calculating discrete load aggregation | |
| Package with functions for load aggregation | |
| Models for heat transfer outside boreholes | |
| Validation models for GroundHeatTransfer |
 Buildings.Fluid.Geothermal.Borefields.BaseClasses.HeatTransfer.Cylindrical
Buildings.Fluid.Geothermal.Borefields.BaseClasses.HeatTransfer.Cylindrical
Heat conduction in a cylinder using the radial discretization as advised by Eskilson

Information
Model for radial heat transfer in a hollow cylinder.
If the heat capacity of the material is non-zero, then this model computes transient heat conduction, i.e., it computes a numerical approximation to the solution of the heat equation
ρ c ( ∂ T(r,t) ⁄ ∂t ) = k ( ∂² T(r,t) ⁄ ∂r² + 1 ⁄ r ∂ T(r,t) ⁄ ∂r ),
where ρ is the mass density, c is the specific heat capacity per unit mass, T is the temperature at location r and time t and k is the heat conductivity. At the locations r=ra and r=rb, the temperature and heat flow rate are equal to the temperature and heat flow rate of the heat ports.
If the heat capacity of the material is set to zero, then steady-state heat flow is computed using
Q = 2 π k (Ta-Tb)⁄ ln(ra ⁄ rb),
where ra is the internal radius, rb is the external radius, Ta is the temperature at port a and Tb is the temperature at port b.
Implementation
To spatially discretize the heat equation, the construction is
divided into compartments with nSta ≥ 1 state variables.
The state variables are connected to each other through thermal conductors.
There is also a thermal conductor
between the surfaces and the outermost state variables. Thus, to obtain
the surface temperature, use port_a.T (or port_b.T)
and not the variable T[1].
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Template | soiDat | ||
| Height | h | Height of the cylinder [m] | |
| Radius | r_a | Internal radius [m] | |
| Radius | r_b | External radius [m] | |
| Integer | nSta | 10 | Number of state variables |
| Real | gridFac | 2 | Grid factor for spacing |
| Radius | r[nSta + 1] | r( ... | Radius to the boundary of the i-th domain [m] |
| Initialization | |||
| Temperature | TInt_start | Initial temperature at port_a, used if steadyStateInitial = false [K] | |
| Temperature | TExt_start | Initial temperature at port_b, used if steadyStateInitial = false [K] | |
| Boolean | steadyStateInitial | false | true initializes dT(0)/dt=0, false initializes T(0) at fixed temperature using T_a_start and T_b_start |
Connectors
| Type | Name | Description |
|---|---|---|
| HeatPort_a | port_a | Heat port at surface a |
| HeatPort_b | port_b | Heat port at surface b |
Modelica definition
 Buildings.Fluid.Geothermal.Borefields.BaseClasses.HeatTransfer.GroundTemperatureResponse
Buildings.Fluid.Geothermal.Borefields.BaseClasses.HeatTransfer.GroundTemperatureResponse
Model calculating discrete load aggregation

Information
This model calculates the ground temperature response to obtain the temperature at the borehole wall in a geothermal system where heat is being injected into or extracted from the ground.
A load-aggregation scheme based on that developed by Claesson and Javed (2012) is
used to calculate the borehole wall temperature response with the temporal superposition
of ground thermal loads. In its base form, the
load-aggregation scheme uses fixed-length aggregation cells to agglomerate
thermal load history together, with more distant cells (denoted with a higher cell and vector index)
representing more distant thermal history. The more distant the thermal load, the
less impactful it is on the borehole wall temperature change at the current time step.
Each cell has an aggregation time associated to it denoted by nu,
which corresponds to the simulation time (since the beginning of heat injection or
extraction) at which the cell will begin shifting its thermal load to more distant
cells. To determine nu, cells have a temporal size rcel
(rcel in this model)
which follows the exponential growth
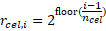
where nCel is the number of consecutive cells which can have the same size.
Decreasing rcel will generally decrease calculation times, at the cost of
precision in the temporal superposition. rcel is expressed in multiples
of the aggregation time resolution (via the parameter tLoaAgg).
Then, nu may be expressed as the sum of all rcel values
(multiplied by the aggregation time resolution) up to and including that cell in question.
To determine the weighting factors, the borefield's temperature step response at the borefield wall is determined as
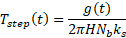
where g(·) is the borefield's thermal response factor known as the g-function,
H is the total length of all boreholes and ks is the thermal
conductivity of the soil. The weighting factors kappa (κ in the equation below)
for a given cell i are then expressed as follows.
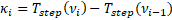
where ν refers to the vector nu in this model and
Tstep(ν0)=0.
At every aggregation time step, a time event is generated to perform the load aggregation steps. First, the thermal load is shifted. When shifting between cells of different size, total energy is conserved. This operation is illustred in the figure below by Cimmino (2014).
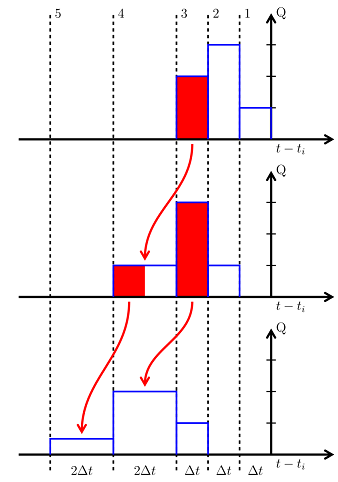
After the cell-shifting operation is performed, the first aggregation cell has its
value set to the average thermal load since the last aggregation step.
Temporal superposition is then applied by means
of a scalar product between the aggregated thermal loads QAgg_flow and the
weighting factors κ.
Due to Modelica's variable time steps, the load aggregation scheme is modified by separating the thermal response between the current aggregation time step and everything preceding it. This is done according to
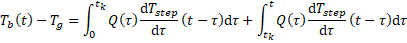
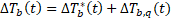
where Tb is the borehole wall temperature,
Tg
is the undisturbed ground temperature,
Q is the ground thermal load per borehole length and h = g/(2 π ks)
is a temperature response factor based on the g-function. tk
is the last discrete aggregation time step, meaning that the current time t
satisfies tk≤t≤tk+1.
Δtagg(=tk+1-tk) is the
parameter tLoaAgg in the present model.
Thus, ΔTb*(t) is the borehole wall temperature change due to the thermal history prior to the current aggregation step. At every aggregation time step, load aggregation and temporal superposition are used to calculate its discrete value. Assuming no heat injection or extraction until tk+1, this term is assumed to have a linear time derivative, which is given by the difference between ΔTb*(tk+1) (the temperature change from load history at the next discrete aggregation time step, which is constant over the duration of the ongoing aggregation time step) and the total temperature change at the last aggregation time step, ΔTb(t).
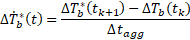
The second term ΔTb,q(t) concerns the ongoing aggregation time step.
To obtain the time derivative of this term, the thermal response factor h is assumed
to vary linearly over the course of an aggregation time step. Therefore, because
the ongoing aggregation time step always concerns the first aggregation cell, its derivative (denoted
by the parameter dTStepdt in this model) can be calculated as
kappa[1], the first value in the kappa vector,
divided by the aggregation time step Δt.
The derivative of the temperature change at the borehole wall is then expressed
as the multiplication of dTStepdt (which only needs to be
calculated once at the start of the simulation) and the heat flow Q at
the borehole wall.
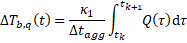
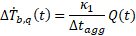
With the two terms in the expression of ΔTb(t) expressed
as time derivatives, ΔTb(t) can itself also be
expressed as its time derivative and implemented as such directly in the Modelica
equations block with the der() operator.
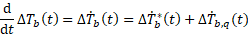
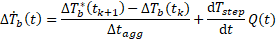
This load aggregation scheme is validated in Buildings.Fluid.Geothermal.Borefields.BaseClasses.HeatTransfer.Validation.Analytic_20Years.
References
Cimmino, M. 2014. Développement et validation expérimentale de facteurs de réponse thermique pour champs de puits géothermiques, Ph.D. Thesis, École Polytechnique de Montréal.
Claesson, J. and Javed, S. 2012. A load-aggregation method to calculate extraction temperatures of borehole heat exchangers. ASHRAE Transactions 118(1): 530-539.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Time | tLoaAgg | 3600 | Time resolution of load aggregation [s] |
| Integer | nCel | 5 | Number of cells per aggregation level |
| Boolean | forceGFunCalc | false | Set to true to force the thermal response to be calculated at the start instead of checking whether it has been pre-computed |
| Template | borFieDat | Record containing all the parameters of the borefield model |
Connectors
| Type | Name | Description |
|---|---|---|
| output RealOutput | delTBor | Temperature difference current borehole wall temperature minus initial borehole wall temperature [K] |
| input RealInput | QBor_flow | Heat flow from all boreholes combined (positive if heat from fluid into soil) [W] |
