Buildings.HeatTransfer.Conduction.BaseClasses.Examples
Collection of models that illustrate model use and test models
Information
This package contains examples for the use of models that can be found in Buildings.HeatTransfer.Conduction.BaseClasses.
Extends from Modelica.Icons.ExamplesPackage (Icon for packages containing runnable examples).
Package Content
| Name | Description |
|---|---|
 Temperature_u
|
Approximation of specific internal energy versus temperature curve with cubic hermite cubic spline |
Buildings.HeatTransfer.Conduction.BaseClasses.Examples.Temperature_u
Approximation of specific internal energy versus temperature curve with cubic hermite cubic spline
Information
This example tests and demonstrates the implementation of the specific internal energy versus temperature T(u) relationship for phase-change problems. Cubic hermite interpolation and linear extrapolation is used to approximate the piece-wise linear T(u) relationship. A piece-wise linear T(u) relationship is assumed in all three characteristic regions (solid, mushy and liquid). The example uses the functions Buildings.HeatTransfer.Conduction.BaseClasses.der_temperature_u and Buildings.HeatTransfer.Conduction.BaseClasses.temperature_u. The first function is used to compute the derivatives at the support points, and the second function computes the temperature for a given specific internal energy.
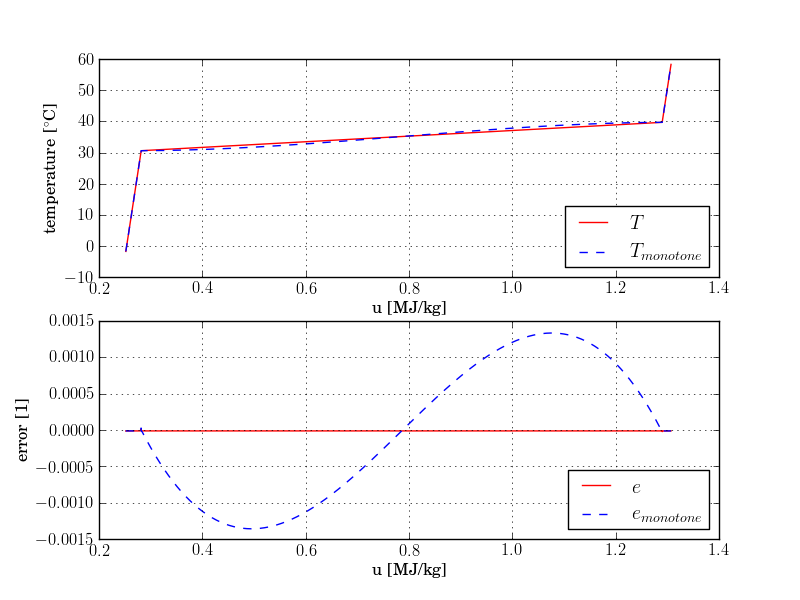
The example also demonstrates the use of cubic hermite spline interpolation with
two different settings: One produces an approximation of the T(u) relationship that is monotone,
whereas the other does not enforce monotonicity.
The latter one is used by default in the Buildings library,
since it produces a higher accuracy in the mushy
region, especially for materials in which phase-change transformation occurs in a wide
temperature interval (see the figure below).
The curves errNonMonotone and
errMonotone
represent the relative error between approximated and exact temperatures
obtained for different specific internal energy values (right hand side figure).
Extends from Modelica.Icons.Example (Icon for runnable examples).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Generic | materialMonotone | Phase change material with monotone u-T relation | |
| Generic | materialNonMonotone | Phase change material with non-monotone u-T relation | |
| SpecificInternalEnergy | ud[Buildings.HeatTransfer.Conduction.nSupPCM] | Support points [J/kg] | |
| SpecificInternalEnergy | udMonotone[Buildings.HeatTransfer.Conduction.nSupPCM] | Support points [J/kg] | |
| Temperature | Td[Buildings.HeatTransfer.Conduction.nSupPCM] | Support points [K] | |
| Temperature | TdMonotone[Buildings.HeatTransfer.Conduction.nSupPCM] | Support points [K] | |
| Real | dT_du[Buildings.HeatTransfer.Conduction.nSupPCM] | Derivatives at the support points - non-monotone, default in Modelica PCM [kg.K2/J] | |
| Real | dT_duMonotone[Buildings.HeatTransfer.Conduction.nSupPCM] | Derivatives at the support points for monotone increasing cubic splines [kg.K2/J] | |
| TemperatureDifference | dTCha | materialMonotone.TSol + mate... | Characteristic temperature difference of the problem [K] |