Buildings.Fluid.Actuators.Valves
Package with valve models
Information
This package contains component models for two- and three-way valves. For motor models, see Buildings.Fluid.Actuators.Motors.Extends from Modelica.Icons.VariantsPackage (Icon for package containing variants).
Package Content
| Name | Description |
|---|---|
| Three way valve with equal percentage and linear characteristics | |
| Three way valve with linear characteristics | |
| Two way valve with equal percentage flow characteristics | |
| Two way valve with linear flow characteristics | |
| Two way valve with polynomial characteristic | |
| Model of a pressure-independent two way valve | |
| Two way valve with quick opening flow characteristics | |
| Two way valve with table-specified flow characteristics | |
| Data records for table-based valves | |
| Collection of models that illustrate model use and test models | |
| Collection of validation models |
 Buildings.Fluid.Actuators.Valves.ThreeWayEqualPercentageLinear
Buildings.Fluid.Actuators.Valves.ThreeWayEqualPercentageLinear
Three way valve with equal percentage and linear characteristics
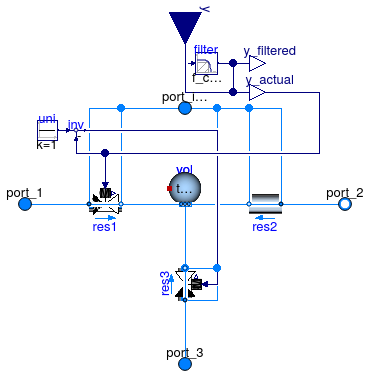
Information
Three way valve with equal percentage characteristics
between port_1 and port_2
and linear opening characteristic between port_3 and port_2.
Such opening characteristics were typical for valves from Landis & Gyr (now
Siemens).
This model is based on the partial valve models Buildings.Fluid.Actuators.BaseClasses.PartialThreeWayValve and Buildings.Fluid.Actuators.BaseClasses.PartialTwoWayValve. See Buildings.Fluid.Actuators.BaseClasses.PartialThreeWayValve for the implementation of the three way valve and see Buildings.Fluid.Actuators.BaseClasses.PartialTwoWayValve for the implementation of the regularization near the origin.
Extends from BaseClasses.PartialThreeWayValve (Partial three way valve).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| replaceable package Medium | PartialMedium | Medium in the component | |
| Real | fraK | 0.7 | Fraction Kv(port_3→port_2)/Kv(port_1→port_2) |
| Real | l[2] | {0.0001,0.0001} | Valve leakage, l=Kv(y=0)/Kv(y=1) |
| Real | R | 50 | Rangeability, R=50...100 typically |
| Real | delta0 | 0.01 | Range of significant deviation from equal percentage law |
| Flow Coefficient | |||
| CvTypes | CvData | Buildings.Fluid.Types.CvType... | Selection of flow coefficient |
| Real | Kv | Kv (metric) flow coefficient [m3/h/(bar)^(1/2)] | |
| Real | Cv | Cv (US) flow coefficient [USG/min/(psi)^(1/2)] | |
| Area | Av | Av (metric) flow coefficient [m2] | |
| Pressure-flow linearization | |||
| Real | deltaM | 0.02 | Fraction of nominal flow rate where linearization starts, if y=1 |
| Nominal condition | |||
| MassFlowRate | m_flow_nominal | Nominal mass flow rate [kg/s] | |
| PressureDifference | dpValve_nominal | Nominal pressure drop of fully open valve, used if CvData=Buildings.Fluid.Types.CvTypes.OpPoint [Pa] | |
| PressureDifference | dpFixed_nominal[2] | {0,0} | Nominal pressure drop of pipes and other equipment in flow legs at port_1 and port_3 [Pa] |
| Dynamics | |||
| Equations | |||
| Dynamics | energyDynamics | Modelica.Fluid.Types.Dynamic... | Type of energy balance: dynamic (3 initialization options) or steady state |
| Dynamics | massDynamics | energyDynamics | Type of mass balance: dynamic (3 initialization options) or steady state |
| Nominal condition | |||
| Time | tau | 10 | Time constant at nominal flow for dynamic energy and momentum balance [s] |
| Filtered opening | |||
| Boolean | use_inputFilter | true | = true, if opening is filtered with a 2nd order CriticalDamping filter |
| Time | riseTime | 120 | Rise time of the filter (time to reach 99.6 % of an opening step) [s] |
| Integer | order | 2 | Order of filter |
| Init | init | Modelica.Blocks.Types.Init.I... | Type of initialization (no init/steady state/initial state/initial output) |
| Real | y_start | 1 | Initial value of output |
| Initialization | |||
| AbsolutePressure | p_start | Medium.p_default | Start value of pressure [Pa] |
| Temperature | T_start | Medium.T_default | Start value of temperature [K] |
| MassFraction | X_start[Medium.nX] | Medium.X_default | Start value of mass fractions m_i/m [kg/kg] |
| ExtraProperty | C_start[Medium.nC] | fill(0, Medium.nC) | Start value of trace substances |
| ExtraProperty | C_nominal[Medium.nC] | fill(1E-2, Medium.nC) | Nominal value of trace substances. (Set to typical order of magnitude.) |
| Advanced | |||
| Boolean | from_dp | true | = true, use m_flow = f(dp) else dp = f(m_flow) |
| PortFlowDirection | portFlowDirection_1 | Modelica.Fluid.Types.PortFlo... | Flow direction for port_1 |
| PortFlowDirection | portFlowDirection_2 | Modelica.Fluid.Types.PortFlo... | Flow direction for port_2 |
| PortFlowDirection | portFlowDirection_3 | Modelica.Fluid.Types.PortFlo... | Flow direction for port_3 |
| Boolean | linearized[2] | {false,false} | = true, use linear relation between m_flow and dp for any flow rate |
| Boolean | homotopyInitialization | true | = true, use homotopy method |
| Nominal condition | |||
| Density | rhoStd | Medium.density_pTX(101325, 2... | Inlet density for which valve coefficients are defined [kg/m3] |
Connectors
| Type | Name | Description |
|---|---|---|
| FluidPort_a | port_1 | First port, typically inlet |
| FluidPort_b | port_2 | Second port, typically outlet |
| FluidPort_a | port_3 | Third port, can be either inlet or outlet |
| input RealInput | y | Actuator position (0: closed, 1: open) |
| output RealOutput | y_actual | Actual valve position |
Modelica definition
 Buildings.Fluid.Actuators.Valves.ThreeWayLinear
Buildings.Fluid.Actuators.Valves.ThreeWayLinear
Three way valve with linear characteristics
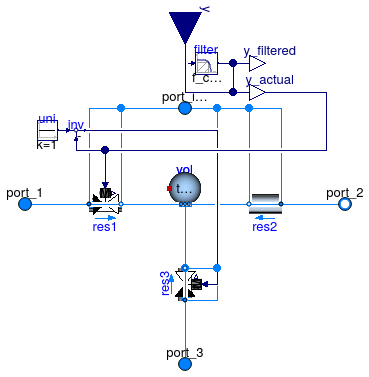
Information
Three way valve with linear opening characteristic.
This model is based on the partial valve models Buildings.Fluid.Actuators.BaseClasses.PartialThreeWayValve and Buildings.Fluid.Actuators.BaseClasses.PartialTwoWayValve. See Buildings.Fluid.Actuators.BaseClasses.PartialThreeWayValve for the implementation of the three way valve and see Buildings.Fluid.Actuators.BaseClasses.PartialTwoWayValve for the implementation of the regularization near the origin.
Extends from BaseClasses.PartialThreeWayValve (Partial three way valve).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| replaceable package Medium | PartialMedium | Medium in the component | |
| Real | fraK | 0.7 | Fraction Kv(port_3→port_2)/Kv(port_1→port_2) |
| Real | l[2] | {0.0001,0.0001} | Valve leakage, l=Kv(y=0)/Kv(y=1) |
| Flow Coefficient | |||
| CvTypes | CvData | Buildings.Fluid.Types.CvType... | Selection of flow coefficient |
| Real | Kv | Kv (metric) flow coefficient [m3/h/(bar)^(1/2)] | |
| Real | Cv | Cv (US) flow coefficient [USG/min/(psi)^(1/2)] | |
| Area | Av | Av (metric) flow coefficient [m2] | |
| Pressure-flow linearization | |||
| Real | deltaM | 0.02 | Fraction of nominal flow rate where linearization starts, if y=1 |
| Nominal condition | |||
| MassFlowRate | m_flow_nominal | Nominal mass flow rate [kg/s] | |
| PressureDifference | dpValve_nominal | Nominal pressure drop of fully open valve, used if CvData=Buildings.Fluid.Types.CvTypes.OpPoint [Pa] | |
| PressureDifference | dpFixed_nominal[2] | {0,0} | Nominal pressure drop of pipes and other equipment in flow legs at port_1 and port_3 [Pa] |
| Dynamics | |||
| Equations | |||
| Dynamics | energyDynamics | Modelica.Fluid.Types.Dynamic... | Type of energy balance: dynamic (3 initialization options) or steady state |
| Dynamics | massDynamics | energyDynamics | Type of mass balance: dynamic (3 initialization options) or steady state |
| Nominal condition | |||
| Time | tau | 10 | Time constant at nominal flow for dynamic energy and momentum balance [s] |
| Filtered opening | |||
| Boolean | use_inputFilter | true | = true, if opening is filtered with a 2nd order CriticalDamping filter |
| Time | riseTime | 120 | Rise time of the filter (time to reach 99.6 % of an opening step) [s] |
| Integer | order | 2 | Order of filter |
| Init | init | Modelica.Blocks.Types.Init.I... | Type of initialization (no init/steady state/initial state/initial output) |
| Real | y_start | 1 | Initial value of output |
| Initialization | |||
| AbsolutePressure | p_start | Medium.p_default | Start value of pressure [Pa] |
| Temperature | T_start | Medium.T_default | Start value of temperature [K] |
| MassFraction | X_start[Medium.nX] | Medium.X_default | Start value of mass fractions m_i/m [kg/kg] |
| ExtraProperty | C_start[Medium.nC] | fill(0, Medium.nC) | Start value of trace substances |
| ExtraProperty | C_nominal[Medium.nC] | fill(1E-2, Medium.nC) | Nominal value of trace substances. (Set to typical order of magnitude.) |
| Advanced | |||
| Boolean | from_dp | true | = true, use m_flow = f(dp) else dp = f(m_flow) |
| PortFlowDirection | portFlowDirection_1 | Modelica.Fluid.Types.PortFlo... | Flow direction for port_1 |
| PortFlowDirection | portFlowDirection_2 | Modelica.Fluid.Types.PortFlo... | Flow direction for port_2 |
| PortFlowDirection | portFlowDirection_3 | Modelica.Fluid.Types.PortFlo... | Flow direction for port_3 |
| Boolean | linearized[2] | {false,false} | = true, use linear relation between m_flow and dp for any flow rate |
| Boolean | homotopyInitialization | true | = true, use homotopy method |
| Nominal condition | |||
| Density | rhoStd | Medium.density_pTX(101325, 2... | Inlet density for which valve coefficients are defined [kg/m3] |
Connectors
| Type | Name | Description |
|---|---|---|
| FluidPort_a | port_1 | First port, typically inlet |
| FluidPort_b | port_2 | Second port, typically outlet |
| FluidPort_a | port_3 | Third port, can be either inlet or outlet |
| input RealInput | y | Actuator position (0: closed, 1: open) |
| output RealOutput | y_actual | Actual valve position |
Modelica definition
 Buildings.Fluid.Actuators.Valves.TwoWayEqualPercentage
Buildings.Fluid.Actuators.Valves.TwoWayEqualPercentage
Two way valve with equal percentage flow characteristics
Information
Two way valve with an equal percentage valve opening characteristic.
This model is based on the partial valve model Buildings.Fluid.Actuators.BaseClasses.PartialTwoWayValve. Check this model for more information, such as the regularization near the origin.
Extends from BaseClasses.PartialTwoWayValveKv (Partial model for a two way valve using a Kv characteristic).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| replaceable package Medium | PartialMedium | Medium in the component | |
| Real | l | 0.0001 | Valve leakage, l=Kv(y=0)/Kv(y=1) |
| Real | kFixed | if dpFixed_nominal > Modelic... | Flow coefficient of fixed resistance that may be in series with valve, k=m_flow/sqrt(dp), with unit=(kg.m)^(1/2). |
| Real | R | 50 | Rangeability, R=50...100 typically |
| Real | delta0 | 0.01 | Range of significant deviation from equal percentage law |
| Nominal condition | |||
| MassFlowRate | m_flow_nominal | Nominal mass flow rate [kg/s] | |
| PressureDifference | dpValve_nominal | Nominal pressure drop of fully open valve, used if CvData=Buildings.Fluid.Types.CvTypes.OpPoint [Pa] | |
| PressureDifference | dpFixed_nominal | 0 | Pressure drop of pipe and other resistances that are in series [Pa] |
| Flow Coefficient | |||
| CvTypes | CvData | Buildings.Fluid.Types.CvType... | Selection of flow coefficient |
| Real | Kv | Kv (metric) flow coefficient [m3/h/(bar)^(1/2)] | |
| Real | Cv | Cv (US) flow coefficient [USG/min/(psi)^(1/2)] | |
| Area | Av | Av (metric) flow coefficient [m2] | |
| Pressure-flow linearization | |||
| Real | deltaM | 0.02 | Fraction of nominal flow rate where linearization starts, if y=1 |
| Custom Parameters | |||
| Real | phi | if homotopyInitialization th... | Ratio actual to nominal mass flow rate of valve, phi=Kv(y)/Kv(y=1) |
| Assumptions | |||
| Boolean | allowFlowReversal | true | = false to simplify equations, assuming, but not enforcing, no flow reversal |
| Advanced | |||
| Diagnostics | |||
| Boolean | show_T | false | = true, if actual temperature at port is computed |
| Boolean | from_dp | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | homotopyInitialization | true | = true, use homotopy method |
| Boolean | linearized | false | = true, use linear relation between m_flow and dp for any flow rate |
| Nominal condition | |||
| Density | rhoStd | Medium.density_pTX(101325, 2... | Inlet density for which valve coefficients are defined [kg/m3] |
| Dynamics | |||
| Filtered opening | |||
| Boolean | use_inputFilter | true | = true, if opening is filtered with a 2nd order CriticalDamping filter |
| Time | riseTime | 120 | Rise time of the filter (time to reach 99.6 % of an opening step) [s] |
| Integer | order | 2 | Order of filter |
| Init | init | Modelica.Blocks.Types.Init.I... | Type of initialization (no init/steady state/initial state/initial output) |
| Real | y_start | 1 | Initial value of output |
Connectors
| Type | Name | Description |
|---|---|---|
| FluidPort_a | port_a | Fluid connector a (positive design flow direction is from port_a to port_b) |
| FluidPort_b | port_b | Fluid connector b (positive design flow direction is from port_a to port_b) |
| input RealInput | y | Actuator position (0: closed, 1: open) |
| output RealOutput | y_actual | Actual valve position |
Modelica definition
 Buildings.Fluid.Actuators.Valves.TwoWayLinear
Buildings.Fluid.Actuators.Valves.TwoWayLinear
Two way valve with linear flow characteristics

Information
Two way valve with linear opening characteristic.
This model is based on the partial valve model Buildings.Fluid.Actuators.BaseClasses.PartialTwoWayValve. Check this model for more information, such as the regularization near the origin.
Extends from BaseClasses.PartialTwoWayValveKv (Partial model for a two way valve using a Kv characteristic).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| replaceable package Medium | PartialMedium | Medium in the component | |
| Real | l | 0.0001 | Valve leakage, l=Kv(y=0)/Kv(y=1) |
| Real | kFixed | if dpFixed_nominal > Modelic... | Flow coefficient of fixed resistance that may be in series with valve, k=m_flow/sqrt(dp), with unit=(kg.m)^(1/2). |
| Nominal condition | |||
| MassFlowRate | m_flow_nominal | Nominal mass flow rate [kg/s] | |
| PressureDifference | dpValve_nominal | Nominal pressure drop of fully open valve, used if CvData=Buildings.Fluid.Types.CvTypes.OpPoint [Pa] | |
| PressureDifference | dpFixed_nominal | 0 | Pressure drop of pipe and other resistances that are in series [Pa] |
| Flow Coefficient | |||
| CvTypes | CvData | Buildings.Fluid.Types.CvType... | Selection of flow coefficient |
| Real | Kv | Kv (metric) flow coefficient [m3/h/(bar)^(1/2)] | |
| Real | Cv | Cv (US) flow coefficient [USG/min/(psi)^(1/2)] | |
| Area | Av | Av (metric) flow coefficient [m2] | |
| Pressure-flow linearization | |||
| Real | deltaM | 0.02 | Fraction of nominal flow rate where linearization starts, if y=1 |
| Custom Parameters | |||
| Real | phi | l + y_actual*(1 - l) | Ratio actual to nominal mass flow rate of valve, phi=Kv(y)/Kv(y=1) |
| Assumptions | |||
| Boolean | allowFlowReversal | true | = false to simplify equations, assuming, but not enforcing, no flow reversal |
| Advanced | |||
| Diagnostics | |||
| Boolean | show_T | false | = true, if actual temperature at port is computed |
| Boolean | from_dp | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | homotopyInitialization | true | = true, use homotopy method |
| Boolean | linearized | false | = true, use linear relation between m_flow and dp for any flow rate |
| Nominal condition | |||
| Density | rhoStd | Medium.density_pTX(101325, 2... | Inlet density for which valve coefficients are defined [kg/m3] |
| Dynamics | |||
| Filtered opening | |||
| Boolean | use_inputFilter | true | = true, if opening is filtered with a 2nd order CriticalDamping filter |
| Time | riseTime | 120 | Rise time of the filter (time to reach 99.6 % of an opening step) [s] |
| Integer | order | 2 | Order of filter |
| Init | init | Modelica.Blocks.Types.Init.I... | Type of initialization (no init/steady state/initial state/initial output) |
| Real | y_start | 1 | Initial value of output |
Connectors
| Type | Name | Description |
|---|---|---|
| FluidPort_a | port_a | Fluid connector a (positive design flow direction is from port_a to port_b) |
| FluidPort_b | port_b | Fluid connector b (positive design flow direction is from port_a to port_b) |
| input RealInput | y | Actuator position (0: closed, 1: open) |
| output RealOutput | y_actual | Actual valve position |
Modelica definition
 Buildings.Fluid.Actuators.Valves.TwoWayPolynomial
Buildings.Fluid.Actuators.Valves.TwoWayPolynomial
Two way valve with polynomial characteristic

Information
Two way valve with polynomial opening characteristic.
The polynomial coefficients are defined using parameter c.
The elements of c are coefficients for increasing powers of y,
starting with the power 0, which corresponds to a fixed offset.
This valve model can be used to implement valves with a custom
opening characteristic, such as a combination
of a linear and an equal percentage characteristic.
This model is based on the partial valve model Buildings.Fluid.Actuators.BaseClasses.PartialTwoWayValve. Check this model for more information, such as the regularization near the origin.
Extends from Buildings.Fluid.Actuators.BaseClasses.PartialTwoWayValveKv (Partial model for a two way valve using a Kv characteristic).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| replaceable package Medium | PartialMedium | Medium in the component | |
| Real | l | 0.0001 | Valve leakage, l=Kv(y=0)/Kv(y=1) |
| Real | kFixed | if dpFixed_nominal > Modelic... | Flow coefficient of fixed resistance that may be in series with valve, k=m_flow/sqrt(dp), with unit=(kg.m)^(1/2). |
| Real | c[:] | Polynomial coefficients, starting with fixed offset | |
| Nominal condition | |||
| MassFlowRate | m_flow_nominal | Nominal mass flow rate [kg/s] | |
| PressureDifference | dpValve_nominal | Nominal pressure drop of fully open valve, used if CvData=Buildings.Fluid.Types.CvTypes.OpPoint [Pa] | |
| PressureDifference | dpFixed_nominal | 0 | Pressure drop of pipe and other resistances that are in series [Pa] |
| Flow Coefficient | |||
| CvTypes | CvData | Buildings.Fluid.Types.CvType... | Selection of flow coefficient |
| Real | Kv | Kv (metric) flow coefficient [m3/h/(bar)^(1/2)] | |
| Real | Cv | Cv (US) flow coefficient [USG/min/(psi)^(1/2)] | |
| Area | Av | Av (metric) flow coefficient [m2] | |
| Pressure-flow linearization | |||
| Real | deltaM | 0.02 | Fraction of nominal flow rate where linearization starts, if y=1 |
| Custom Parameters | |||
| Real | phi | l + pol_y*(1 - l) | Ratio actual to nominal mass flow rate of valve, phi=Kv(y)/Kv(y=1) |
| Assumptions | |||
| Boolean | allowFlowReversal | true | = false to simplify equations, assuming, but not enforcing, no flow reversal |
| Advanced | |||
| Diagnostics | |||
| Boolean | show_T | false | = true, if actual temperature at port is computed |
| Boolean | from_dp | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | homotopyInitialization | true | = true, use homotopy method |
| Boolean | linearized | false | = true, use linear relation between m_flow and dp for any flow rate |
| Nominal condition | |||
| Density | rhoStd | Medium.density_pTX(101325, 2... | Inlet density for which valve coefficients are defined [kg/m3] |
| Dynamics | |||
| Filtered opening | |||
| Boolean | use_inputFilter | true | = true, if opening is filtered with a 2nd order CriticalDamping filter |
| Time | riseTime | 120 | Rise time of the filter (time to reach 99.6 % of an opening step) [s] |
| Integer | order | 2 | Order of filter |
| Init | init | Modelica.Blocks.Types.Init.I... | Type of initialization (no init/steady state/initial state/initial output) |
| Real | y_start | 1 | Initial value of output |
Connectors
| Type | Name | Description |
|---|---|---|
| FluidPort_a | port_a | Fluid connector a (positive design flow direction is from port_a to port_b) |
| FluidPort_b | port_b | Fluid connector b (positive design flow direction is from port_a to port_b) |
| input RealInput | y | Actuator position (0: closed, 1: open) |
| output RealOutput | y_actual | Actual valve position |
Modelica definition
 Buildings.Fluid.Actuators.Valves.TwoWayPressureIndependent
Buildings.Fluid.Actuators.Valves.TwoWayPressureIndependent
Model of a pressure-independent two way valve

Information
Two way valve with a pressure-independent valve opening characteristic.
The mass flow rate is controlled such that it is nearly equal to its
set point y*m_flow_nominal, unless the pressure
dp is too low, in which case a regular Kv
characteristic is used.
Main equations
First the minimum pressure head dp_min
required for delivering the requested mass flow rate
y*m_flow_nominal is computed. If
dp > dp_min then the requested mass flow
rate is supplied. If dp < dp_min then
m_flow = Kv/sqrt(dp). Transition between
these two flow regimes happens in a smooth way.
Typical use and important parameters
This model is configured by setting m_flow_nominal
to the mass flow rate that the valve should supply when it is
completely open, i.e., y = 1. The pressure drop corresponding
to this working point can be set using dpValve_nominal,
or using a Kv, Cv or Av
value. The parameter dpValve_fixed can be used to add
additional pressure drops, although in this valve it is equivalent to
add these to dpValve_nominal.
The parameter l2 represents the non-ideal
leakage behaviour of this valve for high pressures.
It is assumed that the mass flow rate will rise beyond
the requested mass flow rate y*m_flow_nominal
if dp > dpValve_nominal+dpFixed_nominal.
The parameter l2 represents the slope
of this rise:
d(m_flow)/d(dp) = l2* m_flow_nominal/dp_nominal.
In the ideal case l2=0, but
this may introduce singularities, for instance when
connecting this component with a fixed mass flow source.
Options
Parameter deltax sets the duration of
the transition region between the two flow regimes
as a fraction of dp_nominal or m_flow_nominal,
depending on the value of from_dp.
Implementation
Note that the result in the transition region when
using from_dp = true is not identical to
the result when using from_dp = false.
Variables *_y1 and *_y2
serve a dual use.
They are used to
1) compute the support points at *_x1 and *_x2,
which should not depend on m_flow or dp and
2) to compute the flow functions when outside of this regime,
which does depend on m_flow or dp.
Min and max functions are therefore used such that one equation
can serve both puroposes.
Extends from Buildings.Fluid.Actuators.BaseClasses.PartialTwoWayValve (Partial model for a two way valve).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| replaceable package Medium | PartialMedium | Medium in the component | |
| Real | l | 0.0001 | Valve leakage, l=Kv(y=0)/Kv(y=1) |
| Real | kFixed | if dpFixed_nominal > Modelic... | Flow coefficient of fixed resistance that may be in series with valve, k=m_flow/sqrt(dp), with unit=(kg.m)^(1/2). |
| Nominal condition | |||
| MassFlowRate | m_flow_nominal | Nominal mass flow rate [kg/s] | |
| PressureDifference | dpValve_nominal | Nominal pressure drop of fully open valve, used if CvData=Buildings.Fluid.Types.CvTypes.OpPoint [Pa] | |
| PressureDifference | dpFixed_nominal | 0 | Pressure drop of pipe and other resistances that are in series [Pa] |
| Flow Coefficient | |||
| CvTypes | CvData | Buildings.Fluid.Types.CvType... | Selection of flow coefficient |
| Real | Kv | Kv (metric) flow coefficient [m3/h/(bar)^(1/2)] | |
| Real | Cv | Cv (US) flow coefficient [USG/min/(psi)^(1/2)] | |
| Area | Av | Av (metric) flow coefficient [m2] | |
| Pressure-flow linearization | |||
| Real | deltaM | 0.02 | Fraction of nominal flow rate where linearization starts, if y=1 |
| Custom Parameters | |||
| Real | phi | l + y_actual*(1 - l) | Ratio actual to nominal mass flow rate of valve, phi=Kv(y)/Kv(y=1) |
| Assumptions | |||
| Boolean | allowFlowReversal | true | = false to simplify equations, assuming, but not enforcing, no flow reversal |
| Advanced | |||
| Diagnostics | |||
| Boolean | show_T | false | = true, if actual temperature at port is computed |
| Boolean | from_dp | true | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | homotopyInitialization | true | = true, use homotopy method |
| Boolean | linearized | false | = true, use linear relation between m_flow and dp for any flow rate |
| Real | l2 | 0.01 | Gain for mass flow increase if pressure is above nominal pressure |
| Real | deltax | 0.02 | Transition interval for flow rate |
| Nominal condition | |||
| Density | rhoStd | Medium.density_pTX(101325, 2... | Inlet density for which valve coefficients are defined [kg/m3] |
| Dynamics | |||
| Filtered opening | |||
| Boolean | use_inputFilter | true | = true, if opening is filtered with a 2nd order CriticalDamping filter |
| Time | riseTime | 120 | Rise time of the filter (time to reach 99.6 % of an opening step) [s] |
| Integer | order | 2 | Order of filter |
| Init | init | Modelica.Blocks.Types.Init.I... | Type of initialization (no init/steady state/initial state/initial output) |
| Real | y_start | 1 | Initial value of output |
Connectors
| Type | Name | Description |
|---|---|---|
| FluidPort_a | port_a | Fluid connector a (positive design flow direction is from port_a to port_b) |
| FluidPort_b | port_b | Fluid connector b (positive design flow direction is from port_a to port_b) |
| input RealInput | y | Actuator position (0: closed, 1: open) |
| output RealOutput | y_actual | Actual valve position |
Modelica definition
 Buildings.Fluid.Actuators.Valves.TwoWayQuickOpening
Buildings.Fluid.Actuators.Valves.TwoWayQuickOpening
Two way valve with quick opening flow characteristics

Information
Two way valve with a power function for the valve opening characteristic. Valves that need to open quickly typically have such a valve characteristics.
This model is based on the partial valve model Buildings.Fluid.Actuators.BaseClasses.PartialTwoWayValve. Check this model for more information, such as the regularization near the origin.
Extends from BaseClasses.PartialTwoWayValveKv (Partial model for a two way valve using a Kv characteristic).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| replaceable package Medium | PartialMedium | Medium in the component | |
| Real | l | 0.0001 | Valve leakage, l=Kv(y=0)/Kv(y=1) |
| Real | kFixed | if dpFixed_nominal > Modelic... | Flow coefficient of fixed resistance that may be in series with valve, k=m_flow/sqrt(dp), with unit=(kg.m)^(1/2). |
| Real | alp | 2 | Parameter for valve characteristics, alp>0 |
| Real | delta0 | 0.01 | Range of significant deviation from power law |
| Nominal condition | |||
| MassFlowRate | m_flow_nominal | Nominal mass flow rate [kg/s] | |
| PressureDifference | dpValve_nominal | Nominal pressure drop of fully open valve, used if CvData=Buildings.Fluid.Types.CvTypes.OpPoint [Pa] | |
| PressureDifference | dpFixed_nominal | 0 | Pressure drop of pipe and other resistances that are in series [Pa] |
| Flow Coefficient | |||
| CvTypes | CvData | Buildings.Fluid.Types.CvType... | Selection of flow coefficient |
| Real | Kv | Kv (metric) flow coefficient [m3/h/(bar)^(1/2)] | |
| Real | Cv | Cv (US) flow coefficient [USG/min/(psi)^(1/2)] | |
| Area | Av | Av (metric) flow coefficient [m2] | |
| Pressure-flow linearization | |||
| Real | deltaM | 0.02 | Fraction of nominal flow rate where linearization starts, if y=1 |
| Custom Parameters | |||
| Real | phi | if homotopyInitialization th... | Ratio actual to nominal mass flow rate of valve, phi=Kv(y)/Kv(y=1) |
| Assumptions | |||
| Boolean | allowFlowReversal | true | = false to simplify equations, assuming, but not enforcing, no flow reversal |
| Advanced | |||
| Diagnostics | |||
| Boolean | show_T | false | = true, if actual temperature at port is computed |
| Boolean | from_dp | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | homotopyInitialization | true | = true, use homotopy method |
| Boolean | linearized | false | = true, use linear relation between m_flow and dp for any flow rate |
| Nominal condition | |||
| Density | rhoStd | Medium.density_pTX(101325, 2... | Inlet density for which valve coefficients are defined [kg/m3] |
| Dynamics | |||
| Filtered opening | |||
| Boolean | use_inputFilter | true | = true, if opening is filtered with a 2nd order CriticalDamping filter |
| Time | riseTime | 120 | Rise time of the filter (time to reach 99.6 % of an opening step) [s] |
| Integer | order | 2 | Order of filter |
| Init | init | Modelica.Blocks.Types.Init.I... | Type of initialization (no init/steady state/initial state/initial output) |
| Real | y_start | 1 | Initial value of output |
Connectors
| Type | Name | Description |
|---|---|---|
| FluidPort_a | port_a | Fluid connector a (positive design flow direction is from port_a to port_b) |
| FluidPort_b | port_b | Fluid connector b (positive design flow direction is from port_a to port_b) |
| input RealInput | y | Actuator position (0: closed, 1: open) |
| output RealOutput | y_actual | Actual valve position |
Modelica definition
 Buildings.Fluid.Actuators.Valves.TwoWayTable
Buildings.Fluid.Actuators.Valves.TwoWayTable
Two way valve with table-specified flow characteristics
Information
Two way valve with opening characteristic that is configured through a table.
The mass flow rate for the fully open valve is determined based
on the value of the parameter CvData.
For the different valve positions y ∈ [0, 1], this nominal flow rate is
scaled by the values of the parameter
flowCharacteristics.
The parameter flowCharacteristics declares a table of the form
| y | 0 | ... | 1 |
| φ | l | ... | 1 |
where l = Kv(y=0)/Kv(y=1) > 0 is the valve leakage. The first row is the valve opening, and the second row is the mass flow rate, relative to the mass flow rate of the fully open valve, under the assumption of a constant pressure difference across the valve. A suggested value for the valve leakage is l=0.0001. If l = 0, then this model will replace it with l = 10-8 for numerical reasons. For example, if a valve has Kv=0.5 [m3/h/bar1/2] and a linear opening characteristics and a valve leakage of l=0.0001, then one would set
CvData=Buildings.Fluid.Types.CvTypes.Kv
Kv = 0.5
flowCharacteristics(y={0,1}, phi={0.0001,1})
Note, however, that Buildings.Fluid.Actuators.Valves.TwoWayLinear provides a more efficient implementation for this simple case.
The parameter flowCharacteristics must meet the following
requirements, otherwise the model stops with an error:
-
The arrays in
flowCharacteristics.yandflowCharacteristics.phimust be strictly monotonic increasing. -
The first value must satisfy
flowCharacteristics.y[1]=0, andflowCharacteristics.phi[1]must be equal to the leakage flow rate, which must be bigger than zero. Otherwise, a default value of1E-8is used. -
The last values must satisfy
flowCharacteristics.y[end]=1andflowCharacteristics.phi[end]=1.
This model is based on the partial valve model Buildings.Fluid.Actuators.BaseClasses.PartialTwoWayValve. Check this model for more information, such as the regularization near the origin.
For an example that specifies an opening characteristics, see Buildings.Fluid.Actuators.Valves.Examples.TwoWayValveTable.
Extends from BaseClasses.PartialTwoWayValveKv (Partial model for a two way valve using a Kv characteristic).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| replaceable package Medium | PartialMedium | Medium in the component | |
| Real | l | phiLooUp.table[1, 2] | Valve leakage, l=Kv(y=0)/Kv(y=1) |
| Real | kFixed | if dpFixed_nominal > Modelic... | Flow coefficient of fixed resistance that may be in series with valve, k=m_flow/sqrt(dp), with unit=(kg.m)^(1/2). |
| Generic | flowCharacteristics | Table with flow characteristics | |
| Nominal condition | |||
| MassFlowRate | m_flow_nominal | Nominal mass flow rate [kg/s] | |
| PressureDifference | dpValve_nominal | Nominal pressure drop of fully open valve, used if CvData=Buildings.Fluid.Types.CvTypes.OpPoint [Pa] | |
| PressureDifference | dpFixed_nominal | 0 | Pressure drop of pipe and other resistances that are in series [Pa] |
| Flow Coefficient | |||
| CvTypes | CvData | Buildings.Fluid.Types.CvType... | Selection of flow coefficient |
| Real | Kv | Kv (metric) flow coefficient [m3/h/(bar)^(1/2)] | |
| Real | Cv | Cv (US) flow coefficient [USG/min/(psi)^(1/2)] | |
| Area | Av | Av (metric) flow coefficient [m2] | |
| Pressure-flow linearization | |||
| Real | deltaM | 0.02 | Fraction of nominal flow rate where linearization starts, if y=1 |
| Custom Parameters | |||
| Real | phi | phiLooUp.y[1] | Ratio actual to nominal mass flow rate of valve, phi=Kv(y)/Kv(y=1) |
| Assumptions | |||
| Boolean | allowFlowReversal | true | = false to simplify equations, assuming, but not enforcing, no flow reversal |
| Advanced | |||
| Diagnostics | |||
| Boolean | show_T | false | = true, if actual temperature at port is computed |
| Boolean | from_dp | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | homotopyInitialization | true | = true, use homotopy method |
| Boolean | linearized | false | = true, use linear relation between m_flow and dp for any flow rate |
| Nominal condition | |||
| Density | rhoStd | Medium.density_pTX(101325, 2... | Inlet density for which valve coefficients are defined [kg/m3] |
| Dynamics | |||
| Filtered opening | |||
| Boolean | use_inputFilter | true | = true, if opening is filtered with a 2nd order CriticalDamping filter |
| Time | riseTime | 120 | Rise time of the filter (time to reach 99.6 % of an opening step) [s] |
| Integer | order | 2 | Order of filter |
| Init | init | Modelica.Blocks.Types.Init.I... | Type of initialization (no init/steady state/initial state/initial output) |
| Real | y_start | 1 | Initial value of output |
Connectors
| Type | Name | Description |
|---|---|---|
| FluidPort_a | port_a | Fluid connector a (positive design flow direction is from port_a to port_b) |
| FluidPort_b | port_b | Fluid connector b (positive design flow direction is from port_a to port_b) |
| input RealInput | y | Actuator position (0: closed, 1: open) |
| output RealOutput | y_actual | Actual valve position |
