LBL logo

Buildings.Fluid.HeatExchangers.CoolingTowers

Package with cooling tower models

Information

This package contains components models for cooling towers.

The model Buildings.Fluid.HeatExchangers.CoolingTowers.FixedApproach computes a fixed approach temperature.

The model Buildings.Fluid.HeatExchangers.CoolingTowers.YorkCalc computes the cooling tower performance based the York formula.

Extends from Modelica.Icons.VariantsPackage (Icon for package containing variants).

Package Content

Name Description
Buildings.Fluid.HeatExchangers.CoolingTowers.FixedApproach FixedApproach Cooling tower with constant approach temperature
Buildings.Fluid.HeatExchangers.CoolingTowers.YorkCalc YorkCalc Cooling tower with variable speed using the York calculation for the approach temperature
Buildings.Fluid.HeatExchangers.CoolingTowers.Correlations Correlations Package with correlations for cooling tower performance
Buildings.Fluid.HeatExchangers.CoolingTowers.Examples Examples Collection of models that illustrate model use and test models
Buildings.Fluid.HeatExchangers.CoolingTowers.BaseClasses BaseClasses Package with base classes for Buildings.Fluid.HeatExchangers.CoolingTowers

Buildings.Fluid.HeatExchangers.CoolingTowers.FixedApproach Buildings.Fluid.HeatExchangers.CoolingTowers.FixedApproach

Cooling tower with constant approach temperature

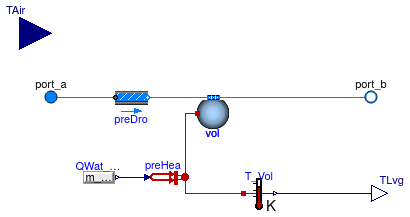
Buildings.Fluid.HeatExchangers.CoolingTowers.FixedApproach

Information

Model for a steady-state or dynamic cooling tower with constant approach temperature. The approach temperature is the difference between the leaving water temperature and the entering air temperature. The entering air temperature is used from the signal TAir. If connected to the a dry-bulb temperature, then a dry cooling tower is modeled. If connected to a wet-bulb temperature, then a wet cooling tower is modeled.

By connecting a signal that contains either the dry-bulb or the wet-bulb temperature, this model can be used to estimate the water return temperature from a cooling tower. For a more detailed model, use for example the YorkCalc model.

Extends from Buildings.Fluid.HeatExchangers.CoolingTowers.BaseClasses.CoolingTower (Base class for cooling towers).

Parameters

TypeNameDefaultDescription
replaceable package MediumPartialMediumMedium in the component
TemperatureDifferenceTApp2Approach temperature difference [K]
Nominal condition
MassFlowRatem_flow_nominal Nominal mass flow rate [kg/s]
PressureDifferencedp_nominal Pressure difference [Pa]
Initialization
MassFlowRatem_flow.start0Mass flow rate from port_a to port_b (m_flow > 0 is design flow direction) [kg/s]
PressureDifferencedp.start0Pressure difference between port_a and port_b [Pa]
Assumptions
BooleanallowFlowReversaltrue= true to allow flow reversal, false restricts to design direction (port_a -> port_b)
Advanced
MassFlowRatem_flow_small1E-4*abs(m_flow_nominal)Small mass flow rate for regularization of zero flow [kg/s]
BooleanhomotopyInitializationtrue= true, use homotopy method
Diagnostics
Booleanshow_Tfalse= true, if actual temperature at port is computed
Flow resistance
Booleanfrom_dpfalse= true, use m_flow = f(dp) else dp = f(m_flow)
BooleanlinearizeFlowResistancefalse= true, use linear relation between m_flow and dp for any flow rate
RealdeltaM0.1Fraction of nominal flow rate where flow transitions to laminar
Dynamics
Nominal condition
Timetau30Time constant at nominal flow (if energyDynamics <> SteadyState) [s]
Equations
DynamicsenergyDynamicsModelica.Fluid.Types.Dynamic...Type of energy balance: dynamic (3 initialization options) or steady state
DynamicsmassDynamicsenergyDynamicsType of mass balance: dynamic (3 initialization options) or steady state
Initialization
AbsolutePressurep_startMedium.p_defaultStart value of pressure [Pa]
TemperatureT_startMedium.T_defaultStart value of temperature [K]
MassFractionX_start[Medium.nX]Medium.X_defaultStart value of mass fractions m_i/m [kg/kg]
ExtraPropertyC_start[Medium.nC]fill(0, Medium.nC)Start value of trace substances

Connectors

TypeNameDescription
FluidPort_aport_aFluid connector a (positive design flow direction is from port_a to port_b)
FluidPort_bport_bFluid connector b (positive design flow direction is from port_a to port_b)
output RealOutputTLvgLeaving water temperature
input RealInputTAirEntering air dry or wet bulb temperature [K]

Modelica definition

model FixedApproach "Cooling tower with constant approach temperature" extends Buildings.Fluid.HeatExchangers.CoolingTowers.BaseClasses.CoolingTower; parameter Modelica.SIunits.TemperatureDifference TApp(min=0, displayUnit="K") = 2 "Approach temperature difference"; Modelica.Blocks.Interfaces.RealInput TAir(min=0, unit="K") "Entering air dry or wet bulb temperature"; equation TAppAct=TApp; TAirHT=TAir; end FixedApproach;

Buildings.Fluid.HeatExchangers.CoolingTowers.YorkCalc Buildings.Fluid.HeatExchangers.CoolingTowers.YorkCalc

Cooling tower with variable speed using the York calculation for the approach temperature

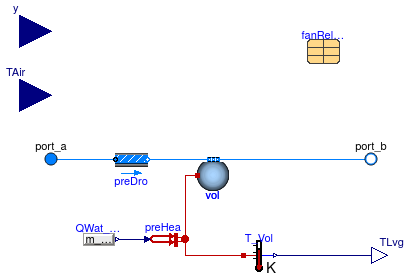
Buildings.Fluid.HeatExchangers.CoolingTowers.YorkCalc

Information

Model for a steady-state or dynamic cooling tower with variable speed fan using the York calculation for the approach temperature at off-design conditions.

Thermal performance

To compute the thermal performance, this model takes as parameters the approach temperature, the range temperature and the inlet air wet bulb temperature at the design condition. Since the design mass flow rate (of the chiller condenser loop) is also a parameter, these parameters define the rejected heat.

For off-design conditions, the model uses the actual range temperature and a polynomial to compute the approach temperature for free convection and for forced convection, i.e., with the fan operating. The polynomial is valid for a York cooling tower. If the fan input signal y is below the minimum fan revolution yMin, then the cooling tower operates in free convection mode, otherwise it operates in the forced convection mode. For numerical reasons, this transition occurs in the range of y ∈ [0.9*yMin, yMin].

Fan power consumption

The fan power consumption at the design condition can be specified as follows:

In the forced convection mode, the actual fan power is computed as PFan=fanRelPow(y) * PFan_nominal, where the default value for the fan relative power consumption at part load is fanRelPow(y)=y3. In the free convection mode, the fan power consumption is zero. For numerical reasons, the transition of fan power from the part load mode to zero power consumption in the free convection mode occurs in the range y ∈ [0.9*yMin, yMin].
To change the fan relative power consumption at part load in the forced convection mode, points of fan controls signal and associated relative power consumption can be specified. In between these points, the values are interpolated using cubic splines.

Comparison the cooling tower model of EnergyPlus

This model is similar to the model Cooling Tower:Variable Speed that is implemented in the EnergyPlus building energy simulation program version 6.0. The main differences are

  1. Not implemented are the basin heater power consumption, and the make-up water usage.
  2. The model has no built-in control to switch individual cells of the tower on or off. To switch cells on or off, use multiple instances of this model, and use your own control law to compute the input signal y.

Assumptions and limitations

This model requires a medium that has the same computation of the enthalpy as Buildings.Media.Water, which computes

h = cp (T-T0),

where h is the enthalpy, cp = 4184 J/(kg K) is the specific heat capacity, T is the temperature in Kelvin and T0 = 273.15 Kelvin. If this is not the case, the simulation will stop with an error message. The reason for this limitation is that as of January 2015, OpenModelica failed to translate the model if Medium.temperature() is used instead of Water.temperature().

References

EnergyPlus 2.0.0 Engineering Reference, April 9, 2007.

Extends from Buildings.Fluid.HeatExchangers.CoolingTowers.BaseClasses.CoolingTower (Base class for cooling towers).

Parameters

TypeNameDefaultDescription
replaceable package MediumPartialMediumMedium in the component
RealfraPFan_nominal275/0.15Fan power divived by water mass flow rate at design condition [W/(kg/s)]
PowerPFan_nominalfraPFan_nominal*m_flow_nominalFan power [W]
efficiencyParametersfanRelPow Fan relative power consumption as a function of control signal, fanRelPow=P(y)/P(y=1)
RealyMin0.3Minimum control signal until fan is switched off (used for smoothing between forced and free convection regime)
RealfraFreCon0.125Fraction of tower capacity in free convection regime
Nominal condition
MassFlowRatem_flow_nominal Nominal mass flow rate [kg/s]
PressureDifferencedp_nominal Pressure difference [Pa]
TemperatureTAirInWB_nominal273.15 + 25.55Design inlet air wet bulb temperature [K]
TemperatureDifferenceTApp_nominal3.89Design approach temperature [K]
TemperatureDifferenceTRan_nominal5.56Design range temperature (water in - water out) [K]
Initialization
MassFlowRatem_flow.start0Mass flow rate from port_a to port_b (m_flow > 0 is design flow direction) [kg/s]
PressureDifferencedp.start0Pressure difference between port_a and port_b [Pa]
Assumptions
BooleanallowFlowReversaltrue= true to allow flow reversal, false restricts to design direction (port_a -> port_b)
Advanced
MassFlowRatem_flow_small1E-4*abs(m_flow_nominal)Small mass flow rate for regularization of zero flow [kg/s]
BooleanhomotopyInitializationtrue= true, use homotopy method
Diagnostics
Booleanshow_Tfalse= true, if actual temperature at port is computed
Flow resistance
Booleanfrom_dpfalse= true, use m_flow = f(dp) else dp = f(m_flow)
BooleanlinearizeFlowResistancefalse= true, use linear relation between m_flow and dp for any flow rate
RealdeltaM0.1Fraction of nominal flow rate where flow transitions to laminar
Dynamics
Nominal condition
Timetau30Time constant at nominal flow (if energyDynamics <> SteadyState) [s]
Equations
DynamicsenergyDynamicsModelica.Fluid.Types.Dynamic...Type of energy balance: dynamic (3 initialization options) or steady state
DynamicsmassDynamicsenergyDynamicsType of mass balance: dynamic (3 initialization options) or steady state
Initialization
AbsolutePressurep_startMedium.p_defaultStart value of pressure [Pa]
TemperatureT_startMedium.T_defaultStart value of temperature [K]
MassFractionX_start[Medium.nX]Medium.X_defaultStart value of mass fractions m_i/m [kg/kg]
ExtraPropertyC_start[Medium.nC]fill(0, Medium.nC)Start value of trace substances

Connectors

TypeNameDescription
FluidPort_aport_aFluid connector a (positive design flow direction is from port_a to port_b)
FluidPort_bport_bFluid connector b (positive design flow direction is from port_a to port_b)
output RealOutputTLvgLeaving water temperature
input RealInputTAirEntering air wet bulb temperature [K]
input RealInputyFan control signal

Modelica definition

model YorkCalc "Cooling tower with variable speed using the York calculation for the approach temperature" extends Buildings.Fluid.HeatExchangers.CoolingTowers.BaseClasses.CoolingTower; import cha = Buildings.Fluid.HeatExchangers.CoolingTowers.BaseClasses.Characteristics; parameter Modelica.SIunits.Temperature TAirInWB_nominal = 273.15+25.55 "Design inlet air wet bulb temperature"; parameter Modelica.SIunits.TemperatureDifference TApp_nominal(displayUnit="K") = 3.89 "Design approach temperature"; parameter Modelica.SIunits.TemperatureDifference TRan_nominal(displayUnit="K") = 5.56 "Design range temperature (water in - water out)"; parameter Real fraPFan_nominal(unit="W/(kg/s)") = 275/0.15 "Fan power divived by water mass flow rate at design condition"; parameter Modelica.SIunits.Power PFan_nominal = fraPFan_nominal*m_flow_nominal "Fan power"; parameter cha.efficiencyParameters fanRelPow( r_V = {0, 0.1, 0.3, 0.6, 1}, eta = {0, 0.1^3, 0.3^3, 0.6^3, 1}) "Fan relative power consumption as a function of control signal, fanRelPow=P(y)/P(y=1)"; parameter Real yMin(min=0.01, max=1) = 0.3 "Minimum control signal until fan is switched off (used for smoothing between forced and free convection regime)"; parameter Real fraFreCon(min=0, max=1) = 0.125 "Fraction of tower capacity in free convection regime"; Modelica.Blocks.Interfaces.RealInput TAir(min=0, unit="K") "Entering air wet bulb temperature"; Buildings.Fluid.HeatExchangers.CoolingTowers.Correlations.BoundsYorkCalc bou "Bounds for correlation"; Modelica.Blocks.Interfaces.RealInput y "Fan control signal"; Modelica.SIunits.TemperatureDifference TRan(nominal=1, displayUnit="K") "Range temperature"; Modelica.SIunits.MassFraction FRWat "Ratio actual over design water mass flow ratio"; Modelica.SIunits.MassFraction FRAir "Ratio actual over design air mass flow ratio"; Modelica.SIunits.Power PFan "Fan power"; protected package Water = Buildings.Media.Water "Medium package for water"; parameter Modelica.SIunits.MassFraction FRWat0(min=0, start=1, fixed=false) "Ratio actual over design water mass flow ratio at nominal condition"; parameter Modelica.SIunits.Temperature TWatIn0(fixed=false) "Water inlet temperature at nominal condition"; parameter Modelica.SIunits.Temperature TWatOut_nominal(fixed=false) "Water outlet temperature at nominal condition"; parameter Modelica.SIunits.MassFlowRate mRef_flow(min=0, start=m_flow_nominal, fixed=false) "Reference water flow rate"; Modelica.SIunits.TemperatureDifference dTMax(nominal=1, displayUnit="K") "Maximum possible temperature difference"; Modelica.SIunits.TemperatureDifference TAppCor(min=0, nominal=1, displayUnit="K") "Approach temperature for forced convection"; Modelica.SIunits.TemperatureDifference TAppFreCon(min=0, nominal=1, displayUnit="K") "Approach temperature for free convection"; final parameter Real fanRelPowDer[size(fanRelPow.r_V,1)](each fixed=false) "Coefficients for fan relative power consumption as a function of control signal"; Modelica.SIunits.Temperature T_a "Temperature in port_a"; Modelica.SIunits.Temperature T_b "Temperature in port_b"; initial equation TWatOut_nominal = TAirInWB_nominal + TApp_nominal; TRan_nominal = TWatIn0 - TWatOut_nominal; // by definition of the range temp. TApp_nominal = Buildings.Fluid.HeatExchangers.CoolingTowers.Correlations.yorkCalc( TRan=TRan_nominal, TWetBul=TAirInWB_nominal, FRWat=FRWat0, FRAir=1); // this will be solved for FRWat0 mRef_flow = m_flow_nominal/FRWat0; // Derivatives for spline that interpolates the fan relative power fanRelPowDer = Buildings.Utilities.Math.Functions.splineDerivatives( x=fanRelPow.r_V, y=fanRelPow.eta, ensureMonotonicity=Buildings.Utilities.Math.Functions.isMonotonic(x=fanRelPow.eta, strict=false)); // Check validity of relative fan power consumption at y=yMin and y=1 assert(cha.efficiency(per=fanRelPow, r_V=yMin, d=fanRelPowDer) > -1E-4, "The fan relative power consumption must be non-negative for y=0." + "\n Obtained fanRelPow(0) = " + String(cha.efficiency(per=fanRelPow, r_V=yMin, d=fanRelPowDer)) + "\n You need to choose different values for the parameter fanRelPow."); assert(abs(1-cha.efficiency(per=fanRelPow, r_V=1, d=fanRelPowDer))<1E-4, "The fan relative power consumption must be one for y=1." + "\n Obtained fanRelPow(1) = " + String(cha.efficiency(per=fanRelPow, r_V=1, d=fanRelPowDer)) + "\n You need to choose different values for the parameter fanRelPow." + "\n To increase the fan power, change fraPFan_nominal or PFan_nominal."); // Check that a medium is used that has the same definition of enthalpy vs. temperature. // This is needed because below, T_a=Water.temperature needed to be hard-coded to use // Water.* instead of Medium.* in the function calls due to a bug in OpenModelica. assert(abs(Medium.specificEnthalpy_pTX(p=101325, T=273.15, X=Medium.X_default) - Water.specificEnthalpy_pTX(p=101325, T=273.15, X=Medium.X_default)) < 1E-5 and abs(Medium.specificEnthalpy_pTX(p=101325, T=293.15, X=Medium.X_default) - Water.specificEnthalpy_pTX(p=101325, T=293.15, X=Medium.X_default)) < 1E-5, "The selected medium has an enthalpy computation that is not consistent with the one in Buildings.Media.Water Use a different medium, such as Buildings.Media.Water."); equation // States at the inlet and outlet if allowFlowReversal then if homotopyInitialization then T_a=Water.temperature(Water.setState_phX(p=port_a.p, h=homotopy(actual=actualStream(port_a.h_outflow), simplified=inStream(port_a.h_outflow)), X=homotopy(actual=actualStream(port_a.Xi_outflow), simplified=inStream(port_a.Xi_outflow)))); T_b=Water.temperature(Water.setState_phX(p=port_b.p, h=homotopy(actual=actualStream(port_b.h_outflow), simplified=port_b.h_outflow), X=homotopy(actual=actualStream(port_b.Xi_outflow), simplified=port_b.Xi_outflow))); else T_a=Water.temperature(Water.setState_phX(p=port_a.p, h=actualStream(port_a.h_outflow), X=actualStream(port_a.Xi_outflow))); T_b=Water.temperature(Water.setState_phX(p=port_b.p, h=actualStream(port_b.h_outflow), X=actualStream(port_b.Xi_outflow))); end if; // homotopyInitialization else // reverse flow not allowed T_a=Water.temperature(Water.setState_phX(p=port_a.p, h=inStream(port_a.h_outflow), X=inStream(port_a.Xi_outflow))); T_b=Water.temperature(Water.setState_phX(p=port_b.p, h=inStream(port_b.h_outflow), X=inStream(port_b.Xi_outflow))); end if; // Air temperature used for the heat transfer TAirHT=TAir; // Range temperature TRan = T_a - T_b; // Fractional mass flow rates FRWat = m_flow/mRef_flow; FRAir = y; TAppCor = Buildings.Fluid.HeatExchangers.CoolingTowers.Correlations.yorkCalc( TRan=TRan, TWetBul=TAir, FRWat=FRWat, FRAir=Buildings.Utilities.Math.Functions.smoothMax( x1=FRWat/bou.liqGasRat_max, x2=FRAir, deltaX=0.01)); dTMax = T_a - TAir; TAppFreCon = (1-fraFreCon) * dTMax + fraFreCon * Buildings.Fluid.HeatExchangers.CoolingTowers.Correlations.yorkCalc( TRan=TRan, TWetBul=TAir, FRWat=FRWat, FRAir=1); // Actual approach temperature and fan power consumption, // which depends on forced vs. free convection. // The transition is for y in [yMin-yMin/10, yMin] [TAppAct, PFan] = Buildings.Utilities.Math.Functions.spliceFunction( pos=[TAppCor, cha.efficiency( per=fanRelPow, r_V=y, d=fanRelPowDer) * PFan_nominal], neg=[TAppFreCon, 0], x=y-yMin+yMin/20, deltax=yMin/20); end YorkCalc;
http://simulationresearch.lbl.gov/modelica