Buildings.Utilities.Math

Home > Modelica

Buildings.Utilities.Math

Library with functions such as for smoothing

Information

This package contains blocks and functions for commonly used mathematical operations. The classes in this package augment the classes Modelica.Blocks.

Extends from Modelica.Icons.Package (Icon for standard packages).

Package Content

Name	Description
$Buildings.Utilities.Math.Average$ Average	Average of a vector
$Buildings.Utilities.Math.Bicubic$ Bicubic	Bicubic function
$Buildings.Utilities.Math.Biquadratic$ Biquadratic	Biquadratic function
$Buildings.Utilities.Math.BooleanReplicator$ BooleanReplicator	Boolean signal replicator
$Buildings.Utilities.Math.IntegerReplicator$ IntegerReplicator	Integer signal replicator
$Buildings.Utilities.Math.InverseXRegularized$ InverseXRegularized	Function that approximates 1/x by a twice continuously differentiable function
$Buildings.Utilities.Math.Max$ Max	Maximum element of a vector
$Buildings.Utilities.Math.Min$ Min	Minimum element of a vector
$Buildings.Utilities.Math.Polynominal$ Polynominal	Polynominal function
$Buildings.Utilities.Math.PowerLinearized$ PowerLinearized	Power function that is linearized below a user-defined threshold
$Buildings.Utilities.Math.QuadraticLinear$ QuadraticLinear	Function that is quadratic in first argument and linear in second argument
$Buildings.Utilities.Math.RegNonZeroPower$ RegNonZeroPower	Power function, regularized near zero, but nonzero value for x=0
$Buildings.Utilities.Math.SmoothExponential$ SmoothExponential	Once continuously differentiable approximation to exp(-\|x\|) in interval \|x\| < delta
$Buildings.Utilities.Math.SmoothHeaviside$ SmoothHeaviside	Once continuously differentiable approximation to the Heaviside function
$Buildings.Utilities.Math.SmoothLimit$ SmoothLimit	Once continuously differentiable approximation to the limit function
$Buildings.Utilities.Math.SmoothMax$ SmoothMax	Once continuously differentiable approximation to the maximum function
$Buildings.Utilities.Math.SmoothMin$ SmoothMin	Once continuously differentiable approximation to the minimum function
$Buildings.Utilities.Math.Splice$ Splice	Block for splice function opertation
$Buildings.Utilities.Math.TrapezoidalIntegration$ TrapezoidalIntegration	Integration using the trapezoidal rule
$Buildings.Utilities.Math.Functions$ Functions	Package with mathematical functions
$Buildings.Utilities.Math.Examples$ Examples	Collection of models that illustrate model use and test models

$Buildings.Utilities.Math.Average$ Buildings.Utilities.Math.Average

Average of a vector

$Buildings.Utilities.Math.Average$

Information

This block outputs the average of the vector.

Extends from Modelica.Blocks.Interfaces.MISO (Multiple Input Single Output continuous control block).

Parameters

Type	Name	Default	Description
Integer	nin	1	Number of inputs

Connectors

Type	Name	Description
input RealInput	u[nin]	Connector of Real input signals
output RealOutput	y	Connector of Real output signal

Modelica definition

block Average "Average of a vector" extends Modelica.Blocks.Interfaces.MISO; equation y = Buildings.Utilities.Math.Functions.average(u=u, nin=nin); end Average;

$Buildings.Utilities.Math.Bicubic$ Buildings.Utilities.Math.Bicubic

Bicubic function

$Buildings.Utilities.Math.Bicubic$

Information

This block computes

y = a₁ + a₂ x₁ + a₃ x₁² + a₄ x₂ + a₅ x₂² + a₆ x₁ x₂ + a₇ x₁^3 + a₈ x₂^3 + a₉ x₁² x₂ + a₁0 x₁ x₂²

Extends from Modelica.Blocks.Interfaces.SI2SO (2 Single Input / 1 Single Output continuous control block).

Connectors

Type	Name	Description
input RealInput	u1	Connector of Real input signal 1
input RealInput	u2	Connector of Real input signal 2
output RealOutput	y	Connector of Real output signal

Modelica definition

block Bicubic "Bicubic function" extends Modelica.Blocks.Interfaces.SI2SO; input Real a[10] "Coefficients"; equation y = Buildings.Utilities.Math.Functions.bicubic(a=a, x1=u1, x2=u2); end Bicubic;

$Buildings.Utilities.Math.Biquadratic$ Buildings.Utilities.Math.Biquadratic

Biquadratic function

$Buildings.Utilities.Math.Biquadratic$

Information

This block computes

y = a₁ + a₂ x₁ + a₃ x₁² + a₄ x₂ + a₅ x₂² + a₆ x₁ x₂

Extends from Modelica.Blocks.Interfaces.SI2SO (2 Single Input / 1 Single Output continuous control block).

Parameters

Type	Name	Default	Description
Real	a[6]		Coefficients

Connectors

Type	Name	Description
input RealInput	u1	Connector of Real input signal 1
input RealInput	u2	Connector of Real input signal 2
output RealOutput	y	Connector of Real output signal

Modelica definition

block Biquadratic "Biquadratic function" extends Modelica.Blocks.Interfaces.SI2SO; parameter Real a[6] "Coefficients"; equation y = Buildings.Utilities.Math.Functions.biquadratic(a=a, x1=u1, x2=u2); end Biquadratic;

$Buildings.Utilities.Math.BooleanReplicator$ Buildings.Utilities.Math.BooleanReplicator

Boolean signal replicator

$Buildings.Utilities.Math.BooleanReplicator$

Information

This block replicates the boolean input signal to an array of nout identical output signals.

Extends from Modelica.Blocks.Icons.BooleanBlock (Basic graphical layout of Boolean block).

Parameters

Type	Name	Default	Description
Integer	nout	1	Number of outputs

Connectors

Type	Name	Description
input BooleanInput	u	Connector of boolean input signal
output BooleanOutput	y[nout]	Connector of boolean output signals

Modelica definition

block BooleanReplicator "Boolean signal replicator" extends Modelica.Blocks.Icons.BooleanBlock; parameter Integer nout=1 "Number of outputs"; Modelica.Blocks.Interfaces.BooleanInput u "Connector of boolean input signal"; Modelica.Blocks.Interfaces.BooleanOutput y[nout] "Connector of boolean output signals"; equation y = Buildings.Utilities.Math.Functions.booleanReplicator(u=u, nout=nout); end BooleanReplicator;

$Buildings.Utilities.Math.IntegerReplicator$ Buildings.Utilities.Math.IntegerReplicator

Integer signal replicator

$Buildings.Utilities.Math.IntegerReplicator$

Information

This block replicates the integer input signal to an array of nout identical output signals.

Extends from Modelica.Blocks.Icons.IntegerBlock (Basic graphical layout of Integer block).

Parameters

Type	Name	Default	Description
Integer	nout	1	Number of outputs

Connectors

Type	Name	Description
input IntegerInput	u	Connector of integer input signal
output IntegerOutput	y[nout]	Connector of integer output signals

Modelica definition

block IntegerReplicator "Integer signal replicator" extends Modelica.Blocks.Icons.IntegerBlock; parameter Integer nout=1 "Number of outputs"; Modelica.Blocks.Interfaces.IntegerInput u "Connector of integer input signal"; Modelica.Blocks.Interfaces.IntegerOutput y[nout] "Connector of integer output signals"; equation y = Buildings.Utilities.Math.Functions.integerReplicator(u=u, nout=nout); end IntegerReplicator;

$Buildings.Utilities.Math.InverseXRegularized$ Buildings.Utilities.Math.InverseXRegularized

Function that approximates 1/x by a twice continuously differentiable function

$Buildings.Utilities.Math.InverseXRegularized$

Information

Function that approximates y=1 ⁄ x inside the interval -δ ≤ x ≤ δ. The approximation is twice continuously differentiable with a bounded derivative on the whole real line.

See the package Examples for the graph.

Extends from Modelica.Blocks.Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Type	Name	Default	Description
Real	delta		Abscissa value below which approximation occurs

Connectors

Type	Name	Description
input RealInput	u	Connector of Real input signal
output RealOutput	y	Connector of Real output signal

Modelica definition

block InverseXRegularized "Function that approximates 1/x by a twice continuously differentiable function" extends Modelica.Blocks.Interfaces.SISO; parameter Real delta(min=0) "Abscissa value below which approximation occurs"; equation y = Buildings.Utilities.Math.Functions.inverseXRegularized(x=u, delta=delta); end InverseXRegularized;

$Buildings.Utilities.Math.Max$ Buildings.Utilities.Math.Max

Maximum element of a vector

$Buildings.Utilities.Math.Max$

Information

Outputs the maximum of the vector.

Extends from Modelica.Blocks.Interfaces.MISO (Multiple Input Single Output continuous control block).

Parameters

Type	Name	Default	Description
Integer	nin	1	Number of inputs

Connectors

Type	Name	Description
input RealInput	u[nin]	Connector of Real input signals
output RealOutput	y	Connector of Real output signal

Modelica definition

block Max "Maximum element of a vector" extends Modelica.Blocks.Interfaces.MISO; equation y = max(u); end Max;

$Buildings.Utilities.Math.Min$ Buildings.Utilities.Math.Min

Minimum element of a vector

$Buildings.Utilities.Math.Min$

Information

Outputs the minimum of the vector.

Extends from Modelica.Blocks.Interfaces.MISO (Multiple Input Single Output continuous control block).

Parameters

Type	Name	Default	Description
Integer	nin	1	Number of inputs

Connectors

Type	Name	Description
input RealInput	u[nin]	Connector of Real input signals
output RealOutput	y	Connector of Real output signal

Modelica definition

block Min "Minimum element of a vector" extends Modelica.Blocks.Interfaces.MISO; equation y = min(u); end Min;

$Buildings.Utilities.Math.Polynominal$ Buildings.Utilities.Math.Polynominal

Polynominal function

$Buildings.Utilities.Math.Polynominal$

Information

This block computes a polynomial of arbitrary order. The polynomial has the form

y = a1 + a2 x + a3 x2 + ...

Extends from Modelica.Blocks.Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Type	Name	Default	Description
Real	a[:]		Coefficients

Connectors

Type	Name	Description
input RealInput	u	Connector of Real input signal
output RealOutput	y	Connector of Real output signal

Modelica definition

block Polynominal "Polynominal function" extends Modelica.Blocks.Interfaces.SISO; parameter Real a[:] "Coefficients"; equation y = Buildings.Utilities.Math.Functions.polynomial(a=a, x=u); end Polynominal;

$Buildings.Utilities.Math.PowerLinearized$ Buildings.Utilities.Math.PowerLinearized

Power function that is linearized below a user-defined threshold

$Buildings.Utilities.Math.PowerLinearized$

Information

Function that approximates y=xⁿ where 0 < n so that

the function is defined and monotone increasing for all x.
dy/dx is bounded and continuous everywhere (for n < 1).

For x < x₀, this function replaces y=xⁿ by a linear function that is continuously differentiable everywhere.

A typical use of this function is to replace T = T4^(1/4) in a radiation balance to ensure that the function is defined everywhere. This can help solving the initialization problem when a solver may be far from a solution and hence T4 < 0.

See the package Examples for the graph.

Extends from Modelica.Blocks.Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Type	Name	Default	Description
Real	n		Exponent
Real	x0		Abscissa value below which linearization occurs

Connectors

Type	Name	Description
input RealInput	u	Connector of Real input signal
output RealOutput	y	Connector of Real output signal

Modelica definition

block PowerLinearized "Power function that is linearized below a user-defined threshold" extends Modelica.Blocks.Interfaces.SISO; parameter Real n "Exponent"; parameter Real x0 "Abscissa value below which linearization occurs"; equation y = Buildings.Utilities.Math.Functions.powerLinearized(x=u, n=n, x0=x0); end PowerLinearized;

$Buildings.Utilities.Math.QuadraticLinear$ Buildings.Utilities.Math.QuadraticLinear

Function that is quadratic in first argument and linear in second argument

$Buildings.Utilities.Math.QuadraticLinear$

Information

Block for function quadraticLinear, which computes

y = a1 + a2 x1 + a3 x12 + (a4 + a5 x1 + a6 x12) x2

Extends from Modelica.Blocks.Interfaces.SI2SO (2 Single Input / 1 Single Output continuous control block).

Parameters

Type	Name	Default	Description
Real	a[6]		Coefficients

Connectors

Type	Name	Description
input RealInput	u1	Connector of Real input signal 1
input RealInput	u2	Connector of Real input signal 2
output RealOutput	y	Connector of Real output signal

Modelica definition

block QuadraticLinear "Function that is quadratic in first argument and linear in second argument" extends Modelica.Blocks.Interfaces.SI2SO; parameter Real a[6] "Coefficients"; equation y = Buildings.Utilities.Math.Functions.quadraticLinear(a=a, x1=u1, x2=u2); end QuadraticLinear;

$Buildings.Utilities.Math.RegNonZeroPower$ Buildings.Utilities.Math.RegNonZeroPower

Power function, regularized near zero, but nonzero value for x=0

$Buildings.Utilities.Math.RegNonZeroPower$

Information

Function that approximates y=|x|ⁿ where n > 0 so that

y(0) is not equal to zero.
dy/dx is bounded and continuous everywhere.

This function replaces y=|x|ⁿ in the interval -δ...+δ by a 4-th order polynomial that has the same function value and the first and second derivative at x=± δ.

A typical use of this function is to replace the function for the convective heat transfer coefficient for forced or free convection that is of the form h=c |dT|ⁿ for some constant c and exponent 0 ≤ n ≤ 1. By using this function, the original function that has an infinite derivative near zero and that takes on zero at the origin is replaced by a function with a bounded derivative and a non-zero value at the origin. Physically, the region -δ...+δ may be interpreted as the region where heat conduction dominates convection in the boundary layer.

See the package Examples for the graph.

Extends from Modelica.Blocks.Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Type	Name	Default	Description
Real	n		Exponent
Real	delta	0.01	Abscissa value where transition occurs

Connectors

Type	Name	Description
input RealInput	u	Connector of Real input signal
output RealOutput	y	Connector of Real output signal

Modelica definition

block RegNonZeroPower "Power function, regularized near zero, but nonzero value for x=0" extends Modelica.Blocks.Interfaces.SISO; parameter Real n "Exponent"; parameter Real delta = 0.01 "Abscissa value where transition occurs"; equation y = Buildings.Utilities.Math.Functions.regNonZeroPower(x=u, n=n, delta=delta); end RegNonZeroPower;

$Buildings.Utilities.Math.SmoothExponential$ Buildings.Utilities.Math.SmoothExponential

Once continuously differentiable approximation to exp(-|x|) in interval |x| < delta

$Buildings.Utilities.Math.SmoothExponential$

Information

Function to provide a once continuously differentiable approximation to exp(- |x| ) in the interval |x| for some positive δ

Extends from Modelica.Blocks.Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Type	Name	Default	Description
Real	delta		Transition point where approximation occurs

Connectors

Type	Name	Description
input RealInput	u	Connector of Real input signal
output RealOutput	y	Connector of Real output signal

Modelica definition

block SmoothExponential "Once continuously differentiable approximation to exp(-|x|) in interval |x| < delta" extends Modelica.Blocks.Interfaces.SISO; parameter Real delta "Transition point where approximation occurs"; equation y = Buildings.Utilities.Math.Functions.smoothExponential(x=u, delta=delta); end SmoothExponential;

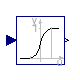$Buildings.Utilities.Math.SmoothHeaviside$ Buildings.Utilities.Math.SmoothHeaviside

Once continuously differentiable approximation to the Heaviside function

$Buildings.Utilities.Math.SmoothHeaviside$

Information

Once Lipschitz continuously differentiable approximation to the Heaviside(.,.) function.

Extends from Modelica.Blocks.Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Type	Name	Default	Description
Real	delta		Width of transition interval

Connectors

Type	Name	Description
input RealInput	u	Connector of Real input signal
output RealOutput	y	Connector of Real output signal

Modelica definition

block SmoothHeaviside "Once continuously differentiable approximation to the Heaviside function" extends Modelica.Blocks.Interfaces.SISO; parameter Real delta "Width of transition interval"; equation y = Buildings.Utilities.Math.Functions.smoothHeaviside(x=u, delta=delta); end SmoothHeaviside;

$Buildings.Utilities.Math.SmoothLimit$ Buildings.Utilities.Math.SmoothLimit

Once continuously differentiable approximation to the limit function

$Buildings.Utilities.Math.SmoothLimit$

Information

Once continuously differentiable approximation to the limit(.,.) function. The output is bounded to be in [lower, upper].

Note that the limit need not be respected, such as illustrated in Buildings.Utilities.Math.Examples.SmoothMin.

Extends from Modelica.Blocks.Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Type	Name	Description
Real	deltaX	Width of transition interval
Real	upper	Upper limit
Real	lower	Lower limit

Connectors

Type	Name	Description
input RealInput	u	Connector of Real input signal
output RealOutput	y	Connector of Real output signal

Modelica definition

block SmoothLimit "Once continuously differentiable approximation to the limit function" extends Modelica.Blocks.Interfaces.SISO; parameter Real deltaX "Width of transition interval"; parameter Real upper "Upper limit"; parameter Real lower "Lower limit"; equation y = Buildings.Utilities.Math.Functions.smoothLimit(u, lower, upper, deltaX); end SmoothLimit;

$Buildings.Utilities.Math.SmoothMax$ Buildings.Utilities.Math.SmoothMax

Once continuously differentiable approximation to the maximum function

$Buildings.Utilities.Math.SmoothMax$

Information

Once continuously differentiable approximation to the max(.,.) function.

Note that the maximum need not be respected, such as illustrated in Buildings.Utilities.Math.Examples.SmoothMin.

Extends from Modelica.Blocks.Interfaces.SI2SO (2 Single Input / 1 Single Output continuous control block).

Parameters

Type	Name	Default	Description
Real	deltaX		Width of transition interval

Connectors

Type	Name	Description
input RealInput	u1	Connector of Real input signal 1
input RealInput	u2	Connector of Real input signal 2
output RealOutput	y	Connector of Real output signal

Modelica definition

block SmoothMax "Once continuously differentiable approximation to the maximum function" extends Modelica.Blocks.Interfaces.SI2SO; parameter Real deltaX "Width of transition interval"; equation y = Buildings.Utilities.Math.Functions.smoothMax(x1=u1, x2=u2, deltaX=deltaX); end SmoothMax;

$Buildings.Utilities.Math.SmoothMin$ Buildings.Utilities.Math.SmoothMin

Once continuously differentiable approximation to the minimum function

$Buildings.Utilities.Math.SmoothMin$

Information

Once continuously differentiable approximation to the min(.,.) function.

Note that the minimum need not be respected, such as illustrated in Buildings.Utilities.Math.Examples.SmoothMin.

Extends from Modelica.Blocks.Interfaces.SI2SO (2 Single Input / 1 Single Output continuous control block).

Parameters

Type	Name	Default	Description
Real	deltaX		Width of transition interval

Connectors

Type	Name	Description
input RealInput	u1	Connector of Real input signal 1
input RealInput	u2	Connector of Real input signal 2
output RealOutput	y	Connector of Real output signal

Modelica definition

block SmoothMin "Once continuously differentiable approximation to the minimum function" extends Modelica.Blocks.Interfaces.SI2SO; parameter Real deltaX "Width of transition interval"; equation y = Buildings.Utilities.Math.Functions.smoothMin(x1=u1, x2=u2, deltaX=deltaX); end SmoothMin;

$Buildings.Utilities.Math.Splice$ Buildings.Utilities.Math.Splice

Block for splice function opertation

$Buildings.Utilities.Math.Splice$

Information

This block implements Buildings.Utilities.Math.Functions.spliceFunction, which provides a continuously differentiable transition between two arguments.

Extends from Modelica.Blocks.Icons.Block (Basic graphical layout of input/output block).

Parameters

Type	Name	Default	Description
Real	deltax		Half width of transition interval

Connectors

Type	Name	Description
input RealInput	x	Independent value
input RealInput	u1	Argument of u > 0 (pos)
input RealInput	u2	Argument of u < 0 (neg)
output RealOutput	y	Smoothed value

Modelica definition

block Splice "Block for splice function opertation" extends Modelica.Blocks.Icons.Block; Modelica.Blocks.Interfaces.RealInput x "Independent value"; Modelica.Blocks.Interfaces.RealInput u1 "Argument of u > 0 (pos)"; Modelica.Blocks.Interfaces.RealInput u2 "Argument of u < 0 (neg)"; Modelica.Blocks.Interfaces.RealOutput y "Smoothed value"; parameter Real deltax "Half width of transition interval"; equation y=Buildings.Utilities.Math.Functions.spliceFunction( pos=u1, neg= u2, x= x, deltax= deltax); end Splice;

$Buildings.Utilities.Math.TrapezoidalIntegration$ Buildings.Utilities.Math.TrapezoidalIntegration

Integration using the trapezoidal rule

$Buildings.Utilities.Math.TrapezoidalIntegration$

Information

This function computes a definite integral using the trapezoidal rule.

Extends from Modelica.Blocks.Interfaces.MISO (Multiple Input Single Output continuous control block).

Parameters

Type	Name	Default	Description
Integer	nin	1	Number of inputs
Integer	N		Number of integrand points
Real	deltaX		Width of interval for Trapezoidal integration

Connectors

Type	Name	Description
input RealInput	u[nin]	Connector of Real input signals
output RealOutput	y	Connector of Real output signal

Modelica definition

model TrapezoidalIntegration "Integration using the trapezoidal rule" extends Modelica.Blocks.Interfaces.MISO; parameter Integer N "Number of integrand points"; parameter Real deltaX "Width of interval for Trapezoidal integration"; equation y = Buildings.Utilities.Math.Functions.trapezoidalIntegration(N=N, f=u, deltaX=deltaX); end TrapezoidalIntegration;

Automatically generated Mon Jul 13 14:30:45 2015.