

Package with chiller models
Extends from Modelica.Icons.VariantsPackage (Icon for package containing variants).
| Name | Description |
|---|---|
| Chiller with performance curve adjusted based on Carnot efficiency | |
| Electric chiller based on the DOE-2.1 model | |
| Electric chiller based on the DOE-2.1 model, but with performance as a function of condenser leaving instead of entering temperature | |
| Performance data for electric chillers | |
| Collection of models that illustrate model use and test models | |
| Package with base classes for Buildings.Fluid.Chillers |
 Buildings.Fluid.Chillers.Carnot
Buildings.Fluid.Chillers.Carnot
Chiller with performance curve adjusted based on Carnot efficiency
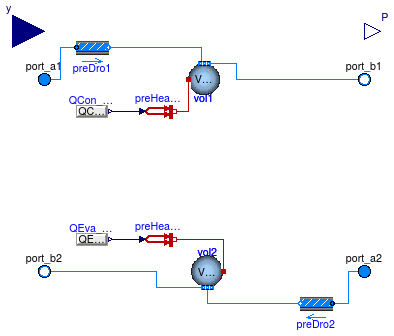
This is model of a chiller whose coefficient of performance (COP) changes with temperatures in the same way as the Carnot efficiency changes. The COP at the nominal conditions can be specified by a parameter, or it can be computed by the model based on the Carnot effectiveness, in which case
COP0 = ηcar COPcar = ηcar Teva ⁄ (Tcon-Teva),
where Teva is the evaporator temperature
and Tcon is the condenser temperature.
On the Advanced tab, a user can specify the temperature that
will be used as the evaporator (or condenser) temperature. The options
are the temperature of the fluid volume, of port_a, of
port_b, or the average temperature of port_a and
port_b.
The chiller COP is computed as the product
COP = ηcar COPcar ηPL,
where ηcar is the Carnot effectiveness, COPcar is the Carnot efficiency and ηPL is a polynomial in the control signal y that can be used to take into account a change in COP at part load conditions.
On the Dynamics tag, the model can be parametrized to compute a transient
or steady-state response.
The transient response of the model is computed using a first
order differential equation for the evaporator and condenser fluid volumes.
The chiller outlet temperatures are equal to the temperatures of these lumped volumes.
Extends from Interfaces.FourPortHeatMassExchanger (Model transporting two fluid streams between four ports with storing mass or energy).
| Type | Name | Default | Description |
|---|---|---|---|
| replaceable package Medium1 | PartialMedium | Medium 1 in the component | |
| replaceable package Medium2 | PartialMedium | Medium 2 in the component | |
| Nominal condition | |||
| MassFlowRate | m1_flow_nominal | Nominal mass flow rate [kg/s] | |
| MassFlowRate | m2_flow_nominal | Nominal mass flow rate [kg/s] | |
| Pressure | dp1_nominal | Pressure difference [Pa] | |
| Pressure | dp2_nominal | Pressure difference [Pa] | |
| Power | P_nominal | Nominal compressor power (at y=1) [W] | |
| TemperatureDifference | dTEva_nominal | 10 | Temperature difference evaporator inlet-outlet [K] |
| TemperatureDifference | dTCon_nominal | 10 | Temperature difference condenser outlet-inlet [K] |
| Initialization | |||
| MassFlowRate | m1_flow.start | 0 | Mass flow rate from port_a1 to port_b1 (m1_flow > 0 is design flow direction) [kg/s] |
| Pressure | dp1.start | 0 | Pressure difference between port_a1 and port_b1 [Pa] |
| MassFlowRate | m2_flow.start | 0 | Mass flow rate from port_a2 to port_b2 (m2_flow > 0 is design flow direction) [kg/s] |
| Pressure | dp2.start | 0 | Pressure difference between port_a2 and port_b2 [Pa] |
| Efficiency | |||
| Boolean | use_eta_Carnot | true | Set to true to use Carnot efficiency |
| Real | etaCar | Carnot effectiveness (=COP/COP_Carnot) | |
| Real | COP_nominal | Coefficient of performance | |
| Temperature | TCon_nominal | 303.15 | Condenser temperature [K] |
| Temperature | TEva_nominal | 278.15 | Evaporator temperature [K] |
| Real | a[:] | {1} | Coefficients for efficiency curve (need p(a=a, y=1)=1) |
| Assumptions | |||
| Boolean | allowFlowReversal1 | true | = true to allow flow reversal in medium 1, false restricts to design direction (port_a -> port_b) |
| Boolean | allowFlowReversal2 | true | = true to allow flow reversal in medium 2, false restricts to design direction (port_a -> port_b) |
| Advanced | |||
| MassFlowRate | m1_flow_small | 1E-4*abs(m1_flow_nominal) | Small mass flow rate for regularization of zero flow [kg/s] |
| MassFlowRate | m2_flow_small | 1E-4*abs(m2_flow_nominal) | Small mass flow rate for regularization of zero flow [kg/s] |
| Boolean | homotopyInitialization | true | = true, use homotopy method |
| Diagnostics | |||
| Boolean | show_T | false | = true, if actual temperature at port is computed |
| Temperature dependence | |||
| EfficiencyInput | effInpEva | Buildings.Fluid.Types.Effici... | Temperatures of evaporator fluid used to compute Carnot efficiency |
| EfficiencyInput | effInpCon | Buildings.Fluid.Types.Effici... | Temperatures of condenser fluid used to compute Carnot efficiency |
| Flow resistance | |||
| Medium 1 | |||
| Boolean | from_dp1 | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | linearizeFlowResistance1 | false | = true, use linear relation between m_flow and dp for any flow rate |
| Real | deltaM1 | 0.1 | Fraction of nominal flow rate where flow transitions to laminar |
| Medium 2 | |||
| Boolean | from_dp2 | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | linearizeFlowResistance2 | false | = true, use linear relation between m_flow and dp for any flow rate |
| Real | deltaM2 | 0.1 | Fraction of nominal flow rate where flow transitions to laminar |
| Dynamics | |||
| Nominal condition | |||
| Time | tau1 | 30 | Time constant at nominal flow [s] |
| Time | tau2 | 30 | Time constant at nominal flow [s] |
| Equations | |||
| Dynamics | energyDynamics | Modelica.Fluid.Types.Dynamic... | Formulation of energy balance |
| Dynamics | massDynamics | energyDynamics | Formulation of mass balance |
| Initialization | |||
| Medium 1 | |||
| AbsolutePressure | p1_start | Medium1.p_default | Start value of pressure [Pa] |
| Temperature | T1_start | Medium1.T_default | Start value of temperature [K] |
| MassFraction | X1_start[Medium1.nX] | Medium1.X_default | Start value of mass fractions m_i/m [kg/kg] |
| ExtraProperty | C1_start[Medium1.nC] | fill(0, Medium1.nC) | Start value of trace substances |
| ExtraProperty | C1_nominal[Medium1.nC] | fill(1E-2, Medium1.nC) | Nominal value of trace substances. (Set to typical order of magnitude.) |
| Medium 2 | |||
| AbsolutePressure | p2_start | Medium2.p_default | Start value of pressure [Pa] |
| Temperature | T2_start | Medium2.T_default | Start value of temperature [K] |
| MassFraction | X2_start[Medium2.nX] | Medium2.X_default | Start value of mass fractions m_i/m [kg/kg] |
| ExtraProperty | C2_start[Medium2.nC] | fill(0, Medium2.nC) | Start value of trace substances |
| ExtraProperty | C2_nominal[Medium2.nC] | fill(1E-2, Medium2.nC) | Nominal value of trace substances. (Set to typical order of magnitude.) |
| Type | Name | Description |
|---|---|---|
| FluidPort_a | port_a1 | Fluid connector a1 (positive design flow direction is from port_a1 to port_b1) |
| FluidPort_b | port_b1 | Fluid connector b1 (positive design flow direction is from port_a1 to port_b1) |
| FluidPort_a | port_a2 | Fluid connector a2 (positive design flow direction is from port_a2 to port_b2) |
| FluidPort_b | port_b2 | Fluid connector b2 (positive design flow direction is from port_a2 to port_b2) |
| input RealInput | y | Part load ratio |
| output RealOutput | P | Electric power consumed by compressor [W] |
 Buildings.Fluid.Chillers.ElectricEIR
Buildings.Fluid.Chillers.ElectricEIR
Electric chiller based on the DOE-2.1 model
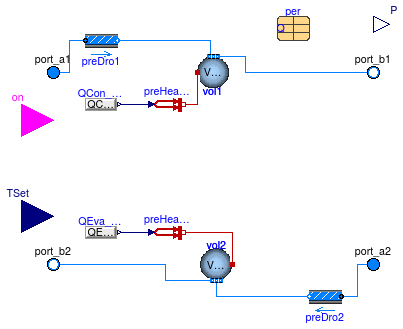
Model of an electric chiller, based on the DOE-2.1 chiller model and
the EnergyPlus chiller model Chiller:Electric:EIR.
This model uses three functions to predict capacity and power consumption:
These curves are stored in the data record per and are available from
Buildings.Fluid.Chillers.Data.ElectricEIR.
Additional performance curves can be developed using
two available techniques (Hydeman and Gillespie, 2002). The first technique is called the
Least-squares Linear Regression method and is used when sufficient performance data exist
to employ standard least-square linear regression techniques. The second technique is called
Reference Curve Method and is used when insufficient performance data exist to apply linear
regression techniques. A detailed description of both techniques can be found in
Hydeman and Gillespie (2002).
The model takes as an input the set point for the leaving chilled water temperature, which is met if the chiller has sufficient capacity. Thus, the model has a built-in, ideal temperature control. The model has three tests on the part load ratio and the cycling ratio:
PLR1 =min(QEva_flow_set/QEva_flow_ava, per.PLRMax);ensures that the chiller capacity does not exceed the chiller capacity specified by the parameter
per.PLRMax.
CR = min(PLR1/per.PRLMin, 1.0);computes a cycling ratio. This ratio expresses the fraction of time that a chiller would run if it were to cycle because its load is smaller than the minimal load at which it can operate. Note that this model continuously operates even if the part load ratio is below the minimum part load ratio. Its leaving evaporator and condenser temperature can therefore be considered as an average temperature between the modes where the compressor is off and on.
PLR2 = max(per.PLRMinUnl, PLR1);computes the part load ratio of the compressor. The assumption is that for a part load ratio below
per.PLRMinUnl,
the chiller uses hot gas bypass to reduce the capacity, while the compressor
power draw does not change.
The electric power only contains the power for the compressor, but not any power for pumps or fans.
The model can be parametrized to compute a transient or steady-state response. The transient response of the boiler is computed using a first order differential equation for the evaporator and condenser fluid volumes. The chiller outlet temperatures are equal to the temperatures of these lumped volumes.
Extends from Buildings.Fluid.Chillers.BaseClasses.PartialElectric (Partial model for electric chiller based on the model in DOE-2, CoolTools and EnergyPlus).
| Type | Name | Default | Description |
|---|---|---|---|
| replaceable package Medium1 | PartialMedium | Medium 1 in the component | |
| replaceable package Medium2 | PartialMedium | Medium 2 in the component | |
| Generic | per | Performance data | |
| Nominal condition | |||
| MassFlowRate | m1_flow_nominal | mCon_flow_nominal | Nominal mass flow rate [kg/s] |
| MassFlowRate | m2_flow_nominal | mEva_flow_nominal | Nominal mass flow rate [kg/s] |
| Pressure | dp1_nominal | Pressure difference [Pa] | |
| Pressure | dp2_nominal | Pressure difference [Pa] | |
| Initialization | |||
| MassFlowRate | m1_flow.start | 0 | Mass flow rate from port_a1 to port_b1 (m1_flow > 0 is design flow direction) [kg/s] |
| Pressure | dp1.start | 0 | Pressure difference between port_a1 and port_b1 [Pa] |
| MassFlowRate | m2_flow.start | 0 | Mass flow rate from port_a2 to port_b2 (m2_flow > 0 is design flow direction) [kg/s] |
| Pressure | dp2.start | 0 | Pressure difference between port_a2 and port_b2 [Pa] |
| Real | capFunT.start | 1 | Cooling capacity factor function of temperature curve [1] |
| Real | EIRFunT.start | 1 | Power input to cooling capacity ratio function of temperature curve [1] |
| Real | EIRFunPLR.start | 1 | Power input to cooling capacity ratio function of part load ratio [1] |
| Real | PLR1.start | 1 | Part load ratio [1] |
| Real | PLR2.start | 1 | Part load ratio [1] |
| Real | CR.start | 1 | Cycling ratio [1] |
| Assumptions | |||
| Boolean | allowFlowReversal1 | true | = true to allow flow reversal in medium 1, false restricts to design direction (port_a -> port_b) |
| Boolean | allowFlowReversal2 | true | = true to allow flow reversal in medium 2, false restricts to design direction (port_a -> port_b) |
| Advanced | |||
| MassFlowRate | m1_flow_small | 1E-4*abs(m1_flow_nominal) | Small mass flow rate for regularization of zero flow [kg/s] |
| MassFlowRate | m2_flow_small | 1E-4*abs(m2_flow_nominal) | Small mass flow rate for regularization of zero flow [kg/s] |
| Boolean | homotopyInitialization | true | = true, use homotopy method |
| Diagnostics | |||
| Boolean | show_T | false | = true, if actual temperature at port is computed |
| Flow resistance | |||
| Medium 1 | |||
| Boolean | from_dp1 | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | linearizeFlowResistance1 | false | = true, use linear relation between m_flow and dp for any flow rate |
| Real | deltaM1 | 0.1 | Fraction of nominal flow rate where flow transitions to laminar |
| Medium 2 | |||
| Boolean | from_dp2 | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | linearizeFlowResistance2 | false | = true, use linear relation between m_flow and dp for any flow rate |
| Real | deltaM2 | 0.1 | Fraction of nominal flow rate where flow transitions to laminar |
| Dynamics | |||
| Nominal condition | |||
| Time | tau1 | 30 | Time constant at nominal flow [s] |
| Time | tau2 | 30 | Time constant at nominal flow [s] |
| Equations | |||
| Dynamics | energyDynamics | Modelica.Fluid.Types.Dynamic... | Formulation of energy balance |
| Dynamics | massDynamics | energyDynamics | Formulation of mass balance |
| Initialization | |||
| Medium 1 | |||
| AbsolutePressure | p1_start | Medium1.p_default | Start value of pressure [Pa] |
| Temperature | T1_start | 273.15 + 25 | Start value of temperature [K] |
| MassFraction | X1_start[Medium1.nX] | Medium1.X_default | Start value of mass fractions m_i/m [kg/kg] |
| ExtraProperty | C1_start[Medium1.nC] | fill(0, Medium1.nC) | Start value of trace substances |
| ExtraProperty | C1_nominal[Medium1.nC] | fill(1E-2, Medium1.nC) | Nominal value of trace substances. (Set to typical order of magnitude.) |
| Medium 2 | |||
| AbsolutePressure | p2_start | Medium2.p_default | Start value of pressure [Pa] |
| Temperature | T2_start | 273.15 + 5 | Start value of temperature [K] |
| MassFraction | X2_start[Medium2.nX] | Medium2.X_default | Start value of mass fractions m_i/m [kg/kg] |
| ExtraProperty | C2_start[Medium2.nC] | fill(0, Medium2.nC) | Start value of trace substances |
| ExtraProperty | C2_nominal[Medium2.nC] | fill(1E-2, Medium2.nC) | Nominal value of trace substances. (Set to typical order of magnitude.) |
| Type | Name | Description |
|---|---|---|
| FluidPort_a | port_a1 | Fluid connector a1 (positive design flow direction is from port_a1 to port_b1) |
| FluidPort_b | port_b1 | Fluid connector b1 (positive design flow direction is from port_a1 to port_b1) |
| FluidPort_a | port_a2 | Fluid connector a2 (positive design flow direction is from port_a2 to port_b2) |
| FluidPort_b | port_b2 | Fluid connector b2 (positive design flow direction is from port_a2 to port_b2) |
| input BooleanInput | on | Set to true to enable compressor, or false to disable compressor |
| input RealInput | TSet | Set point for leaving chilled water temperature [K] |
| output RealOutput | P | Electric power consumed by compressor [W] |
 Buildings.Fluid.Chillers.ElectricReformulatedEIR
Buildings.Fluid.Chillers.ElectricReformulatedEIR
Electric chiller based on the DOE-2.1 model, but with performance as a function of condenser leaving instead of entering temperature

Model of an electric chiller, based on the model by
Hydeman et al. (2002) that has been developed in the CoolTools project
and that is implemented in EnergyPlus as the model
Chiller:Electric:ReformulatedEIR.
This empirical model is similar to
Buildings.Fluid.Chillers.ElectricEIR.
The difference is that to compute the performance, this model
uses the condenser leaving temperature instead of the entering temperature,
and it uses a bicubic polynomial to compute the part load performance.
This model uses three functions to predict capacity and power consumption:
These curves are stored in the data record per and are available from
Buildings.Fluid.Chillers.Data.ElectricReformulatedEIRChiller.
Additional performance curves can be developed using
two available techniques (Hydeman and Gillespie, 2002). The first technique is called the
Least-squares Linear Regression method and is used when sufficient performance data exist
to employ standard least-square linear regression techniques. The second technique is called
Reference Curve Method and is used when insufficient performance data exist to apply linear
regression techniques. A detailed description of both techniques can be found in
Hydeman and Gillespie (2002).
The model takes as an input the set point for the leaving chilled water temperature, which is met if the chiller has sufficient capacity. Thus, the model has a built-in, ideal temperature control. The model has three tests on the part load ratio and the cycling ratio:
PLR1 =min(QEva_flow_set/QEva_flow_ava, per.PLRMax);ensures that the chiller capacity does not exceed the chiller capacity specified by the parameter
per.PLRMax.
CR = min(PLR1/per.PRLMin, 1.0);computes a cycling ratio. This ratio expresses the fraction of time that a chiller would run if it were to cycle because its load is smaller than the minimal load at which it can operate. Note that this model continuously operates even if the part load ratio is below the minimum part load ratio. Its leaving evaporator and condenser temperature can therefore be considered as an average temperature between the modes where the compressor is off and on.
PLR2 = max(per.PLRMinUnl, PLR1);computes the part load ratio of the compressor. The assumption is that for a part load ratio below
per.PLRMinUnl,
the chiller uses hot gas bypass to reduce the capacity, while the compressor
power draw does not change.
The electric power only contains the power for the compressor, but not any power for pumps or fans.
The model can be parametrized to compute a transient or steady-state response. The transient response of the boiler is computed using a first order differential equation for the evaporator and condenser fluid volumes. The chiller outlet temperatures are equal to the temperatures of these lumped volumes.
Extends from Buildings.Fluid.Chillers.BaseClasses.PartialElectric (Partial model for electric chiller based on the model in DOE-2, CoolTools and EnergyPlus).
| Type | Name | Default | Description |
|---|---|---|---|
| replaceable package Medium1 | PartialMedium | Medium 1 in the component | |
| replaceable package Medium2 | PartialMedium | Medium 2 in the component | |
| Generic | per | Performance data | |
| Nominal condition | |||
| MassFlowRate | m1_flow_nominal | mCon_flow_nominal | Nominal mass flow rate [kg/s] |
| MassFlowRate | m2_flow_nominal | mEva_flow_nominal | Nominal mass flow rate [kg/s] |
| Pressure | dp1_nominal | Pressure difference [Pa] | |
| Pressure | dp2_nominal | Pressure difference [Pa] | |
| Initialization | |||
| MassFlowRate | m1_flow.start | 0 | Mass flow rate from port_a1 to port_b1 (m1_flow > 0 is design flow direction) [kg/s] |
| Pressure | dp1.start | 0 | Pressure difference between port_a1 and port_b1 [Pa] |
| MassFlowRate | m2_flow.start | 0 | Mass flow rate from port_a2 to port_b2 (m2_flow > 0 is design flow direction) [kg/s] |
| Pressure | dp2.start | 0 | Pressure difference between port_a2 and port_b2 [Pa] |
| Real | capFunT.start | 1 | Cooling capacity factor function of temperature curve [1] |
| Real | EIRFunT.start | 1 | Power input to cooling capacity ratio function of temperature curve [1] |
| Real | EIRFunPLR.start | 1 | Power input to cooling capacity ratio function of part load ratio [1] |
| Real | PLR1.start | 1 | Part load ratio [1] |
| Real | PLR2.start | 1 | Part load ratio [1] |
| Real | CR.start | 1 | Cycling ratio [1] |
| Assumptions | |||
| Boolean | allowFlowReversal1 | true | = true to allow flow reversal in medium 1, false restricts to design direction (port_a -> port_b) |
| Boolean | allowFlowReversal2 | true | = true to allow flow reversal in medium 2, false restricts to design direction (port_a -> port_b) |
| Advanced | |||
| MassFlowRate | m1_flow_small | 1E-4*abs(m1_flow_nominal) | Small mass flow rate for regularization of zero flow [kg/s] |
| MassFlowRate | m2_flow_small | 1E-4*abs(m2_flow_nominal) | Small mass flow rate for regularization of zero flow [kg/s] |
| Boolean | homotopyInitialization | true | = true, use homotopy method |
| Diagnostics | |||
| Boolean | show_T | false | = true, if actual temperature at port is computed |
| Flow resistance | |||
| Medium 1 | |||
| Boolean | from_dp1 | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | linearizeFlowResistance1 | false | = true, use linear relation between m_flow and dp for any flow rate |
| Real | deltaM1 | 0.1 | Fraction of nominal flow rate where flow transitions to laminar |
| Medium 2 | |||
| Boolean | from_dp2 | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | linearizeFlowResistance2 | false | = true, use linear relation between m_flow and dp for any flow rate |
| Real | deltaM2 | 0.1 | Fraction of nominal flow rate where flow transitions to laminar |
| Dynamics | |||
| Nominal condition | |||
| Time | tau1 | 30 | Time constant at nominal flow [s] |
| Time | tau2 | 30 | Time constant at nominal flow [s] |
| Equations | |||
| Dynamics | energyDynamics | Modelica.Fluid.Types.Dynamic... | Formulation of energy balance |
| Dynamics | massDynamics | energyDynamics | Formulation of mass balance |
| Initialization | |||
| Medium 1 | |||
| AbsolutePressure | p1_start | Medium1.p_default | Start value of pressure [Pa] |
| Temperature | T1_start | 273.15 + 25 | Start value of temperature [K] |
| MassFraction | X1_start[Medium1.nX] | Medium1.X_default | Start value of mass fractions m_i/m [kg/kg] |
| ExtraProperty | C1_start[Medium1.nC] | fill(0, Medium1.nC) | Start value of trace substances |
| ExtraProperty | C1_nominal[Medium1.nC] | fill(1E-2, Medium1.nC) | Nominal value of trace substances. (Set to typical order of magnitude.) |
| Medium 2 | |||
| AbsolutePressure | p2_start | Medium2.p_default | Start value of pressure [Pa] |
| Temperature | T2_start | 273.15 + 5 | Start value of temperature [K] |
| MassFraction | X2_start[Medium2.nX] | Medium2.X_default | Start value of mass fractions m_i/m [kg/kg] |
| ExtraProperty | C2_start[Medium2.nC] | fill(0, Medium2.nC) | Start value of trace substances |
| ExtraProperty | C2_nominal[Medium2.nC] | fill(1E-2, Medium2.nC) | Nominal value of trace substances. (Set to typical order of magnitude.) |
| Type | Name | Description |
|---|---|---|
| FluidPort_a | port_a1 | Fluid connector a1 (positive design flow direction is from port_a1 to port_b1) |
| FluidPort_b | port_b1 | Fluid connector b1 (positive design flow direction is from port_a1 to port_b1) |
| FluidPort_a | port_a2 | Fluid connector a2 (positive design flow direction is from port_a2 to port_b2) |
| FluidPort_b | port_b2 | Fluid connector b2 (positive design flow direction is from port_a2 to port_b2) |
| input BooleanInput | on | Set to true to enable compressor, or false to disable compressor |
| input RealInput | TSet | Set point for leaving chilled water temperature [K] |
| output RealOutput | P | Electric power consumed by compressor [W] |