Buildings.Fluid.HeatExchangers.Boreholes.BaseClasses

Base classes for Borehole

Information

This package contains base classes that are used to construct the models in Buildings.Fluid.HeatExchangers.Boreholes.

Extends from Modelica.Icons.BasesPackage (Icon for packages containing base classes).

Package Content

Name	Description
BoreholeSegment	Vertical segment of a borehole
ExtendableArray	class used to create the external object: ExtendableArray
HexInternalElement	Internal part of a borehole
SingleUTubeBoundaryCondition	Prescribed temperature at the outer boundary of a single U tube borehole
convectionResistance	Thermal resistance between the fluid and the tube
exchangeValues	Store the value u at the element n in the external object, and return the value of the element i
factorial	Calculates the factorial value of the input
powerSeries	Power series used to compute far-field temperature
singleUTubeResistances	Thermal resistances for single U-tube
temperatureDrop	Calculate the temperature drop of the soil at the external boundary of the cylinder
Examples	Example models to test base classes

Buildings.Fluid.HeatExchangers.Boreholes.BaseClasses.BoreholeSegment

Vertical segment of a borehole

Information

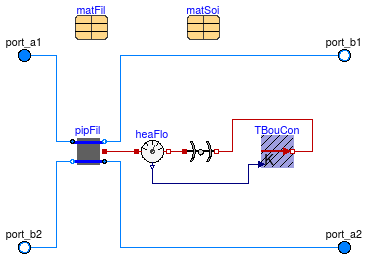
Horizontal layer that is used to model a U-tube borehole heat exchanger. This model combines three models, each simulating a different aspect of a borehole heat exchanger.

The instance pipFil computes the heat transfer in the pipes and the filling material. This computation is done using the model Buildings.Fluid.HeatExchangers.Boreholes.BaseClasses.HexInternalElement.

The instance soi computes transient and steady state heat transfer in the soil using a vertical cylinder. The computation is done using the model Buildings.HeatTransfer.Conduction.SingleLayerCylinder.

The model TBouCon computes the far-field temperature boundary condition, i.e., the temperature at the outer surface of the above cylindrical heat transfer computation. The computation is done using the model Buildings.Fluid.HeatExchangers.Boreholes.BaseClasses.SingleUTubeBoundaryCondition.

Extends from Buildings.Fluid.Interfaces.PartialFourPortInterface (Partial model transporting fluid between two ports without storing mass or energy), Buildings.Fluid.Interfaces.TwoPortFlowResistanceParameters (Parameters for flow resistance for models with two ports), Buildings.Fluid.Interfaces.LumpedVolumeDeclarations (Declarations for lumped volumes).

Parameters

Connectors

Modelica definition

Buildings.Fluid.HeatExchangers.Boreholes.BaseClasses.ExtendableArray

class used to create the external object: ExtendableArray

Information

Class derived from ExternalObject having two local external function definition, named destructor and constructor respectively.

These functions create and release an external object that allows the storage of real parameters in an array of extendable dimension.

Extends from ExternalObject.

Modelica definition

Buildings.Fluid.HeatExchangers.Boreholes.BaseClasses.HexInternalElement

Internal part of a borehole

Information

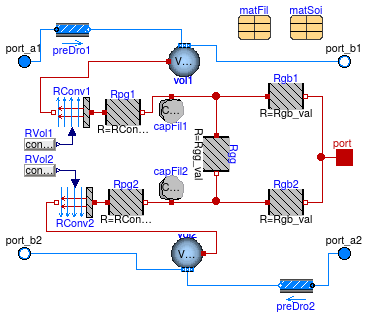
Model for the heat transfer between the fluid and within the borehole filling. This model computes the dynamic response of the fluid in the tubes, the heat transfer between the fluid and the borehole filling, and the heat storage within the fluid and the borehole filling.

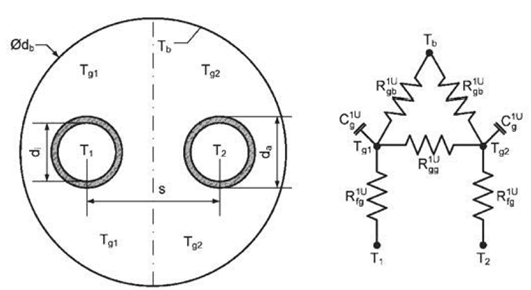
This model computes the different thermal resistances present in a single-U-tube borehole using the method of Bauer et al. (2011) and computing explicitly the fluid-to-ground thermal resistance R_b and the grout-to-grout resistance R_a as defined by Hellstroem (1991) using the multipole method. The multipole method is implemented in Buildings.Fluid.HeatExchangers.Boreholes.BaseClasses.singleUTubeResistances. The convection resistance is calculated using the Dittus-Boelter correlation as implemented in Buildings.Fluid.HeatExchangers.Boreholes.BaseClasses.convectionResistance.

The figure below shows the thermal network set up by Bauer et al. (2010).

References

G. Hellström. Ground heat storage: thermal analyses of duct storage systems (Theory). Dept. of Mathematical Physics, University of Lund, Sweden, 1991.

D. Bauer, W. Heidemann, H. Müller-Steinhagen, and H.-J. G. Diersch. Thermal resistance and capacity models for borehole heat exchangers . International Journal Of Energy Research, 35:312–320, 2011.

Extends from Buildings.Fluid.Interfaces.FourPortHeatMassExchanger (Model transporting two fluid streams between four ports with storing mass or energy).

Parameters

Connectors

Modelica definition

Buildings.Fluid.HeatExchangers.Boreholes.BaseClasses.SingleUTubeBoundaryCondition

Prescribed temperature at the outer boundary of a single U tube borehole

Information

This model computes the temperature boundary condition at the outer boundary of the borehole. It takes as an input the heat flow rate at the center of the borehole. This heat flow rate is averaged over the sample period. At each sampling interval, typically every one week, a new temperature boundary conditions is computed using the analytical solution to a line source heat transfer problem.

Implementation

The computation of the temperature change of the boundary is computed using the function Buildings.Fluid.HeatExchangers.Boreholes.BaseClasses.temperatureDrop.

Parameters

Connectors

Modelica definition

Buildings.Fluid.HeatExchangers.Boreholes.BaseClasses.convectionResistance

Thermal resistance between the fluid and the tube

Information

This model computes the convection resistance in the pipes of a borehole segment with heigth h_Seg.

The correlation of Dittus-Boelter (1930) is used to find the convection heat transfer coefficient as

Nu = 0.023   Re^0.8   Prⁿ,

where Nu is the Nusselt number, Re is the Reynolds number and Pr is the Prandlt number. We selected n=0.35, as the reference uses n=0.4 for heating and n=0.3 for cooling. Dittus-Boelter's correlation is valid for turbulent flow in cylindrical smooth pipe.

References

Dittus P.W. and L.M.K Boelter, (1930). Heat transfer in automobile radiators of the tubular type. Univ Calif Pub Eng, 2(13):443-461. (Reprinted in Int. J. Comm. Heat Mass Transf. 12 (1985), 3:22). DOI:10.1016/0735-1933(85)90003-X.

Inputs

Outputs

Modelica definition

Buildings.Fluid.HeatExchangers.Boreholes.BaseClasses.exchangeValues

Store the value u at the element n in the external object, and return the value of the element i

Information

External function that stores the input value x as the element a[iX] in the array a = [a[1], a[2], ...], and that returns the element a[iY]. The size of the array a is automatically enlarged as needed.

Inputs

Outputs

Modelica definition

Buildings.Fluid.HeatExchangers.Boreholes.BaseClasses.factorial

Calculates the factorial value of the input

Information

This function computes y = j!.

Inputs

Outputs

Modelica definition

Buildings.Fluid.HeatExchangers.Boreholes.BaseClasses.powerSeries

Power series used to compute far-field temperature

Information

This function computes the power series that is used to compute the far-field temperature.

Inputs

Outputs

Modelica definition

Buildings.Fluid.HeatExchangers.Boreholes.BaseClasses.singleUTubeResistances

Thermal resistances for single U-tube

Information

This model computes the thermal resistances of a single-U-tube borehole using the method of Bauer et al. (2011). It also computes the fluid-to-ground thermal resistance R_b and the grout-to-grout thermal resistance R_a as defined by Hellstroem (1991) using the multipole method.

The figure below shows the thermal network set up by Bauer et al. (2011).

The different resistances are calculated as follows. The grout zone and bore hole wall thermal resistance are related as

R_gb^1U = ( 1 - x^1U ) R_g^1U.

The thermal resistance between the two grout zones are

R_gg^1U = 2 R_gb^1U ( R_ar^1U - 2 x^1U R_g^1U ) / ( 2 R_gb^1U - R_ar^1U + 2 x^1U R_g^1U ).

Thermal resistance between the pipe wall to the capacity in the grout is

R_CondGro = x^1U R_g^1U + log ( ( r_Tub + e_Tub ) /r_Tub ) / ( 2 π h_Seg k_Tub ).

The capacities are located at

x^1U =log ( (r_Bor² + 2 ( r_Tub + e_Tub ) ²)^1⁄2/ ( 2 ( r_Tub + e_Tub ) ) ) / log ( r_Bor/ ( √2 ( r_Tub + e_Tub ))).

The thermal resistance between the outer borehole wall and one tube is

R_g^1U =2 R_b ⁄ h_Seg.

The thermal resistance between the two pipe outer walls is

R_ar^1U =R_a ⁄ h_Seg.

The fluid to ground thermal resistance R_b and the grout to grout thermal resistance R_a are calculated with the multipole method (Hellstroem (1991)) as

R_b =1/ ( 4 π k_Fil ) ( log ( r_Bor/ ( r_Tub + e_Tub ) ) + log ( r_Bor/ ( 2 x_C ) ) + σ log ( r_Bor⁴/ ( r_Bor⁴ - x_C⁴ ) ) ) - 1/ ( 4 π k_Fil ) ( ( r_Tub + e_Tub ) ²/ ( 4 x_C² ) ( 1 - σ 4 x_C⁴/ ( r_Bor⁴ - x_C⁴ ) ) ² ) / ( ( 1 + β ) / ( 1 - β ) + ( r_Tub + e_Tub ) ²/ ( 4 x_C² ) ( 1 + σ 16 x_C⁴ r_Bor⁴/ ( r_Bor⁴ - x_C⁴ ) ²)).

R_a = 1/ ( π k_Fil ) ( log ( 2 x_C/r_Tub ) + σ log (( r_Bor² + x_C² ) / ( r_Bor² - x_C² ) ) ) - 1/ ( π k_Fil ) ( r_Tub²/ ( 4 x_C² ) ( 1 + σ 4 r_Bor⁴ x_C²/ ( r_Bor⁴ - x_C⁴ ) ) / ( ( 1 + β ) / ( 1 - β ) - r_Tub²/ ( 4 x_C² ) + σ 2 r_Tub² r_Bor² ( r_Bor⁴ + x_C⁴ ) / ( r_Bor⁴ - x_C⁴ ) ²)),

with σ = ( k_Fil - k_Soi ) / ( k_Fil + k_Soi ) and β = 2 π k_Fil R_CondPipe, where k_Fil and k_Soi are the conductivity of the filling material and of the ground, r_Tub+e_Tub and r_Bor are the pipe and the borehole outside radius and x_C is the shank spacing, which is equal to the distance between the center of borehole and the center of the pipe.

Note: The value of R_gg^1U may be negative as long as

1/R_gg^1U + 1/(2   R_gb^1U) > 0,

in which case the laws of thermodynamics are not violated. See Bauer et al. (2011) for details.

References

G. Hellström. Ground heat storage: thermal analyses of duct storage systems (Theory). Dept. of Mathematical Physics, University of Lund, Sweden, 1991.

D. Bauer, W. Heidemann, H. Müller-Steinhagen, and H.-J. G. Diersch. Thermal resistance and capacity models for borehole heat exchangers . International Journal Of Energy Research, 35:312–320, 2011.

Inputs

Outputs

Modelica definition

Buildings.Fluid.HeatExchangers.Boreholes.BaseClasses.temperatureDrop

Calculate the temperature drop of the soil at the external boundary of the cylinder

Information

This function calculates the temperature drop of the soil at the outer boundary of the cylinder. The analytical formula of Hart and Couvillion (1986) for constant heat extraction is adapted to a non-constant heat flux. To adapt the formula for a variable rate of heat extraction, different constant heat extraction rates, starting at different time instances, are super-imposed. To obtain the temperature drop at the time t=n*Δt, the effects of constant rate of heat extractions are super-imposed as

ΔT ( r , t=n Δt )= 1 ⁄ ( 4 π k ) ∑ W(u(r, t= i Δt)) (q_n-i+1-q_n-i),

where r is the radius for which the temperature is computed, k is the thermal conductivity of the material, W is a solution of the heat conduction in polar coordinates and q_i=Q_i/h is the specific rate of heat extraction per unit length at time t=i Δt. The value of W is obtained using

W(u)=[-0.5772 - ln(u) + u - u²/(2   2!) +u³/(3   3!) - u⁴/(4   4!) + ....].

where u(r,t)= c ρ r² ⁄ (4 t k) , ρ is the mass density and c is the specific heat capacity per unit mass.

Implementation

The rate of heat flow Q_i is obtained from the function Buildings.Fluid.HeatExchangers.Boreholes.BaseClasses.exchangeValues.

References

Hart and Couvillion, (1986). Earth Coupled Heat Transfer. Publication of the National Water Well Association.

Inputs

Outputs

Modelica definition