Buildings.Controls.OBC.Utilities.PIDWithAutotuning.AutoTuner.AMIGO
Package with components related to AMIGO tuners
Information
This package contains the blocks to implement an AMIGO (approximate M-constrained integral gain optimization) tuner. The AMIGO tuner calculates the parameters of PI/PID controllers based on the parameters of reduced order models. Those reduced order models approximate the control process.
References
Garpinger, Olof, Tore Hägglund, and Karl Johan Åström (2014) "Performance and robustness trade-offs in PID control." Journal of Process Control 24.5 (2014): 568-577.
Åström, Karl Johan and Tore Hägglund (2004) "Revisiting the Ziegler–Nichols step response method for PID control." Journal of Process Control 14.6 (2004): 635-650.
Package Content
| Name | Description |
|---|---|
 PI
|
Identify control gain and integral time of a PI controller |
 PID
|
Identify control gain, integral time, and derivative time of the PID model |
 Validation
|
Collection of models that validate the blocks in the AutoTuner |
 BaseClasses
|
Package with base classes |
Buildings.Controls.OBC.Utilities.PIDWithAutotuning.AutoTuner.AMIGO.PI
Identify control gain and integral time of a PI controller
Information
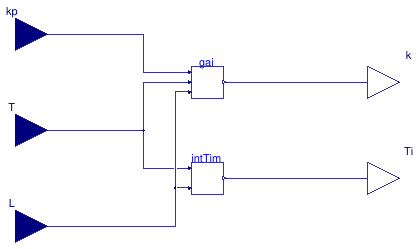
This block calculates the control gain and the integral time of a PI controller.
Refer to the following blocks for detailed information:
- Buildings.Controls.OBC.Utilities.PIDWithAutotuning.SystemIdentification.AutoTuner.BaseClasses.AMIGO.PIGain
- Buildings.Controls.OBC.Utilities.PIDWithAutotuning.SystemIdentification.AutoTuner.AMIGO.BaseClasses.PIIntegralTime
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | kp | Gain of a first-order plus time-delay (FOPTD) model |
| input RealInput | T | Time constant of the FOPTD model [s] |
| input RealInput | L | Time delay of the FOPTD model [s] |
| output RealOutput | k | Control gain signal |
| output RealOutput | Ti | Time constant signal for the integral term [s] |
Modelica definition
block PI "Identify control gain and integral time of a PI controller"
Buildings.Controls.OBC.CDL.Interfaces.RealInput kp(
final min=1E-6)
"Gain of a first-order plus time-delay (FOPTD) model";
Buildings.Controls.OBC.CDL.Interfaces.RealInput T(
final quantity="Time",
final unit="s",
final min=100*Buildings.Controls.OBC.CDL.Constants.eps)
"Time constant of the FOPTD model";
Buildings.Controls.OBC.CDL.Interfaces.RealInput L(
final quantity="Time",
final unit="s",
final min=100*Buildings.Controls.OBC.CDL.Constants.eps)
"Time delay of the FOPTD model";
Buildings.Controls.OBC.CDL.Interfaces.RealOutput k
"Control gain signal";
Buildings.Controls.OBC.CDL.Interfaces.RealOutput Ti(
final quantity="Time",
final unit="s",
final min=100*Buildings.Controls.OBC.CDL.Constants.eps)
"Time constant signal for the integral term";
protected
Buildings.Controls.OBC.Utilities.PIDWithAutotuning.AutoTuner.AMIGO.BaseClasses.PIGain
gai "Block that calculates the control gain";
Buildings.Controls.OBC.Utilities.PIDWithAutotuning.AutoTuner.AMIGO.BaseClasses.PIIntegralTime
intTim "Block that calculates the integral time";
equation
connect(gai.k, k);
connect(intTim.Ti, Ti);
connect(intTim.T, gai.T);
connect(intTim.L, gai.L);
connect(T, gai.T);
connect(L, gai.L);
connect(gai.kp, kp);
end PI;
Buildings.Controls.OBC.Utilities.PIDWithAutotuning.AutoTuner.AMIGO.PID
Identify control gain, integral time, and derivative time of the PID model
Information
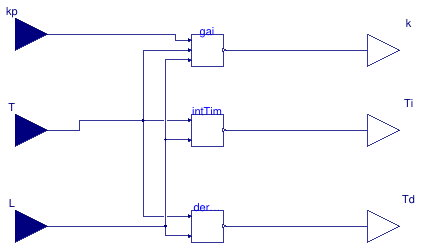
This block calculates the control gain, the integral time, and the derivative time of a PID model.
Refer to the following blocks for detailed information:
- Buildings.Controls.OBC.Utilities.PIDWithAutotuning.SystemIdentification.AutoTuner.AMIGO.BaseClasses.PIDGain
- Buildings.Controls.OBC.Utilities.PIDWithAutotuning.SystemIdentification.AutoTuner.AMIGO.BaseClasses.PIDIntegralTime
- Buildings.Controls.OBC.Utilities.PIDWithAutotuning.SystemIdentification.AutoTuner.AMIGO.BaseClasses.PIDDerivativeTime
Connectors
| Type | Name | Description |
|---|---|---|
| input RealInput | kp | Gain of a first-order plus time-delay (FOPTD) model |
| input RealInput | T | Time constant of the FOPTD model [s] |
| input RealInput | L | Time delay of the FOPTD model [s] |
| output RealOutput | k | Control gain signal |
| output RealOutput | Ti | Time constant signal for the integral term [s] |
| output RealOutput | Td | Time constant signal for the derivative term [s] |
Modelica definition
block PID "Identify control gain, integral time, and derivative time of the PID model"
Buildings.Controls.OBC.CDL.Interfaces.RealInput kp(
final min=1E-6)
"Gain of a first-order plus time-delay (FOPTD) model";
Buildings.Controls.OBC.CDL.Interfaces.RealInput T(
final quantity="Time",
final unit="s",
final min=100*Buildings.Controls.OBC.CDL.Constants.eps)
"Time constant of the FOPTD model";
Buildings.Controls.OBC.CDL.Interfaces.RealInput L(
final quantity="Time",
final unit="s",
final min=100*Buildings.Controls.OBC.CDL.Constants.eps)
"Time delay of the FOPTD model";
Buildings.Controls.OBC.CDL.Interfaces.RealOutput k
"Control gain signal";
Buildings.Controls.OBC.CDL.Interfaces.RealOutput Ti(
final quantity="Time",
final unit="s",
final min=100*Buildings.Controls.OBC.CDL.Constants.eps)
"Time constant signal for the integral term";
Buildings.Controls.OBC.CDL.Interfaces.RealOutput Td(
final quantity="Time",
final unit="s",
final min=100*Buildings.Controls.OBC.CDL.Constants.eps)
"Time constant signal for the derivative term";
protected
Buildings.Controls.OBC.Utilities.PIDWithAutotuning.AutoTuner.AMIGO.BaseClasses.PIDGain
gai "Block that calculates the control gain";
Buildings.Controls.OBC.Utilities.PIDWithAutotuning.AutoTuner.AMIGO.BaseClasses.PIDIntegralTime
intTim "Block that calculates the integral time";
Buildings.Controls.OBC.Utilities.PIDWithAutotuning.AutoTuner.AMIGO.BaseClasses.PIDDerivativeTime
derTim "Block that calculates the derivative time";
equation
connect(derTim.Td, Td);
connect(intTim.Ti, Ti);
connect(gai.k, k);
connect(intTim.T, gai.T);
connect(derTim.T, gai.T);
connect(intTim.L, gai.L);
connect(derTim.L, gai.L);
connect(kp, gai.kp);
connect(T, gai.T);
connect(L, gai.L);
end PID;