Buildings.Fluid.Geothermal.ZonedBorefields.BaseClasses.HeatTransfer
Package with ground heat transfer models
Information
This package contains models and functions to solve ground heat transfer around ground heat exchangers. For more information on the model implementation, see the documentation of Buildings.Fluid.Geothermal.ZonedBorefields.BaseClasses.HeatTransfer.GroundTemperatureResponse.
Extends from Modelica.Icons.VariantsPackage (Icon for package containing variants).
Package Content
| Name | Description |
|---|---|
| Model calculating discrete load aggregation | |
| Returns a SHA1 encryption of the formatted arguments for the thermal response factor generation | |
| Performs the shifting operation for load aggregation and determines the current cell | |
| Evaluate the thermal response factors of a zoned thermal storage | |
| Performs temporal superposition for the load aggregation procedure | |
| Validation models for the geothermal heat transfer models |
 Buildings.Fluid.Geothermal.ZonedBorefields.BaseClasses.HeatTransfer.GroundTemperatureResponse
Buildings.Fluid.Geothermal.ZonedBorefields.BaseClasses.HeatTransfer.GroundTemperatureResponse
Model calculating discrete load aggregation

Information
This model calculates the ground temperature response to obtain the temperature at the wall of each borehole segment in a geothermal system where heat is being injected into or extracted from the ground.
A load-aggregation scheme based on that developed by Claesson and Javed (2012)
is used to calculate the borehole wall temperature response with the temporal
and spatial superpositions of ground thermal loads. In its base form, the
load-aggregation scheme uses fixed-length aggregation cells to agglomerate
thermal load history together, with more distant cells (denoted with a higher
cell and vector index) representing more distant thermal history. The more
distant the thermal load, the less impactful it is on the borehole wall
temperature change at the current time step. Each cell has an
aggregation time associated to it denoted by nu,
which corresponds to the simulation time (since the beginning of heat injection
or extraction) at which the cell will begin shifting its thermal load to more
distant cells. To determine nu, cells have a temporal size
rcel (rcel in this model) which follows the
exponential growth :
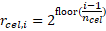
where nCel is the number of consecutive cells which can have the same size.
Decreasing rcel will generally decrease calculation times, at the cost of
precision in the temporal superposition. rcel is expressed in multiples
of the aggregation time resolution (via the parameter tLoaAgg).
Then, nu may be expressed as the sum of all rcel values
(multiplied by the aggregation time resolution) up to and including that cell in question.
The weighting factors giving the impact of the thermal load in a cell m) for a segment v of borehole J onto the temperature at the wall of segment u of a borehole I at the current time is obtained from analytical thermal response factors:
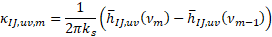
where hIJ,uv is the thermal response factor of segment
v of borehole J onto segment u of a
borehole I, ks is the thermal
conductivity of the soil and ν refers to the vector nu in
this model.
At every aggregation time step, a time event is generated to perform the load aggregation steps. First, the thermal loads are shifted. When shifting between cells of different size, total energy is conserved. This operation is illustred in the figure below by Cimmino (2014).
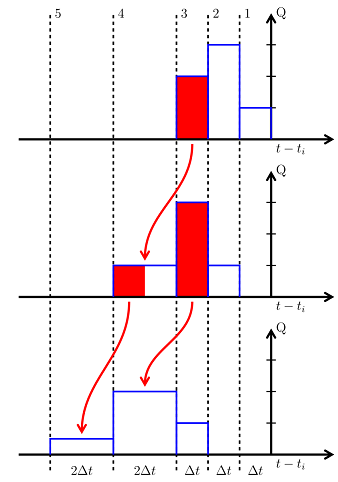
After the cell-shifting operation is performed, the first aggregation cell has its
value set to the average thermal load since the last aggregation step.
Temporal superposition is then applied by means
of a scalar product between the aggregated thermal loads QAgg_flow and the
weighting factors κ. The spatial superposition is applied by summing
the contributions of all segments on the total temperature variation.
Due to Modelica's variable time steps, the load aggregation scheme is modified by separating the thermal response between the current aggregation time step and everything preceding it. This is done according to :
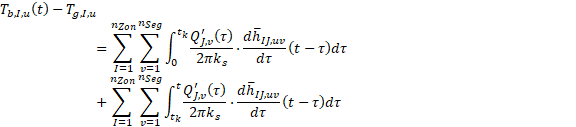
where Tb,I,u is the borehole wall temperature at segment
u of borehole I, Q'b,J,v is the ground thermal
load per borehole length at segment v of borehole J. tk
is the last discrete aggregation time step, meaning that the current time t
satisfies tk≤t≤tk+1.
Δtagg(=tk+1-tk) is the
parameter tLoaAgg in the present model.
Thermal interactions between segments affect the borehole wall temperature much slower than the effect of heat extraction at a segment on the temperature variation at the same segment. Thus, spatial superposition in the second sum can be neglected :
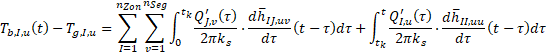
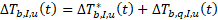
where ΔTb,I,u*(t) is the borehole wall temperature change at segment u of borehole I due to the thermal history prior to the current aggregation step. At every aggregation time step, spatial and temporal superpositions are used to calculate its discrete value. Assuming no heat injection or extraction until tk+1, this term is assumed to have a linear time derivative, which is given by the difference between ΔTb,I,u*(tk+1) (the temperature change from load history at the next discrete aggregation time step, which is constant over the duration of the ongoing aggregation time step) and the total temperature change at the last aggregation time step, ΔTb,I,u(tk).
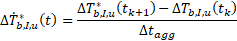
The second term ΔTb,q,I,u(t) concerns the ongoing aggregation time step.
To obtain the time derivative of this term, the thermal response factor hII,uu is assumed
to vary linearly over the course of an aggregation time step. Therefore, because
the ongoing aggregation time step always concerns the first aggregation cell, its
derivative can be calculated as kappa[i,i,1], the first value in the kappa array,
divided by the aggregation time step Δt.
The derivative of the temperature change at the borehole wall is then expressed
by its multiplication with the heat flow QI,u at
the borehole wall.
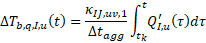
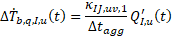
With the two terms in the expression of ΔTb,I,u(t) expressed
as time derivatives, ΔTb,I,u(t) can itself also be
expressed as its time derivative and implemented as such directly in the Modelica
equations block with the der() operator.
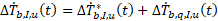
References
Cimmino, M. 2014. Développement et validation expérimentale de facteurs de réponse thermique pour champs de puits géothermiques, Ph.D. Thesis, École Polytechnique de Montréal.
Claesson, J. and Javed, S. 2012. A load-aggregation method to calculate extraction temperatures of borehole heat exchangers. ASHRAE Transactions 118(1): 530-539.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Time | tLoaAgg | 3600 | Time resolution of load aggregation [s] |
| Integer | nCel | 5 | Number of cells per aggregation level |
| Integer | nSeg | Number of segments per borehole | |
| Template | borFieDat | Record containing all the parameters of the borefield model |
Connectors
| Type | Name | Description |
|---|---|---|
| output RealOutput | delTBor[nZon, nSeg] | Temperature difference current borehole wall temperature minus initial borehole wall temperature [K] |
| input RealInput | QBor_flow[nZon, nSeg] | Heat flow from borehole segment (positive if heat from fluid into soil) [W] |
Modelica definition
 Buildings.Fluid.Geothermal.ZonedBorefields.BaseClasses.HeatTransfer.shaKappa
Buildings.Fluid.Geothermal.ZonedBorefields.BaseClasses.HeatTransfer.shaKappa
Returns a SHA1 encryption of the formatted arguments for the thermal response factor generation
Information
This function returns the SHA1 encryption of its arguments.
Implementation
Each argument is formatted in exponential notation
with four significant digits, for example 1.234e+001, with no spaces or
other separating characters between each argument value.
To prevent too long strings that can cause buffer overflows,
the sha encoding of each argument is computed and added to the next string that
is parsed.
The SHA1 encryption is computed using Buildings.Utilities.Cryptographics.sha.
Extends from Modelica.Icons.Function (Icon for functions).
Inputs
| Type | Name | Default | Description |
|---|---|---|---|
| Integer | nBor | Number of boreholes | |
| Position | cooBor[nBor, 2] | Coordinates of boreholes [m] | |
| Height | hBor | Borehole length [m] | |
| Height | dBor | Borehole buried depth [m] | |
| Radius | rBor | Borehole radius [m] | |
| ThermalDiffusivity | aSoi | Ground thermal diffusivity used in g-function evaluation [m2/s] | |
| ThermalConductivity | kSoi | Thermal conductivity of soil [W/(m.K)] | |
| Integer | nSeg | Number of line source segments per borehole | |
| Integer | nZon | Total number of independent bore field zones | |
| Integer | iZon[nBor] | Index of the zone corresponding to each borehole | |
| Integer | nBorPerZon[nZon] | Number of boreholes per borefield zone | |
| Time | nu[nTim] | Time vector for the calculation of thermal response factors [s] | |
| Integer | nTim | Length of the time vector | |
| Real | relTol | Relative tolerance on distance between boreholes |
Outputs
| Type | Name | Description |
|---|---|---|
| String | sha | SHA1 encryption of the g-function arguments |
Modelica definition
 Buildings.Fluid.Geothermal.ZonedBorefields.BaseClasses.HeatTransfer.shiftAggregationCells
Buildings.Fluid.Geothermal.ZonedBorefields.BaseClasses.HeatTransfer.shiftAggregationCells
Performs the shifting operation for load aggregation and determines the current cell
Information
Performs the shifting operation which propagates the thermal load history towards the more distant aggregation cells, and then sets the current cell's value at 0. Additionally, this function also outputs the last filled load aggregation cell.
This is a vectorized implementation of Buildings.Fluid.Geothermal.Borefields.BaseClasses.HeatTransfer.LoadAggregation.shiftAggregationCells, which applies load aggregation on a vector of aggregated load histories.
Extends from Modelica.Icons.Function (Icon for functions).
Inputs
| Type | Name | Default | Description |
|---|---|---|---|
| Integer | i | Number of aggregation cells | |
| Integer | nSeg | Number of segments | |
| HeatFlowRate | QAgg_flow[nSeg, i] | Vector of aggregated loads [W] | |
| Real | rCel[i] | Aggregation cell widths | |
| Time | nu[i] | Cell aggregation times [s] | |
| Time | curTim | Current simulation time [s] |
Outputs
| Type | Name | Description |
|---|---|---|
| Integer | curCel | Current occupied aggregation cell |
| HeatFlowRate | QAggShi_flow[nSeg, i] | Shifted vector of aggregated loads [W] |
Modelica definition
 Buildings.Fluid.Geothermal.ZonedBorefields.BaseClasses.HeatTransfer.temperatureResponseMatrix
Buildings.Fluid.Geothermal.ZonedBorefields.BaseClasses.HeatTransfer.temperatureResponseMatrix
Evaluate the thermal response factors of a zoned thermal storage
Information
This function evaluates the array of segment-to-segment thermal response factors using the analytical finite line source method of and Prieto and Cimmino (2021). The finite line source solution gives the relation between heat extraction at a segment of an equivalent borehole representing a group of boreholes (or in this model, a borefield zone) and the temperature variation at the wall of another segment of another (or the same) equivalent borehole representing another group of boreholes. The total temperature varition at a borehole segment is given by the temporal and spatial superpositions of the thermal reponse factors:
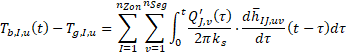
where Tb,I,u is the borehole wall temperature of segment u of borehole I, Tg,I,u is the undisturbed ground temperature of segment u of borehole I, Q'J,v is the heat injection rate into the ground through the borehole wall per unit length of segment v of borehole J, ks is the soil thermal conductivity and hIJ,uv is the thermal response factor of segment v of borehole J onto segment u of borehole I.
The thermal response factor is constructed from the combination of the finite
line source (FLS) solution (see
Buildings.Fluid.Geothermal.Borefields.BaseClasses.HeatTransfer.ThermalResponseFactors.finiteLineSource_Equivalent),
the cylindrical heat source (CHS) solution (see
Buildings.Fluid.Geothermal.Borefields.BaseClasses.HeatTransfer.ThermalResponseFactors.cylindricalHeatSource),
and the infinite line source (ILS) solution (see
Buildings.Fluid.Geothermal.Borefields.BaseClasses.HeatTransfer.ThermalResponseFactors.infiniteLineSource).
To obtain the thermal response factors of a bore field, the bore field is first
divided into nZon zones of parallel-connected boreholes. Each sone
is represented by a single equivalent borehole. Each equivalent borehole
is then divided into a series of nSeg segments of equal length,
each modeled as a line source of finite length. The finite line source solution
is superimposed in space to obtain a system of equations that gives the relation
between the heat injection rate at each of the segments and the borehole wall
temperature at each of the segments.
Since the finite line source solution is based on line sources of heat, rather than cylinders, the thermal response factors are corrected to consider the cylindrical geometry. The correction factor is then the difference between the cylindrical heat source solution and the infinite line source solution, as proposed by Li et al. (2014) :
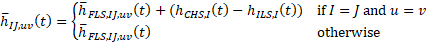
Implementation
The calculation of the g-function is separated into two regions: the
short-time region and the long-time region. In the short-time region,
corresponding to times t < 1 hour, heat interaction between boreholes
and axial variations of heat injection rate are not considered. The
g-function is calculated using only one borehole and one segment. In the
long-time region, corresponding to times t > 1 hour, all boreholes
are represented as series of nSeg line segments and the
g-function is evaluated as described above.
References
Li, M., Li, P., Chan, V. and Lai, A.C.K. 2014. Full-scale temperature response function (G-function) for heat transfer by borehole heat exchangers (GHEs) from sub-hour to decades. Applied Energy 136: 197-205.
Prieto, C. and Cimmino, M. 2021. Thermal interactions in large irregular fields of geothermal boreholes: the method of equivalent boreholes. Journal of Building Performance Simulation 14(4): 446-460. doi:10.1080/19401493.2021.1968953.
Extends from Modelica.Icons.Function (Icon for functions).
Inputs
| Type | Name | Default | Description |
|---|---|---|---|
| Integer | nBor | Number of boreholes | |
| Position | cooBor[nBor, 2] | Coordinates of boreholes [m] | |
| Height | hBor | Borehole length [m] | |
| Height | dBor | Borehole buried depth [m] | |
| Radius | rBor | Borehole radius [m] | |
| ThermalDiffusivity | aSoi | Ground thermal diffusivity used in g-function evaluation [m2/s] | |
| ThermalConductivity | kSoi | Thermal conductivity of soil [W/(m.K)] | |
| Integer | nSeg | Number of line source segments per borehole | |
| Integer | nZon | Total number of independent bore field zones | |
| Integer | iZon[nBor] | Index of the zone corresponding to each borehole | |
| Integer | nBorPerZon[nZon] | Number of boreholes per borefield zone | |
| Time | nu[nTim] | Time vector for the calculation of thermal response factors [s] | |
| Integer | nTim | Length of the time vector | |
| Real | relTol | 0.02 | Relative tolerance on distance between boreholes |
| String | sha | SHA-1 encryption of the arguments of this function |
Outputs
| Type | Name | Description |
|---|---|---|
| ThermalResistance | kappa[nZon*nSeg, nZon*nSeg, nTim] | Thermal response factor matrix [K/W] |
Modelica definition
 Buildings.Fluid.Geothermal.ZonedBorefields.BaseClasses.HeatTransfer.temporalSuperposition
Buildings.Fluid.Geothermal.ZonedBorefields.BaseClasses.HeatTransfer.temporalSuperposition
Performs temporal superposition for the load aggregation procedure
Information
Performs the temporal and spatial superposition operations to obtain the
temperature change at the wall of a borehole segment at the current time step.
The spatial superposition of one load aggregation cell is the matrix-vector
product of the kappa[:,:,k] step response matrix (at a cell k) and
the vector of aggregated loads of all borehole segments in cell k,
QAgg_flow[:,k]. The temporal superposition is the sum of the contributions of
all load aggregation cells. To avoid unnecessary calculations, the current
aggregation cell in the simulation is used to truncate the values from the
vectors that are not required.
This is a vectorized implementation of Buildings.Fluid.Geothermal.Borefields.BaseClasses.HeatTransfer.LoadAggregation.temporalSuperposition.
Extends from Modelica.Icons.Function (Icon for functions).
Inputs
| Type | Name | Default | Description |
|---|---|---|---|
| Integer | i | Number of aggregation cells | |
| Integer | nSeg | Number of segments | |
| HeatFlowRate | QAgg_flow[nSeg, i] | Array of aggregated loads [W] | |
| ThermalResistance | kappa[nSeg, nSeg, i] | Weighting factors for each aggregation cell [K/W] | |
| Integer | curCel | Current occupied aggregation cell |
Outputs
| Type | Name | Description |
|---|---|---|
| TemperatureDifference | deltaTb[nSeg] | Delta T at wall [K] |
