Buildings.Fluid.Storage.Ice
Ice tank model
Information
Package with ice thermal storage models.
Extends from Modelica.Icons.Package (Icon for standard packages).
Package Content
| Name | Description |
|---|---|
| Ice tank with performance based on performance curves and built-in control for outlet temperature | |
| Ice tank with performance based on performance curves | |
| Performance data for ice thermal tank | |
| Package that validates the ice tank model | |
| Base classes for ice tank models |
 Buildings.Fluid.Storage.Ice.ControlledTank
Buildings.Fluid.Storage.Ice.ControlledTank
Ice tank with performance based on performance curves and built-in control for outlet temperature
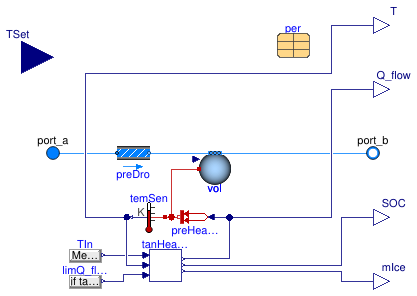
Information
This model implements an ice tank model with built-in idealized control
that tracks the set point TSet for the temperature of the working fluid
that leaves the tank, as shown in the figure below.
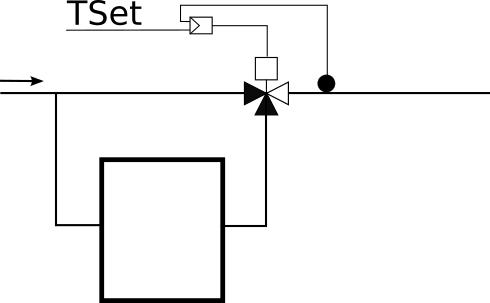
The model is identical to Buildings.Fluid.Storage.Ice.Tank, except that it takes as an input the set point for the temperature of the leaving working fluid. This temperature is maintained if the flow rate and temperatures allow sufficient heat flow rate between the tank and the working fluid.
The built-in control is an idealization of a tank that has a controller that
bypasses some of the working fluid in order to meet the set point for the temperature
of the leaving working fluid.
The fluid from port_a to port_b has by default
a first order response. If the tank has sufficient capacity for the given
inlet temperature and flow rate, then the idealized control has no
steady-state error. During transients, the set point may not be met
exactly due to the first order response that approximates the dynamics
of the heat exchanger.
Note that the setpoint is also tracked during charging mode.
If the full flow rate should go through the tank during charging,
which is generally desired, then set TSet to a
high temperature, such as 20°C.
Usage
This model requires the fluid to flow from port_a to port_b.
Otherwise, the simulation stops with an error.
Extends from Buildings.Fluid.Storage.Ice.Tank (Ice tank with performance based on performance curves).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| replaceable package Medium | PartialMedium | Medium in the component | |
| Generic | per | redeclare parameter Building... | Performance data |
| Nominal condition | |||
| MassFlowRate | m_flow_nominal | Nominal mass flow rate [kg/s] | |
| PressureDifference | dp_nominal | Pressure difference [Pa] | |
| Advanced | |||
| MassFlowRate | m_flow_small | 1E-4*abs(m_flow_nominal) | Small mass flow rate for regularization of zero flow [kg/s] |
| Diagnostics | |||
| Boolean | show_T | false | = true, if actual temperature at port is computed |
| Flow resistance | |||
| Boolean | from_dp | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | linearizeFlowResistance | false | = true, use linear relation between m_flow and dp for any flow rate |
| Real | deltaM | 0.1 | Fraction of nominal flow rate where flow transitions to laminar |
| Initialization | |||
| AbsolutePressure | p_start | Medium.p_default | Start value of pressure [Pa] |
| Temperature | T_start | Medium.T_default | Start value of temperature [K] |
| MassFraction | X_start[Medium.nX] | Medium.X_default | Start value of mass fractions m_i/m [kg/kg] |
| ExtraProperty | C_start[Medium.nC] | fill(0, Medium.nC) | Start value of trace substances |
| Real | SOC_start | Start value for state of charge [1] | |
| Dynamics heat exchanger | |||
| Conservation equations | |||
| Dynamics | energyDynamicsHex | Modelica.Fluid.Types.Dynamic... | Formulation of energy balance for heat exchanger internal fluid mass |
| Time | tauHex | 30 | Time constant of working fluid through the heat exchanger at nominal flow [s] |
Connectors
| Type | Name | Description |
|---|---|---|
| FluidPort_a | port_a | Fluid connector a (positive design flow direction is from port_a to port_b) |
| FluidPort_b | port_b | Fluid connector b (positive design flow direction is from port_a to port_b) |
| output RealOutput | SOC | state of charge [1] |
| output RealOutput | T | Temperature of the fluid leaving at port_b [K] |
| output RealOutput | mIce | Mass of remaining ice [kg] |
| output RealOutput | Q_flow | Heat flow rate, positive during charging, negative when melting the ice [W] |
| input RealInput | TSet | Outlet temperature setpoint during discharging [K] |
Modelica definition
 Buildings.Fluid.Storage.Ice.Tank
Buildings.Fluid.Storage.Ice.Tank
Ice tank with performance based on performance curves
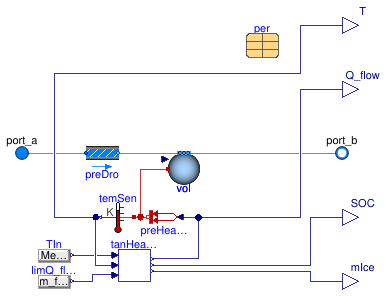
Information
This model implements an ice tank model whose performance is computed based on performance curves.
The model is based on the implementation of Guowen et al., 2020 and similar to the detailed EnergyPlus ice tank model ThermalStorage:Ice:Detailed.
The governing equations are as follows:
The mass of ice in the storage mice is calculated as
d SOC/dt = Q̇/(Hf mice,max)
mice = SOC mice,max
where SOC is state of charge, Q̇ is the heat transfer rate of the ice tank, positive for charging and negative for discharging, Hf is the fusion of heat of ice and mice,max is the nominal mass of ice in the storage tank.
The heat transfer rate of the ice tank Q̇ is computed using
Q̇ = Qsto,nom q*,
where Qsto,nom is the storage capacity and q* is a normalized heat flow rate. The storage capacity is
Qsto,nom = Hf mice,max,
where Hf is the latent heat of fusion of ice and mice,max is the maximum ice storage capacity.
The normalized heat flow rate is computed using performance curves for charging (freezing) or discharging (melting). For charging, the heat transfer rate q* between the chilled water and the ice in the thermal storage tank is calculated using
q* Δt = C1 + C2x + C3 x2 + [C4 + C5x + C6 x2]ΔTlmtd*
where Δt is the time step of the data samples used for the curve fitting, C1-6 are the curve fit coefficients, x is the fraction of charging, also known as the state-of-charge, and Tlmtd* is the normalized LMTD calculated using Buildings.Fluid.Storage.Ice.BaseClasses.calculateLMTDStar. Similarly, for discharging, the heat transfer rate q* between the chilled water and the ice in the thermal storage tank is
- q* Δt = D1 + D2(1-x) + D3 (1-x)2 + [D4 + D5(1-x) + D6 (1-x)2]ΔTlmtd*
where Δt is the time step of the data samples used for the curve fitting, D1-6 are the curve fit coefficients.
The normalized LMTD ΔTlmtd* uses a nominal temperature difference of 10 Kelvin. This value must be used when obtaining the curve fit coefficients.
The log mean temperature difference is calculated using
ΔTlmtd* = ΔTlmtd/Tnom
ΔTlmtd = (Tin - Tout)/ln((Tin - Tfre)/(Tout - Tfre))
where Tin is the inlet temperature, Tout is the outlet temperature, Tfre is the freezing temperature and Tnom is a nominal temperature difference of 10 Kelvin.
Usage
This model requires the fluid to flow from port_a to port_b.
Otherwise, the simulation stops with an error.
Reference
Strand, R.K. 1992. “Indirect Ice Storage System Simulation,” M.S. Thesis, Department of Mechanical and Industrial Engineering, University of Illinois at Urbana-Champaign.
Guowen Li, Yangyang Fu, Amanda Pertzborn, Jin Wen and Zheng O'Neill. An Ice Storage Tank Modelica Model: Implementation and Validation. Modelica Conferences. 2021. doi:10.3384/ecp21181177.
Extends from Buildings.Fluid.Interfaces.TwoPortHeatMassExchanger (Partial model transporting one fluid stream with storing mass or energy).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| replaceable package Medium | PartialMedium | Medium in the component | |
| Generic | per | redeclare parameter Building... | Performance data |
| Nominal condition | |||
| MassFlowRate | m_flow_nominal | Nominal mass flow rate [kg/s] | |
| PressureDifference | dp_nominal | Pressure difference [Pa] | |
| Assumptions | |||
| Boolean | allowFlowReversal | false | = false to simplify equations, assuming, but not enforcing, no flow reversal |
| Advanced | |||
| MassFlowRate | m_flow_small | 1E-4*abs(m_flow_nominal) | Small mass flow rate for regularization of zero flow [kg/s] |
| Diagnostics | |||
| Boolean | show_T | false | = true, if actual temperature at port is computed |
| Flow resistance | |||
| Boolean | from_dp | false | = true, use m_flow = f(dp) else dp = f(m_flow) |
| Boolean | linearizeFlowResistance | false | = true, use linear relation between m_flow and dp for any flow rate |
| Real | deltaM | 0.1 | Fraction of nominal flow rate where flow transitions to laminar |
| Dynamics | |||
| Nominal condition | |||
| Time | tau | tauHex | Time constant at nominal flow (if energyDynamics <> SteadyState) [s] |
| Conservation equations | |||
| Dynamics | energyDynamics | energyDynamicsHex | Type of energy balance: dynamic (3 initialization options) or steady state |
| Initialization | |||
| AbsolutePressure | p_start | Medium.p_default | Start value of pressure [Pa] |
| Temperature | T_start | Medium.T_default | Start value of temperature [K] |
| MassFraction | X_start[Medium.nX] | Medium.X_default | Start value of mass fractions m_i/m [kg/kg] |
| ExtraProperty | C_start[Medium.nC] | fill(0, Medium.nC) | Start value of trace substances |
| Real | SOC_start | Start value for state of charge [1] | |
| Dynamics heat exchanger | |||
| Conservation equations | |||
| Dynamics | energyDynamicsHex | Modelica.Fluid.Types.Dynamic... | Formulation of energy balance for heat exchanger internal fluid mass |
| Time | tauHex | 30 | Time constant of working fluid through the heat exchanger at nominal flow [s] |
Connectors
| Type | Name | Description |
|---|---|---|
| FluidPort_a | port_a | Fluid connector a (positive design flow direction is from port_a to port_b) |
| FluidPort_b | port_b | Fluid connector b (positive design flow direction is from port_a to port_b) |
| output RealOutput | SOC | state of charge [1] |
| output RealOutput | T | Temperature of the fluid leaving at port_b [K] |
| output RealOutput | mIce | Mass of remaining ice [kg] |
| output RealOutput | Q_flow | Heat flow rate, positive during charging, negative when melting the ice [W] |
