Buildings.Fluid.Movers.BaseClasses.Euler
Functions and data record templates for Euler number
Information
This package implements a power computation using the Euler number and its correlation.
- The correlation function using the Euler number is implemented in Buildings.Fluid.Movers.BaseClasses.Euler.correlation.
- When curves of power and pressure against flow rate is available, the function Buildings.Fluid.Movers.BaseClasses.Euler.getPeak can identify the peak operating condition from them. This is useful comparing power computation results against other methods.
- The peak operating condition (where the efficiency η is at its maximum) which is used by the correlation is stored in an instance of the record Buildings.Fluid.Movers.BaseClasses.Euler.peak.
- Buildings.Fluid.Movers.BaseClasses.FlowMachineInterface uses the peak values and the correlation to generate a power curve against volumetric flow rate. This estimated power curve is used in place of the measured power that would otherwise be provided.
See the User's Guide for more information.
Package Content
| Name | Description |
|---|---|
| Correlation of static efficiency ratio vs log of Euler number ratio | |
| Computes efficiency with the Euler number correlation | |
| Find peak condition from power characteristics | |
| Computes power as well as its derivative with respect to flow rate using Euler number | |
| Record for the operation condition at peak efficiency | |
| Record for electrical power and its derivative with respect to flow rate |
 Buildings.Fluid.Movers.BaseClasses.Euler.correlation
Buildings.Fluid.Movers.BaseClasses.Euler.correlation
Correlation of static efficiency ratio vs log of Euler number ratio
Information
This function approximates the following correlation:

where y=η ⁄ ηp (note that η refers to the hydraulic efficiency instead of total efficiency), x=log10(Eu ⁄ Eup), with the subscript p denoting the condition where the mover is operating at peak efficiency, and
Z1=(x-a) ⁄ b
Z2=(ec⋅x⋅d⋅x-a) ⁄ b
Z3=-a ⁄ b
a=-2.732094
b=2.273014
c=0.196344
d=5.267518
The approximation uses two simple polynomials stitched together by
a third one of the same order.
Care has been taken to ensure that, on the curve constructed by
if statements, the differences of dy ⁄ dx
evaluated by different groups of coefficients at the connecting points
(i.e. at x = - 0.5 and x = + 0.5) are less than 1E-14.
This way, the derivative is still continuous to the solver even if
the solver requires a precision of 1E-10 when there are nested loops.
The correlation and the approximation have the shape as shown below (plotted by Buildings.Fluid.Movers.BaseClasses.Validation.EulerCurve).
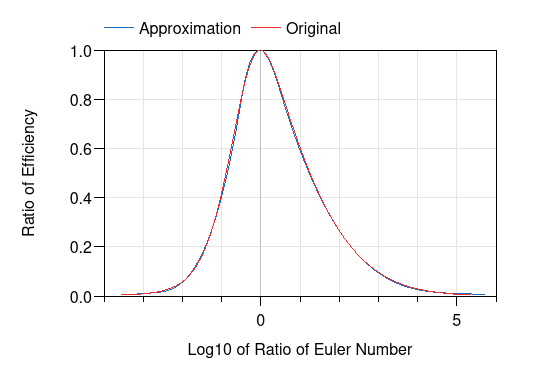
The modified dimensionless Euler number is defined as
Eu=(Δp⋅D4) ⁄ (ρ⋅V̇2)
where Δp is the fan pressure rise in Pa, D is the fan wheel outer diameter in m, ρ is the inlet air density in kg/m3, and V̇ is the volumetric flow rate in m3/s. Note that the units in the definition do not matter to this correlation because it is the ratio of the Euler numbers that is used. Since D is constant for the same mover and ρ is approximately constant for common HVAC applications, the Euler number ratio can be simplified to
Eu ⁄ Eup=(Δp⋅V̇p2) ⁄ (Δpp⋅V̇2)
References
For more information regarding the correlation curve refer to EnergyPlus 9.6.0 Engineering Reference chapter 16.4 equations 16.209 through 16.218. Note that the formula is simplified here from the source document.
Resources
The svg file for the correlation equation was generated on https://viereck.ch/latex-to-svg using this script.
Extends from Modelica.Icons.Function (Icon for functions).
Inputs
| Type | Name | Default | Description |
|---|---|---|---|
| Real | x | log10(Eu/Eu_peak) |
Outputs
| Type | Name | Description |
|---|---|---|
| Real | y | eta/eta_peak |
Modelica definition
 Buildings.Fluid.Movers.BaseClasses.Euler.efficiency
Buildings.Fluid.Movers.BaseClasses.Euler.efficiency
Computes efficiency with the Euler number correlation
Information
This function uses the correlation of Euler number to compute the efficiency η.
Extends from Modelica.Icons.Function (Icon for functions).
Inputs
| Type | Name | Default | Description |
|---|---|---|---|
| peak | peak | Operation point with maximum efficiency | |
| PressureDifference | dp | Pressure rise [Pa] | |
| VolumeFlowRate | V_flow | Volumetric flow rate [m3/s] | |
| Real | V_flow_dp_small | Small number for regularisation [m3.Pa/s] |
Outputs
| Type | Name | Description |
|---|---|---|
| Efficiency | eta | Efficiency [1] |
Modelica definition
 Buildings.Fluid.Movers.BaseClasses.Euler.getPeak
Buildings.Fluid.Movers.BaseClasses.Euler.getPeak
Find peak condition from power characteristics
Information
This function finds or estimates the peak point (V̇,Δp,η)|η=ηmax from the input power curve P(V̇) and pressure curve Δp(V̇) which may or may not contain non-zero values. The results are output as an instance of Buildings.Fluid.Movers.BaseClasses.Euler.peak. There are the following branches of computation based on information provided to the function:
- If Δp(V̇) is unavailable, the function simply outputs (0,0,0.7).
- If Δp(V̇) is provided but P(V̇) is unavailable, the function provides an estimation of the peak point at half of max flow rate (V̇max ⁄ 2, Δp(V̇=V̇max ⁄ 2), 0.7).
-
If both Δp(V̇) and P(V̇) are available,
the function first computes
η(V̇)=V̇ Δp ⁄ P.
-
If η(V̇) has less than four data points or is monotonic,
use one of the two which ever produces a higher η:
- The interpolated point at half of max flow rate (V̇max ⁄ 2, Δp(V̇=V̇max ⁄ 2), η(V̇=V̇max ⁄ 2))
- The available point with the highest computed efficiency.
- Otherwise, the function runs a quartic regression on η(V̇) then solves its derivative to find an extremum. It assumes that there is only one extremum on the open interval (0,V̇max).
-
If η(V̇) has less than four data points or is monotonic,
use one of the two which ever produces a higher η:
Extends from Modelica.Icons.Function (Icon for functions).
Inputs
| Type | Name | Default | Description |
|---|---|---|---|
| flowParameters | pressure | Pressure vs. flow rate | |
| powerParameters | power | Power vs. flow rate |
Outputs
| Type | Name | Description |
|---|---|---|
| peak | peak | Operation point at maximum efficiency |
Modelica definition
 Buildings.Fluid.Movers.BaseClasses.Euler.power
Buildings.Fluid.Movers.BaseClasses.Euler.power
Computes power as well as its derivative with respect to flow rate using Euler number
Information
This function outputs power values as well as its derivative versus volumetric flow rate in the following steps:
- It first interpolates the input pressure curve to find a new pressure curve of 11 points on 10% increments of max flow rate. It assumes that the last point on the input pressure curve corresponds to Δp = 0, which is ensured when this function is called by Buildings.Fluid.Movers.BaseClasses.FlowMachineInterface.
- It then computes power using efficiency evaluated with the Euler number from 10% to 90% of max flow rate on 10% increments.
- With the incomplete power curve it computes the spline derivatives with respect to flow rate at the same points.
- Once the derivatives are available, the power values at the two boundary points are found through linear extrapolation.
These steps are designed to ensure that power and efficiency computation with
the Euler number is handled correctly near zero flow or zero pressure, where
Ẇflo = 0,
η = 0,
P > 0
in the equation
η = Ẇflo ⁄ P.
Extends from Modelica.Icons.Function (Icon for functions).
Inputs
| Type | Name | Default | Description |
|---|---|---|---|
| peak | peak | Peak operation point | |
| flowParametersInternal | pressure | Pressure curve with both max flow rate and max pressure |
Outputs
| Type | Name | Description |
|---|---|---|
| powerWithDerivative | power | Power and its derivative vs. flow rate |
Modelica definition
 Buildings.Fluid.Movers.BaseClasses.Euler.peak
Buildings.Fluid.Movers.BaseClasses.Euler.peak
Record for the operation condition at peak efficiency
Information
Record for performance data that describe the operation at peak efficiency.
Extends from Modelica.Icons.Record (Icon for records).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| VolumeFlowRate | V_flow | Volume flow rate at peak efficiency [m3/s] | |
| PressureDifference | dp | Pressure rise at peak efficiency [Pa] | |
| Efficiency | eta | 0.7 | Peak efficiency [1] |
Modelica definition
 Buildings.Fluid.Movers.BaseClasses.Euler.powerWithDerivative
Buildings.Fluid.Movers.BaseClasses.Euler.powerWithDerivative
Record for electrical power and its derivative with respect to flow rate
Information
Data record for performance data that describe electrical power and its derivative versus volumetric flow rate. This record is specifically constructed for the Euler number method and is the output type of function Buildings.Fluid.Movers.BaseClasses.Euler.power.
Extends from Modelica.Icons.Record (Icon for records).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| VolumeFlowRate | V_flow[11] | Volume flow rate at user-selected operating points [m3/s] | |
| Power | P[11] | Fan or pump electrical power at these flow rates [W] | |
| Real | d[11] | Derivative of power with respect to volume flow rate [J/m3] |
