Buildings.Fluid.HydronicConfigurations.Examples
Example models
Information
This package contains generic examples illustrating the concept of valve authority.
Extends from Modelica.Icons.ExamplesPackage (Icon for packages containing runnable examples).
Package Content
| Name | Description |
|---|---|
| Model illustrating the concept of the authority for two-way valves and open loop control |
 Buildings.Fluid.HydronicConfigurations.Examples.TwoWayOpenLoop
Buildings.Fluid.HydronicConfigurations.Examples.TwoWayOpenLoop
Model illustrating the concept of the authority for two-way valves and open loop control
Information
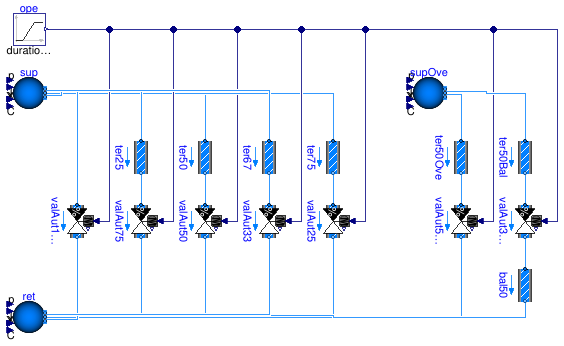
This model illustrates the concept of the authority for two-way valves controlled with an open loop that modulates the valve from fully closed to fully open position. The valve authority β = Δp(y=100%) / Δp(y=0%) can be computed by dividing the pressure drop across the valve between those two extreme positions (see plot #2 for the pressure drop values and the command log for the computed value of the authority).
-
The components
valAut<25..100>show how the authority affects the inherent flow characteristic of the valve which corresponds to an authority β = 100% (see plot #1). The major disturbance appears for authorities strictly lower than β = 50% which is usually adopted as the sizing criteria for control valves. -
The components
valAut50OveandvalAut33Balillustrate the concept of "practical authority". The circuits are exposed to a pressure differential 50% higher than design whereas the valve size is identical in both cases (Kvs = 5.1 m3/h/bar^(1/2)). The circuit withvalAut33Balincludes a balancing valve that enables reaching the design flow when the control valve is fully open. The computed authority forvalAut50Ove(β = 50%) is higher than forvalAut33Bal(β = 33%) due to the overflow in fully open conditions for the former component. This is paradoxical because practically the controllability should be similar in a real system since the two valves are identical and the pressure differential at the circuit boundaries is the same. To support that statement one can notice that the rate of change of the flow rate with respect to the valve opening is similar between the two components at low valve opening (y ≤ 50% ). Now computing the practical authority we get: β' = β / (V̇actual / V̇design)2 = 33% for those two components. This yields the following statements.- The practical authority does not vary whether the circuit is balanced or not, as opposed to the conventional authority.
- The practical authority only depends on the valve size and the available pressure differential at the circuit boundaries.
-
The conventional authority does not depend on the available pressure
differential at the circuit boundaries as it affects Δpmin
and / Δpmax with the same factor (see for instance
components
valAut50andvalAut50Ove). - The disturbance of the flow characteristic of the valve (flow rate normalized by its maximum value, as a function of the valve opening, see plot #3) is explained by the conventional authority. However, this has little value if the maximum flow rate is significantly different from the design value. Normalizing by the design flow rate gives more indication on the controllability of the system. The disturbance of the flow characteristic (when the fractional flow rate is expressed as a fraction of the design flow rate, see plot #1) is then explained by the practical authority as d(V̇(y) / V̇design) / dy = 1 / β' 1/2 * d(Kv(y) / Kvs) / dy when y tends towards zero and where the function Kv(y) / Kvs is the inherent valve characteristic.
Extends from Modelica.Icons.Example (Icon for runnable examples).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| MassFlowRate | mLiq_flow_nominal | 1 | Circuit mass flow rate at design conditions [kg/s] |
| Pressure | p_min | 2E5 | Circuit minimum pressure [Pa] |
| PressureDifference | dp_nominal | 1E5 | Circuit total pressure drop at design conditions [Pa] |
