Buildings.Utilities.Math.Examples

Information

Package Content

Name	Description
RegNonZeroPower
RegNonZeroPowerDerivative_2_Check
RegNonZeroPowerDerivativeCheck
SmoothBlocks
SmoothExponentialDerivativeCheck
SpliceFunction
SpliceFunctionDerivativeCheck

Buildings.Utilities.Math.Examples.RegNonZeroPower

Modelica definition

model RegNonZeroPower 
  Real y "Function value";
equation 
  y=Buildings.Utilities.Math.regNonZeroPower(time, 0.3, 0.5);
end RegNonZeroPower;

Buildings.Utilities.Math.Examples.RegNonZeroPowerDerivative_2_Check

Information

This example checks whether the function derivative is implemented correctly. If the derivative implementation is not correct, the model will stop with an assert statement.

Parameters

Type	Name	Default	Description
Real	n	0.33	Exponent
Real	delta	0.1	Abscissa value where transition occurs

Modelica definition

model RegNonZeroPowerDerivative_2_Check 
  
 parameter Real n=0.33 "Exponent";
 parameter Real delta = 0.1 "Abscissa value where transition occurs";
  
  Real x;
  Real y;
initial equation 
   y=x;
equation 
  x=Buildings.Utilities.Math.BaseClasses.der_regNonZeroPower(time,n, delta, time);
  der(y)=der(x);
  assert(abs(x-y) < 1E-2, "Model has an error");
  
end RegNonZeroPowerDerivative_2_Check;

Buildings.Utilities.Math.Examples.RegNonZeroPowerDerivativeCheck

Information

This example checks whether the function derivative is implemented correctly. If the derivative implementation is not correct, the model will stop with an assert statement.

Parameters

Type	Name	Default	Description
Real	n	0.33	Exponent
Real	delta	0.1	Abscissa value where transition occurs

Modelica definition

model RegNonZeroPowerDerivativeCheck 
  
 parameter Real n=0.33 "Exponent";
 parameter Real delta = 0.1 "Abscissa value where transition occurs";
  
  Real x;
  Real y;
initial equation 
   y=x;
equation 
  x=Buildings.Utilities.Math.regNonZeroPower(time,n, delta);
  der(y)=der(x);
  assert(abs(x-y) < 1E-2, "Model has an error");
  
end RegNonZeroPowerDerivativeCheck;

Buildings.Utilities.Math.Examples.SmoothBlocks

Modelica definition

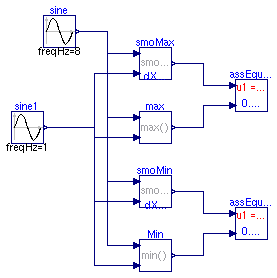
model SmoothBlocks 
  SmoothMax smoMax(deltaX=0.5);
  Modelica.Blocks.Math.Max max;
  Modelica.Blocks.Sources.Sine sine(freqHz=8);
  Modelica.Blocks.Sources.Sine sine1;
  Controls.AssertEquality assEquMax(threShold=0.08);
  SmoothMin smoMin(deltaX=0.5);
  Modelica.Blocks.Math.Min Min;
  Controls.AssertEquality assEquMin(threShold=0.08);
equation 
  
  connect(sine.y, smoMax.u1);
  connect(sine.y, max.u1);
  connect(sine1.y, smoMax.u2);
  connect(sine1.y, max.u2);
  connect(smoMax.y, assEquMax.u1);
  connect(max.y, assEquMax.u2);
  connect(sine.y, smoMin.u1);
  connect(sine.y, Min.u1);
  connect(sine1.y, smoMin.u2);
  connect(sine1.y, Min.u2);
  connect(smoMin.y, assEquMin.u1);
  connect(Min.y, assEquMin.u2);
end SmoothBlocks;

Buildings.Utilities.Math.Examples.SmoothExponentialDerivativeCheck

Information

This example checks whether the function derivative is implemented correctly. If the derivative implementation is not correct, the model will stop with an assert statement.

Modelica definition

model SmoothExponentialDerivativeCheck 
  
  
  Real x;
  Real y;
  Real ex "exact function value";
initial equation 
   y=x;
equation 
  x=Buildings.Utilities.Math.smoothExponential(x=time-2, delta=0.5);
  der(y)=der(x);
  assert(abs(x-y) < 1E-2, "Model has an error");
  ex=exp(-abs(time-2));
end SmoothExponentialDerivativeCheck;

Buildings.Utilities.Math.Examples.SpliceFunction

Modelica definition

model SpliceFunction 
  Real y "Function value";
equation 
  y=Buildings.Utilities.Math.spliceFunction(10, -10, time+0.1, 0.2);
end SpliceFunction;

Buildings.Utilities.Math.Examples.SpliceFunctionDerivativeCheck

Information

This example checks whether the function derivative is implemented correctly. If the derivative implementation is not correct, the model will stop with an assert statement.

Modelica definition

model SpliceFunctionDerivativeCheck 
  
  Real x;
  Real y;
initial equation 
   y=x;
equation 
  x=Buildings.Utilities.Math.spliceFunction(10, -10, time+0.1, 0.2);
  der(y)=der(x);
  assert(abs(x-y) < 1E-2, "Model has an error");
  
end SpliceFunctionDerivativeCheck;