Buildings.Fluids.Actuators.BaseClasses

Package Content

Name	Description
der_equalPercentage	Derivative of valve opening characteristics for equal percentage valve
der_exponentialDamper	Derivative of damper opening characteristics for an exponential damper
equalPercentage	Valve opening characteristics for equal percentage valve
Examples	Collection of models that illustrate model use and test models
exponentialDamper	Damper opening characteristics for an exponential damper
PartialActuator	Partial model of an actuator
PartialDamperExponential	Partial model for air dampers with exponential opening characteristics
PartialThreeWayValve	Partial three way valve
PartialTwoWayValve	Partial model for a two way valve

Buildings.Fluids.Actuators.BaseClasses.der_equalPercentage

Information

This function computes the derivative of the opening characteristics of an equal percentage valve.

The function is the derivative of TwoWayValveEqualPercentage.

Inputs

Type	Name	Default	Description
Real	y		Valve opening signal, y=1 is fully open
Real	R		Rangeability, R=50...100 typically
Real	l		Valve leakage, l=Cv(y=0)/Cvs
Real	delta		Range of significant deviation from equal percentage law
Real	der_y		Derivative of valve opening signal

Outputs

Type	Name	Description
Real	der_phi	Derivative of ratio actual to nominal mass flow rate, dphi/dy

Modelica definition

function der_equalPercentage 
  "Derivative of valve opening characteristics for equal percentage valve" 
  
  input Real y "Valve opening signal, y=1 is fully open";
  input Real R "Rangeability, R=50...100 typically";
  input Real l(min=0, max=1) "Valve leakage, l=Cv(y=0)/Cvs";
  input Real delta "Range of significant deviation from equal percentage law";
  input Real der_y "Derivative of valve opening signal";
  
  output Real der_phi 
    "Derivative of ratio actual to nominal mass flow rate, dphi/dy";
protected 
   Real a "Polynomial coefficient";
   Real b "Polynomial coefficient";
   Real c "Polynomial coefficient";
   Real logR "=log(R)";
   Real z "Auxiliary variable";
   Real q "Auxiliary variable";
   Real p "Auxiliary variable";
algorithm 
  if y < delta/2 then
    der_phi := (R^(delta-1) - l) / delta;
  else
    if (y > (3/2 * delta)) then
      der_phi := R^(y-1)*ln(R);
    else
      logR := Modelica.Math.log(R);
      z := (3*delta/2);
      q := delta*R^z*logR;
      p := R^z;
      a := (q - 2*p + 2*R^delta)/(delta^3*R);
      b := (-5*q + 12*p - 13*R^delta + l*R)/(2*delta^2*R);
      c := (7*q - 18*p + 24*R^delta - 6*l*R)/(4*delta*R);
      der_phi  := c + y * ( 2*b + 3*a*y);
    end if;
  end if;
end der_equalPercentage;

Buildings.Fluids.Actuators.BaseClasses.der_exponentialDamper

Information

This function computes the derivative of the opening characteristics of an exponential damper.

The function is used by the model Dampers.Exponential.

For yL < y < yU, the damper characteristics is

  k = exp(a+b*(1-y)).

Inputs

Type	Name	Default	Description
Real	y		Control signal, y=0 is closed, y=1 is open
Real	a		Coefficient a for damper characteristics
Real	b		Coefficient b for damper characteristics
Real	cL[3]		Polynomial coefficients for curve fit for y < yl
Real	cU[3]		Polynomial coefficients for curve fit for y > yu
Real	yL		Lower value for damper curve
Real	yU		Upper value for damper curve
Real	der_y		Derivative of control signal

Outputs

Type	Name	Description
Real	der_kTheta	Derivative of flow coefficient, der_kTheta=dkTheta/dy

Modelica definition

function der_exponentialDamper 
  "Derivative of damper opening characteristics for an exponential damper" 
  
  input Real y(unit="") "Control signal, y=0 is closed, y=1 is open";
  input Real a(unit="") "Coefficient a for damper characteristics";
  input Real b(unit="") "Coefficient b for damper characteristics";
  input Real[3] cL "Polynomial coefficients for curve fit for y < yl";
  input Real[3] cU "Polynomial coefficients for curve fit for y > yu";
  input Real yL "Lower value for damper curve";
  input Real yU "Upper value for damper curve";
  input Real der_y(unit="") "Derivative of control signal";
  
  output Real der_kTheta(min=0) 
    "Derivative of flow coefficient, der_kTheta=dkTheta/dy";
algorithm 
  if y < yL then
    der_kTheta := exp(cL[3] + y * (cL[2] + y * cL[1]))*(2 * cL[1] * y + cL[2]);
  else
    if (y > yU) then
      der_kTheta := exp(cU[3] + y * (cU[2] + y * cU[1]))*(2 * cU[1] * y + cU[2]);
    else
      der_kTheta := -b*exp(a+b*(1-y)) 
        "y=0 is closed, but theta=1 is closed in ASHRAE-825";
    end if;
  end if;
end der_exponentialDamper;

Buildings.Fluids.Actuators.BaseClasses.equalPercentage

Information

This function computes the opening characteristics of an equal percentage valve.

The function is used by the model TwoWayValveEqualPercentage.

For y < delta/2, the valve characteristics is linear. For y > 3*delta/2 the valve characteristics is equal percentage. In between, a cubic spline is used to ensure that the valve characteristics is once continuously differentiable with respect to y.

Inputs

Type	Name	Default	Description
Real	y		Valve opening signal, y=1 is fully open
Real	R		Rangeability, R=50...100 typically
Real	l		Valve leakage, l=Cv(y=0)/Cvs
Real	delta		Range of significant deviation from equal percentage law

Outputs

Type	Name	Description
Real	phi	Ratio actual to nominal mass flow rate, phi=Cv(y)/Cv(y=1)

Modelica definition

function equalPercentage 
  "Valve opening characteristics for equal percentage valve" 
  annotation(derivative=der_equalPercentage);  
  
  input Real y "Valve opening signal, y=1 is fully open";
  input Real R "Rangeability, R=50...100 typically";
  input Real l(min=0, max=1) "Valve leakage, l=Cv(y=0)/Cvs";
  input Real delta "Range of significant deviation from equal percentage law";
  output Real phi "Ratio actual to nominal mass flow rate, phi=Cv(y)/Cv(y=1)";
protected 
   Real a "Polynomial coefficient";
   Real b "Polynomial coefficient";
   Real c "Polynomial coefficient";
   Real d "Polynomial coefficient";
   Real logR "=log(R)";
   Real z "Auxiliary variable";
   Real q "Auxiliary variable";
   Real p "Auxiliary variable";
algorithm 
  if y < delta/2 then
    phi := l + y * (R^(delta-1) - l) / delta;
  else
    if (y > (3/2 * delta)) then
      phi := R^(y-1);
    else
      logR := Modelica.Math.log(R);
      z := (3*delta/2);
      q := delta*R^z*logR;
      p := R^z;
      a := (q - 2*p + 2*R^delta)/(delta^3*R);
      b := (-5*q + 12*p - 13*R^delta + l*R)/(2*delta^2*R);
      c := (7*q - 18*p + 24*R^delta - 6*l*R)/(4*delta*R);
      d := (-3*q + 8*p - 9*R^delta + 9*l*R)/(8*R);
      phi  := d + y * ( c + y * ( b + y * a));
    end if;
  end if;
end equalPercentage;

Buildings.Fluids.Actuators.BaseClasses.exponentialDamper

Information

This function computes the opening characteristics of an exponential damper.

The function is used by the model Dampers.Exponential.

For yL < y < yU, the damper characteristics is

  k = exp(a+b*(1-y)).

Inputs

Type	Name	Default	Description
Real	y		Control signal, y=0 is closed, y=1 is open
Real	a		Coefficient a for damper characteristics
Real	b		Coefficient b for damper characteristics
Real	cL[3]		Polynomial coefficients for curve fit for y < yl
Real	cU[3]		Polynomial coefficients for curve fit for y > yu
Real	yL		Lower value for damper curve
Real	yU		Upper value for damper curve

Outputs

Type	Name	Description
Real	kTheta	Flow coefficient, kTheta = pressure drop divided by dynamic pressure

Modelica definition

function exponentialDamper 
  "Damper opening characteristics for an exponential damper" 
  annotation(derivative=der_exponentialDamper);  
  
  input Real y(unit="") "Control signal, y=0 is closed, y=1 is open";
  input Real a(unit="") "Coefficient a for damper characteristics";
  input Real b(unit="") "Coefficient b for damper characteristics";
  input Real[3] cL "Polynomial coefficients for curve fit for y < yl";
  input Real[3] cU "Polynomial coefficients for curve fit for y > yu";
  input Real yL "Lower value for damper curve";
  input Real yU "Upper value for damper curve";
  
  output Real kTheta(min=0) 
    "Flow coefficient, kTheta = pressure drop divided by dynamic pressure";
algorithm 
  if y < yL then
    kTheta := exp(cL[3] + y * (cL[2] + y * cL[1]));
  else
    if (y > yU) then
      kTheta := exp(cU[3] + y * (cU[2] + y * cU[1]));
    else
      kTheta := exp(a+b*(1-y)) "y=0 is closed";
    end if;
  end if;
end exponentialDamper;

Buildings.Fluids.Actuators.BaseClasses.PartialActuator

Information

Parameters

Type	Name	Default	Description
replaceable package Medium		PartialMedium	Medium in the component
MassFlowRate	m_small_flow		Mass flow rate where transition to laminar occurs [kg/s]
Initialization
MassFlowRate	m_flow		Mass flow rate from port_a to port_b (m_flow > 0 is design flow direction) [kg/s]
Pressure	dp		Pressure difference between port_a and port_b [Pa]
Advanced
Temp	flowDirection	Modelica_Fluid.Types.FlowDir...	Unidirectional (port_a -> port_b) or bidirectional flow component
Boolean	from_dp	true	= true, use m_flow = f(dp) else dp = f(m_flow)
Boolean	linearized	false	= true, use linear relation between m_flow and dp for any flow rate

Connectors

Type	Name	Description
FluidPort_a	port_a	Fluid connector a (positive design flow direction is from port_a to port_b)
FluidPort_b	port_b	Fluid connector b (positive design flow direction is from port_a to port_b)
input RealInput	y	Damper position (0: closed, 1: open)

Modelica definition

partial model PartialActuator "Partial model of an actuator" 
  extends Buildings.Fluids.BaseClasses.PartialResistance;
  import SI = Modelica.SIunits;
  
  
public 
  Modelica.Blocks.Interfaces.RealInput y(min=0, max=1) 
    "Damper position (0: closed, 1: open)";
end PartialActuator;

Buildings.Fluids.Actuators.BaseClasses.PartialDamperExponential

Information

Partial model for air dampers with exponential opening characteristics. This is the base model for air dampers. The model defines the flow rate where the linearization near the origin occurs. The model also defines parameters that are used by different air damper models.

This model does not assign k=kDam because the model VAVBoxExponential consists of a fixed resistance and a resistance due to the air damper. If k would be assigned here, then this partial model could not be used as a base class for VAVBoxExponential.

For a description of the opening characteristics and typical parameter values, see the damper model Exponential.

Parameters

Type	Name	Default	Description
replaceable package Medium		PartialMedium	Medium in the component
MassFlowRate	m_small_flow	eta0*ReC*sqrt(A)*facRouDuc	Mass flow rate where transition to laminar occurs [kg/s]
Area	A		Face area [m2]
Boolean	roundDuct	false	Set to true for round duct, false for square cross section
Real	ReC	4000	Reynolds number where transition to laminar starts
Real	a	-1.51	Coefficient a for damper characteristics
Real	b	0.105*90	Coefficient b for damper characteristics
Real	yL	15/90	Lower value for damper curve
Real	yU	55/90	Upper value for damper curve
Real	k0	1E6	Flow coefficient for y=0, k0 = pressure drop divided by dynamic pressure
Real	k1	0.45	Flow coefficient for y=1, k1 = pressure drop divided by dynamic pressure
Initialization
MassFlowRate	m_flow		Mass flow rate from port_a to port_b (m_flow > 0 is design flow direction) [kg/s]
Pressure	dp		Pressure difference between port_a and port_b [Pa]
Advanced
Temp	flowDirection	Modelica_Fluid.Types.FlowDir...	Unidirectional (port_a -> port_b) or bidirectional flow component
Boolean	from_dp	true	= true, use m_flow = f(dp) else dp = f(m_flow)
Boolean	linearized	false	= true, use linear relation between m_flow and dp for any flow rate

Connectors

Type	Name	Description
FluidPort_a	port_a	Fluid connector a (positive design flow direction is from port_a to port_b)
FluidPort_b	port_b	Fluid connector b (positive design flow direction is from port_a to port_b)
input RealInput	y	Damper position (0: closed, 1: open)

Modelica definition

partial model PartialDamperExponential 
  "Partial model for air dampers with exponential opening characteristics" 
  extends PartialActuator(m_small_flow=eta0*ReC*sqrt(A)*facRouDuc);
  
  parameter Modelica.SIunits.Area A "Face area";
  parameter Boolean roundDuct = false 
    "Set to true for round duct, false for square cross section";
  parameter Real ReC=4000 "Reynolds number where transition to laminar starts";
  
  parameter Real a(unit="")=-1.51 "Coefficient a for damper characteristics";
  parameter Real b(unit="")=0.105*90 "Coefficient b for damper characteristics";
  parameter Real yL = 15/90 "Lower value for damper curve";
  parameter Real yU = 55/90 "Upper value for damper curve";
  parameter Real k0(min=0) = 1E6 
    "Flow coefficient for y=0, k0 = pressure drop divided by dynamic pressure";
  parameter Real k1(min=0) = 0.45 
    "Flow coefficient for y=1, k1 = pressure drop divided by dynamic pressure";
  Real kDam(unit="(kg*m)^(1/2)", start=1) 
    "Flow coefficient for damper, k=m_flow/sqrt(dp)";
  
protected 
  Real kTheta(min=0) 
    "Flow coefficient, kTheta = pressure drop divided by dynamic pressure";
  parameter Real[3] cL(fixed=false) 
    "Polynomial coefficients for curve fit for y < yl";
  parameter Real[3] cU(fixed=false) 
    "Polynomial coefficients for curve fit for y > yu";
  
protected 
  parameter Real facRouDuc= if roundDuct then sqrt(Modelica.Constants.pi)/2 else 1;
initial equation 
 cL[1] = (ln(k0) - b - a)/yL^2;
 cL[2] = (-b*yL - 2*ln(k0) + 2*b + 2*a)/yL;
 cL[3] = ln(k0);
  
 cU[1] = (ln(k1) - a)/(yU^2 - 2*yU + 1);
 cU[2] = (-b*yU^2 - 2*ln(k1)*yU - (-2*b - 2*a)*yU - b)/(yU^2 - 2*yU + 1);
 cU[3] = (ln(k1)*yU^2 + b*yU^2 + (-2*b - 2*a)*yU + b + a)/(yU^2 - 2*yU + 1);
 assert(k0 > k1, "k0 must be bigger than k1.");
equation 
   kTheta = exponentialDamper(y=y, a=a, b=b, cL=cL, cU=cU, yL=yL, yU=yU) 
    "y=0 is closed";
   assert(kTheta>=0, "Flow coefficient must not be negative");
   kDam = sqrt(2*medium_a.d/kTheta) * A 
    "flow coefficient for resistance base model, kDam=k=m_flow/sqrt(dp)";
  
end PartialDamperExponential;

Buildings.Fluids.Actuators.BaseClasses.PartialThreeWayValve

Information

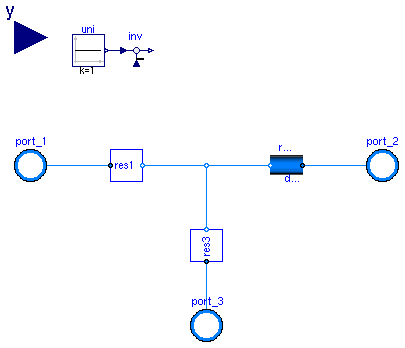
Partial model of a three way valve. This is the base model for valves with different opening characteristics, such as linear, equal percentage or quick opening. The three way valve model consists of a mixer where valves are placed in two of the flow legs. The third flow leg has no friction. The flow coefficient k_SI for flow from port_1 -> port_2 is a parameter and the flow coefficient for flow from port_3 -> port_2 is computed as

         k_SI(port_1 -> port_2)
  fraK = ----------------------
         k_SI(port_3 -> port_2)

Since this model uses two way valves to construct a three way valve, see PartialTwoWayValve for details regarding the valve implementation.

Parameters

Type	Name	Default	Description
replaceable package Medium		PartialMedium	Fluid medium model
PartialTwoPortTransport	res1	redeclare Modelica_Fluid.Int...	Partial model, to be replaced with a fluid component
PartialTwoPortTransport	res3	redeclare Modelica_Fluid.Int...	Partial model, to be replaced with a fluid component
Real	k_SI		Flow coefficient for fully open valve in SI units, k=m_flow/sqrt(dp) [(kg*m)^(1/2)]
Real	fraK	0.7	Fraction k_SI(port_1->port_2)/k_SI(port_3->port_2)
Real	l[2]	{0,0}	Valve leakage, l=Cv(y=0)/Cvs
Pressure-flow linearization
Real	deltaM	0.02	Fraction of nominal flow rate where linearization starts, if y=1
Pressure	dp0	6000	Nominal pressure drop [Pa]
Advanced
Boolean	from_dp	true	= true, use m_flow = f(dp) else dp = f(m_flow)
Temp	flowDirection	Modelica_Fluid.Types.FlowDir...	Unidirectional (port_1 -> port_2) or bidirectional flow component
Boolean	linearized[2]	{false,false}	= true, use linear relation between m_flow and dp for any flow rate

Connectors

Type	Name	Description
FluidPort_b	port_1
FluidPort_b	port_2
input RealInput	y	Damper position (0: closed, 1: open)

Modelica definition

partial model PartialThreeWayValve "Partial three way valve" 
    extends Buildings.Fluids.BaseClasses.PartialThreeWayResistance(
        port_3(
        m_flow(start=0,min=if allowFlowReversal then -Modelica.Constants.inf else 0)),
      redeclare FixedResistances.LosslessPipe res2(
          redeclare package Medium = Medium,
          flowDirection=Modelica_Fluid.Types.FlowDirection.Bidirectional));
  
  
  parameter Real k_SI(min=0, unit="(kg*m)^(1/2)") 
    "Flow coefficient for fully open valve in SI units, k=m_flow/sqrt(dp)";
  parameter Real fraK(min=0, max=1) = 0.7 
    "Fraction k_SI(port_1->port_2)/k_SI(port_3->port_2)";
  parameter Real[2] l(min=0, max=1) = {0, 0} "Valve leakage, l=Cv(y=0)/Cvs";
  parameter Real deltaM = 0.02 
    "Fraction of nominal flow rate where linearization starts, if y=1";
  parameter Modelica.SIunits.Pressure dp0 = 6000 "Nominal pressure drop";
  parameter Boolean[2] linearized = {false, false} 
    "= true, use linear relation between m_flow and dp for any flow rate";
  
  Modelica.Blocks.Interfaces.RealInput y "Damper position (0: closed, 1: open)";
protected 
  Modelica.Blocks.Math.Feedback inv "Inversion of control signal";
  Modelica.Blocks.Sources.Constant uni(final k=1) 
    "Outputs one for bypass valve";
equation 
  connect(uni.y, inv.u1);
end PartialThreeWayValve;

Buildings.Fluids.Actuators.BaseClasses.PartialTwoWayValve

Information

Partial model for a two way valve. This is the base model for valves with different opening characteristics, such as linear, equal percentage or quick opening.

The parameter k_SI is the flow coefficient in SI units, i.e., it is the ratio between mass flow rate in kg/s and square root of pressure drop in Pa.

To prevent the derivative d/dP (m_flow) to assume infinity near the origin, this model linearizes the pressure drop vs. flow relation ship. The region in which it is linearized is parameterized by

m_small_flow = deltaM * k_SI * sqrt(dp0)

The two way valve models are implemented using this partial model, as opposed to using different functions for the valve opening characteristics, because each valve opening characteristics has different parameters.

Parameters

Type	Name	Default	Description
replaceable package Medium		PartialMedium	Medium in the component
Real	k_SI		Flow coefficient for fully open valve in SI units, k=m_flow/sqrt(dp) [(kg*m)^(1/2)]
Real	l	0.005	Valve leakage, l=Cv(y=0)/Cvs
Initialization
MassFlowRate	m_flow		Mass flow rate from port_a to port_b (m_flow > 0 is design flow direction) [kg/s]
Pressure	dp		Pressure difference between port_a and port_b [Pa]
Pressure-flow linearization
Real	deltaM	0.02	Fraction of nominal flow rate where linearization starts, if y=1
Pressure	dp0	6000	Nominal pressure drop [Pa]
Advanced
Temp	flowDirection	Modelica_Fluid.Types.FlowDir...	Unidirectional (port_a -> port_b) or bidirectional flow component
Boolean	from_dp	true	= true, use m_flow = f(dp) else dp = f(m_flow)
Boolean	linearized	false	= true, use linear relation between m_flow and dp for any flow rate

Connectors

Type	Name	Description
FluidPort_a	port_a	Fluid connector a (positive design flow direction is from port_a to port_b)
FluidPort_b	port_b	Fluid connector b (positive design flow direction is from port_a to port_b)
input RealInput	y	Damper position (0: closed, 1: open)

Modelica definition

partial model PartialTwoWayValve "Partial model for a two way valve" 
  extends PartialActuator(final m_small_flow = deltaM * k_SI * sqrt(dp0));
  
  parameter Real k_SI(min=0, unit="(kg*m)^(1/2)") 
    "Flow coefficient for fully open valve in SI units, k=m_flow/sqrt(dp)";
  parameter Real l(min=0, max=1) = 0.005 "Valve leakage, l=Cv(y=0)/Cvs";
  parameter Real deltaM = 0.02 
    "Fraction of nominal flow rate where linearization starts, if y=1";
  parameter Modelica.SIunits.Pressure dp0 = 6000 "Nominal pressure drop";
  Real phi "Ratio actual to nominal mass flow rate, phi=Cv(y)/Cv(y=1)";
equation 
 k = phi * k_SI;
end PartialTwoWayValve;