Modelica.Magnetic.FundamentalWave.Components

Information

Basic components of the FundamentalWave library for modeling magnetic circuits. Machine specific components are located at Machines.Components.

Extends from Modelica.Icons.Package (Icon for standard packages).

Package Content

Name	Description
Ground	Magnetic ground
Reluctance	Salient reluctance
EddyCurrent	Constant loss model under sinusoidal magnetic conditions
SinglePhaseElectroMagneticConverter	Single phase electro magnetic converter
MultiPhaseElectroMagneticConverter	Multi phase electro magnetic converter
Idle	Salient reluctance
Short	Salient reluctance

Modelica.Magnetic.FundamentalWave.Components.Ground

Information

Grounding of the complex magnetic potential. Each magnetic circuit has to be grounded at least one point of the circuit.

Connectors

Type	Name	Description
PositiveMagneticPort	port_p	Complex magnetic port

Modelica definition

model Ground "Magnetic ground"

  Interfaces.PositiveMagneticPort port_p "Complex magnetic port";

equation 
  port_p.V_m = Complex(0,0);
end Ground;

Modelica.Magnetic.FundamentalWave.Components.Reluctance

Information

The salient reluctance models the relationship between the complex magnetic potential difference 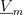and the complex magnetic flux ,

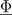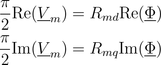
which can also be expressed in terms complex phasors:

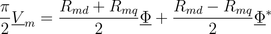
Extends from Modelica.Magnetic.FundamentalWave.Interfaces.PartialTwoPortElementary (Two magnetic ports for textual modeling).

Parameters

Type	Name	Default	Description
SalientReluctance	R_m		Magnetic reluctance in d=re and q=im axis

Connectors

Type	Name	Description
PositiveMagneticPort	port_p	Positive complex magnetic port
NegativeMagneticPort	port_n	Negative complex magnetic port

Modelica definition

model Reluctance "Salient reluctance"

  import Modelica.Constants.pi;

  extends Modelica.Magnetic.FundamentalWave.Interfaces.PartialTwoPortElementary;
  parameter Modelica.Magnetic.FundamentalWave.Types.SalientReluctance R_m(
    d(start=1), q(start=1)) "Magnetic reluctance in d=re and q=im axis";

equation 
  (pi/2) * V_m.re = R_m.d * Phi.re;
  (pi/2) * V_m.im = R_m.q * Phi.im;
end Reluctance;

Modelica.Magnetic.FundamentalWave.Components.EddyCurrent

Information

The eddy current loss model with respect to fundamental wave effects is designed in accordance to FluxTubes.Basic.EddyCurrent.

  .

Fig. 1: equivalent models of eddy current losses

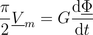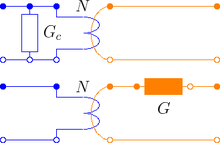
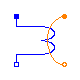
Due to the nature of eddy current losses, which can be represented by symmetric conductors in an equivalent electric circuit (Fig. 1), the respective number of phases 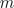has to be taken into account. Assume that the 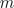conductances of the equivalent circuit are 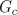, the conductance for the eddy current loss model is determined by

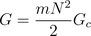
where 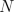is the number of turns of the symmetric electro magnetic coupling.

For such an 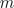phase system the relationship between the voltage and current space phasors and the magnetic flux and magnetic potential difference phasor is

  ,
  ,

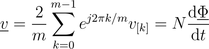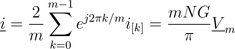where 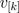and 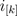are the phase voltages and currents, respectively.

The dissipated loss power

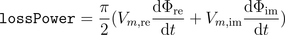
can be determined for the space phasor relationship of the voltage and current space phasor.

See also

FluxTubes.Basic.EddyCurrent

Extends from Modelica.Magnetic.FundamentalWave.Interfaces.PartialTwoPortElementary (Two magnetic ports for textual modeling), Modelica.Thermal.HeatTransfer.Interfaces.PartialElementaryConditionalHeatPort (Partial model to include a conditional HeatPort in order to dissipate losses, used for textual modeling, i.e., for elementary models).

Parameters

Type	Name	Default	Description
Conductance	G		Eqivalent symmetric loss conductance [S]
Boolean	useHeatPort	false	=true, if heatPort is enabled
Temperature	T	273.15	Fixed device temperature if useHeatPort = false [K]

Connectors

Type	Name	Description
PositiveMagneticPort	port_p	Positive complex magnetic port
NegativeMagneticPort	port_n	Negative complex magnetic port
HeatPort_a	heatPort	Optional port to which dissipated losses are transported in form of heat

Modelica definition

model EddyCurrent 
  "Constant loss model under sinusoidal magnetic conditions"

  import Modelica.Constants.pi;

  extends Modelica.Magnetic.FundamentalWave.Interfaces.PartialTwoPortElementary;
  parameter Modelica.SIunits.Conductance G(min=0) 
    "Eqivalent symmetric loss conductance";
  extends Modelica.Thermal.HeatTransfer.Interfaces.PartialElementaryConditionalHeatPort
    (final T = 273.15);

equation 
  lossPower = (pi/2)*(V_m.re*der(Phi.re) + V_m.im*der(Phi.im));
  if G>0 then
    (pi/2) * V_m.re = G * der(Phi.re);
    (pi/2) * V_m.im = G * der(Phi.im);
  else
    V_m.re = 0;
    V_m.im = 0;
  end if;
end EddyCurrent;

Modelica.Magnetic.FundamentalWave.Components.SinglePhaseElectroMagneticConverter

Information

The single phase winding has an effective number of turns, 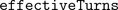and a respective orientation of the winding, 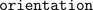. The current in winding is .

The total complex magnetic potential difference of the single phase winding is determined by:

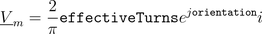
In this equation the magneto motive force is aligned with the orientation of the winding.

The voltage induced in the winding depends on the cosine between the orientation of the winding and the angle of the complex magnetic flux. Additionally, the magnitudes of the induced voltages are propotional to the respective number of turns. This relationship can be modeled by means of

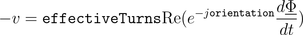
The single phase electro magnetic converter is a special case of the MultiPhaseElectroMagneticConverter

See also

MultiPhaseElectroMagneticConverter

Parameters

Type	Name	Default	Description
Real	effectiveTurns		Effective number of turns
Angle	orientation		Orientation of the resulting fundamental wave V_m phasor [rad]

Connectors

Type	Name	Description
PositivePin	pin_p	Positive pin
NegativePin	pin_n	Negative pin
PositiveMagneticPort	port_p	Positive complex magnetic port
NegativeMagneticPort	port_n	Negative complex magnetic port

Modelica definition

model SinglePhaseElectroMagneticConverter 
  "Single phase electro magnetic converter"

  import Modelica.Constants.pi;

  Modelica.Electrical.Analog.Interfaces.PositivePin pin_p "Positive pin";
  Modelica.Electrical.Analog.Interfaces.NegativePin pin_n "Negative pin";

  Interfaces.PositiveMagneticPort port_p "Positive complex magnetic port";
  Interfaces.NegativeMagneticPort port_n "Negative complex magnetic port";

  parameter Real effectiveTurns "Effective number of turns";
  parameter Modelica.SIunits.Angle orientation 
    "Orientation of the resulting fundamental wave V_m phasor";

  // Local electric single phase quantities
  Modelica.SIunits.Voltage v "Voltage drop";
  Modelica.SIunits.Current i "Current";

  // Local electromagnetic fundamental wave quantities
  Modelica.SIunits.ComplexMagneticPotentialDifference  V_m 
    "Complex magnetic potential difference";
  Modelica.SIunits.ComplexMagneticFlux  Phi "Complex magnetic flux";

  final parameter Complex N=
    effectiveTurns * Modelica.ComplexMath.exp(Complex(0,orientation)) 
    "Complex number of turns";

equation 
  // Magnetic flux and flux balance of the magnetic ports
  port_p.Phi = Phi;
  port_p.Phi + port_n.Phi = Complex(0,0);

  // Magnetic potential difference of the magnetic ports
  port_p.V_m - port_n.V_m = V_m;

  // Voltage drop between the electrical pins
  v = pin_p.v - pin_n.v;

  // Current and current balance of the electric pins
  i = pin_p.i;
  pin_p.i + pin_n.i = 0;

  // Complex magnetic potential difference is determined from currents, number
  // of turns and angles of orientation of winding
  // V_m.re = (2/pi) * effectiveTurns*cos(orientation)*i;
  // V_m.im = (2/pi) * effectiveTurns*sin(orientation)*i;
  V_m = (2.0/pi) * N * i;

  // Induced voltages is determined from complex magnetic flux, number of turns
  // and angles of orientation of winding
  // -v = effectiveTurns*cos(orientation)*der(Phi.re)
  //    + effectiveTurns*sin(orientation)*der(Phi.im);
  -v = Modelica.ComplexMath.real(Modelica.ComplexMath.conj(N)*Complex(der(Phi.re),der(Phi.im)));

end SinglePhaseElectroMagneticConverter;

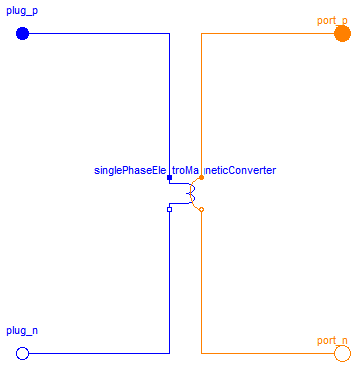
Modelica.Magnetic.FundamentalWave.Components.MultiPhaseElectroMagneticConverter

Information

Each phase 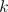of an 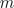phase winding has an effective number of turns, 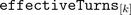and an respective winging angle 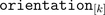and a phase current .

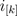The total complex magnetic potential difference of the mutli phase winding is determined by:

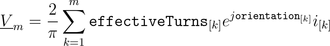
In this equation each contribution of a winding magneto motive force on the total complex magnetic potential difference is aligned with the respective orientation of the winding.

The voltages 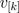induced in each winding depend on the cosinus between the orientation of the winding and the angle of the complex magnetic flux. Additionally, the magnitudes of the induced voltages are propotional to the respective number of turns. This relationship can be modeled by means of

for 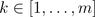and is also illustrated by the following figure:

Fig: Orientation of winding and location of complex magnetic flux

See also

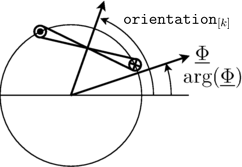
SinglePhaseElectroMagneticConverter

Parameters

Type	Name	Default	Description
Integer	m	3	Number of phases
Real	effectiveTurns[m]		Effective number of turns
Angle	orientation[m]		Orientation of the resulting fundamental wave field phasor [rad]

Connectors

Type	Name	Description
PositivePlug	plug_p	Positive plug
NegativePlug	plug_n	Negative plug
PositiveMagneticPort	port_p	Positive complex magnetic port
NegativeMagneticPort	port_n	Negative complex magnetic port

Modelica definition

model MultiPhaseElectroMagneticConverter 
  "Multi phase electro magnetic converter"

  import Modelica.Constants.pi;

  Modelica.Electrical.MultiPhase.Interfaces.PositivePlug plug_p(
    final m=m) "Positive plug";
  Modelica.Electrical.MultiPhase.Interfaces.NegativePlug plug_n(
    final m=m) "Negative plug";

  Modelica.Magnetic.FundamentalWave.Interfaces.PositiveMagneticPort port_p 
    "Positive complex magnetic port";
  Modelica.Magnetic.FundamentalWave.Interfaces.NegativeMagneticPort port_n 
    "Negative complex magnetic port";

  parameter Integer m = 3 "Number of phases";
  parameter Real effectiveTurns[m] "Effective number of turns";
  parameter Modelica.SIunits.Angle orientation[m] 
    "Orientation of the resulting fundamental wave field phasor";

  Modelica.Magnetic.FundamentalWave.Components.SinglePhaseElectroMagneticConverter
    singlePhaseElectroMagneticConverter[m](
      final effectiveTurns=effectiveTurns,
      final orientation=orientation);
equation 
  connect(plug_p.pin, singlePhaseElectroMagneticConverter.pin_p);
  connect(singlePhaseElectroMagneticConverter.pin_n, plug_n.pin);
  connect(singlePhaseElectroMagneticConverter[1].port_p, port_p);
  for k in 2:m loop
    connect(singlePhaseElectroMagneticConverter[k-1].port_n,singlePhaseElectroMagneticConverter[k].port_p);
  end for;
  connect(singlePhaseElectroMagneticConverter[m].port_n, port_n);

end MultiPhaseElectroMagneticConverter;

Modelica.Magnetic.FundamentalWave.Components.Idle

Information

This is a simple idle running branch.

See also

Short

Extends from Modelica.Magnetic.FundamentalWave.Interfaces.PartialTwoPortElementary (Two magnetic ports for textual modeling).

Connectors

Type	Name	Description
PositiveMagneticPort	port_p	Positive complex magnetic port
NegativeMagneticPort	port_n	Negative complex magnetic port

Modelica definition

model Idle "Salient reluctance"
  extends Modelica.Magnetic.FundamentalWave.Interfaces.PartialTwoPortElementary;
equation 
  Phi = Complex(0,0);
end Idle;

Modelica.Magnetic.FundamentalWave.Components.Short

Information

This is a simple short cut branch.

See also

Idle

Extends from Modelica.Magnetic.FundamentalWave.Interfaces.PartialTwoPort (Two magnetic ports for graphical modeling).

Connectors

Type	Name	Description
PositiveMagneticPort	port_p	Positive complex magnetic port
NegativeMagneticPort	port_n	Negative complex magnetic port

Modelica definition

model Short "Salient reluctance"
  extends Modelica.Magnetic.FundamentalWave.Interfaces.PartialTwoPort;

equation 
  connect(port_p, port_n);
end Short;