Modelica.Magnetic.FundamentalWave.BasicMachines.Functions

Information

This package contains auxiliary functions for electric machine models.

Extends from Modelica.Icons.Package (Icon for standard packages).

Package Content

Name	Description
symmetricOrientation	Orientations of the resulting fundamental wave field phasors

Modelica.Magnetic.FundamentalWave.BasicMachines.Functions.symmetricOrientation

Information

This function determines the orientation of the symmetrical winding with 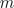phases. For an odd number of phases the difference of the windings angles of two adjacent phases is 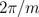. In case of an even number of phases the aligned orientation of winding is not modeled since they do not add any information. Instead the 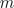windings are divided into two different groups. The first group refers to the indices . The second group covers the indices 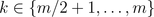. The difference of the windings angles of two adjacent phases - of both the first and the second group, respectively - is 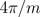. The phase shift of the two groups .

Inputs

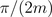Type	Name	Default	Description
Integer	m		Number of phases

Outputs

Type	Name	Description
Angle	orientation[m]	Orientation of the resulting fundamental wave field phasors [rad]

Modelica definition

function symmetricOrientation 
  "Orientations of the resulting fundamental wave field phasors"

  import Modelica.Constants.pi;

  input Integer m "Number of phases";
  output Modelica.SIunits.Angle orientation[m] 
    "Orientation of the resulting fundamental wave field phasors";

algorithm 
  if mod(m,2) == 0 then
    // Even number of phases
    for k in 1:integer(m/2) loop
      orientation[k] :=(k - 1)*4*pi/m;
      orientation[k+integer(m/2)] := orientation[k] + 2*pi/m;
    end for;
  else
    // Odd number of phases
    orientation :={(k - 1)*2*pi/m for k in 1:m};
  end if;
end symmetricOrientation;