Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.PressureLoss.General

Package Content

Name	Description
dp_idealGas
dp_nominalDensityViscosity
dp_nominalPressureLossLawDensity
dp_pressureLossCoefficient
dp_volumeFlowRate

Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.PressureLoss.General.dp_idealGas

Calculation of a generic pressure loss for an ideal gas using mean density.

Restriction

This function shall be used inside of the restricted limits according to the referenced literature.

• ideal gas
• mean density of ideal gas

Calculation

The geometry parameters of energy devices necessary for the pressure loss calculations are often not exactly known. Therefore the modelling of the detailed pressure loss calculation has to be simplified.

The pressure loss dp for the compressible case [Mass flow rate = f(dp)] is determined by (Eq.1):

    m_flow = (R_s/Km)^(1/exp)*(rho_m)^(1/exp)*dp^(1/exp)

for the underlying base equation using ideal gas law as follows:

    dp^2 = p_2^2 - p_1^2 = Km*m_flow^exp*(T_2 + T_1)
    dp   = p_2 - p_1     = Km*m_flow^exp*T_m/p_m, Eq.2 with [dp] = Pa, [m_flow] = kg/s

so that the coefficient Km is calculated out of Eq.2:

    Km = dp*R_s*rho_m / m_flow^exp , [Km] = [Pa^2/{(kg/s)^exp*K}]

where the mean density rho_m is calculated according to the ideal gas law out of an arithmetic mean pressure and temperature:

   rho_m = p_m / (R_s*T_m) , p_m = (p_1 + p_2)/2 and T_m = (T_1 + T_2)/2.

with

exp	as exponent of pressure loss law [-],
dp	as pressure loss [Pa],
Km	as coefficient w.r.t. mass flow rate! [Km] = [Pa^2/{(kg/s)^exp*K}],
m_flow	as mass flow rate [kg/s],
p_m = (p_2 + p_1)/2	as mean pressure of ideal gas [Pa],
T_m = (T_2 + T_1)/2	as mean temperature of ideal gas [K],
rho_m = p_m/(R_s*T_m)	as mean density of ideal gas [kg/m3],
R_s	as specific gas constant of ideal gas [J/(kgK)],
V_flow	as volume flow rate of ideal gas [m^3/s].

Furthermore the coefficient Km can be defined more detailled w.r.t. the definition of pressure loss if Km is not given as (e.g., measured) value. Generally pressure loss can be calculated due to local losses Km,LOC or frictional losses Km,FRI .

Pressure loss due to local losses gives the following definition of Km :

    dp        = zeta_LOC * (rho_m/2)*velocity^2 is leading to
      Km,LOC  = (8/&Pi^2)*R_s*zeta_LOC/(d_hyd)^4, considering the cross sectional area of pipes.

and pressure loss due to friction is leading to

    dp        = lambda_FRI*L/d_hyd * (rho_m/2)*velocity^2
      Km,FRI  = (8/&Pi^2)*R_s*lambda_FRI*L/(d_hyd)^5, considering the cross sectional area of pipes.

with

dp	as pressure loss [Pa],
d_hyd	as hydraulic diameter of pipe [m],
Km,i	as coefficients w.r.t. mass flow rate! [Km] = [Pa^2/{(kg/s)^exp*K}],
lambda_FRI	as darcy friction factor [-],
L	as length of pipe [m],
rho_m = p_m/(R_s*T_m)	as mean density of ideal gas [kg/m3],
velocity	as mean velocity [m/s],
zeta_LOC	as local resistance coefficient [-].

Note that the variables of this function are delivered in SI units so that the coefficient Km shall be given in SI units too.

Verification

Compressible case [Mass flow rate = f(dp)]:

The mass flow rate m_flow for different coefficients Km as parameter is shown in dependence of its pressure loss dp in the figure below.

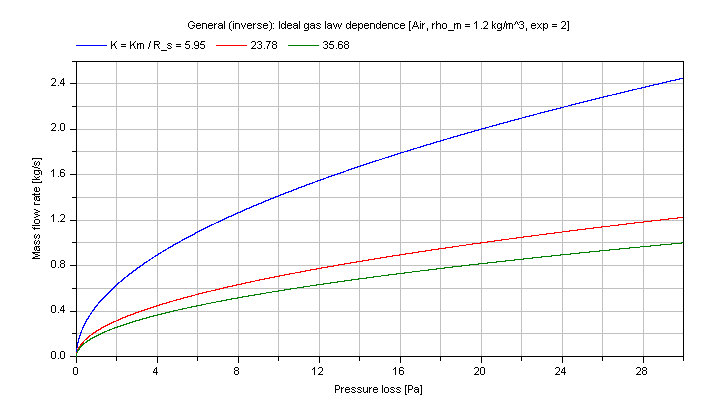
Note that the verification for dp_idealGas is also valid for this inverse calculation due to using the same functions.

References

Elmquist, H., M.Otter and S.E. Cellier:

Inline integration: A new mixed symbolic / numeric approach for solving differential-algebraic equation systems.. In Proceedings of European Simulation MultiConference, Praque, 1995.

Extends from Modelica.Icons.Information (Icon for general information packages).

Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.PressureLoss.General.dp_nominalDensityViscosity

Calculation of a generic pressure loss in dependence of nominal fluid variables (e.g., nominal density, nominal dynamic viscosity) at an operation point via interpolation. This generic function considers the pressure loss law via a pressure loss exponent and the influence of density and dynamic viscosity on pressure loss.

Calculation

The geometry parameters of energy devices necessary for the pressure loss calculations are often not exactly known. Therefore the modelling of the detailed pressure loss calculation has to be simplified. This function uses nominal variables (e.g., nominal pressure loss) at a known operation point of the energy device to interpolate the actual pressure loss according to a pressure loss law (exponent).

The generic pressure loss dp is determined for:

• compressible case [Mass flow rate = f(dp)]:

     m_flow = m_flow_nom*[(dp/dp_nom)*(rho/rho_nom)]^(1/exp)*(eta_nom/eta)^(exp_eta/exp)
     

• incompressible case [Pressure loss = f(m_flow)]:

     dp = dp_nom*(m_flow/m_flow_nom)^exp*(rho_nom/rho)*(eta/eta_nom)^exp_eta
     

with

dp	as pressure loss [Pa],
dp_nom	as nominal pressure loss [Pa],
eta	as dynamic viscosity of fluid [kg/(ms)].
eta_nom	as nominal dynamic viscosity of fluid [kg/(ms)].
m_flow	as mass flow rate [kg/s],
m_flow_nom	as nominal mass flow rate [kg/s],
exp	as exponent of pressure loss calculation [-],
exp_eta	as exponent of dynamic viscosity dependence [-],
rho	as fluid density [kg/m3],
rho_nom	as nominal fluid density [kg/m3].

To avoid numerical difficulties this pressure loss function is linear smoothed for

• small mass flow rates, where

      m_flow ≤ (0.01*rho/rho_nom*(1/eta*eta_nom)^(exp_eta))^(1/exp) and
    

• small pressure losses, where

      dp ≤ 0.01*dp_nom)
   

Note that the density (rho) and dynamic viscosity (eta) of the fluid are defined through the defintion of the kinematic viscosity (nue).

    nue = eta / rho

Therefore if you set both the exponent of dynamic viscosity (exp_eta == 1) and additionally a relation of density and dynamic viscosity there will be no difference for varying densities because the dynamic viscosities will vary in the same manner.

Verification

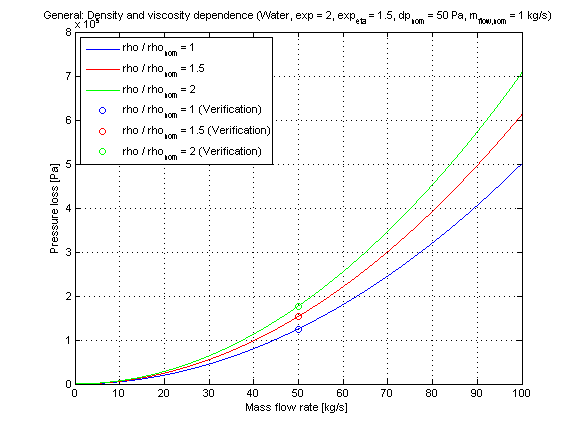
Incompressible case [Pressure loss = f(m_flow)]:

The generic pressure loss DP in dependence of the mass flow rate m_flow with different fluid densities and dynamic viscosity dependence as parameters is shown for a turbulent pressure loss regime (exp == 2) in the figure below.

Compressible case [Mass flow rate = f(dp)]:

The generic mass flow rate M_FLOW in dependence of the pressure loss dp at different fluid densities and dynamic viscosity as parameters is shown for a turbulent pressure loss regime (exp == 2) in the figure below.

References

Elmquist, H., M.Otter and S.E. Cellier:

Inline integration: A new mixed symbolic / numeric approach for solving differential-algebraic equation systems.. In Proceedings of European Simulation MultiConference, Praque, 1995.

Wischhusen, S.:

Dynamische Simulation zur wirtschaftlichen Bewertung von komplexen Energiesystemen.. PhD thesis, Technische Universität Hamburg-Harburg, 2005.

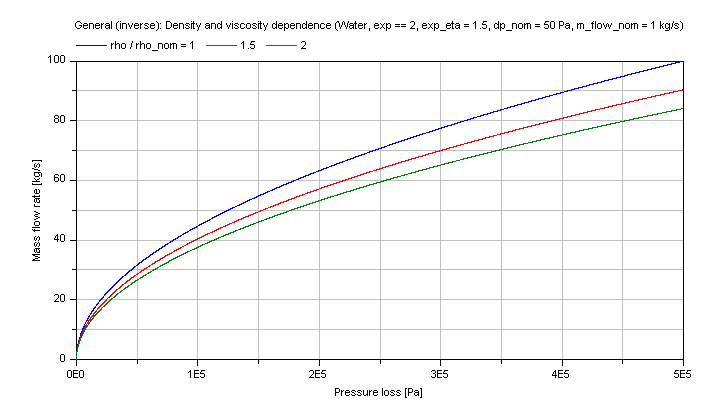
Extends from Modelica.Icons.Information (Icon for general information packages).

Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.PressureLoss.General.dp_nominalPressureLossLawDensity

Calculation of a generic pressure loss in dependence of nominal fluid variables (e.g., nominal density) via interpolation from an operation point. This generic function considers the pressure loss law via a nominal pressure loss (dp_nom), a pressure loss coefficient (zeta_TOT) and a pressure loss law exponent (exp) as well as the influence of density on pressure loss.

Calculation

The geometry parameters of energy devices necessary for the pressure loss calculations are often not exactly known. Therefore the modelling of the detailed pressure loss calculation have to be simplified. This function uses nominal variables (e.g., nominal pressure loss) at a known operation point of the energy device to interpolate the actual pressure loss according to a pressure loss law (exponent).

In the following the pressure loss dp is generally determined from a known operation point via a law of similarity:

   dp/dp_nom = (zeta_TOT/zeta_TOT_nom)*(rho/rho_nom)*(v/v_nom)^exp

with

dp	as pressure loss [Pa],
dp_nom	as nominal pressure loss [Pa],
m_flow	as mass flow rate [kg/s],
m_flow_nom	as nominal mass flow rate [kg/s],
exp	as exponent of pressure loss calculation [-],
rho	as fluid density [kg/m3],
rho_nom	as nominal fluid density [kg/m3],
v	as mean flow velocity [m/s],
v_nom	as nominal mean flow velocity [m/s],
zeta_TOT	as pressure loss coefficient [-],
zeta_TOT_nom	as nominal pressure loss coefficient [-].

The fraction of mean flow velocities (v/v_nom) can be calculated through its corresponding mass flow rates , densities and cross sectional areas:

   v/v_nom = (m_flow/m_flow_nom)*(A_cross_nom/A_cross)*(rho_nom/rho)

or through its corresponding volume flow rates , densities and cross sectional areas:

    v/v_nom = (V_flow/V_flow_nom)*(A_cross_nom/A_cross).

with

A_cross	as cross sectional area [m2],
A_cross_nom	as nominal cross sectional area [m2],
rho	as fluid density [kg/m3],
rho_nom	as nominal fluid density [kg/m3],
v	as mean flow velocity [m/s],
v_nom	as nominal mean flow velocity [m/s],
V_flow	as volume flow rate [m3/s],
V_flow_nom	as nominal volume flow rate [m3/s].

Here the compressible case [Mass flow rate = f(dp)] determines the unknown mass flow rate out of a given pressure loss:

   m_flow = m_flow_nom*(A_cross/A_cross_nom)*(rho_nom/rho)^(exp_density/exp)*[(dp/dp_nom)*(zeta_TOT_nom/zeta_TOT)]^(1/exp);

where the exponent for the fraction of densities is determined w.r.t. the chosen nominal mass flow rate or nominal volume flow rate to:

  exp_density = if NominalMassFlowRate == 1 then 1-exp else 1

with

NominalMassFlowRate	as reference for pressure loss law (mass flow rate of volume flow rate),
exp	as exponent of pressure loss calculation [-],
exp_density	as exponent for density [-].

To avoid numerical difficulties this pressure loss function is linear smoothed for small pressure losses, with

   dp ≤ 0.01*dp_nom

Note that the input and output arguments for functions throughout this library always use mass flow rates. Here you can choose NominalMassFlowRate == 1 for using a nominal mass flow rate or NominalMassFlowRate == 2 for using a nominal volume flow rate. The output argument will always be a mass flow rate for further use as flow model in a thermo-hydraulic framework.

Note that the pressure loss coefficients (zeta_TOT,zeta_TOT_nom) refer to its mean flow velocities (v,v_nom) in the pressure loss law to obtain its corresponding pressure loss.

Verification

Compressible case [Mass flow rate = f(dp)]:

The generic mass flow rate M_FLOW in dependence of the pressure loss dp is shown for a turbulent pressure loss regime (exp == 2) in the figure below.

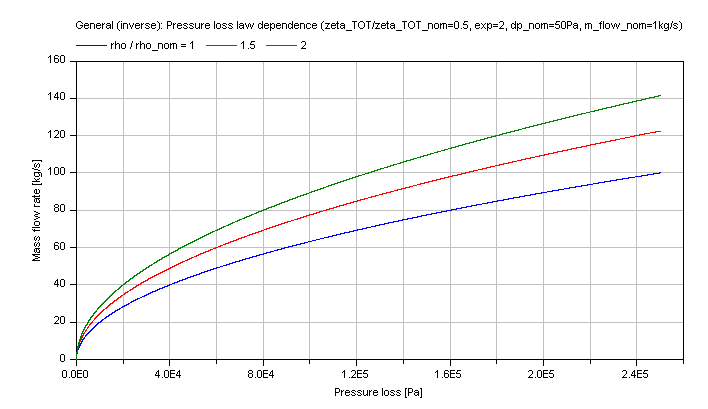
Note that the verification for dp_nominalPressureLossLawDensity is also valid for this inverse calculation due to using the same functions.

References

Elmquist, H., M.Otter and S.E. Cellier:

Inline integration: A new mixed symbolic / numeric approach for solving differential-algebraic equation systems.. In Proceedings of European Simulation MultiConference, Praque, 1995.

Wischhusen, S.:

Dynamische Simulation zur wirtschaftlichen Bewertung von komplexen Energiesystemen.. PhD thesis, Technische Universität Hamburg-Harburg, 2005.

Extends from Modelica.Icons.Information (Icon for general information packages).

Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.PressureLoss.General.dp_pressureLossCoefficient

Calculation of a generic pressure loss in dependence of a pressure loss coefficient.

Calculation

The mass flow rate m_flow is determined by:

    m_flow = rho*A_cross*(dp/(zeta_TOT *(rho/2))^0.5

with

A_cross	as cross sectional area [m2],
dp	as pressure loss [Pa],
rho	as density of fluid [kg/m3],
m_flow	as mass flow rate [kg/s],
zeta_TOT	as pressure loss coefficient [-].

Verification

Compressible case [Mass flow rate = f(dp)]:

The mass flow rate M_FLOW in dependence of the pressure loss dp for a constant pressure loss coefficient zeta_TOT is shown in the figure below.

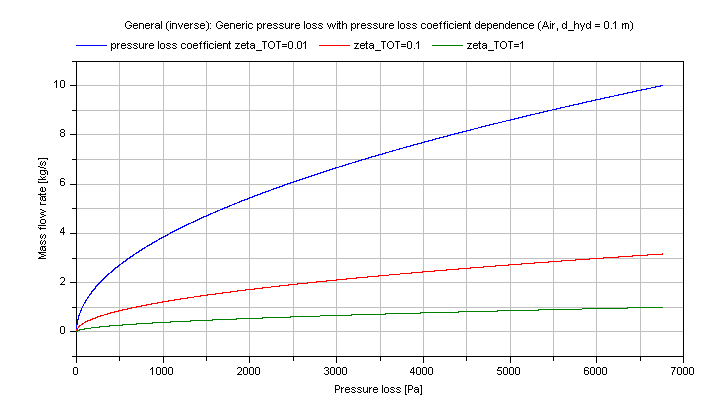
Note that the verification for dp_pressureLossCoefficient is also valid for this inverse calculation due to using the same functions.

References

Elmquist, H., M.Otter and S.E. Cellier:

Inline integration: A new mixed symbolic / numeric approach for solving differential-algebraic equation systems.. In Proceedings of European Simulation MultiConference, Praque, 1995.

Wischhusen, S.:

Dynamische Simulation zur wirtschaftlichen Bewertung von komplexen Energiesystemen.. PhD thesis, Technische Universität Hamburg-Harburg, 2005.

Extends from Modelica.Icons.Information (Icon for general information packages).

Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.PressureLoss.General.dp_volumeFlowRate

Calculation of a generic pressure loss with linear or quadratic dependence on volume flow rate.

Calculation

The geometry parameters of energy devices necessary for the pressure loss calculations are often not exactly known. Therefore the modelling of the detailed pressure loss calculation has to be simplified. This function uses as quadratic dependence of the pressure loss on the volume flow rate.

The mass flow rate m_flow for the compressible case [Mass flow rate = f(dp)] is determined to [see Wischhusen] :

 m_flow = rho*[-b/(2a) + {[b/(2a)]^2 + dp/a}^0.5]

with

a	as quadratic coefficient [Pa*s^2/m^6],
b	as linear coefficient [Pa*s/m3],
dp	as pressure loss [Pa],
m_flow	as mass flow rate [kg/s],
rho	as density of fluid [kg/m3].

Note that the coefficients a,b have to be positive values so that there will be a positive (linear or quadratic) pressure loss at positive volume flow rate and vice versa.

Verification

Compressible case [Mass flow rate = f(dp)]:

The generic pressure loss dp for different coefficients a as parameter is shown in dependence of the volume flow rate V_flow in the figure below.

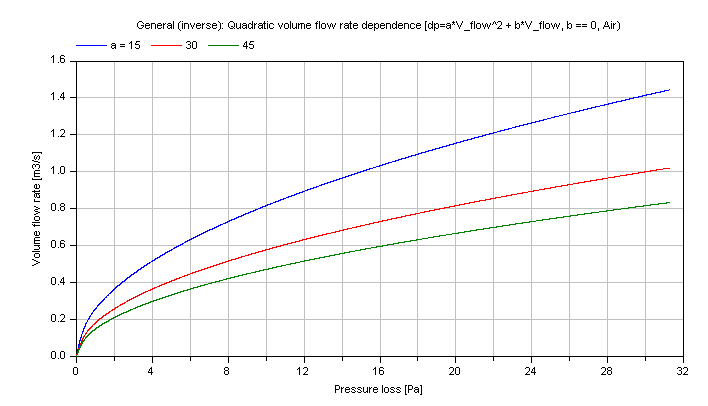
Note that the verification for dp_volumeFlowRate is also valid for this inverse calculation due to using the same functions.

References

Elmquist, H., M.Otter and S.E. Cellier:

Inline integration: A new mixed symbolic / numeric approach for solving differential-algebraic equation systems.. In Proceedings of European Simulation MultiConference, Praque, 1995.

Wischhusen, S.:

Dynamische Simulation zur wirtschaftlichen Bewertung von komplexen Energiesystemen.. PhD thesis, Technische Universität Hamburg-Harburg, 2005.

Extends from Modelica.Icons.Information (Icon for general information packages).