Modelica.Electrical.QuasiStationary.UsersGuide.Overview

The Modelica.Electrical.QuasiStationary library addresses the analysis of electrical circuits with purely sinusoidal voltages and currents. The main characteristics of the library are:

• Only pure sinusoidal voltages and currents are taken into account. Higher harmonic voltages and currents are not considered.
• Any electrical transient effects are negelcted.
• The electrical components of this library are strictly linear.
• The angular frequency omega of the voltages and currents of a circuit are determined from a reference angle gamma by means of omega = der(gamma).
• The reference angle gamma is not a global quantity since it propagated through the connector. Therefore, independent circuits of different frequencies can be modeled in one model.
• The connectors contain the real and the imaginary part of the voltage and the current RMS phasors

The main intention of this library is the modeling of quasi stationary behavior of single and multi phase AC circuits with fixed and variable frequency. Quasi stationary theory and applications can be found in [Dorf1993], [Burton1994], [Landolt1936], [Philippow1967], [Weyh1967], [Vaske1973].

Note

A general electrical circuit can be a DC circuit, an AC circuit with periodic sinusoidal or non-sinusodial voltages and currents or a transient circuit without particular waveform of voltages and currents. Therefore a coupling model between a quasi stationary circuit and a general (transient) electrical circuit has to be designed carefully taking the specific application into account. As an exmaple, you may look at the ideal AC DC converter, which is used in the rectifier example.

Extends from Modelica.Icons.Information (Icon for general information packages).

Package Content

Name	Description
Introduction	Introduction to phasors
ACCircuit	AC circuit
Power	Real and reactive power
ReferenceSystem	Reference system

Modelica.Electrical.QuasiStationary.UsersGuide.Overview.Introduction

The purely sinusoidal voltage

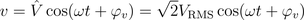
in the time domain can be represented by a complex rms phasor

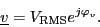
For these quasi stationary phasor the following relationship applies:

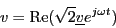
This equation is also illustrated in Fig. 1.

Fig. 1: Relationship between voltage phasor and time domain voltage

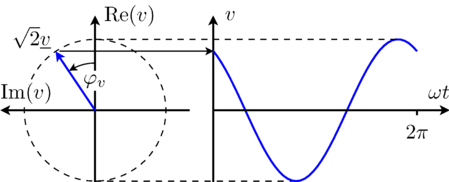
From the above equation it is obvious that for t = 0 the time domain voltage is v = cos(φ_v). The complex representation of the phasor corresponds with this instance, too, since the phasor is leading the real axis by the angle φ_v.

The explanation given for sinusoidal voltages can certainly also be applied to sinusoidal currents.

See also

Extends from Modelica.Icons.Information (Icon for general information packages).

Modelica.Electrical.QuasiStationary.UsersGuide.Overview.ACCircuit

A simple example of a series connection of a resistor, an inductor and a capacitor as depicted in Fig. 1 should be explained in the following. For various frequencies, the voltage drops across the resistor, the inductor and the capacitor should be determined.

Fig. 1: Series AC circuit of a resistor and an inductor at variable frequency

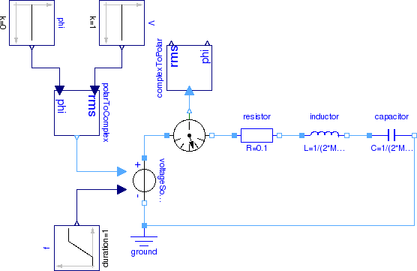
The voltage drop across the resistor

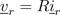
and the inductor

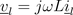
and the capacitor

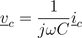
add up to the total voltage

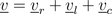
as illustrated in the phasor diagram of Fig. 2.

Fig. 2: Phasor diagram of a resistor and inductance series connection

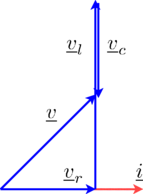
Due to the series connection of the resistor, inductor and capacitor, the three currents are all equal:

See also

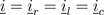
Extends from Modelica.Icons.Information (Icon for general information packages).

Modelica.Electrical.QuasiStationary.UsersGuide.Overview.Power

For periodic waveforms, the average value of the instantaneous power is real power P. Reactive power Q is a term associated with inductors and capacitors. For pure inductors and capacitors, real power is equal to zero. Yet, there is instantaneous power exchanged with connecting network.

Power of a resistor

The instantaneous voltage and current are in phase:

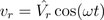
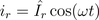
Therefore, the instantaneous power is

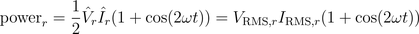
A graphical representation of these equations is depicted in Fig. 1

Fig. 1: Instantaneous voltage, current of power of a resistor

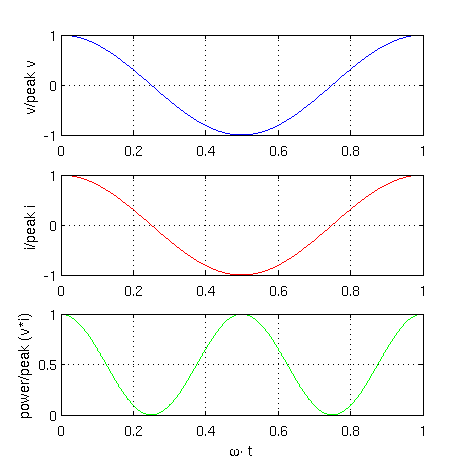
Real power of the resistor is the average of instantaneous power:

Power of an inductor

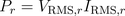
The instantaneous voltage leads the current by a quarter of the period:

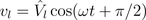
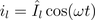
Therefore, the instantaneous power is

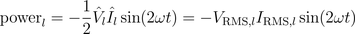
A graphical representation of these equations is depicted in Fig. 2

Fig. 2: Instantaneous voltage, current of power of an inductor

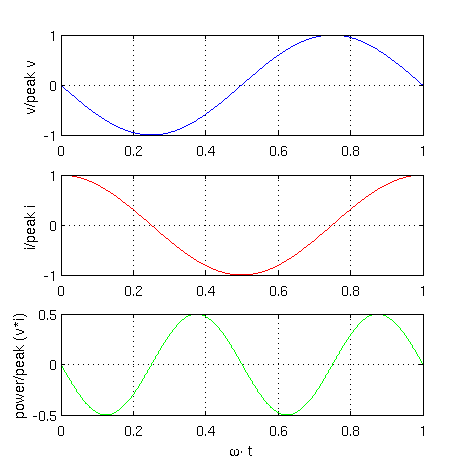
Reqactive power of the inductor is:

Power of a capacitor

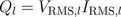
The instantaneous voltage lags the current by a quarter of the period:

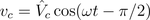
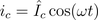
Therefore, the instantaneous power is

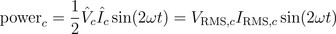
A graphical representation of these equations is depicted in Fig. 3

Fig. 3: Instantaneous voltage, current of power of a capacitor

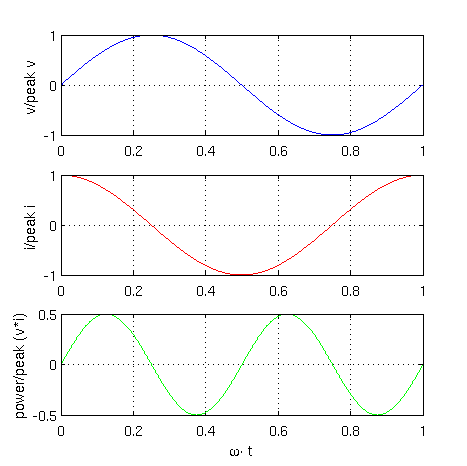
Reqactive power of the capacitor is:

Complex apparent power

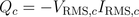
For an arbitrary component with two pins, real and reactive power can be determined by the complex phasors:

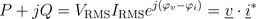
In this equation ^* represents the conjugate complex operator

See also

Extends from Modelica.Icons.Information (Icon for general information packages).

Modelica.Electrical.QuasiStationary.UsersGuide.Overview.ReferenceSystem

The reference angle gamma:

• defines the angular frequency omega of the voltages and currents of a circuit by means of omega = der(gamma).
• is not a global quantity since it propagated through the connector. Therefore, independent circuits of different frequencies can be modeled in one model.
• is present only once in a multiphase connector; a multiphase component has only one reference angle common to all phases.
• can be either constant or variable, but it has to be consistent in one contiguous circuit.
• is defined by the sources.

Designing new components, the guidelines of the Modelica Specification dealing with Overconstrained Equation Operators for Connection Graphs have to be taken into account.

See also

Extends from Modelica.Icons.Information (Icon for general information packages).