This package hosts basic models for quasi stationary single phase circuits. Quasi stationary theory for single phase circuits can be found in the references.
Extends from Modelica.Icons.Package (Icon for standard packages).
| Name | Description |
|---|---|
| Electrical ground | |
| Singlephase linear resistor | |
| Singlephase linear conductor | |
| Singlephase linear capacitor | |
| Singlephase linear inductor | |
| Singlephase variable resistor | |
| Singlephase variable conductor | |
| Singlephase variable capacitor | |
| Singlephase variable inductor |
 Modelica.Electrical.QuasiStationary.SinglePhase.Basic.Ground
Modelica.Electrical.QuasiStationary.SinglePhase.Basic.Ground

Ground of a single phase circuit. The potential at the ground node is zero. Every electrical circuit, e.g., a series resonance example, has to contain at least one ground object.
| Type | Name | Description |
|---|---|---|
| PositivePin | pin |
model Ground "Electrical ground"Interfaces.PositivePin pin; equation Connections.potentialRoot(pin.reference, 256); if Connections.isRoot(pin.reference) then pin.reference.gamma = 0; end if; pin.v = Complex(0);end Ground;
 Modelica.Electrical.QuasiStationary.SinglePhase.Basic.Resistor
Modelica.Electrical.QuasiStationary.SinglePhase.Basic.Resistor

The linear resistor connects the complex voltage v with the complex current i by i*R = v. The resistance R is allowed to be positive, zero, or negative.
The resistor model also has an optional conditional heat port. A linear temperature dependency of the resistance for an enabled heat port is also taken into account.
Conductor, Capacitor, Inductor, Variable resistor, Variable conductor, Variable capacitor, Variable inductor
Extends from Interfaces.OnePort (Two pins, current through), Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network).
| Type | Name | Default | Description |
|---|---|---|---|
| Resistance | R_ref | Reference resistance at T_ref [Ohm] | |
| Temperature | T_ref | 293.15 | Reference temperature [K] |
| LinearTemperatureCoefficient | alpha_ref | 0 | Temperature coefficient of resistance (R_actual = R_ref*(1 + alpha_ref*(heatPort.T - T_ref)) [1/K] |
| Boolean | useHeatPort | false | =true, if HeatPort is enabled |
| Temperature | T | T_ref | Fixed device temperature if useHeatPort = false [K] |
| Type | Name | Description |
|---|---|---|
| PositivePin | pin_p | Positive pin |
| NegativePin | pin_n | Negative pin |
| HeatPort_a | heatPort |
model Resistor "Singlephase linear resistor"
extends Interfaces.OnePort;
import Modelica.ComplexMath.real;
import Modelica.ComplexMath.conj;
parameter Modelica.SIunits.Resistance R_ref(start=1)
"Reference resistance at T_ref";
parameter Modelica.SIunits.Temperature T_ref=293.15 "Reference temperature";
parameter Modelica.SIunits.LinearTemperatureCoefficient alpha_ref=0
"Temperature coefficient of resistance (R_actual = R_ref*(1 + alpha_ref*(heatPort.T - T_ref))";
extends Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort(T = T_ref);
Modelica.SIunits.Resistance R_actual
"Resistance = R_ref*(1 + alpha_ref*(heatPort.T - T_ref))";
equation
assert((1 + alpha_ref*(T_heatPort - T_ref)) >= Modelica.Constants.eps, "Temperature outside scope of model!");
R_actual = R_ref*(1 + alpha_ref*(T_heatPort - T_ref));
v = R_actual*i;
LossPower = real(v*conj(i));
end Resistor;
 Modelica.Electrical.QuasiStationary.SinglePhase.Basic.Conductor
Modelica.Electrical.QuasiStationary.SinglePhase.Basic.Conductor

The linear conductor connects the voltage v with the current i by i = v*G. The conductance G is allowed to be positive, zero, or negative.
The conductor model also has an optional conditional heat port. A linear temperature dependency of the resistance for an enabled heat port is also taken into account.
Resistor, Capacitor, Inductor, Variable resistor, Variable conductor, Variable capacitor, Variable inductor
Extends from Interfaces.OnePort (Two pins, current through), Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network).
| Type | Name | Default | Description |
|---|---|---|---|
| Conductance | G_ref | Reference conductance at T_ref [S] | |
| Temperature | T_ref | 293.15 | Reference temperature [K] |
| LinearTemperatureCoefficient | alpha_ref | 0 | Temperature coefficient of conductance (G_actual = G_ref/(1 + alpha_ref*(heatPort.T - T_ref)) [1/K] |
| Boolean | useHeatPort | false | =true, if HeatPort is enabled |
| Temperature | T | T_ref | Fixed device temperature if useHeatPort = false [K] |
| Type | Name | Description |
|---|---|---|
| PositivePin | pin_p | Positive pin |
| NegativePin | pin_n | Negative pin |
| HeatPort_a | heatPort |
model Conductor "Singlephase linear conductor"
extends Interfaces.OnePort;
import Modelica.ComplexMath.real;
import Modelica.ComplexMath.conj;
parameter Modelica.SIunits.Conductance G_ref(start=1)
"Reference conductance at T_ref";
parameter Modelica.SIunits.Temperature T_ref=293.15 "Reference temperature";
parameter Modelica.SIunits.LinearTemperatureCoefficient alpha_ref=0
"Temperature coefficient of conductance (G_actual = G_ref/(1 + alpha_ref*(heatPort.T - T_ref))";
extends Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort(T = T_ref);
Modelica.SIunits.Conductance G_actual
"Conductance = G_ref/(1 + alpha_ref*(heatPort.T - T_ref))";
equation
assert((1 + alpha_ref*(T_heatPort - T_ref)) >= Modelica.Constants.eps, "Temperature outside scope of model!");
G_actual = G_ref/(1 + alpha_ref*(T_heatPort - T_ref));
i = G_actual*v;
LossPower = real(v*conj(i));
end Conductor;
 Modelica.Electrical.QuasiStationary.SinglePhase.Basic.Capacitor
Modelica.Electrical.QuasiStationary.SinglePhase.Basic.Capacitor

The linear capacitor connects the voltage v with the current i by i = j*ω*C*v. The capacitance C is allowed to be positive, zero, or negative.
Resistor, Conductor, Inductor, Variable resistor, Variable conductor, Variable capacitor, Variable inductor
Extends from Interfaces.OnePort (Two pins, current through).
| Type | Name | Default | Description |
|---|---|---|---|
| Capacitance | C | Capacitance [F] |
| Type | Name | Description |
|---|---|---|
| PositivePin | pin_p | Positive pin |
| NegativePin | pin_n | Negative pin |
model Capacitor "Singlephase linear capacitor" extends Interfaces.OnePort; import Modelica.ComplexMath.j; parameter Modelica.SIunits.Capacitance C(start=1) "Capacitance"; equation i = j*omega*C*v;end Capacitor;
 Modelica.Electrical.QuasiStationary.SinglePhase.Basic.Inductor
Modelica.Electrical.QuasiStationary.SinglePhase.Basic.Inductor

The linear inductor connects the voltage v with the current i by v = j*ω*L*i. The Inductance L is allowed to be positive, zero, or negative.
Resistor, Conductor, Capacitor, Variable resistor, Variable conductor, Variable capacitor, Variable inductor
Extends from Interfaces.OnePort (Two pins, current through).
| Type | Name | Default | Description |
|---|---|---|---|
| Inductance | L | Inductance [H] |
| Type | Name | Description |
|---|---|---|
| PositivePin | pin_p | Positive pin |
| NegativePin | pin_n | Negative pin |
model Inductor "Singlephase linear inductor" extends Interfaces.OnePort; import Modelica.ComplexMath.j; parameter Modelica.SIunits.Inductance L(start=1) "Inductance"; equation v = j*omega*L*i;end Inductor;
 Modelica.Electrical.QuasiStationary.SinglePhase.Basic.VariableResistor
Modelica.Electrical.QuasiStationary.SinglePhase.Basic.VariableResistor
The linear resistor connects the voltage v with the current i by i*R = v. The resistance R is given as input signal.
The variable resistor model also has an optional conditional heat port. A linear temperature dependency of the resistance for an enabled heat port is also taken into account.
A zero crossing of the R signal could cause singularities due to the actual structure of the connected network.
The variable resistor model also has an optional conditional heat port. A linear temperature dependency of the resistance for an enabled heat port is also taken into account.
Resistor, Conductor, Capacitor, Inductor, Variable conductor, Variable capacitor, Variable inductor
Extends from Interfaces.OnePort (Two pins, current through), Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network).
| Type | Name | Default | Description |
|---|---|---|---|
| Temperature | T_ref | 293.15 | Reference temperature [K] |
| LinearTemperatureCoefficient | alpha_ref | 0 | Temperature coefficient of resistance (R_actual = R_ref*(1 + alpha_ref*(heatPort.T - T_ref)) [1/K] |
| Boolean | useHeatPort | false | =true, if HeatPort is enabled |
| Temperature | T | T_ref | Fixed device temperature if useHeatPort = false [K] |
| Type | Name | Description |
|---|---|---|
| PositivePin | pin_p | Positive pin |
| NegativePin | pin_n | Negative pin |
| HeatPort_a | heatPort | |
| input RealInput | R_ref |
model VariableResistor "Singlephase variable resistor"
extends Interfaces.OnePort;
import Modelica.ComplexMath.real;
import Modelica.ComplexMath.conj;
parameter Modelica.SIunits.Temperature T_ref=293.15 "Reference temperature";
parameter Modelica.SIunits.LinearTemperatureCoefficient alpha_ref=0
"Temperature coefficient of resistance (R_actual = R_ref*(1 + alpha_ref*(heatPort.T - T_ref))";
extends Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort(T = T_ref);
Modelica.SIunits.Resistance R_actual
"Resistance = R_ref*(1 + alpha_ref*(heatPort.T - T_ref))";
Modelica.Blocks.Interfaces.RealInput R_ref;
equation
assert((1 + alpha_ref*(T_heatPort - T_ref)) >= Modelica.Constants.eps, "Temperature outside scope of model!");
R_actual = R_ref*(1 + alpha_ref*(T_heatPort - T_ref));
v = R_actual*i;
LossPower = real(v*conj(i));
end VariableResistor;
 Modelica.Electrical.QuasiStationary.SinglePhase.Basic.VariableConductor
Modelica.Electrical.QuasiStationary.SinglePhase.Basic.VariableConductor
The linear conductor connects the voltage v with the current i by i = G*v. The conductance G is given as input signal.
The variable conductor model also has an optional conditional heat port. A linear temperature dependency of the resistance for an enabled heat port is also taken into account.
Resistor, Conductor, Capacitor, Inductor, Variable resistor, Variable capacitor, Variable inductor
Extends from Interfaces.OnePort (Two pins, current through), Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network).
| Type | Name | Default | Description |
|---|---|---|---|
| Temperature | T_ref | 293.15 | Reference temperature [K] |
| LinearTemperatureCoefficient | alpha_ref | 0 | Temperature coefficient of conductance (G_actual = G_ref/(1 + alpha_ref*(heatPort.T - T_ref)) [1/K] |
| Boolean | useHeatPort | false | =true, if HeatPort is enabled |
| Temperature | T | T_ref | Fixed device temperature if useHeatPort = false [K] |
| Type | Name | Description |
|---|---|---|
| PositivePin | pin_p | Positive pin |
| NegativePin | pin_n | Negative pin |
| HeatPort_a | heatPort | |
| input RealInput | G_ref |
model VariableConductor "Singlephase variable conductor"
extends Interfaces.OnePort;
import Modelica.ComplexMath.real;
import Modelica.ComplexMath.conj;
parameter Modelica.SIunits.Temperature T_ref=293.15 "Reference temperature";
parameter Modelica.SIunits.LinearTemperatureCoefficient alpha_ref=0
"Temperature coefficient of conductance (G_actual = G_ref/(1 + alpha_ref*(heatPort.T - T_ref))";
extends Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort(T = T_ref);
Modelica.SIunits.Conductance G_actual
"Conductance = G_ref/(1 + alpha_ref*(heatPort.T - T_ref))";
Modelica.Blocks.Interfaces.RealInput G_ref;
equation
assert((1 + alpha_ref*(T_heatPort - T_ref)) >= Modelica.Constants.eps, "Temperature outside scope of model!");
G_actual = G_ref/(1 + alpha_ref*(T_heatPort - T_ref));
i = G_actual*v;
LossPower = real(v*conj(i));
end VariableConductor;
 Modelica.Electrical.QuasiStationary.SinglePhase.Basic.VariableCapacitor
Modelica.Electrical.QuasiStationary.SinglePhase.Basic.VariableCapacitor

The linear capacitor connects the voltage v with the current i by i = j*ω*C*v. The capacitance C is given as input signal.
The abstraction of a variable capacitor at quasi stationary operation assumes:
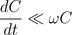 .
.
Resistor, Conductor, Capacitor, Inductor, Variable resistor, Variable conductor, Variable inductor
Extends from Interfaces.OnePort (Two pins, current through).
| Type | Name | Description |
|---|---|---|
| PositivePin | pin_p | Positive pin |
| NegativePin | pin_n | Negative pin |
| input RealInput | C |
model VariableCapacitor "Singlephase variable capacitor" extends Interfaces.OnePort; import Modelica.ComplexMath.j;Modelica.Blocks.Interfaces.RealInput C; equation i = j*omega*C*v;end VariableCapacitor;
 Modelica.Electrical.QuasiStationary.SinglePhase.Basic.VariableInductor
Modelica.Electrical.QuasiStationary.SinglePhase.Basic.VariableInductor

The linear inductor connects the branch voltage v with the branch current i by v = j*ω*L*i. The inductance L is given as input signal.
The abstraction of a variable inductor at quasi stationary operation assumes:
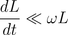
Resistor, Conductor, Capacitor, Inductor, Variable resistor, Variable conductor, Variable capacitor
Extends from Interfaces.OnePort (Two pins, current through).
| Type | Name | Description |
|---|---|---|
| PositivePin | pin_p | Positive pin |
| NegativePin | pin_n | Negative pin |
| input RealInput | L |
model VariableInductor "Singlephase variable inductor" extends Interfaces.OnePort; import Modelica.ComplexMath.j;Modelica.Blocks.Interfaces.RealInput L; equation v = j*omega*L*i;end VariableInductor;