Modelica.Media.UsersGuide.MediumDefinition

If a new medium model shall be introduced, copy package Modelica.Media.Interfaces.TemplateMedium to the desired location, remove the "partial" keyword from the package and provide the information that is requested in the comments of the Modelica source. A more detailed description for the different parts of the TemplateMedium package is given here:

Package Content

Name Description

BasicStructure Basic structure

BasicDefinition Basic definition

MultipleSubstances Multiple Substances

SpecificEnthalpyAsFunction Specific enthalpy as function

StaticStateSelection Static State Selection

TestOfMedium Test of medium

Name	Description
BasicStructure	Basic structure
BasicDefinition	Basic definition
MultipleSubstances	Multiple Substances
SpecificEnthalpyAsFunction	Specific enthalpy as function
StaticStateSelection	Static State Selection
TestOfMedium	Test of medium

Modelica.Media.UsersGuide.MediumDefinition.BasicStructure

A medium model of Modelica.Media is essentially a package that contains the following definitions:

Definition of constants, such as the medium name.
A model in the package that contains the 3 basic thermodynamic equations that relate the 5+nXi primary medium variables.
Optional functions to compute medium properties that are only needed in certain circumstances, such as dynamic viscosity. These optional functions need not be provided by every medium model.
Type definitions, which are adapted to the particular medium. For example, a type Temperature is defined where the attributes min and max define the validity region of the medium, and a suitable default start value is given. In a device model, it is advisable to use these type definitions, e.g., for parameters, in order that medium limits are checked as early as possible, and that iteration variables of non-linear systems of equations get reasonable start values.

Note, although we use the term medium model, it is actually a Modelica package that contains all the constants and definitions required for a complete medium model. The basic interface to a medium is defined by Modelica.Media.Interfaces.PartialMedium that has the following structure:

partial package PartialMedium
  import SI = Modelica.SIunits;
  constant String           mediumName = "";
  constant String           substanceNames[:] = {mediumName};
  constant String           extraPropertiesNames[:] = fill("",0);
  constant Boolean          singleState = false;
  constant Boolean          reducedX = true;
  constant Boolean          fixedX = false;
  constant AbsolutePressure reference_p = 101325;
  constant MassFraction     reference_X[nX]=fill(1/nX,nX);
  constant AbsolutePressure p_default = 101325;
  constant Temperature      T_default = Modelica.SIunits.Conversions.from_degC(20);
  constant SpecificEnthalpy h_default =
                            specificEnthalpy_pTX(p_default, T_default, X_default);
  constant MassFraction     X_default[nX]=reference_X;
  final constant Integer    nS  = size(substanceNames,1);
  final constant Integer    nX  = nS;
  final constant Integer    nXi = if fixedX then 0
                                  else if reducedX or nS == 1
                                  then nS-1 else nS;
  final constant Integer    nC  = size(extraPropertiesNames,1);
  constant FluidConstants[nS] fluidConstants;

  replaceable record BasePropertiesRecord
    AbsolutePressure p;
    Density d;
    Temperature T;
    SpecificEnthalpy h;
    SpecificInternalEnergy u;
    MassFraction[nX] X;
    MassFraction[nXi] Xi;
    SpecificHeatCapacity R;
    MolarMass MM;
  end BasePropertiesRecord;

  replaceable partial model BaseProperties
    extends BasePropertiesRecord;
    ThermodynamicState state;
    parameter Boolean preferredMediumStates=false;
    SI.Conversions.NonSIunits.Temperature_degC T_degC =
       Modelica.SIunits.Conversions.to_degC(T)
    SI.Conversions.NonSIunits.Pressure_bar p_bar =
       Modelica.SIunits.Conversions.to_bar(p)
  equation
    Xi = X[1:nXi];
    if nX > 1 then
       if fixedX then
          X = reference_X;
       elseif reducedX then
          X[nX] = 1 - sum(Xi);
       end if;
    end if;
    // equations such as
    //    d = d(p,T);
    //    u = u(p,T);
    //    h = u + p/d;
    //    state.p = p;
    //    state.T = T;
    // will go here in actual media implementations, but are not present
    // in the base class since the ThermodynamicState record is still empty
   end BaseProperties

  replaceable record ThermodynamicState
     // there are no "standard" thermodynamic variables in the base class
     // but they will be defined here in actual media extending PartialMedium
     // Example:
     //    AbsolutePressure p "Absolute pressure of medium";
     //    Temperature      T "Temperature of medium";
  end ThermodynamicState;

  // optional medium properties
  replaceable partial function dynamicViscosity
    input  ThermodynamicState state;
    output DynamicViscosity eta;
  end dynamicViscosity;

  // other optional functions

  // medium specific types
  type AbsolutePressure = SI.AbsolutePressure (
                               min     = 0,
                               max     = 1.e8,
                               nominal = 1.e5,
                               start   = 1.e5);
  type DynamicViscosity = ...;
  // other type definitions
end PartialMedium;

We will discuss all parts of this package in the following paragraphs. An actual medium model should extend from PartialMedium and has to provide implementations of the various parts.

Some of the constants at the beginning of the package do not have a value yet (this is valid in Modelica), but a value has to be provided when extending from package PartialMedium. A given value can be modified until the model is translated or the final prefix is set. The reason to use constants instead of parameters in the model BaseProperties is that some of these constants are used in a context where parameters are not allowed. For example, in connector definitions the number of independent mass fractions nXi is used as dimension of a vector Xi. When defining the connector, only constants in packages can be accessed, but not parameters in a model, because a connector cannot contain an instance of BaseProperties.

The record BasePropertiesRecord contains the variables primarily used in balance equations. Three equations for these variables have to be provided by every medium in model BaseProperties, plus two equations for the gas constant and the molar mass.

Optional medium properties are defined by functions, such as the function dynamicViscosity (see code Section above) to compute the dynamic viscosity. The argument of those functions is the ThermodynamicState record, defined in BaseProperties, which contains the minimum number of thermodynamic variables needed as an input to compute all the optional properties. This construction simplifies the usage considerably as demonstrated in the following code fragment:

  replaceable package Medium = Modelica.Media.Interfaces.PartialMedium;
  Medium.BaseProperties   medium;
  Medium.DynamicViscosity eta;
  ...
  U   = m*medium.u; //Internal energy
  eta = Medium.dynamicViscosity(medium.state);

Medium is the medium package that satisfies the requirements of a PartialMedium (when using the model above, a value for Medium has to be provided by a redeclaration). The medium component is an instance of the model Medium.BaseProperties and contains the core medium equations. Variables in this model can be accessed just by dot-notation, such as medium.u or medium.T. If an optional medium variable has to be computed, the corresponding function from the actual Medium package is called, such as Medium.dynamicViscosity. The medium.state vector can be given as input argument to this function, and its fields are kept consistent to those of BaseProperties by suitable equations, contained in BaseProperties itself (see above).

If a medium model does not provide implementations of all optional functions and one of these functions is called in a model, an error occurs during translation since the optional functions which have not been redeclared have the partial attribute. For example, if function dynamicViscosity is not provided in the medium model when it is used, only simple pressure drop loss models without a reference to the viscosity can be used and not the sophisticated ones.

At the bottom of the PartialMedium package type declarations are present, that are used in all other parts of the PartialMedium package and that should be used in all models and connectors where a medium model is accessed. The reason is that minimum, maximum, nominal, and start values are defined and these values can be adapted to the particular medium at hand. For example, the nominal value of AbsolutePressure is 10⁵ Pa. If a simple model of water steam is used that is only valid above 100 °C, then the minimum value in the Temperature type should be set to this value. The minimum and maximum values are also important for parameters in order to get an early message if data outside of the validity region is given. The nominal attribute is important as a scaling value if the variable is used as a state in a differential equation or as an iteration variable in a non-linear system of equations. The start attribute can be very useful to provide a meaningful default start or guess value if the variable is used, e.g., as iteration variable in a non-linear system of equations. Note, that all these attributes can be set specifically for a medium in the following way:

package MyMedium
  extends Modelica.Media.Interfaces.PartialMedium(
     ...
     Temperature(min=373));
end MyMedium;

The type PartialMedium.MassFlowRate is defined as

type MassFlowRate = Modelica.SIunits.MassFlowRate
     (quantity = "MassFlowRate." + mediumName);

Note that the constant mediumName, that has to be defined in every medium model, is used in the quantity attribute. For example, if mediumName = SimpleLiquidWater, then the quantity attribute has the value MassFlowRate.SimpleLiquidWater. This type should be used in a connector definition of a fluid library:

connector FluidPort
  replaceable package Medium = Modelica.Media.Interfaces.PartialMedium;
  flow Medium.MassFlowRate m_flow;
  ...
end FluidPort;

In the model where this connector is used, the actual Medium has to be defined. Connectors can only be connected together, if the corresponding attributes are either not defined or have identical values. Since mediumName is part of the quantity attribute of MassFlowRate, it is not possible to connect connectors with different media models together. In Dymola this is already checked when models are connected together in the diagram layer of the graphical user interface.

Modelica.Media.UsersGuide.MediumDefinition.BasicDefinition

Let's now walk through the definition of a new medium model. Please refer to Modelica.Media.Interfaces.TemplateMedium to obtain a template of the new medium model code. For the moment being, consider a single-substance medium model.

The new medium model is obtained by extending Modelica.Media.Interfaces.PartialMedium, and setting the following package constants:

mediumName is a String containing the name of the medium.
substancesNames is a vector of strings containing the names of the substances that make up the medium. In this case, it will contain only mediumName.
singleState can be set to true if u and d in BaseProperties do not depend on pressure. In other words, density does not depend on pressure (incompressible fluid), and it is assumed that also u does not depend on pressure. This setting can be useful for fluids having high density and low compressibility (e.g., liquids at moderate pressure); fast states resulting from the low compressibility effects are automatically avoided.
reducedX = true for single-substance media, which do not need mass fractions at all.

It is also possible to change the default min, max, nominal, and start attributes of Medium-defined types (see TemplateMedium).

All other package constants, such as nX, nXi, nS, are automatically set by the declarations of the base package Interfaces.PartialMedium.

The second step is to provide an implementation to the BaseProperties model, partially defined in the base class Interfaces.PartialMedium. In the case of single-substance media, two independent state variables must be selected among p, T, d, u, h, and three equations must be written to provide the values of the remaining variables. Two equations must then be added to compute the molar mass MM and the gas constant R.

The third step is to consider the optional functions that are going to be implemented, among the partial functions defined by the base class PartialMedium. A minimal set of state variables that could be provided as an input to all those functions must be selected, and included in the redeclaration of the ThermodynamicState record. Subsequently, equations must be added to BaseProperties in order that the instance of that record inside BaseProperties (named "state") is kept updated. For example, assume that all additional properties can be computed as a function of p and T. Then, ThermodynamicState should be redclared as follows:

  redeclare replaceable record ThermodynamicState
    AbsolutePressure p "Absolute pressure of medium";
    Temperature T "Temperature of medium";
  end ThermodynamicState;

and the following equations should be added to BaseProperties:

  state.p = p;
  state.T = T;

The additional functions can now be implemented by redeclaring the functions defined in the base class and adding their algorithms, e.g.:

    redeclare function extends dynamicViscosity "Return dynamic viscosity"
    algorithm
      eta := 10 - state.T*0.3 + state.p*0.2;
    end dynamicViscosity;

Modelica.Media.UsersGuide.MediumDefinition.MultipleSubstances

When writing the model of a multiple-substance medium, a fundamental issue concerns how to consider the mass fractions of the fluid. If there are nS substances, there are also nS mass fractions; however, one of them is redundant, as sum(X) = 1. Therefore there are basically two options, concerning the number of independent mass fractions nXi:

Reduced-state models: reducedX = true and nXi = nS - 1. In this case, the number of independent mass fractions nXi is the minimum possible. The full state vector X is provided by equations declared in the base class Interfaces.PartialMedium.BaseProperties: the first nXi elements are equal to Xi, and the last one is 1 - sum(Xi).
Full-state models: reducedX = false and nXi = nS. In this case, Xi = X, i.e., all the elements of the composition vector are considered as independent variables, and the constraint sum(X) = 1 is never written explicitly. Although this kind of model is heavier, as it provides one extra state variable, it can be less prone to numerical and/or symbolic problems, which can be caused by that constraint.
Fixed-composition models: fixedX = true and nXi = 0. In this case X = reference_X, i.e. all the elements of the composition vector are fixed.

The medium implementor can declare the value reducedX as final. In this way only one implementation must be given. For instance, Modelica.Media.IdealGases models declare final reducedX = false, so that the implementation can always assume nXi = nX. The same is true for Air.MoistAir, which declares final reducedX = true, and always assumes nXi = nX - 1 = 1.

It is also possible to leave reducedX modifiable. In this case, the BaseProperties model and all additional functions should check for the actual value of reducedX, and provide the corresponding implementation.

If fixedX is left modifiable, then the implementation should also handle the case fixedX = true properly.

Fluid connectors should always use composition vectors of size Xi, such as in the Modelica_Fluid library:

connector FluidPort
  replaceable package Medium = Modelica.Media.Interfaces.PartialMedium;
  Medium.AbsolutePressure      p;
  flow Medium.MassFlowRate     m_flow;

  Medium.SpecificEnthalpy      h;
  flow Medium.EnthalpyFlowRate H_flow;

  Medium.MassFraction          Xi    [Medium.nXi];
  flow Medium.MassFlowRate     mX_flow[Medium.nXi];
end FluidPort;

For further details, refer to the implementation of MixtureGasNasa model and MoistAir model.

Modelica.Media.UsersGuide.MediumDefinition.SpecificEnthalpyAsFunction

If pressure p and specific enthalpy h are not used as independent medium variables, the specific enthalpy should be computed by a Modelica function that has as input arguments only the independent medium variables. It should not be computed by an equation. For example, if p and T are used as independent medium variables, a function h_pT(p,T) should be defined that is called to compute h:

    h = h_pT(p,T);

The reason for this rule requires a longer explanation. In short, if h is not a computed by a Modelica function and this function is non-linear in the independent medium variables, then non-linear systems of equations will occur at every connection point, if the FluidPort connectors from the Modelica_Fluid library are used (these are the same as in Modelica.Media.Examples.Tests.Components.FluidPort). Only, if the above rule is fulfilled, a tool is able to remove these non-linear system of equations in most cases.

The basic idea of the FluidPort connector is that 2 or more components can be connected together at a point and that automatically the mass and energy balance is fulfilled in the connection point, i.e., the ideal mixing equations are generated. Note, the momentum balance is only correct for straight line connections. If "ideal mixing" is not sufficient, a special component to define the mixing equations must be introduced.

The mass and momentum balance equations in a component are derived from the partial differential equations along the flow direction of a pipe:

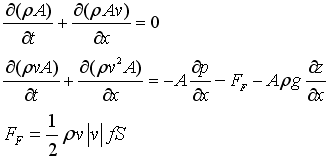
Note, F_F is the fanning friction factor. The energy balance can be given in different forms. Usually, it is given as:

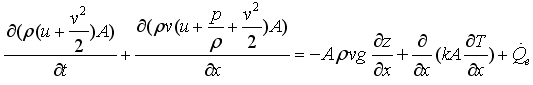
This form describes the change of the internal energy, kinetic energy and potential energy of a volume as function of the in and out flowing fluid. Multiplying the momentum balance with the flow velocity v and subtracting it from the energy balance above, results in the following alternative form of the energy balance:

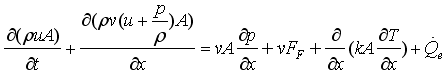
This form has the advantage that the kinetic and potential energy is no longer part of the energy balance and therefore the energy balance is substantially simpler (e.g., additional non-linear systems of equations occur in the first form since the velocity is present in the energy balance; in the second form this is not the case and it is still valid also for high speeds).

Assume now that the second form of the energy balance above is used in all components and that the following FluidPort connector is used in all components:

connector FluidPort
  replaceable package Medium = Modelica.Media.Interfaces.PartialMedium;
  Medium.AbsolutePressure      p;
  flow Medium.MassFlowRate     m_flow;

  Medium.SpecificEnthalpy      h;
  flow Medium.EnthalpyFlowRate H_flow;

  Medium.MassFraction          Xi    [Medium.nXi];
  flow Medium.MassFlowRate     mX_flow[Medium.nXi];
end FluidPort;

As an example, assume that 3 components are connected together and that the medium is a single substance fluid. This will result in the following connection equations:

    p1=p2=p3;
    h1=h2=h3;
    0 = m_flow1 + m_flow2 + m_flow3;
    0 = H_flow1 + H_flow2 + H_flow3;

These are the mass balance and the energy balance (form 2) of an infinitesimal volume in the connection point under the assumption that no mass or energy is stored in this volume. In other words, the connection equations are the equations that describe ideal mixing. Under the assumption that the velocity vectors of the 3 flows are identical (especially, they are parallel), also the momentum balance is fulfilled:

   0 = m_flow1*v1 + m_flow2*v2 + m_flow3*v3;
     = v*(m_flow1 + m_flow2 + m_flow3);
     = 0;

With the above connector it is therefore possible to connect components together in a nearly arbitrary fashion, because every connection fulfills automatically the balance equations. This approach has, however, one drawback: If two components are connected together, then the medium variables on both sides of the connector are identical. However, due to the connector, only the two equations

   p1 = p2;
   h1 = h2;

are present. Assume, that p,T are the independent medium variables and that the medium properties are computed at one side of the connections. This means, the following equations are basically present:

    h1 = h(p1,T1);
    h2 = h(p2,T2);
    p1 = p2;
    h1 = h2;

These equations can be solved in the following way:

    h1 := h(p1,T1)
    p2 := p1;
    h2 := h1;
    0  := h2 - h(p2,T2);   // non-linear system of equations for T2

This means that T2 is computed by solving a non-linear system of equations. If h1 and h2 are provided as Modelica functions, a Modelica translator, such as Dymola, can replace this non-linear system of equations by the equation:

   T2 := T1;

because after alias substition there are two function calls

    h1 := h(p1,T1);
    h1 := h(p1,T2);

Since the left hand side of the function call and the first argument are the same, the second arguments T1 and T2 must also be identical and therefore T2 := T1. This type of analysis seems to be only possible, if the specific enthalpy is defined as a function of the independent medium variables.

Modelica.Media.UsersGuide.MediumDefinition.StaticStateSelection

Without pre-caution when implementing a medium model, it is very easy that non-linear algebraic systems of equations occur when using the medium model. In this section it is explained how to avoid non-linear systems of equations that result from unnecessary dynamic state selections.

A medium model should be implemented in such a way that a tool is able to select states of a medium in a balance volume statically (during translation). This is only possible if the medium equations are written in a specific way. Otherwise, a tool has to dynamically select states during simulation. Since medium equations are usually non-linear, this means that non-linear algebraic systems of equations would occur in every balance volume.

It is assumed that medium equations in a balance volume are defined in the following way:

    package Medium = Modelica.Media.Interfaces.PartialMedium;
    Medium.BaseProperties medium;
  equation
     // mass balance
       der(M)  = port_a.m_flow + port_b.m_flow;
       der(MX) = port_a_mX_flow + port_b_mX_flow;
             M = V*medium.d;
            MX = M*medium.X;

     // Energy balance
     U = M*medium.u;
     der(U) = port_a.H_flow+port_b.H_flow;

Single Substance Media

A medium consisting of a single substance has to define two of "p,T,d,u,h" with stateSelect=StateSelect.prefer if BaseProperties.preferredMediumstates = true and has to provide the other three variables as function of these states. This results in:

static state selection (no dynamic choices).
a linear system of equations in the two state derivatives.

Example for a single substance medium

p, T are preferred states (i.e. StateSelect.prefer is set) and there are three equations written in the form:

   d = fd(p,T)
   u = fu(p,T)
   h = fh(p,T)

Index reduction leads to the equations:

   der(M) = V*der(d)
   der(U) = der(M)*u + M*der(u)
   der(d) = der(fd,p)*der(p) + der(fd,T)*der(T)
   der(u) = der(fu,p)*der(p) + der(fu,T)*der(T)

Note, that der(y,x) is the partial derivative of y with respect to x and that this operator will be introduced in a future version of the Modelica language. The above equations imply, that if p,T are provided from the integrator as states, all functions, such as fd(p,T) or der(fd,p) can be evaluated as function of the states. The overall system results in a linear system of equations in der(p) and der(T) after eliminating der(M), der(U), der(d), der(u) via tearing.

Counter Example for a single substance medium

An ideal gas with one substance is written in the form

  redeclare model extends BaseProperties(
     T(stateSelect=if preferredMediumStates then StateSelect.prefer else StateSelect.default),
     p(stateSelect=if preferredMediumStates then StateSelect.prefer else StateSelect.default)
  equation
     h = h(T);
     u = h - R*T;
     p = d*R*T;
      ...
  end BaseProperties;

If p, T are preferred states, these equations are not written in the recommended form, because d is not a function of p and T. If p,T would be states, it would be necessary to solve for the density:

   d = p/(R*T)

If T or R are zero, this results in a division by zero. A tool does not know that R or T cannot become zero. Therefore, a tool must assume that p, T cannot always be selected as states and has to either use another static state selection or use dynamic state selection. The only other choice for static state selection is d,T, because h,u,p are given as functions of d,T. However, as potential states only variables appearing differentiated and variables declared with StateSelect.prefer or StateSelect.always are used. Since "d" does not appear differentiated and has StateSelect.default, it cannot be selected as a state. As a result, the tool has to select states dynamically during simulation. Since the equations above are non-linear and they are utilized in the dynamic state selection, a non-linear system of equations is present in every balance volume.

To summarize, for single substance ideal gas media there are the following two possibilities to get static state selection and linear systems of equations:

Use p,T as preferred states and write the equation for d in the form: d = p/(T*R)
Use d,T as preferred states and write the equation for p in the form: p = d*T*R

All other settings (other/no preferred states etc.) lead to dynamic state selection and non-linear systems of equations for a balance volume.

Multiple Substance Media

A medium consisting of multiple substance has to define two of "p,T,d,u,h" as well as the mass fractions Xi with stateSelect=StateSelect.prefer (if BaseProperties.preferredMediumStates = true) and has to provide the other three variables as functions of these states. Only then, static selection is possible for a tool.

Example for a multiple substance medium:

p, T and Xi are defined as preferred states and the equations are written in the form:

   d = fp(p,T,Xi);
   u = fu(p,T,Xi);
   h = fh(p,T,Xi);

Since the balance equations are written in the form:

              M = V*medium.d;
            MXi = M*medium.Xi;

The variables M and MXi appearing differentiated in the balance equations are provided as functions of d and Xi and since d is given as a function of p, T and Xi, it is possible to compute M and MXi directly from the desired states. This means that static state selection is possible.

Modelica.Media.UsersGuide.MediumDefinition.TestOfMedium

After implementation of a new medium model, it should be tested. A basic test is already provided with model Modelica.Media.Examples.Tests.Components.PartialTestModel which might be used in the following way:

  model TestOfMyMedium
     extends Modelica.Media.Examples.Tests.Components.PartialTestModel(
              redeclare package Medium = MyMedium);
  end TestOfMyMedium;

It might be necessary to adapt or change initial values depending on the validity range of the medium. The model above should translate and simulate. If the medium model is written according to the suggestions given in the previous sections (and the Modelica translator has appropriate algorithms implemented), there should be only static state selection everywhere and no non-linear system of equations, provided h is an independent medium variable or is only a function of T. If h is a function of, say h=h(p,T), one non-linear system of equations occurs that cannot be avoided.

The test model above can be used to test the most basic properties. Of course, more tests should be performed.

HTML-documentation generated by Dymola Sun Jan 17 21:12:17 2010.