Modelica.Blocks.Nonlinear

Information

This package contains discontinuous and non-differentiable, algebraic input/output blocks.

Extends from Modelica.Icons.Library (Icon for library).

Package Content

Name	Description
Limiter	Limit the range of a signal
VariableLimiter	Limit the range of a signal with variable limits
DeadZone	Provide a region of zero output
FixedDelay	Delay block with fixed DelayTime
PadeDelay	Pade approximation of delay block with fixed DelayTime
VariableDelay	Delay block with variable DelayTime

Modelica.Blocks.Nonlinear.Limiter

Information

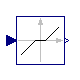
The Limiter block passes its input signal as output signal as long as the input is within the specified upper and lower limits. If this is not the case, the corresponding limits are passed as output.

Extends from Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Type	Name	Default	Description
Real	uMax		Upper limits of input signals
Real	uMin	-uMax	Lower limits of input signals
Boolean	limitsAtInit	true	= false, if limits are ignored during initializiation (i.e., y=u)

Connectors

Type	Name	Description
input RealInput	u	Connector of Real input signal
output RealOutput	y	Connector of Real output signal

Modelica definition

block Limiter "Limit the range of a signal"
  parameter Real uMax(start=1) "Upper limits of input signals";
  parameter Real uMin= -uMax "Lower limits of input signals";
  parameter Boolean limitsAtInit = true 
    "= false, if limits are ignored during initializiation (i.e., y=u)";
  extends Interfaces.SISO;

equation 
  assert(uMax >= uMin, "Limiter: Limits must be consistent. However, uMax (=" + String(uMax) +
                       ") < uMin (=" + String(uMin) + ")");
  if initial() and not limitsAtInit then
     y = u;
     assert(u >= uMin - 0.01*abs(uMin) and 
            u <= uMax + 0.01*abs(uMax),
           "Limiter: During initialization the limits have been ignored.\n"+
           "However, the result is that the input u is not within the required limits:\n"+
           "  u = " + String(u) + ", uMin = " + String(uMin) + ", uMax = " + String(uMax));
  else
     y = smooth(0,if u > uMax then uMax else if u < uMin then uMin else u);
  end if;
end Limiter;

Modelica.Blocks.Nonlinear.VariableLimiter

Information

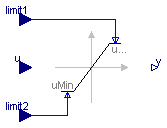
The Limiter block passes its input signal as output signal as long as the input is within the upper and lower limits specified by the two additional inputs limit1 and limit2. If this is not the case, the corresponding limit is passed as output.

Extends from Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Type	Name	Default	Description
Boolean	limitsAtInit	true	= false, if limits are ignored during initializiation (i.e., y=u)

Connectors

Type	Name	Description
input RealInput	u	Connector of Real input signal
output RealOutput	y	Connector of Real output signal
input RealInput	limit1	Connector of Real input signal used as maximum of input u
input RealInput	limit2	Connector of Real input signal used as minimum of input u

Modelica definition

block VariableLimiter 
  "Limit the range of a signal with variable limits"
  extends Interfaces.SISO;
  parameter Boolean limitsAtInit = true 
    "= false, if limits are ignored during initializiation (i.e., y=u)";
  Interfaces.RealInput limit1 
    "Connector of Real input signal used as maximum of input u";
  Interfaces.RealInput limit2 
    "Connector of Real input signal used as minimum of input u";
protected 
  Real uMax;
  Real uMin;

equation 
  uMax = max(limit1, limit2);
  uMin = min(limit1, limit2);

  if initial() and not limitsAtInit then
     y = u;
     assert(u >= uMin - 0.01*abs(uMin) and 
            u <= uMax + 0.01*abs(uMax),
           "VariableLimiter: During initialization the limits have been ignored.\n"+
           "However, the result is that the input u is not within the required limits:\n"+
           "  u = " + String(u) + ", uMin = " + String(uMin) + ", uMax = " + String(uMax));
  else
     y = smooth(0,if u > uMax then uMax else if u < uMin then uMin else u);
  end if;
end VariableLimiter;

Modelica.Blocks.Nonlinear.DeadZone

Information

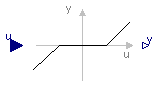
The DeadZone block defines a region of zero output.

If the input is within uMin ... uMax, the output is zero. Outside of this zone, the output is a linear function of the input with a slope of 1.

Extends from Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Type	Name	Default	Description
Real	uMax		Upper limits of dead zones
Real	uMin	-uMax	Lower limits of dead zones
Boolean	deadZoneAtInit	true	= false, if dead zone is ignored during initializiation (i.e., y=u)

Connectors

Type	Name	Description
input RealInput	u	Connector of Real input signal
output RealOutput	y	Connector of Real output signal

Modelica definition

block DeadZone "Provide a region of zero output"
  parameter Real uMax(start=1) "Upper limits of dead zones";
  parameter Real uMin=-uMax "Lower limits of dead zones";
  parameter Boolean deadZoneAtInit = true 
    "= false, if dead zone is ignored during initializiation (i.e., y=u)";
  extends Interfaces.SISO;

equation 
  assert(uMax >= uMin, "DeadZone: Limits must be consistent. However, uMax (=" + String(uMax) +
                       ") < uMin (=" + String(uMin) + ")");

  if initial() and not deadZoneAtInit then
     y = u;
  else
     y = smooth(0,if u > uMax then u - uMax else if u < uMin then u - uMin else 0);
  end if;
end DeadZone;

Modelica.Blocks.Nonlinear.FixedDelay

Information

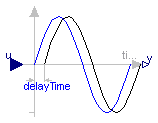
The Input signal is delayed by a given time instant, or more precisely:

   y = u(time - delayTime) for time > time.start + delayTime
     = u(time.start)       for time ≤ time.start + delayTime

Extends from Modelica.Blocks.Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Type	Name	Default	Description
Time	delayTime		Delay time of output with respect to input signal [s]

Connectors

Type	Name	Description
input RealInput	u	Connector of Real input signal
output RealOutput	y	Connector of Real output signal

Modelica definition

block FixedDelay "Delay block with fixed DelayTime"
  extends Modelica.Blocks.Interfaces.SISO;
  parameter SI.Time delayTime(start=1) 
    "Delay time of output with respect to input signal";

equation 
  y = delay(u, delayTime);
end FixedDelay;

Modelica.Blocks.Nonlinear.PadeDelay

Information

The Input signal is delayed by a given time instant, or more precisely:

   y = u(time - delayTime) for time > time.start + delayTime
     = u(time.start)       for time ≤ time.start + delayTime

The delay is approximated by a Pade approximation, i.e., by a transfer function

           b[1]*s^m + b[2]*s^[m-1] + ... + b[m+1]
   y(s) = --------------------------------------------- * u(s)
           a[1]*s^n + a[2]*s^[n-1] + ... + a[n+1]

where the coefficients b[:] and a[:] are calculated such that the coefficients of the Taylor expansion of the delay exp(-T*s) around s=0 are identical upto order n+m.

The main advantage of this approach is that the delay is approximated by a linear differential equation system, which is continuous and continuously differentiable. For example, it is uncritical to linearize a system containing a Pade-approximated delay.

The standard text book version uses order "m=n", which is also the default setting of this block. The setting "m=n-1" may yield a better approximation in certain cases.

Literature:
Otto Foellinger: Regelungstechnik, 8. Auflage, chapter 11.9, page 412-414, Huethig Verlag Heidelberg, 1994

Extends from Modelica.Blocks.Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Type	Name	Default	Description
Time	delayTime		Delay time of output with respect to input signal [s]
Integer	n	1	Order of pade approximation
Integer	m	n	Order of numerator

Connectors

Type	Name	Description
input RealInput	u	Connector of Real input signal
output RealOutput	y	Connector of Real output signal

Modelica definition

block PadeDelay 
  "Pade approximation of delay block with fixed DelayTime "
  extends Modelica.Blocks.Interfaces.SISO;
  parameter SI.Time delayTime(start=1) 
    "Delay time of output with respect to input signal";
  parameter Integer n(min=1) = 1 "Order of pade approximation";
  parameter Integer m(
    min=1,
    max=n) = n "Order of numerator";

protected 
  Real x1dot "Derivative of first state of TransferFcn";
  Real xn "Highest order state of TransferFcn";
  Real a[n + 1];
  Real b[m + 1];

public 
  final output Real x[n] 
    "State of transfer function from controller canonical form";

protected 
  function padeCoefficients
    input Real T "delay time";
    input Integer n "order of denominator";
    input Integer m "order of numerator";
    output Real b[m + 1] "numerator coefficients of transfer function";
    output Real a[n + 1] "denominator coefficients of transfer function";
  protected 
    Real nm;
  algorithm 
    a[1] := 1;
    b[1] := 1;
    nm := n + m;

    for i in 1:n loop
      a[i + 1] := a[i]*(T*((n - i + 1)/(nm - i + 1))/i);
      if i <= m then
        b[i + 1] := -b[i]*(T*((m - i + 1)/(nm - i + 1))/i);
      end if;
    end for;

    b := b[m + 1:-1:1];
    a := a[n + 1:-1:1];
  end padeCoefficients;
equation 

  (b,a) = padeCoefficients(delayTime, n, m);

  [der(x); xn] = [x1dot; x];
  [u] = transpose([a])*[x1dot; x];
  [y] = transpose([zeros(n - m, 1); b])*[x1dot; x];

initial equation 
  x[n] = u;
end PadeDelay;

Modelica.Blocks.Nonlinear.VariableDelay

Information

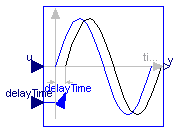
The Input signal is delayed by a given time instant, or more precisely:

   y = u(time - delayTime) for time > time.start + delayTime
     = u(time.start)       for time ≤ time.start + delayTime

where delayTime is an additional input signal which must follow the following relationship:

  0 ≤ delayTime ≤ delayMax

Extends from Modelica.Blocks.Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Type	Name	Default	Description
Real	delayMax		maximum delay time

Connectors

Type	Name	Description
input RealInput	u	Connector of Real input signal
output RealOutput	y	Connector of Real output signal
input RealInput	delayTime

Modelica definition

block VariableDelay "Delay block with variable DelayTime"
  extends Modelica.Blocks.Interfaces.SISO;
  parameter Real delayMax(min=0, start=1) "maximum delay time";

  Modelica.Blocks.Interfaces.RealInput delayTime;
equation 
  y = delay(u, delayTime, delayMax);
end VariableDelay;