Modelica.Blocks.Discrete

Information

This package contains discrete control blocks with fixed sample period. Every component of this package is structured in the following way:

1. A component has continuous real input and output signals.
2. The input signals are sampled by the given sample period defined via parameter samplePeriod. The first sample instant is defined by parameter startTime.
3. The output signals are computed from the sampled input signals.

A sampled data system may consist of components of package Discrete and of every other purely algebraic input/output block, such as the components of packages Modelica.Blocks.Math, Modelica.Blocks.Nonlinear or Modelica.Blocks.Sources.

Extends from Modelica.Icons.Library (Icon for library).

Package Content

Name	Description
Sampler	Ideal sampling of continuous signals
ZeroOrderHold	Zero order hold of a sampled-data system
FirstOrderHold	First order hold of a sampled-data system
UnitDelay	Unit Delay Block
TransferFunction	Discrete Transfer Function block
StateSpace	Discrete State Space block
TriggeredSampler	Triggered sampling of continuous signals
TriggeredMax	Compute maximum, absolute value of continuous signal at trigger instants

Modelica.Blocks.Discrete.Sampler

Information

Samples the continues input signal with a sampling rate defined via parameter samplePeriod.

Extends from Interfaces.DiscreteSISO (Single Input Single Output discrete control block).

Parameters

Type	Name	Default	Description
Time	samplePeriod		Sample period of component [s]
Time	startTime	0	First sample time instant [s]

Connectors

Type	Name	Description
input RealInput	u	Continuous input signal
output RealOutput	y	Continuous output signal

Modelica definition

block Sampler "Ideal sampling of continuous signals"
  extends Interfaces.DiscreteSISO;

equation 
  when {sampleTrigger, initial()} then
    y = u;
  end when;
end Sampler;

Modelica.Blocks.Discrete.ZeroOrderHold

Information

The output is identical to the sampled input signal at sample time instants and holds the output at the value of the last sample instant during the sample points.

Extends from Interfaces.DiscreteSISO (Single Input Single Output discrete control block).

Parameters

Type	Name	Default	Description
Time	samplePeriod		Sample period of component [s]
Time	startTime	0	First sample time instant [s]

Connectors

Type	Name	Description
input RealInput	u	Continuous input signal
output RealOutput	y	Continuous output signal

Modelica definition

block ZeroOrderHold "Zero order hold of a sampled-data system"
  extends Interfaces.DiscreteSISO;
  output Real ySample(start=0, fixed=true);

equation 
  when {sampleTrigger, initial()} then
    ySample = u;
  end when;
  /* Define y=ySample with an infinitesimal delay to break potential
       algebraic loops if both the continuous and the discrete part have
       direct feedthrough
    */
  y = pre(ySample);
end ZeroOrderHold;

Modelica.Blocks.Discrete.FirstOrderHold

Information

The output signal is the extrapolation through the values of the last two sampled input signals.

Extends from Interfaces.DiscreteSISO (Single Input Single Output discrete control block).

Parameters

Type	Name	Default	Description
Time	samplePeriod		Sample period of component [s]
Time	startTime	0	First sample time instant [s]

Connectors

Type	Name	Description
input RealInput	u	Continuous input signal
output RealOutput	y	Continuous output signal

Modelica definition

block FirstOrderHold "First order hold of a sampled-data system"
  extends Interfaces.DiscreteSISO;
protected 
  Real ySample;
  Modelica.SIunits.Time tSample;
  Real c;

equation 
  when sampleTrigger then
    ySample = u;
    tSample = time;
    c = if firstTrigger then 0 else (ySample - pre(ySample))/samplePeriod;
  end when;
  /* Use pre(ySample) and pre(c) to break potential algebraic loops by an
       infinitesimal delay if both the continuous and the discrete part
       have direct feedthrough.
    */
  y = pre(ySample) + pre(c)*(time - tSample);
end FirstOrderHold;

Modelica.Blocks.Discrete.UnitDelay

Information

This block describes a unit delay:

          1
     y = --- * u
          z

that is, the output signal y is the input signal u of the previous sample instant. Before the second sample instant, the output y is identical to parameter yStart.

Extends from Interfaces.DiscreteSISO (Single Input Single Output discrete control block).

Parameters

Type	Name	Default	Description
Real	y_start	0	Initial value of output signal
Time	samplePeriod		Sample period of component [s]
Time	startTime	0	First sample time instant [s]

Connectors

Type	Name	Description
input RealInput	u	Continuous input signal
output RealOutput	y	Continuous output signal

Modelica definition

block UnitDelay "Unit Delay Block"
  parameter Real y_start=0 "Initial value of output signal";
  extends Interfaces.DiscreteSISO;

equation 
  when sampleTrigger then
    y = pre(u);
  end when;

initial equation 
    y = y_start;
end UnitDelay;

Modelica.Blocks.Discrete.TransferFunction

Information

The discrete transfer function block defines the transfer function between the input signal u and the output signal y. The numerator has the order nb-1, the denominator has the order na-1.

          b(1)*z^(nb-1) + b(2)*z^(nb-2) + ... + b(nb)
   y(z) = -------------------------------------------- * u(z)
          a(1)*z^(na-1) + a(2)*z^(na-2) + ... + a(na)

State variables x are defined according to controller canonical form. Initial values of the states can be set as start values of x.

Example:

     Blocks.Discrete.TransferFunction g(b = {2,4}, a = {1,3});

results in the following transfer function:

        2*z + 4
   y = --------- * u
         z + 3

Extends from Interfaces.DiscreteSISO (Single Input Single Output discrete control block).

Parameters

Type	Name	Default	Description
Real	b[:]	{1}	Numerator coefficients of transfer function.
Real	a[:]		Denominator coefficients of transfer function.
Time	samplePeriod		Sample period of component [s]
Time	startTime	0	First sample time instant [s]

Connectors

Type	Name	Description
input RealInput	u	Continuous input signal
output RealOutput	y	Continuous output signal

Modelica definition

block TransferFunction "Discrete Transfer Function block"
  parameter Real b[:]={1} "Numerator coefficients of transfer function.";
  parameter Real a[:] "Denominator coefficients of transfer function.";
  extends Interfaces.DiscreteSISO;
  output Real x[size(a, 1) - 1](each start=0, each fixed=true) 
    "State of transfer function from controller canonical form";
protected 
  parameter Integer nb=size(b, 1) "Size of Numerator of transfer function";
  parameter Integer na=size(a, 1) "Size of Denominator of transfer function";
  Real x1;
  Real xext[size(a, 1)];

equation 
  when sampleTrigger then
    /* State variables x are defined according to
       controller canonical form. */
    x1 = (u - a[2:size(a, 1)]*pre(x))/a[1];
    xext = vector([x1; pre(x)]);
    x = xext[1:size(x, 1)];
    y = vector([zeros(na - nb, 1); b])*xext;
  end when;
  /* This is a non-sampled equation and above there are two separate
       when-clauses. This breaks feeback loops without direct terms,
       since in that case y will be independent of x1 (and only dependent
       on pre(x)).
    */
  /* Corresponding (simpler) version using when-semantics of Modelica 1.3:
   equation
     when sampleTrigger then
      [x; xn] = [x1; pre(x)];
      [u] = transpose([a])*[x1; pre(x)];
      [y] = transpose([zeros(na - nb, 1); b])*[x1; pre(x)];
     end when;
*/
end TransferFunction;

Modelica.Blocks.Discrete.StateSpace

Information

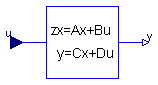
The discrete state space block defines the relation between the input u=inPort.signal and the output y=outPort.signal in state space form:

    x = A * pre(x) + B * u
    y = C * pre(x) + D * u

where pre(x) is the value of the discrete state x at the previous sample time instant. The input is a vector of length nu, the output is a vector of length ny and nx is the number of states. Accordingly

        A has the dimension: A(nx,nx),
        B has the dimension: B(nx,nu),
        C has the dimension: C(ny,nx),
        D has the dimension: D(ny,nu)

Example:

     parameter: A = [0.12, 2;3, 1.5]
     parameter: B = [2, 7;3, 1]
     parameter: C = [0.1, 2]
     parameter: D = zeros(ny,nu)

results in the following equations:
  [x[1]]   [0.12  2.00] [pre(x[1])]   [2.0  7.0] [u[1]]
  [    ] = [          ]*[         ] + [        ]*[    ]
  [x[2]]   [3.00  1.50] [pre(x[2])]   [0.1  2.0] [u[2]]
                             [pre(x[1])]            [u[1]]
       y[1]   = [0.1  2.0] * [         ] + [0  0] * [    ]
                             [pre(x[2])]            [u[2]]

Extends from Interfaces.DiscreteMIMO (Multiple Input Multiple Output discrete control block).

Parameters

Type	Name	Default	Description
Real	A[:, size(A, 1)]		Matrix A of state space model
Real	B[size(A, 1), :]		Matrix B of state space model
Real	C[:, size(A, 1)]		Matrix C of state space model
Real	D[size(C, 1), size(B, 2)]	zeros(size(C, 1), size(B, 2))	Matrix D of state space model
Time	samplePeriod		Sample period of component [s]
Time	startTime	0	First sample time instant [s]
Integer	nin	size(B, 2)	Number of inputs
Integer	nout	size(C, 1)	Number of outputs

Connectors

Type	Name	Description
input RealInput	u[nin]	Continuous input signals
output RealOutput	y[nout]	Continuous output signals

Modelica definition

block StateSpace "Discrete State Space block"
  parameter Real A[:, size(A, 1)] "Matrix A of state space model";
  parameter Real B[size(A, 1), :] "Matrix B of state space model";
  parameter Real C[:, size(A, 1)] "Matrix C of state space model";
  parameter Real D[size(C, 1), size(B, 2)]=zeros(size(C, 1), size(B, 2)) 
    "Matrix D of state space model";

  extends Interfaces.DiscreteMIMO(final nin=size(B, 2), final nout=size(C, 1));
  output Real x[size(A, 1)] "State vector";

equation 
  when sampleTrigger then
    x = A*pre(x) + B*u;
    y = C*pre(x) + D*u;
  end when;
end StateSpace;

Modelica.Blocks.Discrete.TriggeredSampler

Information

Samples the continuous input signal whenever the trigger input signal is rising (i.e., trigger changes from false to true) and provides the sampled input signal as output. Before the first sampling, the output signal is equal to the initial value defined via parameter y0.

Extends from Interfaces.DiscreteBlockIcon (Graphical layout of discrete block component icon).

Parameters

Type	Name	Default	Description
Real	y_start	0	initial value of output signal

Connectors

Type	Name	Description
input RealInput	u	Connector with a Real input signal
output RealOutput	y	Connector with a Real output signal
input BooleanInput	trigger

Modelica definition

block TriggeredSampler "Triggered sampling of continuous signals"
  extends Interfaces.DiscreteBlockIcon;
  parameter Real y_start=0 "initial value of output signal";

  Modelica.Blocks.Interfaces.RealInput u "Connector with a Real input signal";
  Modelica.Blocks.Interfaces.RealOutput y "Connector with a Real output signal";
  Modelica.Blocks.Interfaces.BooleanInput trigger;
equation 
  when trigger then
    y = u;
  end when;
initial equation 
  y = y_start;
end TriggeredSampler;

Modelica.Blocks.Discrete.TriggeredMax

Information

Samples the continuous input signal whenever the trigger input signal is rising (i.e., trigger changes from false to true). The maximum, absolute value of the input signal at the sampling point is provided as output signal.

Extends from Interfaces.DiscreteBlockIcon (Graphical layout of discrete block component icon).

Connectors

Type	Name	Description
input RealInput	u	Connector with a Real input signal
output RealOutput	y	Connector with a Real output signal
input BooleanInput	trigger

Modelica definition

block TriggeredMax 
  "Compute maximum, absolute value of continuous signal at trigger instants"

  extends Interfaces.DiscreteBlockIcon;
  Modelica.Blocks.Interfaces.RealInput u "Connector with a Real input signal";
  Modelica.Blocks.Interfaces.RealOutput y "Connector with a Real output signal";
  Modelica.Blocks.Interfaces.BooleanInput trigger;
equation 
  when trigger then
     y = max(pre(y), abs(u));
  end when;
initial equation 
  y = 0;
end TriggeredMax;