Buildings.Fluid.HeatExchangers.RadiantSlabs.UsersGuide
User's Guide
Information
Heat transfer through the slab
The figure below shows the thermal resistance network of the model for an example in which the pipes are embedded in the concrete slab, and the layers below the pipes are insulation and reinforced concrete.
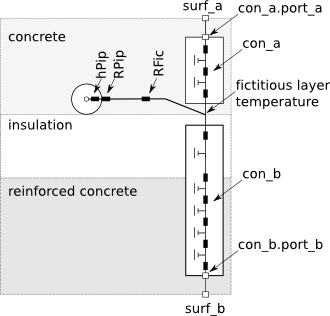
The construction con_a computes transient heat conduction
between the surface heat port surf_a and the
plane that contains the pipes, with the heat port con_a.port_a connecting to surf_a.
Similarly, the construction con_b is between the plane
that contains the pipes and the surface heat port
sur_b, with the heat port con_b.port_b connecting to surf_b.
The temperature of the plane that contains the pipes is computes using a fictitious
resistance RFic, which is computed by
Buildings.Fluid.HeatExchangers.RadiantSlabs.BaseClasses.Functions.AverageResistance.
There is also a resistance for the pipe wall RPip
and a convective heat transfer coefficient between the fluid and the pipe inside wall.
The convective heat transfer coefficient is a function of the mass flow rate and is computed
in
Buildings.Fluid.HeatExchangers.RadiantSlabs.BaseClasses.PipeToSlabConductance.
Material layers
The material layers are declared by the parameter layers, which is an instance of
Buildings.HeatTransfer.Data.OpaqueConstructions.
The first layer of this material is the one at the heat port surf_a, and the last layer
is at the heat port surf_b.
The parameter iLayPip must be set to the number of the interface in which the pipes
are located. For example, consider the following floor slab.
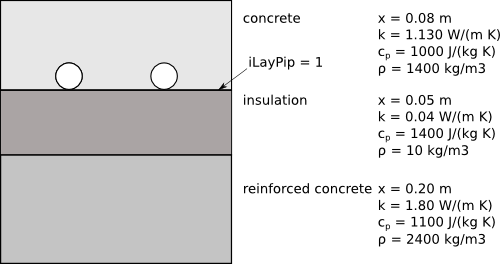
Buildings.HeatTransfer.Data.OpaqueConstructions.Generic layers(
nLay=3,
material={
Buildings.HeatTransfer.Data.Solids.Generic(
x=0.08,
k=1.13,
c=1000,
d=1400,
nSta=5),
Buildings.HeatTransfer.Data.Solids.Generic(
x=0.05,
k=0.04,
c=1400,
d=10),
Buildings.HeatTransfer.Data.Solids.Generic(
x=0.2,
k=1.8,
c=1100,
d=2400)}) "Material definition for floor construction";
Note that we set nSta=5 in the first material layer. In this example,
this material layer is the concrete layer in which the pipes are embedded. By setting
nSta=5 the simulation is forced to be done with five state variables in this layer.
The default setting would have led to only one state variable in this layer.
Since the pipes are at the interface of the concrete and the insulation,
we set iLayPip=1.
Discretization along the flow path
If the parameter heatTransfer=EpsilonNTU, then the heat transfer between the fluid
and the fictitious layer temperature is computed using an ε-NTU model.
If heatTransfer=FiniteDifference, then the pipe and the slab is
discretized along the water flow direction and a finite difference model is used
to compute the heat transfer. The parameter nSeg determines
how many times the resistance network is instantiated along the flow path.
However, all instances connect to the same surface temperature heat ports
surf_a and surf_b.
The default value for is nSeg=1 if heatTransfer=EpsilonNTU
and nSeg=5 if heatTransfer=FiniteDifference.
For a typical building simulation, we recommend to use the default settings of
heatTransfer=EpsilonNTU and nSeg=1, as these lead to
fastest computing time.
However, for feedback control design in which the outlet temperature of the slab
is used, one may want to use heatTransfer=FiniteDifference and nSeg=5.
This will cause the model to use 5 parallel segments in which heat is conducted between the
control volume of the pipe fluid and the surfaces of the slab.
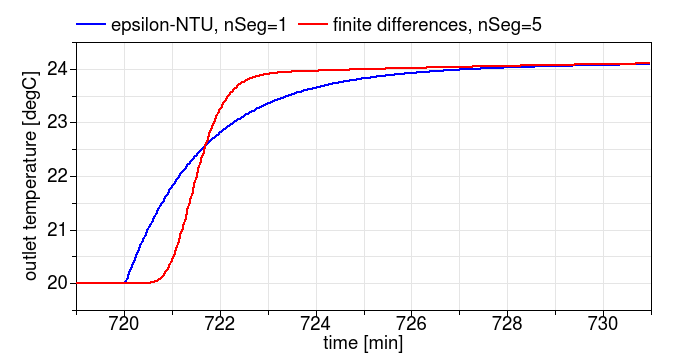
While the heat flow rate at the surface does not change noticeably between these
two configurations, the dynamics of
the water outlet temperature from the slab is significantly different. The
figure below shows the water outlet temperature response to a step change in the
volume flow rate at t=720 minutes. One can see that if
heatTransfer=EpsilonNTU and nSeg=1,
the response looks like a first order response (because nSeg=1),
while with heatTransfer=FiniteDifference and nSeg=5,
the response is higher order. This figure was generated using
Buildings.Fluid.HeatExchangers.RadiantSlabs.Examples.StepResponseFiniteDifference and
Buildings.Fluid.HeatExchangers.RadiantSlabs.Examples.StepResponseEpsilonNTU\.
Initialization
The initialization of the fluid in the pipes and of the slab temperature are independent of each other.
To initialize the medium, the same mechanism is used as for any other fluid
volume, such as
Buildings.Fluid.MixingVolumes.MixingVolume. Specifically,
the parameters
energyDynamics and massDynamics on the
Dynamics tab are used.
Depending on the values of these parameters, the medium is initialized using the values
p_start,
T_start,
X_start and
C_start, provided that the medium model contains
species concentrations X and trace substances C.
To initialize the construction temperatures, the parameters
steadyStateInitial,
T_a_start,
T_b_start and
T_c_start are used.
By default, T_c_start is set to the temperature that leads to steady-state
heat transfer between the surfaces surf_a and surf_b, whose
temperatures are both set to
T_a_start and
T_b_start.
The parameter pipe, which is an instance of the record
Buildings.Fluid.Data.Pipes,
defines the pipe material and geometry.
The parameter disPip declares the spacing between the pipes and
the parameter length, with default length=A/disPip
where A is the slab surface area,
declares the whole length of the pipe circuit.
The parameter sysTyp is used to select the equation that is used to compute
the average temperature in the plane of the pipes.
It needs to be set to the following values:
| sysTyp | System type |
|---|---|
| BaseClasses.Types.SystemType.Floor | Radiant heating or cooling systems with pipes embedded in the concrete slab above the thermal insulation. |
| BaseClasses.Types.SystemType.Ceiling_Wall_or_Capillary | Radiant heating or cooling systems with pipes embedded in the concrete slab in the ceiling, or radiant wall systems. Radiant heating and cooling systems with capillary heat exchanger at the construction surface. |
Limitations
The analogy with a three-resistance network and the corresponding equation for
Rx is based on a steady-state heat transfer analysis. Therefore, it is
only valid during steady-state.
For a fully dynamic model, a three-dimensional finite element method for the radiant slab would need to be implemented.
Implementation
To separate the material declaration layers into layers between the pipes
and heat port surf_a, and between the pipes and surf_b, the
vector layers.material[nLay] is partitioned into
layers.material[1:iLayPip] and layers.material[iLayPip+1:nLay].
The respective partitions are then assigned to the models for heat conduction between the
plane with the pipes and the construction surfaces, con_a and con_b.
Extends from Modelica.Icons.Information (Icon for general information packages).
