Buildings.Fluid.Movers.UsersGuide

This package contains models for fans and pumps. The same models are used for fans or pumps.

Model description

The models use performance curves that compute pressure rise, electrical power draw and efficiency as a function of the volume flow rate and the speed. These performance curves are described in Buildings.Fluid.Movers.BaseClasses.Characteristics.

Models that use performance curves for pressure rise

The models Buildings.Fluid.Movers.FlowMachine_y and Buildings.Fluid.Movers.FlowMachine_Nrpm take as an input either a control signal between 0 and 1, or the rotational speed in units of [1/min]. From this input and the current flow rate, they compute the pressure rise. This pressure rise is computed using user-provided list of operating points that defines the fan or pump curve at full speed. For other speeds, similarity laws are used to scale the performance curves, as described in Buildings.Fluid.Movers.BaseClasses.Characteristics.pressure.

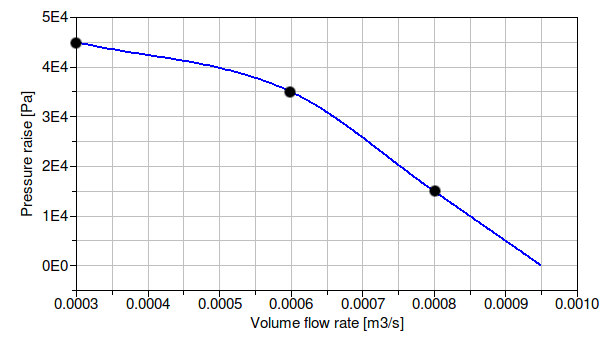
For example, suppose a pump needs to be modeled whose pressure versus flow relation crosses, at full speed, the points shown in the table below.

Volume flow rate [m3⁄h]	Head [Pa]
0.0003	45000
0.0006	35000
0.0008	15000

Then, a declaration would be

  Buildings.Fluid.Movers.FlowMachine_y pum(
    redeclare package Medium = Medium,
    pressure(V_flow={0.0003,0.0006,0.0008},
             dp    ={45,35,15}*1000))
    "Circulation pump";

This will model the following pump curve for the pump input signal y=1.

Models that have idealized perfect controls

The models Buildings.Fluid.Movers.FlowMachine_dp and Buildings.Fluid.Movers.FlowMachine_m_flow take as an input the pressure difference or the mass flow rate. This pressure difference or mass flow rate will be provided by the fan or pump, i.e., the fan or pump has idealized perfect control and infinite capacity. These two models do not have a performance curve for the flow characteristics. The reason for not using a performance curve for the flow characteristics is that

• for given pressure rise (or mass flow rate), the mass flow rate (or pressure rise) is defined by the flow resistance of the duct or piping network, and
• at zero pressure difference, solving for the flow rate and the revolution leads to a singularity.

Start-up and shut-down transients

All models have a parameter filteredSpeed. This parameter affects the fan output as follows:

1. If filteredSpeed=false, then the input signal y (or Nrpm, m_flow_in, or dp_in) is equal to the fan speed (or the mass flow rate or pressure rise). Thus, a step change in the input signal causes a step change in the fan speed (or mass flow rate or pressure rise).
2. If filteredSpeed=false, which is the default, then the fan speed (or the mass flow rate or the pressure rise) is equal to the output of a filter. This filter is implemented as a 2nd order differential equation and can be thought of as approximating the inertia of the rotor and the fluid. Thus, a step change in the fan input signal will cause a gradual change in the fan speed. The filter has a parameter riseTime, which by default is set to 30 seconds. The rise time is the time required to reach 99.6% of the full speed, or, if the fan is switched off, to reach a fan speed of 0.4%.

The figure below shows for a fan with filteredSpeed=true and riseTime=30 seconds the speed input signal and the actual speed.

Although many simulations do not require such a detailed model that approximates the transients of fans or pumps, it turns out that using this filter can reduce computing time and can lead to fewer convergence problems in large system models. With a filter, any sudden change in control signal, such as when a fan switches on, is damped before it affects the air flow rate. This continuous change in flow rate turns out to be easier, and in some cases faster, to simulate compared to a step change. For most simulations, we therefore recommend to use the default settings of filteredSpeed=true and riseTime=30 seconds. An exception are situations in which the fan or pump is operated at a fixed speed during the whole simulation. In this case, set filteredSpeed=false.

Note that if the fan is part of a closed loop control, then the filter affects the transient response of the control. When changing the value of filteredSpeed, the control gains may need to be retuned. We now present values control parameters that seem to work in most cases. Suppose there is a closed loop control with a PI-controller Buildings.Controls.Continuous.LimPID and a fan or pump, configured with filteredOpening=true and riseTime=30 seconds. Assume that the transient response of the other dynamic elements in the control loop is fast compared to the rise time of the filter. Then, a proportional gain of k=0.5 and an integrator time constant of Ti=15 seconds often yields satisfactory closed loop control performance. These values may need to be changed for different applications as they are also a function of the loop gain. If the control loop shows oscillatory behavior, then reduce k and/or increase Ti. If the control loop reacts too slow, do the opposite.

Efficiency and electrical power consumption

All models compute the motor power draw P_ele, the hydraulic power input W_hyd, the flow work W_flo and the heat dissipated into the medium Q. Based on the first law, the flow work is

W_flo = | V Δp |.

The heat dissipated into the medium is as follows: If the motor is cooled by the fluid, as indicated by motorCooledByFluid=true, then the heat dissipated into the medium is

Q = P_ele - W_flo.

If motorCooledByFluid=false, then the motor is outside the fluid stream, and only the shaft, or hydraulic, work W_hyd enters the thermodynamic control volume. Hence,

Q = Q_hyd - W_flo.

The efficiencies are computed as

η = W_flo ⁄ P_ele = η_hyd   η_mot
η_hyd = W_flo ⁄ W_hyd
η_mot = W_hyd ⁄ P_ele

where η_hyd is the hydraulic efficiency, η_mot is the motor efficiency and Q is the heat released by the motor.

If use_powerCharacteristic=true, then a set of data points for the power P_ele for different volume flow rates at full speed needs to be provided by the user. Using the flow work W_flo and the electrical power input P_ele, the total efficiency is computed as

η = W_flo ⁄ P_ele,

√η_hyd = √η_mot = η.

η = η_hyd   η_mot
P_ele = W_flo ⁄ η.

The efficiency data for the motor are a list of points r_V and η_mot, where r_V is the ratio of actual volume flow rate divided by the maximum volume flow rate V_flow_max, which is the volume flow rate at full speed and zero pressure rise. The maximum flow rate V_flow_max is obtained as follows: The models Buildings.Fluid.Movers.FlowMachine_y and Buildings.Fluid.Movers.FlowMachine_Nrpm set

  V_flow_max = V_flow(dp=0, r_N=1);

where r_N is the ratio of actual to nominal speed. Since Buildings.Fluid.Movers.FlowMachine_dp and Buildings.Fluid.Movers.FlowMachine_m_flow do not have a flow versus pressure performance curve, the parameter V_flow_max is assigned in these two models as

  V_flow_max = m_flow_nominal/rho_nominal,

where m_flow_nominal is the maximum flow rate, which needs to be provided by the user as a parameter for these models, and rho_nominal is the density at the nominal operating point.

Fluid volume of the component

All models can be configured to have a fluid volume at the low-pressure side. Adding such a volume sometimes helps the solver to find a solution during initialization and time integration of large models.

Enthalpy change of the component

If motorCooledByFluid=true, then the enthalpy change between the inlet and outlet fluid port is equal to the electrical power P_ele that is consumed by the component. Otherwise, it is equal to the hydraulic work W_hyd. The parameter addPowerToMedium, which is by default set to true, can be used to simplify the equations. If it is set to false, then no enthalpy change occurs between inlet and outlet other than the flow work W_flo. This can lead to simpler equations, but the temperature rise across the component will be underestimated, in particular for fans.

Further description

For a detailed description of the models with names FlowMachine_*, see their base class Buildings.Fluid.Movers.BaseClasses.PartialFlowMachine.

Deprecated model

The model Buildings.Fluid.Movers.FlowMachinePolynomial is in this package for compatibility with older versions of this library. It is recommended to use the other models as they optionally allow use of a medium volume that provides state variables which are needed in some models when the flow rate is zero.

Differences to models in Modelica.Fluid.Machines

The models with names FlowMachine_* have similar parameters than the models in the package Modelica.Fluid.Machines. However, the models in this package differ primarily in the following points:

• They use a different base class, which allows to have zero mass flow rate. The models in Modelica.Fluid restrict the number of revolutions, and hence the flow rate, to be non-zero.
• For the model with prescribed pressure, the input signal is the pressure difference between the two ports, and not the absolute pressure at port_b.
• The pressure calculations are based on total pressure in Pascals instead of the pump head in meters. This change was done to avoid ambiguities in the parameterization if the models are used as a fan with air as the medium. The original formulation in Modelica.Fluid.Machines converts head to pressure using the density medium.d. Therefore, for fans, head would be converted to pressure using the density of air. However, for fans, manufacturers typically publish the head in millimeters water (mmH20). Therefore, to avoid confusion when using these models with media other than water, we changed the models to use total pressure in Pascals instead of head in meters.
• The performance data are interpolated using cubic hermite splines instead of polynomials. These functions are implemented at Buildings.Fluid.Movers.BaseClasses.Characteristics.

Extends from Modelica.Icons.Info (Icon for general information packages).